-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2015; 5(5): 253-258
doi:10.5923/j.ajms.20150505.05

Mathematical Analysis of an HIV/AIDS Epidemic Model
Udoy S. Basak 1, Bimal Kumar Datta 2, Prodip Kumar Ghose 3
1Lecturer, Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh
2Assistant Professor, Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh
3Senior Lecturer, Department of Mathematics, American International University, Bangladesh
Correspondence to: Udoy S. Basak , Lecturer, Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

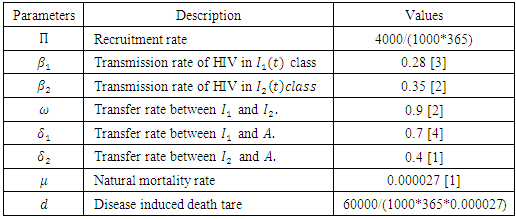
Mathematical model is a very useful tool to understand and analyse the dynamics of diseases. Here we present a non-linear mathematical model which investigates the spread and control of HIV in different populations. Present study fitted the model, which exhibits two equilibrium points namely, the disease free equilibrium and the endemic equilibrium point. The global stability of these equilibrium points is also investigated. The model is analysed by using the basic reproduction number 
Keywords: HIV, AIDS, Basic reproduction number, Endemic equilibrium point, Local and global stability
Cite this paper: Udoy S. Basak , Bimal Kumar Datta , Prodip Kumar Ghose , Mathematical Analysis of an HIV/AIDS Epidemic Model, American Journal of Mathematics and Statistics, Vol. 5 No. 5, 2015, pp. 253-258. doi: 10.5923/j.ajms.20150505.05.
Article Outline
1. Introduction
- HIV is a well known disease throughout the world. According to the World Health Organization (WHO), since the beginning of the epidemic, almost 78 million people have been infected with the HIV virus and about 39 million people have died of HIV. Globally, about 35.0 million people were living with HIV at the end of 2013. An estimated 0.8% of adults aged 15-49 years worldwide are living with HIV, although the burden of the epidemic continues to vary considerably between countries and regions. Sub-Saharan Africa remains most severely affected, with nearly 1 in every 20 adults living with HIV and accounting for nearly 71% of the people living with HIV worldwide. So HIV is one of the greatest threats to the human society. Infection with HIV occurs by the transfer of blood, semen, vaginal fluid, pre-ejaculate or breast milk. Within these body fluids, HIV is present as both free virus particles and virus within infected immune cells [2]. HIV can be transmitted between injecting drug users if the drug equipment (needles, syringes or rinsing water) is contaminated by HIV-infected fluids (usually blood) and is then reused by another person without first sterilizing it. Mother to child transmission of HIV is also possible. According to the UNICEF, nine out of every 10 children under the age of 15 become infected with HIV every year because their mothers are HIV positive. This is known as “mother to child transmission” of HIV. In 2001 alone, 710,000 children under 15 contracted HIV with while in their mother’s womb, during childbirth or through breastfeeding. After entering into the human body, HIV infects vital cells (especially
 T cells), macrophages and dendritic cells. in the human immune system such as helper T cells HIV infection leads to low levels of
T cells), macrophages and dendritic cells. in the human immune system such as helper T cells HIV infection leads to low levels of  T cells through a number of mechanisms including: apoptosis of uninfected by stancer cells, direct viral killing of infected cells, and killing of infected
T cells through a number of mechanisms including: apoptosis of uninfected by stancer cells, direct viral killing of infected cells, and killing of infected 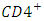 T cells by CD8 cytotoxic lymphocytes that recognize infected cells. When
T cells by CD8 cytotoxic lymphocytes that recognize infected cells. When 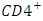 T cell numbers decline below a critical level, cell-mediated immunity is lost, and the body becomes progressively more susceptible to opportunistic infections [1].Without treatment, HIV infection gradually destroys the immune system. Standard HIV treatment (also called antiretroviral therapy or ART) involves taking a combination of HIV medicines from at least two different HIV drugs classes every day. ART is highly effective at preventing HIV from multiplying. Having less HIV in the body protects the immune system and prevents HIV from advancing to AIDS. ART also reduces the risk of HIV drug resistance.
T cell numbers decline below a critical level, cell-mediated immunity is lost, and the body becomes progressively more susceptible to opportunistic infections [1].Without treatment, HIV infection gradually destroys the immune system. Standard HIV treatment (also called antiretroviral therapy or ART) involves taking a combination of HIV medicines from at least two different HIV drugs classes every day. ART is highly effective at preventing HIV from multiplying. Having less HIV in the body protects the immune system and prevents HIV from advancing to AIDS. ART also reduces the risk of HIV drug resistance. 2. Formulation of the Model
- The total sexually-active population at time t, is denoted by
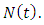 This population
This population 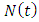 is divided into four mutually-exclusive compartments, namely susceptible class S(t), the infected individuals who do not know that they are infected
is divided into four mutually-exclusive compartments, namely susceptible class S(t), the infected individuals who do not know that they are infected 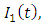 the infected individuals who do know that they are infected
the infected individuals who do know that they are infected 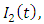 and that of the AIDS populations
and that of the AIDS populations 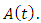 Hence the total population at time t,
Hence the total population at time t, 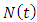 can be written as
can be written as 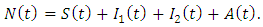 It is assumed that individuals are recruited at a constant rate Π to the susceptible class S(t). Susceptible individuals can be infected with HIV following the contact with infected individuals at a rate λ, where
It is assumed that individuals are recruited at a constant rate Π to the susceptible class S(t). Susceptible individuals can be infected with HIV following the contact with infected individuals at a rate λ, where 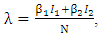 where
where 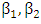 are the transmission rates for HIV. The individuals in the
are the transmission rates for HIV. The individuals in the 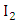 class are more infectious than those in the
class are more infectious than those in the 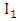 class. Therefore we must have
class. Therefore we must have 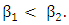 Suppose that the individuals of the
Suppose that the individuals of the 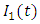 class enter into the
class enter into the 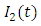 class at a rate
class at a rate 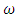 and into the AIDS class
and into the AIDS class 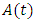 at a rate
at a rate  Again suppose that the individuals of the
Again suppose that the individuals of the 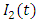 class progress into the AIDS class at a rate
class progress into the AIDS class at a rate 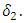 Let
Let 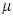 and
and 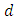 denote the natural mortality rate and disease induced death rate respectively. Under the above considerations, the model dynamics is assumed to be governed by the following system of ordinary differential equations
denote the natural mortality rate and disease induced death rate respectively. Under the above considerations, the model dynamics is assumed to be governed by the following system of ordinary differential equations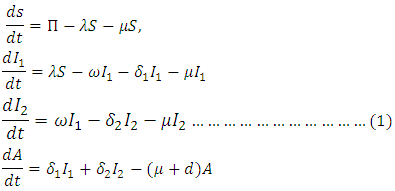
3. Analysis of the Model
3.1. Invariant Region
- All the parameters of the model are assumed to be non-negative. On the other hand, model (1) monitors human population, so the state variables are non-negative for all time
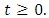 Total population can be written as
Total population can be written as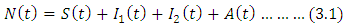 Here Eq. (2) is changing at a rate
Here Eq. (2) is changing at a rate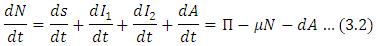 In the absence of disease i.e. for
In the absence of disease i.e. for 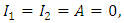 we have
we have By the separation of variables of differential inequality (3.3) we must have
By the separation of variables of differential inequality (3.3) we must have 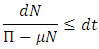 Integrating the above equation we have
Integrating the above equation we have 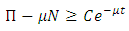 where
where 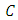 is a constant which is to be determined. Let at
is a constant which is to be determined. Let at 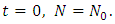 So we have,
So we have, 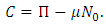 From Eq. (3.4) we have
From Eq. (3.4) we have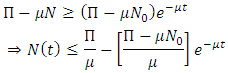 As
As 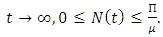 Therefore, the feasible solutions set of the system (1) enters the region:
Therefore, the feasible solutions set of the system (1) enters the region: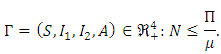 In this case, whenever
In this case, whenever 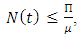 every solution with initial condition in
every solution with initial condition in 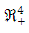 remains in that region for
remains in that region for 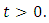 Thus the model is well posed and epidemiologically meaningful in the domain
Thus the model is well posed and epidemiologically meaningful in the domain 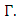
3.2. Positivity of Solutions
- In this section, we discuss the positivity of the solutions which describes the non-negativity of the solutions of the system (1). Let the initial data be
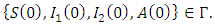 Then we need to show that the solution set
Then we need to show that the solution set 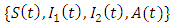 of system (1) is positive for
of system (1) is positive for 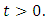 From the first equation of the system (1) we have
From the first equation of the system (1) we have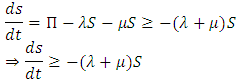 Integrating we have s
Integrating we have s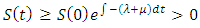 provided
provided 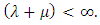 Similarly from the 2nd, 3rd and 4th equation of model (1) we have:
Similarly from the 2nd, 3rd and 4th equation of model (1) we have: Thus the solution set
Thus the solution set 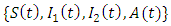 of system (1) is positive for all
of system (1) is positive for all 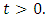
4. Disease-Free Equilibrium Point
- Disease-free equilibrium (DFE) points of a disease model are its steady-state solutions in the absence of infection or disease. We denote the DFE point by
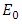 and define the “diseased” classes that are either exposed or infectious. For all equilibrium points we have
and define the “diseased” classes that are either exposed or infectious. For all equilibrium points we have 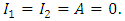 The positive disease-free equilibrium point for the model (1) is
The positive disease-free equilibrium point for the model (1) is 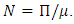 The model (1) has exactly one disease-free equilibrium point and the equilibrium point is
The model (1) has exactly one disease-free equilibrium point and the equilibrium point is 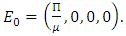 We need to show that the DFE is the only equilibrium point of the model (1). Substituting
We need to show that the DFE is the only equilibrium point of the model (1). Substituting 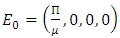 in the model (1) shows all derivatives equal to zero; hence DFE is an equilibrium point. From the above lemma, the only equilibrium point for
in the model (1) shows all derivatives equal to zero; hence DFE is an equilibrium point. From the above lemma, the only equilibrium point for 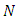 is
is 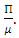 Thus the only equilibrium point for the model (1) is DFE [3].
Thus the only equilibrium point for the model (1) is DFE [3].5. Local Stability of DFE Point
- The local stability of the model (1) is highly dependent on the basic reproduction number which is denoted by
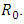 The associated non-negative matrix
The associated non-negative matrix 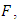 for the new infection terms and the non-singular M-matrix,
for the new infection terms and the non-singular M-matrix, 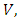 for the remaining transfer terms, are given, respectively by
for the remaining transfer terms, are given, respectively by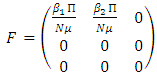 and
and 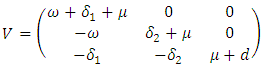 The basic reproduction number
The basic reproduction number 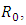 is the spectral radius of the matrix
is the spectral radius of the matrix 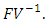 The Eigenvalues of the matrix
The Eigenvalues of the matrix 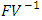 are
are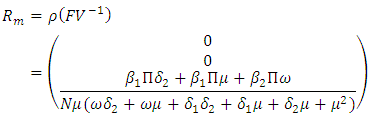 So the basic reproduction number is
So the basic reproduction number is 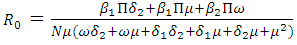 The disease-free equilibrium point
The disease-free equilibrium point 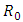 of the model (1) is locally asymptotically stable if
of the model (1) is locally asymptotically stable if 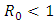 and unstable if
and unstable if 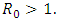
6. Global Stability of DFE Point
- The global asymptotically (GAS) of the disease-free state of the model is investigated using the theorem by Castillo-Chavez [1]. So from the model (1) we have:
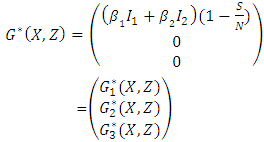 Since
Since 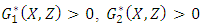 and
and 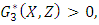 so the condition is satisfied. So
so the condition is satisfied. So 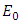 is globally asymptotically stable when
is globally asymptotically stable when 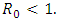
7. Endemic Equilibrium of the Model
- The endemic equilibrium of the model is studied by using the Central Manifold Theorem [1]. To apply this theorem we need to change the variables as follows:
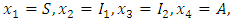 so that
so that 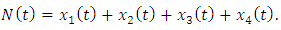 Then the model (1) can be written in the form
Then the model (1) can be written in the form 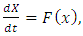 where
where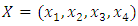 and
and 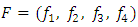 as
as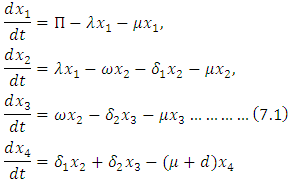 where
where 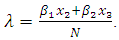 The Jacobian of the system (7.1) is
The Jacobian of the system (7.1) is 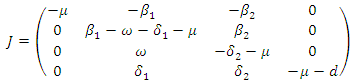 To analyse the dynamics of (7.1), we compute the Eigen values of the Jacobian of (7.1) at the disease free equilibrium point. It can be shown that this Jacobian has a right eigenvector given by:
To analyse the dynamics of (7.1), we compute the Eigen values of the Jacobian of (7.1) at the disease free equilibrium point. It can be shown that this Jacobian has a right eigenvector given by: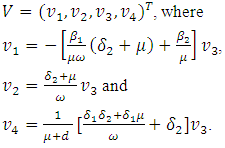 The left eigenvectors are given by
The left eigenvectors are given by 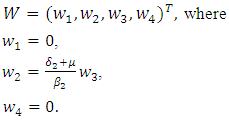 Now using (7.1) we have
Now using (7.1) we have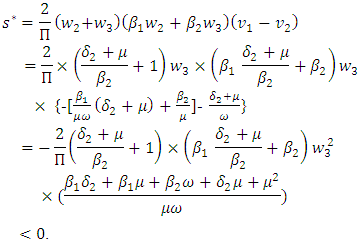 and
and 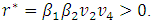 Thus the model (7.1) satisfies the required criteria. So the model (1) has a unique endemic equilibrium point which is locally asymptotically stable when
Thus the model (7.1) satisfies the required criteria. So the model (1) has a unique endemic equilibrium point which is locally asymptotically stable when 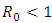 and unstable when
and unstable when 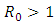 [4].
[4].
|
|
8. Numerical Simulation and Discussions
- Here
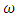 is the transmission rate of HIV from
is the transmission rate of HIV from 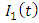 to
to 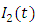 class. The effect of
class. The effect of 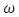 is monitored in the figure (1) and (2). From the figure it is observed that if we increase the value of
is monitored in the figure (1) and (2). From the figure it is observed that if we increase the value of 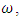 then the value of
then the value of 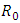 decreases. Hence the number of infected population also decreases.
decreases. Hence the number of infected population also decreases.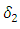 is the transmission of the disease from
is the transmission of the disease from 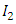 class to the AIDS class
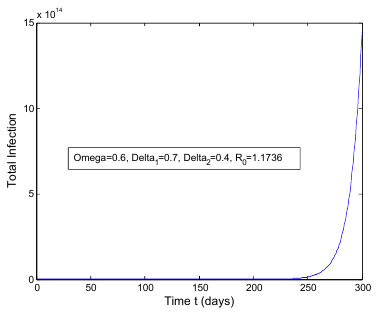
class to the AIDS class 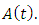 In the figure (3) and (4), the effect of
In the figure (3) and (4), the effect of 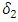 is observed. The increment in the value of
is observed. The increment in the value of 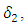 increases the basic reproduction number
increases the basic reproduction number 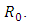 As a result it increases the number of total infected population. The prevalence of the disease is being monitored in the figure (5) and (6).In this paper, a non-linear mathematical model is formulated. Sufficient conditions are given ensuring the local and global stability of the disease free equilibrium point and unique endemic equilibrium point. The disease free equilibrium point
As a result it increases the number of total infected population. The prevalence of the disease is being monitored in the figure (5) and (6).In this paper, a non-linear mathematical model is formulated. Sufficient conditions are given ensuring the local and global stability of the disease free equilibrium point and unique endemic equilibrium point. The disease free equilibrium point 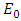 is shown locally asymptotically stable when the basic reproduction number
is shown locally asymptotically stable when the basic reproduction number 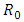 is less than unity. The global stability is also investigated. Finally we have shown that the model has a unique endemic equilibrium point which is locally asymptotically stable.
is less than unity. The global stability is also investigated. Finally we have shown that the model has a unique endemic equilibrium point which is locally asymptotically stable.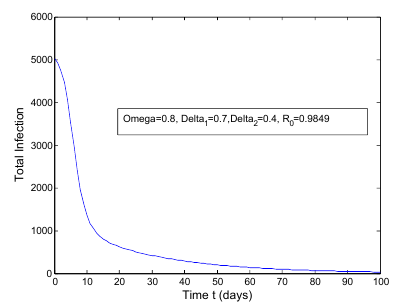 | Figure 1. Total infection as a function of time for model (1) with different values of 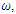 where where 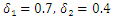 |
 | Figure 2. Total infection as a function of time for model (1) with different values of 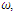 where where 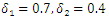 |
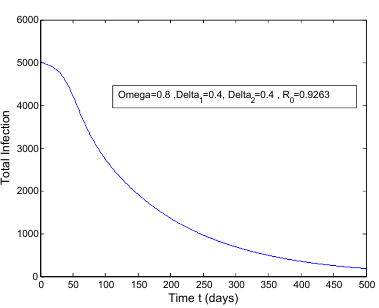 | Figure 3. Total infection as a function of time for model (1) with different values of 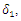 where where 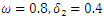 |
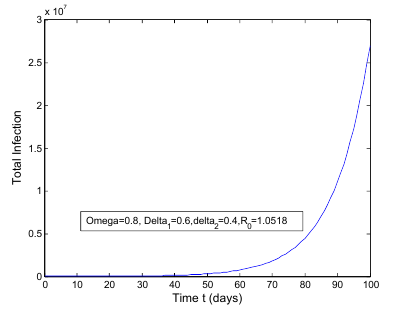 | Figure 4. Total infection as a function of time for model (1) with different values of 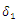 |
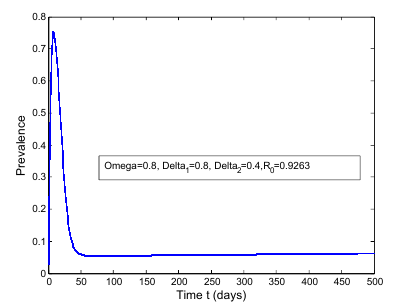 | Figure 5. Prevalence as a function of time for model (1) with different values of 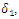 where where 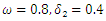 |
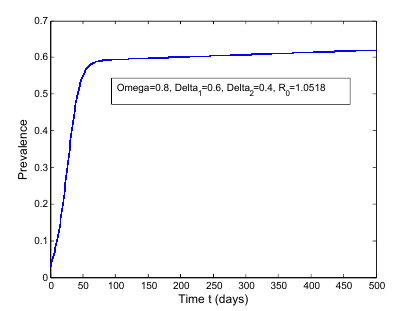 | Figure 6. Prevalence as a function of time for model (1) with different values of 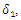 where where 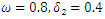 |
9. Conclusions
- In summary, the main findings of the paper are given below:• We can control the disease burden by controlling the effective contact rate of the infected population. • Controlling the transfer rate
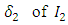 class to the AIDS class
class to the AIDS class 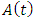 the disease elimination if feasible. • The most effective way to lower the incidence rate is to isolate the susceptible population as soon as possible.
the disease elimination if feasible. • The most effective way to lower the incidence rate is to isolate the susceptible population as soon as possible. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML