-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2015; 5(4): 200-219
doi:10.5923/j.ajms.20150504.06
Existence and Uniqueness of the Mild Solution to the Fractional Order Impulsive Nonlinear Control System
Sameer Qasim Hasan, Fawzi Mutter Ismaeel
Al-Mustansrea University, College of Education, Mathematics Department
Correspondence to: Sameer Qasim Hasan, Al-Mustansrea University, College of Education, Mathematics Department.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The present paper investigates the existence of mild solutions for some impulsive multi-fractional order control systems with nonlocal initial value conditions and neutral delay. The existence results are obtained by the fixed point theorem. The uniqueness of the mild solution is further discussed in the absence of the delay.
Keywords: Impulsive nonlinear control system
Cite this paper: Sameer Qasim Hasan, Fawzi Mutter Ismaeel, Existence and Uniqueness of the Mild Solution to the Fractional Order Impulsive Nonlinear Control System, American Journal of Mathematics and Statistics, Vol. 5 No. 4, 2015, pp. 200-219. doi: 10.5923/j.ajms.20150504.06.
Article Outline
1. Introduction
- In this paper we studied some new classes of impulsive multi-integro fractional order and multi-fractional order with Caputo and Riemann level derivative respectively and nonlocal conditions and natural infinite delay.We consider the new classes of impulsive multi fractional order differential nonlinear equations with nonlocal conditions and natural infinite delay with cosin semigroup generated by unbounded linear operator and uniformly bounded as well as its derivative and presented some properties of the Riemann-Leovel derivatives and integration that need in proving of locally existence and a new definition of
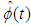 function. The necessary and sufficient conditions of existence have been presented and given in details. The uniqueness solution of this classes have been presented without delay with some necessary conditions. The results in [6], [15], [21], [20], was developed with this classes in system (3.1) with multi-fractional derivatives which defined on
function. The necessary and sufficient conditions of existence have been presented and given in details. The uniqueness solution of this classes have been presented without delay with some necessary conditions. The results in [6], [15], [21], [20], was developed with this classes in system (3.1) with multi-fractional derivatives which defined on 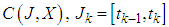 ,
, 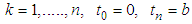 all above result have been given the mild solution in piecewise continuous space
all above result have been given the mild solution in piecewise continuous space 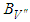 .The existence conditions for the fractional order impulsive integro-differential non-quasilinear equations with neutral infinite delay and nonlocal integral condition have been considered and developed of the works in [11], [8], [12], [5], [10], [13], [3], [4], [18], [17], [2]. The class of equations considered in the paper constitutes an important subclass of control systems since such models appear as a natural description of several real processes, and extend many classical initial value problems. The paper studies the existence-uniqueness of the mild solution, which constitutes a crucial step in the study of any control problem.
.The existence conditions for the fractional order impulsive integro-differential non-quasilinear equations with neutral infinite delay and nonlocal integral condition have been considered and developed of the works in [11], [8], [12], [5], [10], [13], [3], [4], [18], [17], [2]. The class of equations considered in the paper constitutes an important subclass of control systems since such models appear as a natural description of several real processes, and extend many classical initial value problems. The paper studies the existence-uniqueness of the mild solution, which constitutes a crucial step in the study of any control problem.2. Preliminaries
- Let X and U be a pair of real Banach spaces, with norms
 and
and 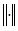 , respectively. Which is use it in next section consider the existance of the fractional impulsive mixed-type integro-differential partial functional equation with neutral infinite delay and nonlocal conditions.Definition (1.2), [18]:The piecewise continuous space which defined on a Banach space X is denoted by
, respectively. Which is use it in next section consider the existance of the fractional impulsive mixed-type integro-differential partial functional equation with neutral infinite delay and nonlocal conditions.Definition (1.2), [18]:The piecewise continuous space which defined on a Banach space X is denoted by 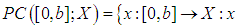 is continuous at
is continuous at 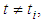 left continuous at
left continuous at 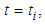 and the right-hand limit
and the right-hand limit 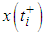 exists for
exists for 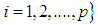 .Note that the
.Note that the 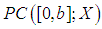 equipped with the norm
equipped with the norm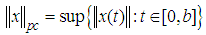 is a Banach space.Definition (2.2) "Compact Operator", [25]:Let X and Y be normed spaces, the operator
is a Banach space.Definition (2.2) "Compact Operator", [25]:Let X and Y be normed spaces, the operator 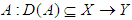 is called a compact if:1. A is continuous, and2. A transforms bounded subset M of X into relatively compact subset in
is called a compact if:1. A is continuous, and2. A transforms bounded subset M of X into relatively compact subset in 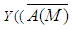 is compact).Definitions (2.3), [24]:A subset U of
is compact).Definitions (2.3), [24]:A subset U of 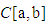 is said to be equicontinuous if for each
is said to be equicontinuous if for each 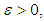 there is a
there is a 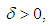 such that:
such that: 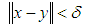 and
and 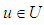 , imply
, imply 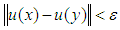 .Lemma (2.1), "Completely Continuous Operator", [19]:Let X be a normed space, the mapping
.Lemma (2.1), "Completely Continuous Operator", [19]:Let X be a normed space, the mapping 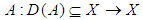 is called completely continuous if it is compact.Remark (2.1), [9]:Compact operator on Banach space are always completely continuous.Definition (2.4), [16]:Let X be a metric space equipped with a distance d. A map
is called completely continuous if it is compact.Remark (2.1), [9]:Compact operator on Banach space are always completely continuous.Definition (2.4), [16]:Let X be a metric space equipped with a distance d. A map 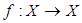 is said to be Lipschitz continuous if there is
is said to be Lipschitz continuous if there is 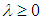 such that
such that 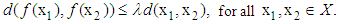 The smallest
The smallest 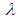 for which the inequality holds is the Lipschitz constant of f. If
for which the inequality holds is the Lipschitz constant of f. If 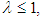 f is said to be nonexpansive, if
f is said to be nonexpansive, if 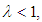 f is said to be a contraction.Theorem (2.1) "Arezola-Ascoli's theorem", [19]:Let
f is said to be a contraction.Theorem (2.1) "Arezola-Ascoli's theorem", [19]:Let 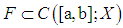 satisfy:i. For any
satisfy:i. For any 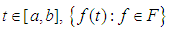 is relatively compact on X.ii.
is relatively compact on X.ii. 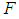 is equicontinuous on
is equicontinuous on 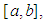 that is, for any
that is, for any 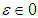 and any
and any 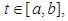 there exists
there exists 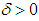 such that:
such that: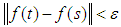 for any
for any 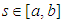 satisfying
satisfying 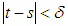 and all
and all 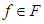 .Then is a relatively compact.Theorem (2.2) "Schauder's Fixed-Point theorem", [19]:Let
.Then is a relatively compact.Theorem (2.2) "Schauder's Fixed-Point theorem", [19]:Let 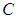 be a nonempty bounded convex closed subset in
be a nonempty bounded convex closed subset in 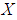 if
if  is continuous and
is continuous and 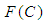 is relatively compact, then
is relatively compact, then 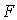 has at least one fixed point. Theorem (2.3) "Leray-Schauder Principle", [25]:Suppose
has at least one fixed point. Theorem (2.3) "Leray-Schauder Principle", [25]:Suppose 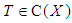 and any solution of
and any solution of 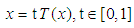 satisfies the priori bound
satisfies the priori bound 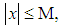 for
for 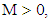 then T has a fixed point.Definition (2.5) "Strongly Continuous Semigroup", [7]:A semigroup
then T has a fixed point.Definition (2.5) "Strongly Continuous Semigroup", [7]:A semigroup 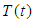 ,
, 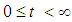 of bounded linear operators on a Banach space X is a
of bounded linear operators on a Banach space X is a 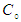 -semigroup of bounded linear operators if:
-semigroup of bounded linear operators if: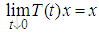 , for every
, for every 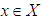 .Definition(2.6), [14]:If
.Definition(2.6), [14]:If 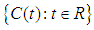 is a strongly continuous cosine family in X, i.
is a strongly continuous cosine family in X, i. 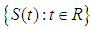 associated to the given strongly continuous cosine family, is defined by
associated to the given strongly continuous cosine family, is defined by 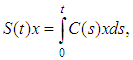
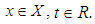 ii. The infinitesimal generator
ii. The infinitesimal generator 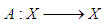 of a cosine family
of a cosine family 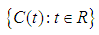 is defined by
is defined by 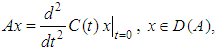 where
where 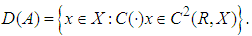 Remark (2.2), [22]:Let
Remark (2.2), [22]:Let 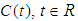 cosine family of bounded linear operators. Then
cosine family of bounded linear operators. Then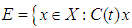 is once continuously differentiable in
is once continuously differentiable in 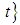 .Lemma (2.2), [22]:Let A be a generator of strongly continuous cosine family
.Lemma (2.2), [22]:Let A be a generator of strongly continuous cosine family 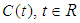 of bounded linear operators. Then
of bounded linear operators. Then 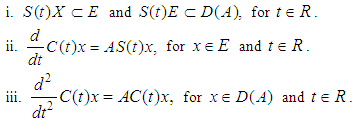 Definition (2.7) "mild solution", [23]:Let A be infinitesimal generator of a Co-semigroup T(t). Let
Definition (2.7) "mild solution", [23]:Let A be infinitesimal generator of a Co-semigroup T(t). Let 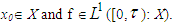 The function
The function 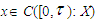 given by:
given by: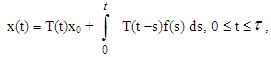 is the mild solution of the above non homgenous initial value problem.Definition (2.8), [1]:The Riemann-Liouvill fractional derivative of order
is the mild solution of the above non homgenous initial value problem.Definition (2.8), [1]:The Riemann-Liouvill fractional derivative of order 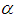 for a function
for a function 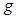 is defined by
is defined by 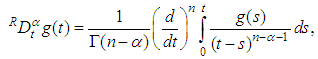
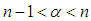 , provided the right hand side is pointwise defined on
, provided the right hand side is pointwise defined on 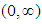 .Definition (2.9), [1]: The Riemann-Liouvill fractional integral of order
.Definition (2.9), [1]: The Riemann-Liouvill fractional integral of order 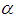 for a function
for a function 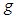 is defined as
is defined as 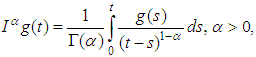 provided the right hand side is pointwise defined on
provided the right hand side is pointwise defined on 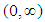 .Lemma (2.3), [20]:If
.Lemma (2.3), [20]:If 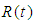 is a linear operator such that
is a linear operator such that 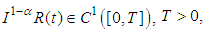 then, for
then, for 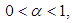 we have
we have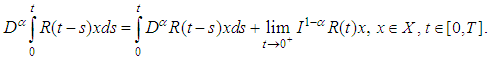 Lemma (2.4), [20]:If
Lemma (2.4), [20]:If 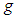 is a continuous function such that
is a continuous function such that 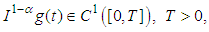 and
and 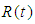 is continuous, then, for
is continuous, then, for 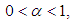 we have
we have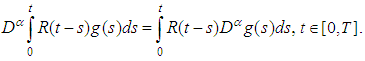 Corollary (2.1), [20]:For the sine family
Corollary (2.1), [20]:For the sine family 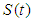 associated with the cosine family
associated with the cosine family 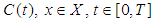 and
and 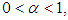 we have
we have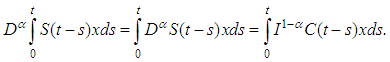 Hypotheses (2.1):The following hypotheses of
Hypotheses (2.1):The following hypotheses of 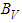 constriction needed in description of piecewise continuous space
constriction needed in description of piecewise continuous space 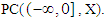 . 1.
. 1. 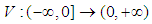 is a continuous function satisfy
is a continuous function satisfy 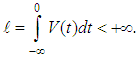 The Banach space
The Banach space 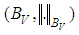 induced by the function
induced by the function 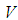 is defined as follows
is defined as follows 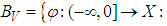 for any
for any 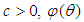 is a bounded and measurable function on
is a bounded and measurable function on 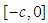 and
and 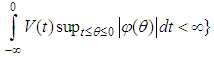 endowed with the norm
endowed with the norm 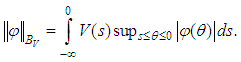 2. Let
2. Let 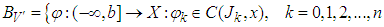 and there exist
and there exist  and
and 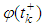 with
with 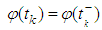 ,
, 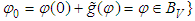 where
where 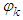 is the restriction of
is the restriction of 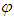 to
to 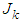 ,
, 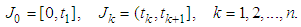 Denote by
Denote by 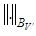 a seminorm in space
a seminorm in space 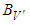 as follows
as follows 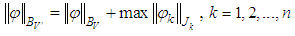 where
where 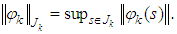
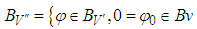 with norm
with norm 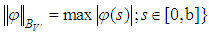 .
. 3. Existence of a Multi-Fractional Order Impulsive Nonlinear Control System Via Cosine Semigroup
- Consider the following multi-fractional order impulsive control system with nonlocal initial value conditions.
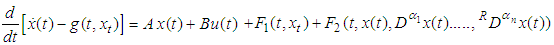
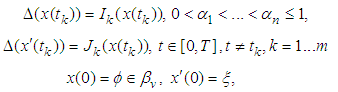 | (3.1) |
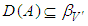 where
where 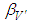 defined in hypotheses (2.1).
defined in hypotheses (2.1). 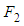 is a nonlinear function from
is a nonlinear function from 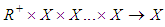 , the control function u(.) lies in a Banach space
, the control function u(.) lies in a Banach space 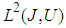 of admissible control functions. B is a bounded linear from a Banach space U into X,
of admissible control functions. B is a bounded linear from a Banach space U into X, 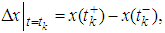 for all
for all 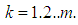
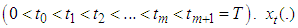 which defined as
which defined as 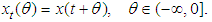 We shall make the following hypotheses:1.
We shall make the following hypotheses:1. 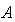 is the infinitesimal generator of a strongly continuous cosine family
is the infinitesimal generator of a strongly continuous cosine family 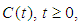 of bounded linear operator in the Banach space
of bounded linear operator in the Banach space 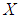 . The associated sine family
. The associated sine family 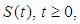 is defined in definition (2.6).2.
is defined in definition (2.6).2. 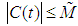 and
and 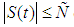 on
on 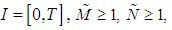 depend on
depend on 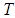 .To define and find the mild solution of problem (3.1), let by condition (1), C(t),
.To define and find the mild solution of problem (3.1), let by condition (1), C(t), 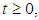 is a strongly cosine semigroup generated by the linear operator A, and let x(t) be the solution of (3.1). Then by Remark (2.2) we have C(t)x is differentiable that implies
is a strongly cosine semigroup generated by the linear operator A, and let x(t) be the solution of (3.1). Then by Remark (2.2) we have C(t)x is differentiable that implies 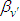 -valued function
-valued function 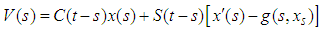 is differentiable for
is differentiable for 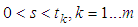 and:
and: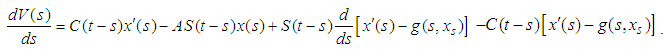 Take the integration from 0 to t of both sides and shchas the technique that are using to find the mild in theorem (3.4), we used in the following:
Take the integration from 0 to t of both sides and shchas the technique that are using to find the mild in theorem (3.4), we used in the following: 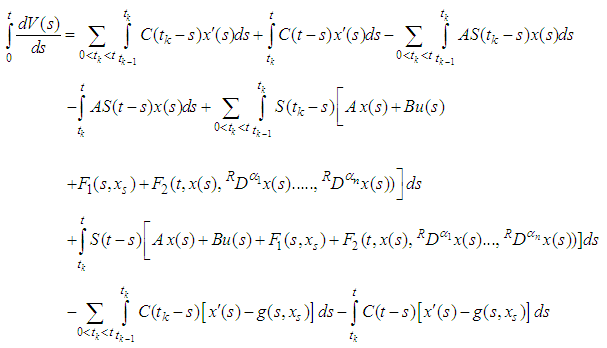 Hence,
Hence,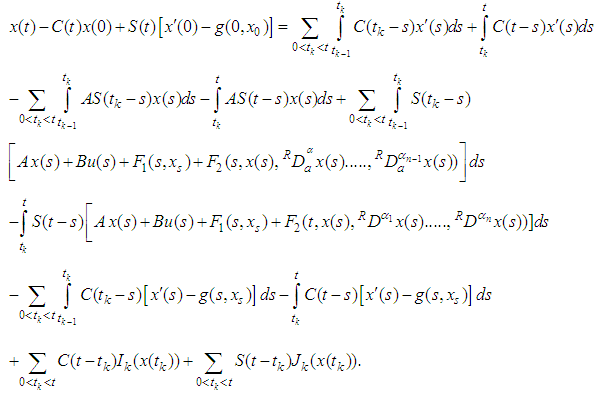 Therefore,
Therefore,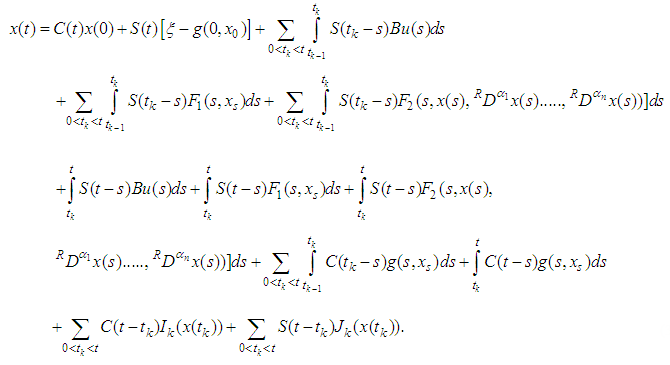 | (3.2) |
 is called a mild solution of the problem (3.1) if
is called a mild solution of the problem (3.1) if  , the impulsive conditions
, the impulsive conditions 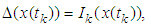
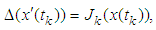
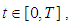 ,
, is verified, the restriction of
is verified, the restriction of 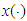 to the interval
to the interval 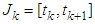 is continuous and the following integral equation holds for
is continuous and the following integral equation holds for 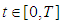 .
.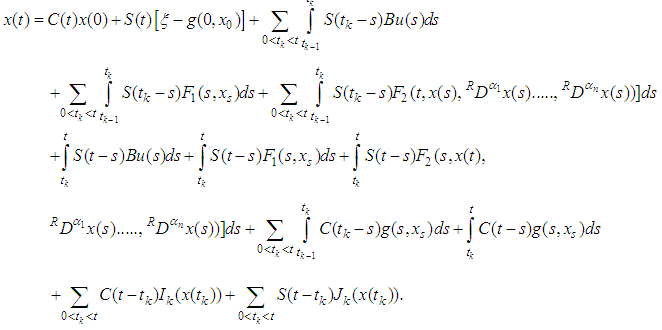 | (3.3) |
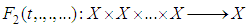 is uniformly continuous for a.e
is uniformly continuous for a.e 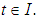 For every
For every 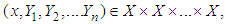 the function is strongly measurable.ii. There exists a nonnegative continuous function
the function is strongly measurable.ii. There exists a nonnegative continuous function 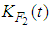 and a continuous nondecreasing positive function
and a continuous nondecreasing positive function 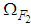 such that:
such that: 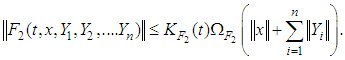 iii. For each
iii. For each 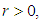 the set
the set 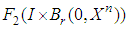 is relatively compact in
is relatively compact in 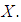 4. i.
4. i. 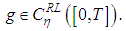 ii. There exist a nonnegative continuous function
ii. There exist a nonnegative continuous function 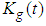 and continuous nondecreasing positive function
and continuous nondecreasing positive function 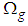 such that
such that 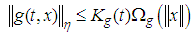 , for
, for 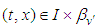 .iii. The family of functions
.iii. The family of functions 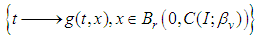 is equicontinuous on
is equicontinuous on 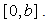 iv. For each
iv. For each 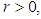 the set
the set 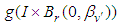 is relatively compact in
is relatively compact in 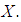 5.
5. 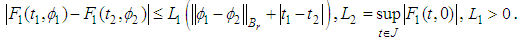 6.
6. 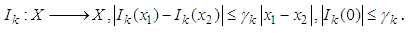
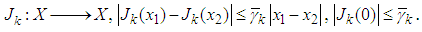
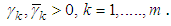 7. The linear operator B satisfies the following
7. The linear operator B satisfies the following 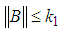 ,
, 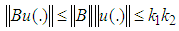 , for positive constant
, for positive constant 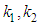 .8. Let
.8. Let 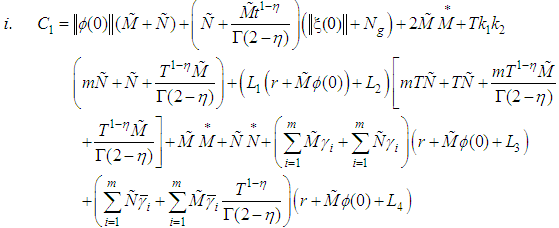
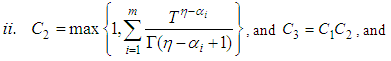
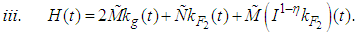 Remark (3.3):From conditions (3) (iii) and (4) (ii) above, we have the following:(a)
Remark (3.3):From conditions (3) (iii) and (4) (ii) above, we have the following:(a) 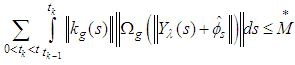 , where
, where 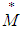 is positive constant.(b)
is positive constant.(b) 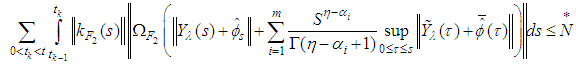 , where
, where  is positive constant.Remark (3.4):We need the following inequalities for complete the prove of existence theorem.
is positive constant.Remark (3.4):We need the following inequalities for complete the prove of existence theorem. 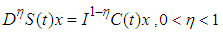 , thus
, thus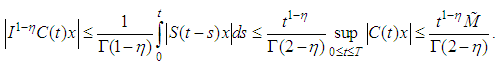 We define
We define 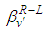 as follows:
as follows: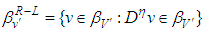 | (3.4) |
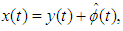 and for
and for 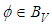 , we define
, we define 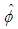 function by
function by 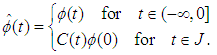 Theorem (3.4):Assume the Hypotheses (1-7) and
Theorem (3.4):Assume the Hypotheses (1-7) and 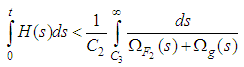 | (3.5) |
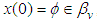 ,
, 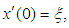 the Multi-fractional order impulsive nonlocal initial value control problem (3.1) has a mild solution
the Multi-fractional order impulsive nonlocal initial value control problem (3.1) has a mild solution 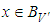 for every control
for every control 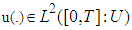 Proof: From definition(3.10) and for
Proof: From definition(3.10) and for 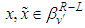 the maps define as:
the maps define as: 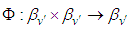
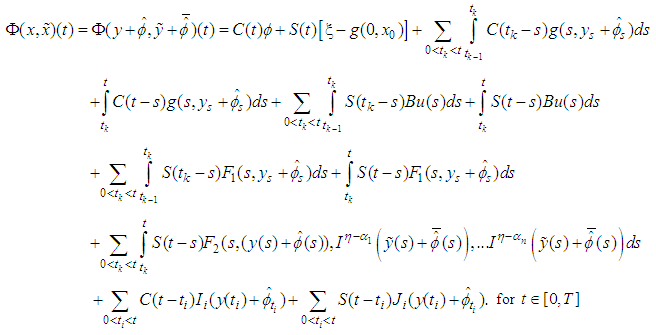 | (3.6) |
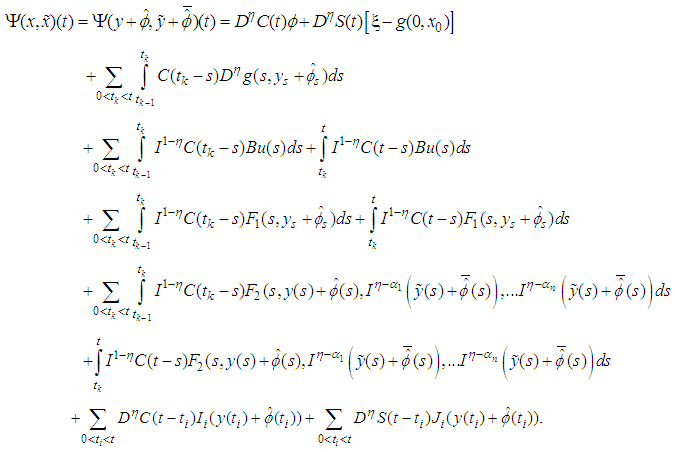 | (3.7) |
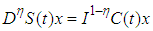 and
and 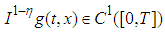 , and from lemma(2.3), we get
, and from lemma(2.3), we get 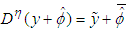 .To satisfies theorem (2.2) for finding a fixed point need to do the following:
.To satisfies theorem (2.2) for finding a fixed point need to do the following: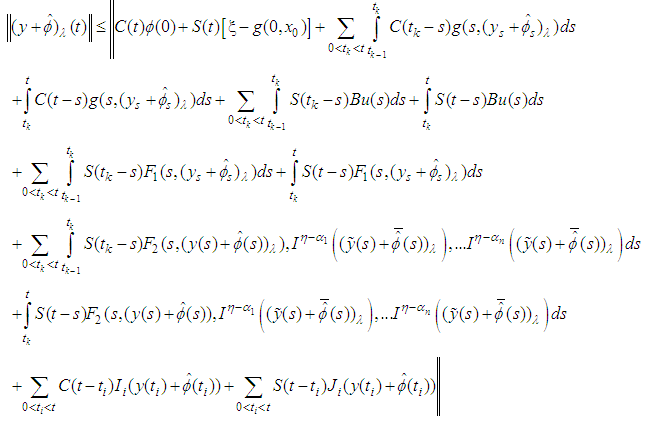 | (3.8) |
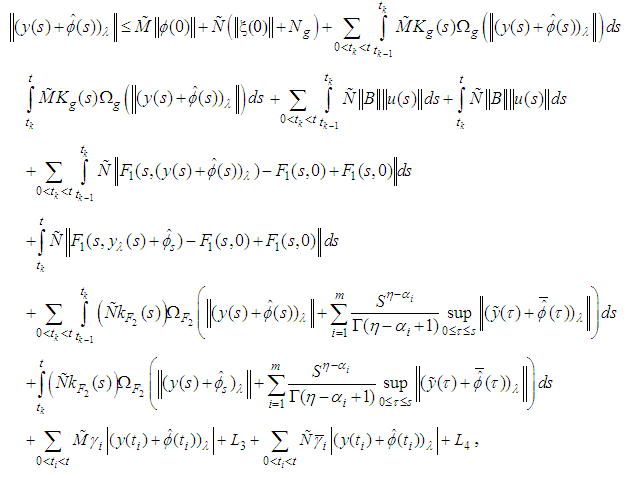 thus
thus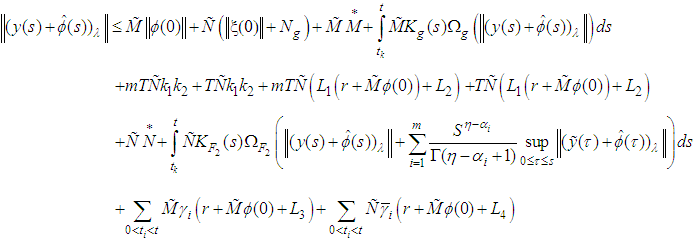 Also, from equation (3.7), we obtain:
Also, from equation (3.7), we obtain: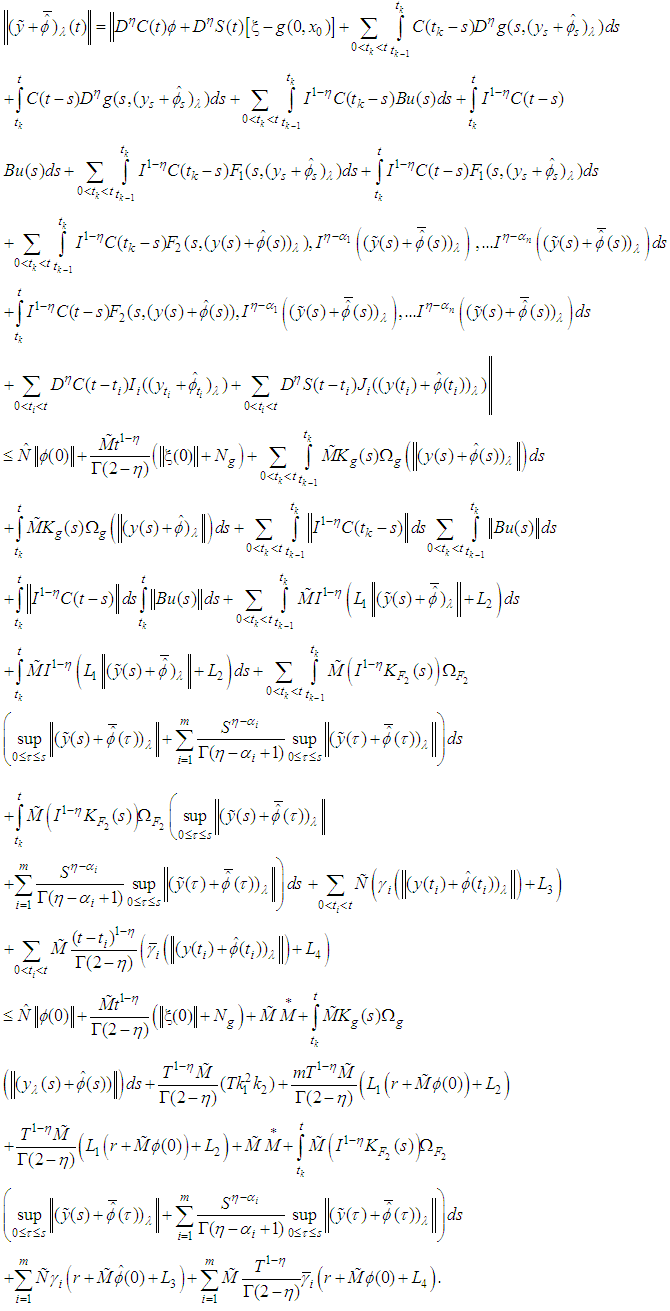 From condition (8)(i), we have that
From condition (8)(i), we have that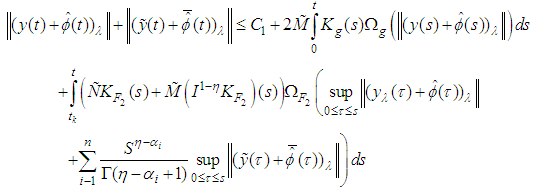 | (3.9) |
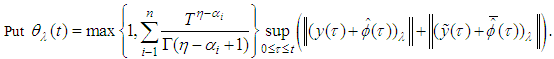
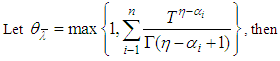
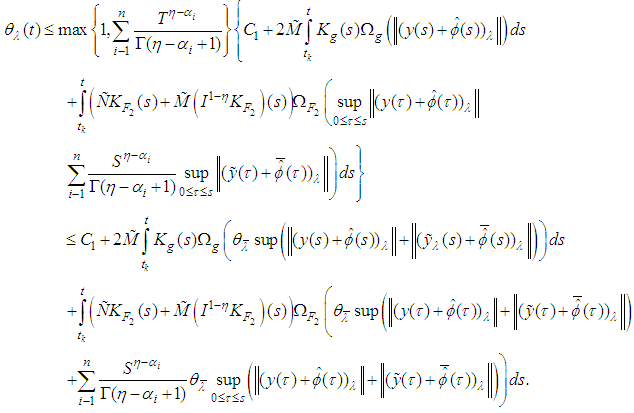
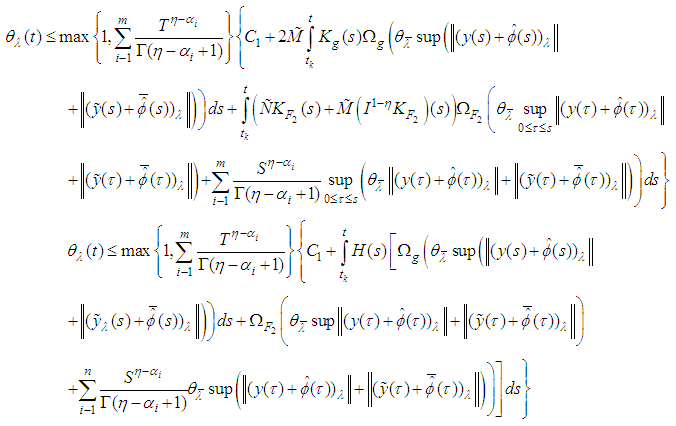 From condition (8), (ii), (iii), we get
From condition (8), (ii), (iii), we get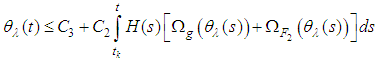 | (3.10) |
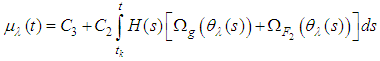 Then
Then 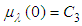 and
and 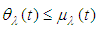
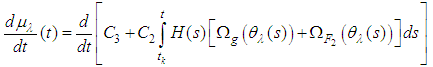
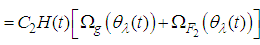 , thus
, thus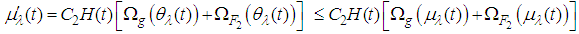 , therefore
, therefore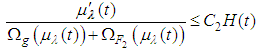 , By taking the integral in both sides we get:
, By taking the integral in both sides we get: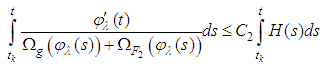 let
let 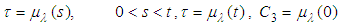 ,
,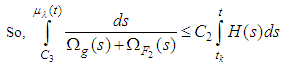 | (3.11) |
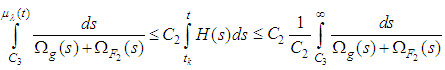
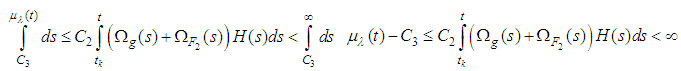 Hence
Hence 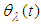 is bounded and then
is bounded and then 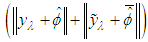 is bounded.Thus the set of solution of (3.8) is bounded in
is bounded.Thus the set of solution of (3.8) is bounded in 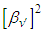 . To prove that
. To prove that 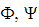 are completely continuous, from the mild solution (3.2), we get
are completely continuous, from the mild solution (3.2), we get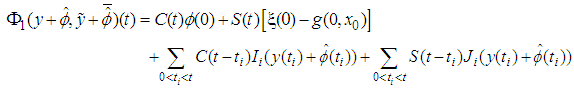 Since
Since 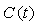 and
and 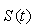 are bounded on [0,T] and closed, then are compact.and also
are bounded on [0,T] and closed, then are compact.and also 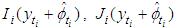 are bounded, then the multiplication of bounded and compact set is compact, hence compact on Banach Space is completely continuous (see lemma(2.1)). Now:
are bounded, then the multiplication of bounded and compact set is compact, hence compact on Banach Space is completely continuous (see lemma(2.1)). Now: 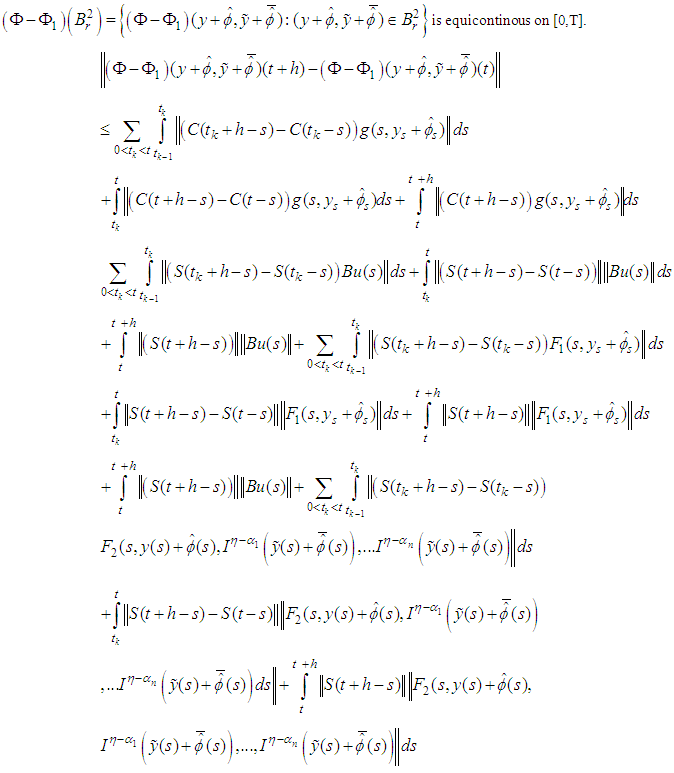 By (1) and (4), for
By (1) and (4), for  and
and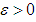 , there exists
, there exists 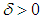 such that:
such that: 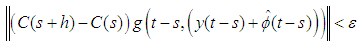 for
for 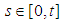 and
and 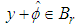 where
where 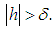 This together with (3), (4) and the fact that
This together with (3), (4) and the fact that 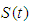 satisfies Lipschitz condition, imply that:
satisfies Lipschitz condition, imply that: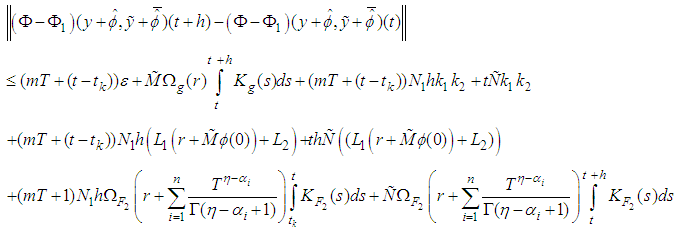 Thus
Thus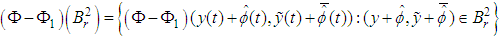 is equicontinuous on
is equicontinuous on  By
By 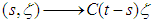 is continuous from
is continuous from 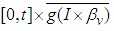 to
to 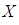 and from (4) (iv) that
and from (4) (iv) that 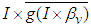 is relative compact in
is relative compact in 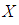 .The set
.The set 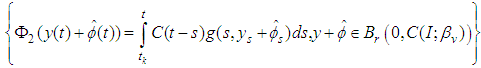 .Since
.Since 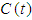 is continuous and defined on relative compact set
is continuous and defined on relative compact set 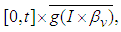 then the above set is relative compact in
then the above set is relative compact in 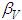 By remark (2.1), we get
By remark (2.1), we get 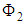 is completely continuous. Let
is completely continuous. Let 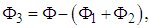 thus
thus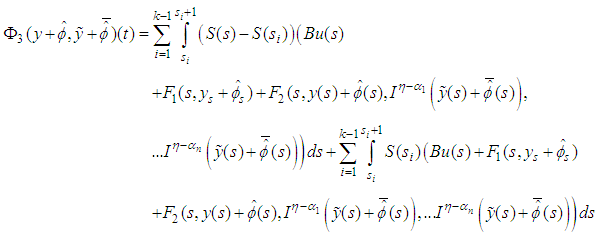 and select the partition
and select the partition 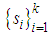 of
of 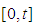 for
for 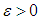
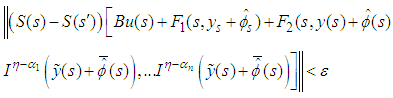 For
For 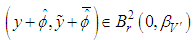 then
then 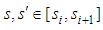 for
for 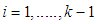 Since
Since 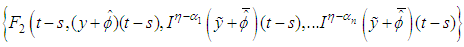 is bounded from (3), (iii) and
is bounded from (3), (iii) and 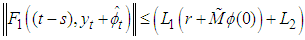 also
also  is uniformly Lipschitz on
is uniformly Lipschitz on 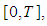 we obtain
we obtain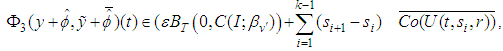 where
where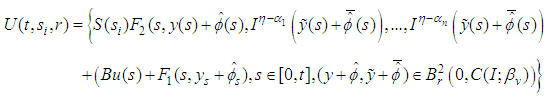 Therefore
Therefore 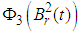 is relative compact in
is relative compact in 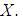 By theorem (2.1), we have that
By theorem (2.1), we have that 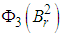 is relatively compact in
is relatively compact in 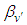 then
then 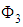 is completely continuous (see lemma (2.1)). Similarly we can prove that
is completely continuous (see lemma (2.1)). Similarly we can prove that 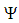 is completely continuous. Hence
is completely continuous. Hence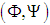 has a fixed point in
has a fixed point in 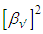 .
. 3.1. Uniqueness of the Multi-Fractional Order impulsive Differential Nonlinear control System via Cosine Semigroup
- In this part, the Uniqueness of the solution to the system (3.1) without Neutral infinite delay has been developed on.
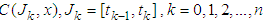 Via cosine semigroup operators.Theorem (3.5):Assume the hypotheses (1-3), (4)(i), (5)(i), (7) and i.
Via cosine semigroup operators.Theorem (3.5):Assume the hypotheses (1-3), (4)(i), (5)(i), (7) and i. 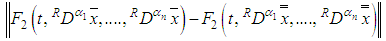
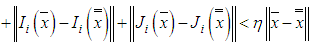 andii.
andii. 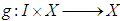 satisfies Lipschitz condition such that
satisfies Lipschitz condition such that 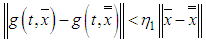 iii.
iii. 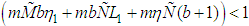 .Then for every
.Then for every 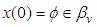 ,
, 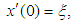 the Multi-fractional order impulsive nonlocal initial value control problem(3.1) without Neutral infinite delay has a unique mild solution
the Multi-fractional order impulsive nonlocal initial value control problem(3.1) without Neutral infinite delay has a unique mild solution 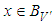 for every control
for every control 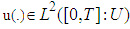 that is
that is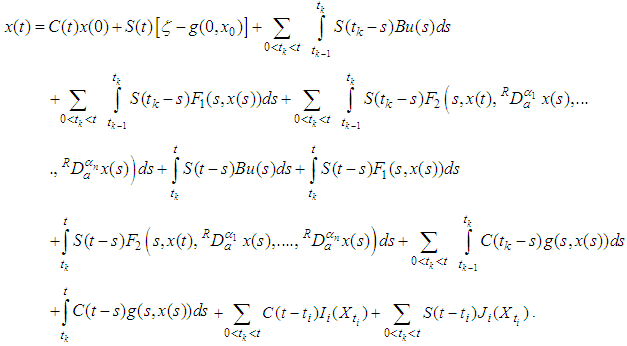 Proof: Let
Proof: Let 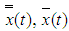 be two local mild solution of the nonlocal initial value impulsive control problem by equation (3.1) on the interval
be two local mild solution of the nonlocal initial value impulsive control problem by equation (3.1) on the interval  we must prove:
we must prove: 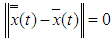 , Assume that
, Assume that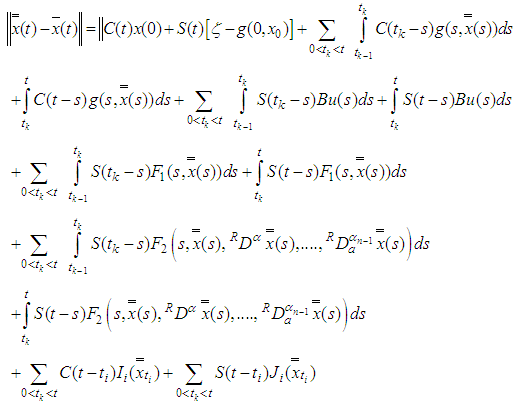
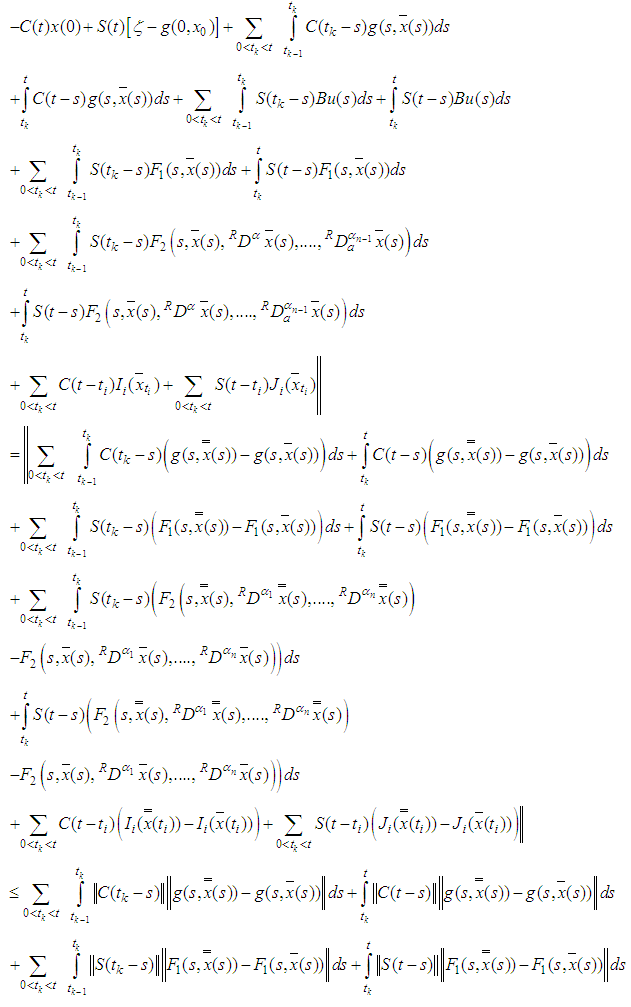
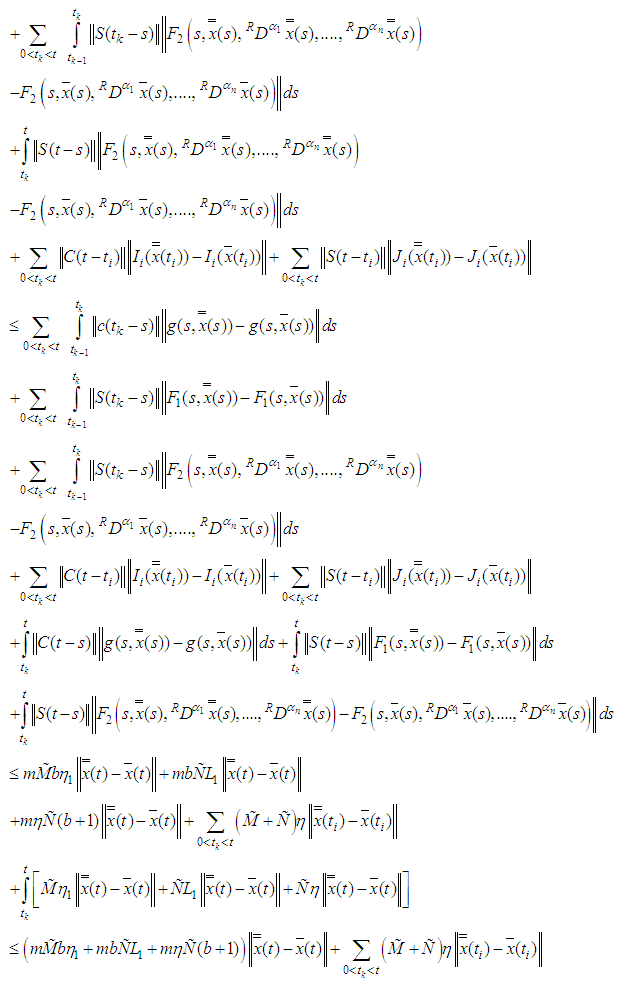
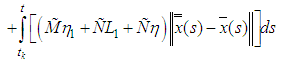 Set
Set 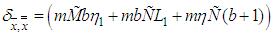 . Now,
. Now, 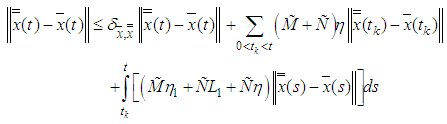
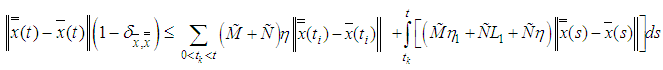
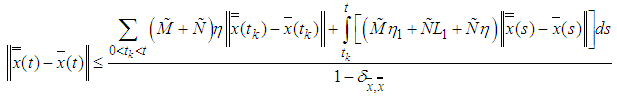 by (3.5), hence
by (3.5), hence 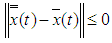 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML