1. Introduction

Now-a-days Bayesian approach is widely used for decision-making. In this paper, we have applied Bayesian approach in Markov chain based logistic model. Markov chain models can be used in analyzing longitudinal data. There is several discrete time Markov chain models proposed for analyzing repeated categorical data over decades. To analyze the binary sequence of presence or absence of diseases, Muenz and Rubinstein [10] introduced a discrete time Markov chain for expressing the transition probabilities in terms of covariates. The technique suggests by them is applicable for first order Markov model. For analyzing sequences of ordinal data from relapsing and remitting of a disease, Albert [1] developed a finite Markov chain model. In addition, Albert and Waclawiw [2] developed a class of quasilikelihood models for a two state Markov chain with stationary transition probabilities for heterogeneous transitional data. Raftery [14], Raftery and Tavare [13] proposed a higher order Markov chain model with dependence on contribution of the past transitions. Islam and Chowdhury [8] applied a three state Markov model for analyzing covariate dependence, also Islam and Chowdhury [7] presented a higher order version of the covariate dependent Markov model. For analyzing repeated observations, there is a renewed interest in the development of multivariate models based on Markov chains. These models can be employed for analyzing data generated from meteorology, epidemiology and survival analysis, reliability, econometric analysis, biological concerns, etc. Muenz and Rubinstein [10] employed logistic regression models to analyze the transition probabilities from one state to another. The estimation for first-order Markov models is quite straight forward, but still there is serious lack of generalization in estimation and testing for models applicability for higher order Markov chains. Islam and Chowdhury [7] provided a further generalization for covariate dependent higher order models. Following Azzalini [3], Heagerty and Zeger [5] presented a class of marginalized transition models (MTM) and Heagerty [4] proposed a class of generalized MTMs to allow serial dependence of first or higher order. These models are computationally tedious and the form of serial dependence is quite restricted. Heagerty [4] provided derivatives for score and information computations. Muenz and Rubinstein [10] introduced a discrete time Markov chain for expressing the transition probabilities in terms of function of covariates for a binary sequence of presence or absence of a disease. Islam, Chowdhury and Singh [6] suggest covariate dependence in a higher order Markov models is examined. The proposed model and inference procedures are simple and the covariate dependence of the transition probabilities of any order can be examined without making the underlying model complex. Another advantage of the model lies in the fact that the estimation and test procedures for both the specific parameter of interest and the overall model remain easy for practical applications for any longitudinal data. A simple alternative is also proposed. Applications are illustrated using maternal morbidity during pregnancy.

In this paper, an attempt is made to estimate the probability of being pregnancy complicacies of women according to the characteristics of the women and estimate the parameters by Bayesian approach and method of maximum likelihood approach. This characteristics or variables may often be related to each other. Higher difficulties occur to any miscarriage, economic status and age at marriage in this study.

2. Model

Muenz and Rubinstein [10] in 1985 proposed a two state Markov chain to model a discrete time-binary sequence. The transition matrix of the chain is:

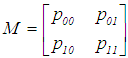where 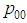denotes the transition probabilities from 0 to 0 and 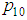is the transition probability from 1 to 0. At each time point, a vector of length two contains the probability of outcome of interest and its complement.

The first such vector (row) is P(1) = (p (1), 1 –p (1)), with the first element equal to the probability of the complement of the event of interest.

The matrix M and initial vector P(1) suffice to characterize the Markov chain. After time point 1, the vector of occupation probabilities is:

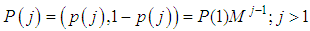Muenz and Rubinstein [10] proposed model the transition probabilities 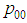and 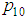by logistic regressions.

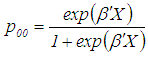and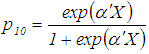

The vector X contains covariates and for the qth person in the study is equal to, 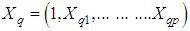. There are two logistic regressions, one having parameter vector 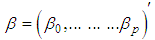and the other having parameter vector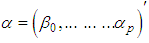. Large positive (negative) values of 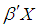and 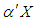yield large (small) transition probabilities. Since the transition matrix is a function of covariates, P (j) relates the occupation probabilities to the initial state for each pattern of covariates.

For transition 0 to 0

For binary random variable 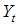with covariate 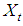the joint density function is as

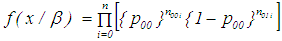where, 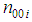and 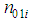are the number of transitions.

3. Bayesian Approach

In this study, we use the Bayesian paradigm to make inferences about parameters of the model [10] for pregnancy complication data.

3.1. Prior and Posterior Distribution

In Bayesian analysis prior and posterior distribution are important. Since the parameters of Markov model of 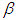lies between 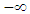to 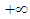, then according to Jeffrey’s non-informative prior [15] of 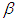are 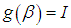. Where, I represent unit vector.

Then the posterior density of 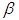for the given sample is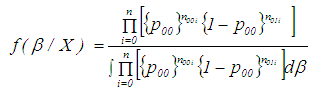

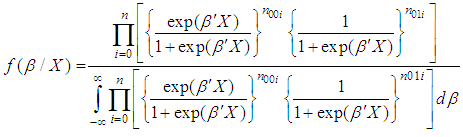
3.2. Bayes Estimators under Squared Error Loss Function

The squared error loss function is defined as

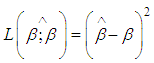For squared error loss function, Bayes estimators are the mean of the posterior density [11]

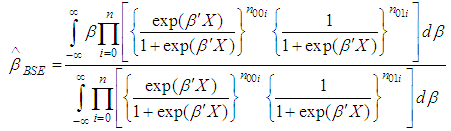The two integrals appear in the ratio cannot be solved to have a closed form. For evaluating them, we use the Lindley [12] approximation.

We have,

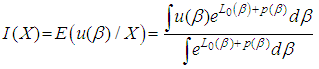where, 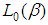is the log likelihood and 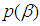is the logarithm prior distribution.

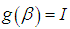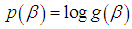Since, then or,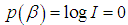

Then according to Lindley, I(X) can be approximately evaluated as

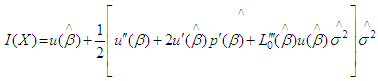where, 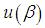is the functional form of the parameter 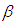, which is expected to posterior density and 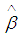is the maximum likelihood [10] estimator of .

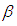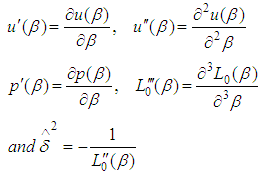Now we know that the likelihood function of binary dependence Markov model is

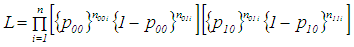Therefore,

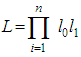Taking log on both sides

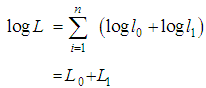where, 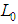and 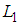are the likelihood function of transition 0 to 0 and 1 to 0 respectively.

Now considering

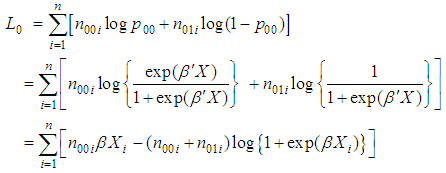Differentiating both sides with respect to 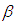, we have

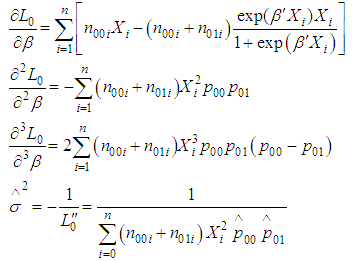Therefore, Bayes estimator under squared error loss function is

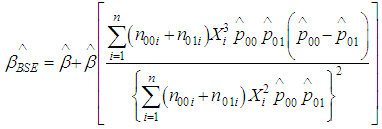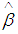where is the maximum likelihood [10] estimate of .

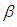If 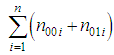is large then Bayes estimator tends to maximum likelihood estimator.

In addition, the same way we estimate the parameters of the transition 1 to 0.

4. Bayesian Credible Interval

If 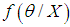is the posterior distribution given the sample, we may be interested in finding an interval such that

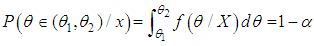This interval is called 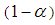100% Bayesian credible [9] interval of .

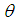In Bayesian analysis, credible interval becomes the counterpart of the classical confidence interval, also credible interval may be unique for all models. The Bayesian credible interval, on the other hand, has a direct probability interpretation 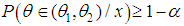and is completely determined from the current observed data x and the prior distribution.

5. Numerical Analysis

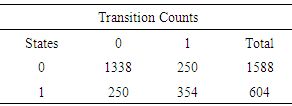
The covariate dependent Markov model proposed in this paper is applied to the pregnancy complication data conducted from BIRPERHT data for the period November 1992 to December 1993. The data were collected using both cross-sectional and prospective study designs. A multistage sampling design was used for collecting the data for this study. Districts were selected randomly in the first stage, one district from each Division. Then Thanas were selected randomly in the second stage, one Thana from each of the selected Districts. At the third stage, two Unions were selected randomly from each selected Thana. The subjects comprised of pregnant women with less than 6 months duration in the selected Unions. All the selected pregnant women from the selected Unions were followed on regular basis (roughly at an interval of 1 month) throughout the pregnancy. Again, the subjects were followed at the time of delivery for a full- term pregnancy and 90 days after delivery or 90 days after any other pregnancy outcome. A total of 1059 pregnant women were interviewed in the follow-up component of the study. The following pregnancy complications are considered under the complications in this study: hemorrhage, fits, convulsion, edema, excessive vomiting, and cough or fever for more than three days. If hemorrhage, fits, convulsion, edema, excessive vomiting, and cough or fever for more than three days occurred to the respondents, we considered complications and was coded as 1, if no complications then coded as 0. The explanatory variables are: age at marriage (15 years or lower, more than 15 years), economic status (lower or upper), any miscarriage (yes, no). The number of transitions for the two-state Markov chain of first order is displayed in Table 1.

Table 1. Transition counts of Markov chain for first orders of pregnancy complication of different flow-up

Estimate the Muenz-Rubinstein model using pregnancy complication data. In this study, we have used three covariates because of complexity to fit the model. Three highly significant covariates are used in our study. Bayesian approaches have been applied for estimating the parameter of the above model.

5.1. Comparison between Credible Interval and Confidence Interval

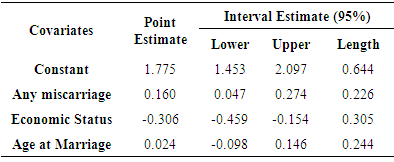
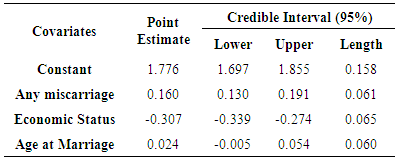
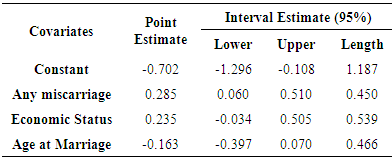
Confidence intervals for maximum likelihood estimators and credible intervals of Bayesian estimators under squared error loss function were calculated for Muenz-Rubinstein model and two types of transition are presented in the following table.

For 0 to 0 transition

Table 2. Confidence interval for maximum likelihood estimators

Table 3. Credible interval for Bayesian estimator under squared error loss function

From the above results, we have found that the length of Bayesian credible is lower than the length of confidence interval for all covariates.

Moreover, 1 to 0 transitions

Table 4. Confidence interval for maximum likelihood estimators

Table 5. Credible interval for Bayesian estimator under squared error loss function

Therefore, from the above tables it is also seen that, Baysian credible intervals are smaller length than confidence interval in 1 to 0 transitions. Therefore, we can say that Bayesian approach provides better result than usual method maximum approach in Muenz-Rubinstein model. In addition, economic status is negatively associated, any miscarriage and age at marriage are positively associate with pregnancy complication.

All the numerical analysis was performed by R-Language (Version-2.10.0).

6. Conclusions

Markov chain is very important part in real world situation. Its application increasing day by day, in this study we applied pregnancy complication data and only three covariates were used because complexity of the model. Meanwhile different types of approach were used for estimating the parameters in this model. In Bayesian approach under squared error of loss function were used and compare with method of maximum likelihood and we have found that length of Bayesian credible interval is smaller than length of confidence interval for all covariates in two types of transitions.

From the above analysis, we conclude that Bayes estimators under squared error loss function give better result in Muenz Rubinstein model. An application is included in this paper to illustrate the use of the proposed model for real life problems.