Gurjeet Singh Walia1, Harinder Kaur2, M. K. Sharma2
1Department of Math., Stat. & Physics, Punjab Agricultural University, Ludhiana, India
2Department of Statistics, Punjabi University, Patiala, India
Correspondence to: Gurjeet Singh Walia, Department of Math., Stat. & Physics, Punjab Agricultural University, Ludhiana, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In the present paper, we propose two ratio-type estimators of population mean of study variable 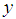 , using transformation based on known information of minimum
, using transformation based on known information of minimum 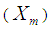 and maximum
and maximum 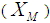 value of the auxiliary variable X. The expressions for bias and mean square error, up to the first degree of approximation, of proposed estimators are obtained. The comparisons of the proposed estimators are made with the existing ones with respect to bias and mean square error theoretically. The theoretical results are supported numerically and graphically. It has been shown that the proposed estimators are better than the existing ones under some conditions.
value of the auxiliary variable X. The expressions for bias and mean square error, up to the first degree of approximation, of proposed estimators are obtained. The comparisons of the proposed estimators are made with the existing ones with respect to bias and mean square error theoretically. The theoretical results are supported numerically and graphically. It has been shown that the proposed estimators are better than the existing ones under some conditions.
Keywords:
Auxiliary variable, Bias, Linear transformation, Mean square error, Ratio estimator, Simple random sampling without
Cite this paper: Gurjeet Singh Walia, Harinder Kaur, M. K. Sharma, Ratio Type Estimator of Population Mean through Efficient Linear Transformation, American Journal of Mathematics and Statistics, Vol. 5 No. 3, 2015, pp. 144-149. doi: 10.5923/j.ajms.20150503.06.
1. Introduction
To increase the efficiency of the proposed estimator of population mean of the study variable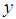 , we use the information of auxiliary variable
, we use the information of auxiliary variable 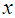 which is highly correlated with. Many authors viz. Sisodia and Dwivedi [1], Mohanty and Sahoo [2], Singh and Tailor [3], Khoshnevisan et al. [4], Gupta and Shabbir [5], Iqbal and Maqbool [6], Mehta and Sharma [7] etc. have adapted transformation method on auxiliary variable by using several known parameters such as
which is highly correlated with. Many authors viz. Sisodia and Dwivedi [1], Mohanty and Sahoo [2], Singh and Tailor [3], Khoshnevisan et al. [4], Gupta and Shabbir [5], Iqbal and Maqbool [6], Mehta and Sharma [7] etc. have adapted transformation method on auxiliary variable by using several known parameters such as 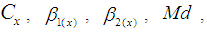
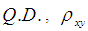 to reduce the bias and mean square error.In literature, the classical ratio estimator for population mean
to reduce the bias and mean square error.In literature, the classical ratio estimator for population mean 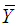 is defined as,
is defined as,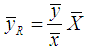 | (1.1) |
The bias and MSE of 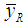 , up to first order of approximation, is
, up to first order of approximation, is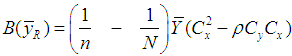 | (1.2) |
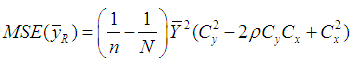 | (1.3) |
Sisodia and Dwivedi [1] using the information of  and
and 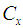 , defined ratio-type estimator for population mean
, defined ratio-type estimator for population mean 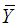 as
as 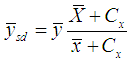 | (1.4) |
where 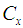 is the known population coefficient of variation of the auxiliary variable
is the known population coefficient of variation of the auxiliary variable  . The bias and MSE of
. The bias and MSE of 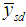 , up to first order of approximation, is
, up to first order of approximation, is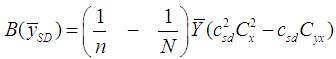 | (1.5) |
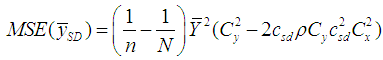 | (1.6) |
Where 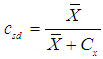 is a constant.Use of higher order parameters in the proposed estimators restricts their applicability. To overcome such type of restrictions, Mohanty and Sahoo [2] using known minimum
is a constant.Use of higher order parameters in the proposed estimators restricts their applicability. To overcome such type of restrictions, Mohanty and Sahoo [2] using known minimum  and maximum
and maximum 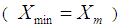 values besides population mean
values besides population mean 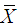 of auxiliary variable
of auxiliary variable 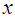 and then taking the transformation on auxiliary variable as,
and then taking the transformation on auxiliary variable as,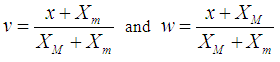 defined two estimators of
defined two estimators of 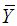 as
as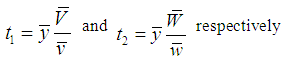 | (1.7) |
The expressions for bias and MSE of these estimators, up to first order of approximation, are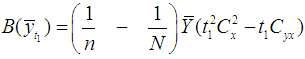 | (1.8) |
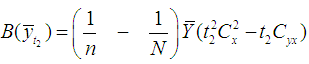 | (1.9) |
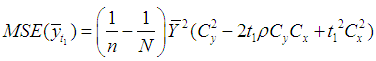 | (1.10) |
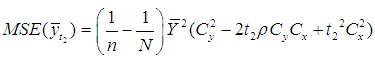 | (1.11) |
where 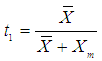 and
and 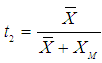 are constants respectively.It is to be noted that the transformations in
are constants respectively.It is to be noted that the transformations in 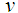 and
and 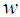 depend upon both
depend upon both 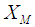 and
and 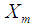 but estimators generated through these transformations depend only upon
but estimators generated through these transformations depend only upon 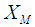 and
and 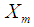 respectively. To utilize the information on both
respectively. To utilize the information on both 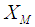 and
and 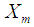 , in this paper, we propose a modified ratio-type estimator of population mean in simple random sampling using transformation on auxiliary variable in different forms. The expressions for bias and mean square error have been obtained. The comparison has been made with Classical ratio estimator, Mohanty and Sahoo [2] and Sisodia and Dwivedi [1]. The results have also been illustrated numerically and graphically.
, in this paper, we propose a modified ratio-type estimator of population mean in simple random sampling using transformation on auxiliary variable in different forms. The expressions for bias and mean square error have been obtained. The comparison has been made with Classical ratio estimator, Mohanty and Sahoo [2] and Sisodia and Dwivedi [1]. The results have also been illustrated numerically and graphically.
2. Sampling Design and Terminology
A simple random sample of size 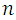 is drawn from a finite population of size
is drawn from a finite population of size 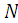 and both auxiliary variable
and both auxiliary variable 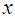 and study variable
and study variable 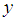 are measured on it.Let
are measured on it.Let 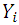 and
and 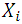 denote the respective values of variables
denote the respective values of variables 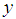 and
and 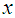 on the
on the 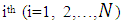 unit of the population. Corresponding small letters denote the values in the sample.Taking,
unit of the population. Corresponding small letters denote the values in the sample.Taking,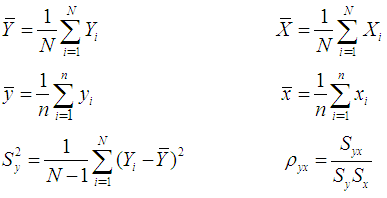
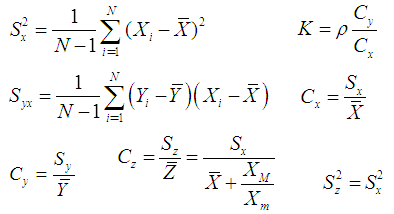 Defining,
Defining, So we have,
So we have,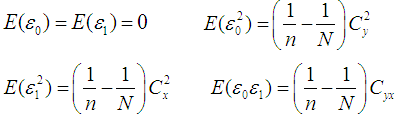
3. Proposed Estimator
Using known minimum 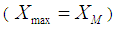 and maximum
and maximum 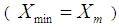 values besides population mean
values besides population mean 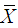 of auxiliary variable
of auxiliary variable 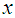 and then taking the transformation on auxiliary variable as
and then taking the transformation on auxiliary variable as 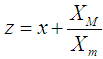 , we propose an estimator of
, we propose an estimator of 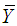 as
as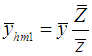 | (3.1) |
When 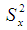 is also known, we propose an another estimator of population mean
is also known, we propose an another estimator of population mean 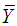 as,
as,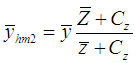 | (3.2) |
To find the bias and the MSE of the estimator 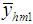 , we expand
, we expand 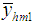 in terms of
in terms of 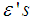 , up to the second degree of approximation, as
, up to the second degree of approximation, as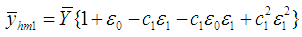 | (3.3) |
where 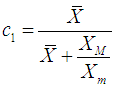 Taking the expectation in (3.3), we obtain
Taking the expectation in (3.3), we obtain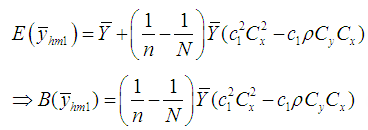 | (3.4) |
Using the expression (3.3), the mean square error of the proposed estimator 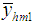 , up to the first order of approximation, is
, up to the first order of approximation, is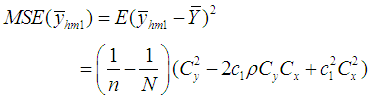 | (3.5) |
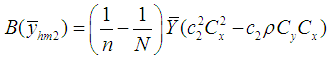 | (3.6) |
and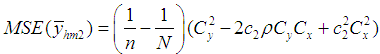 | (3.7) |
where 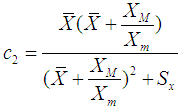 We have proved the following theorems:Theorem 3.1. Up to the first order of approximation, the bias of estimator
We have proved the following theorems:Theorem 3.1. Up to the first order of approximation, the bias of estimator 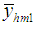 is
is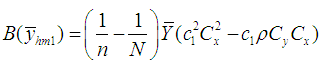 and its MSE is
and its MSE is 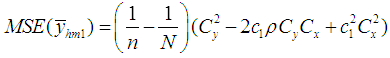 Theorem 3.2. Up to the first order of approximation, the bias of estimator
Theorem 3.2. Up to the first order of approximation, the bias of estimator 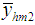 is
is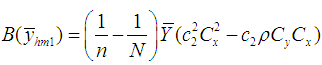 and its MSE is
and its MSE is 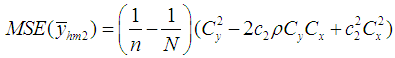
4. Comparison
First, we compare the bias of the proposed estimators 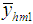 and
and 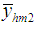 one by one with Classical ratio estimator
one by one with Classical ratio estimator 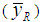 , Mohanty and Sahoo [2] estimators
, Mohanty and Sahoo [2] estimators 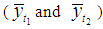 , and Sisodia and Dwivedi [1] estimator
, and Sisodia and Dwivedi [1] estimator 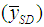 .Up to first order of approximation, we have
.Up to first order of approximation, we have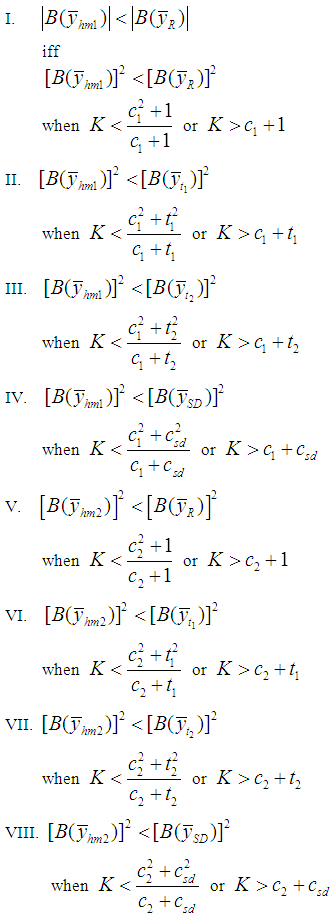 Second, we compare MSE of the proposed estimators
Second, we compare MSE of the proposed estimators 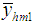 and
and  one by one with Classical ratio estimator
one by one with Classical ratio estimator 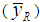 , Mohanty and Sahoo [2] estimators
, Mohanty and Sahoo [2] estimators 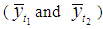 , and Sisodia and Dwivedi [1] estimator
, and Sisodia and Dwivedi [1] estimator  .
.

5. Numerical
To have the rough idea about the performance of the proposed estimators over the existing one, we consider a real finite population presented in Cochran [8] on page 34. This data set concerns food cost (as study variable) and weekly income (as auxiliary variable). Note that we omitted the data of 1 family because it was an outlier. The values of the population parameters are given in Table 1. The Bias, MSE and relative efficiency of proposed estimators with respect to Classical ratio estimator 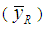 , Mohanty and Sahoo [2] estimators
, Mohanty and Sahoo [2] estimators 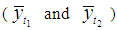 , and Sisodia and Dwivedi [1] estimator
, and Sisodia and Dwivedi [1] estimator 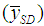 are given in Table 2 and Table 3 respectively. The results are also illustrated graphically.
are given in Table 2 and Table 3 respectively. The results are also illustrated graphically.Table 1. Parameters and Constants of the Population
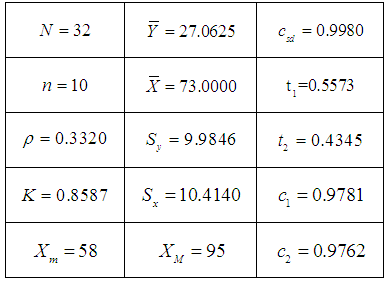 |
| |
|
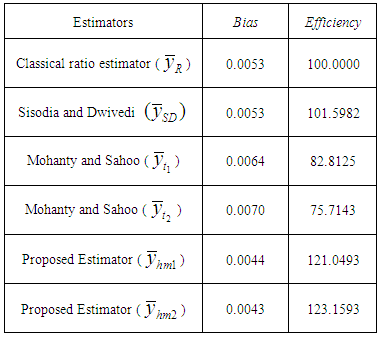
Table 2. Bias and Relative Efficiencies of Existing and Proposed Estimators
 |
| |
|
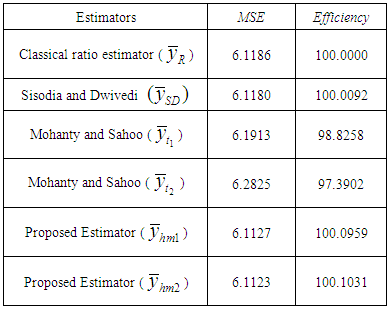
Table 3. MSE and Relative Efficiencies of Existing and Proposed Estimators
 |
| |
|
 | Figure 1. Bias and Relative Efficiencies of Existing and Proposed Estimators |
 | Figure 2. MSE and Relative Efficiencies of Existing and Proposed Estimators |
6. Conclusions
From the Table 2 and Table 3, we observe that although there is small increase in efficiency of the proposed estimators w. r. t. the MSE yet there is a significant increase in efficiency w. r. t. the bias. So we conclude that where we have to give the more weightage to precision as compared to the accuracy, then the proposed estimators with new linear transformation are recommended to use.
References
| [1] | Sisodia B.V.S. and Dwivedi V.K., “A modified ratio estimator using coefficient of variation of auxiliary variable”, Journal of the Indian Society of Agricultural Statistics, 33: 13-18, 1981. |
| [2] | Mohanty S. and Sahoo J., “A note on improving the ratio method of estimators through linear transformation using certain known population parameters”, Sankhya B, 57(1), 93-102, 1995. |
| [3] | Singh H.P. and Tailor R., “Use of known correlation coefficient in estimating the finite population mean”. Statistics in Transition, 6, 4, p-555-560, 2003. |
| [4] | Khoshnevisan M., Singh P., Chauhan P., Sawan N. and Smarandache F., “A general family of estimators for estimating population mean using known value of some population parameters”. Far East Journal of Theoretical Statistics, 22, p-181-191, 2007. |
| [5] | Gupta S. and Shabbir J., “On improvement in estimating the population mean in simple random sampling”. Journal of Applied Statistics, Vol.35, No.5, 559-566, 2008. |
| [6] | Iqbal Jeelani M. and Maqbool S., “Modified ratio estimators of population mean using linear combination of co-efficient of skewness and Q.D.” International Journal of Modern Mathematical. Sciences, 6(3); 174-183, 2013. |
| [7] | Mehta Netu and Latika Sharma, “A modification over ratio estimator using empirical data” Global Research Analysis (International).Statistics; Vol:2; Issue:1, ISSN No 2277-8160, 2013. |
| [8] | Cochran W.G., “Sampling Techniques”. (3rd ed.), Jhon Wiley and Sons, New York. 1977. |

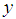 , using transformation based on known information of minimum
, using transformation based on known information of minimum 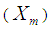 and maximum
and maximum 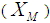 value of the auxiliary variable X. The expressions for bias and mean square error, up to the first degree of approximation, of proposed estimators are obtained. The comparisons of the proposed estimators are made with the existing ones with respect to bias and mean square error theoretically. The theoretical results are supported numerically and graphically. It has been shown that the proposed estimators are better than the existing ones under some conditions.
value of the auxiliary variable X. The expressions for bias and mean square error, up to the first degree of approximation, of proposed estimators are obtained. The comparisons of the proposed estimators are made with the existing ones with respect to bias and mean square error theoretically. The theoretical results are supported numerically and graphically. It has been shown that the proposed estimators are better than the existing ones under some conditions.
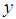 , we use the information of auxiliary variable
, we use the information of auxiliary variable 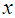 which is highly correlated with. Many authors viz. Sisodia and Dwivedi [1], Mohanty and Sahoo [2], Singh and Tailor [3], Khoshnevisan et al. [4], Gupta and Shabbir [5], Iqbal and Maqbool [6], Mehta and Sharma [7] etc. have adapted transformation method on auxiliary variable by using several known parameters such as
which is highly correlated with. Many authors viz. Sisodia and Dwivedi [1], Mohanty and Sahoo [2], Singh and Tailor [3], Khoshnevisan et al. [4], Gupta and Shabbir [5], Iqbal and Maqbool [6], Mehta and Sharma [7] etc. have adapted transformation method on auxiliary variable by using several known parameters such as 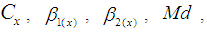
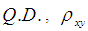 to reduce the bias and mean square error.In literature, the classical ratio estimator for population mean
to reduce the bias and mean square error.In literature, the classical ratio estimator for population mean 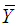 is defined as,
is defined as,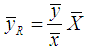
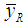 , up to first order of approximation, is
, up to first order of approximation, is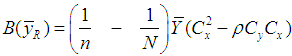
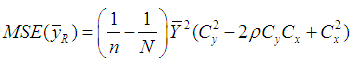
 and
and 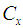 , defined ratio-type estimator for population mean
, defined ratio-type estimator for population mean 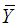 as
as 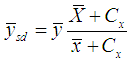
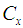 is the known population coefficient of variation of the auxiliary variable
is the known population coefficient of variation of the auxiliary variable  . The bias and MSE of
. The bias and MSE of 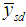 , up to first order of approximation, is
, up to first order of approximation, is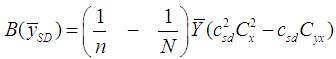
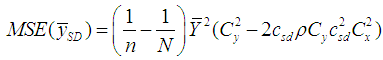
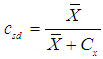 is a constant.Use of higher order parameters in the proposed estimators restricts their applicability. To overcome such type of restrictions, Mohanty and Sahoo [2] using known minimum
is a constant.Use of higher order parameters in the proposed estimators restricts their applicability. To overcome such type of restrictions, Mohanty and Sahoo [2] using known minimum  and maximum
and maximum 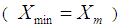 values besides population mean
values besides population mean 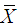 of auxiliary variable
of auxiliary variable 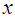 and then taking the transformation on auxiliary variable as,
and then taking the transformation on auxiliary variable as,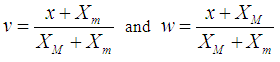 defined two estimators of
defined two estimators of 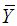 as
as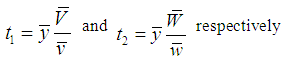
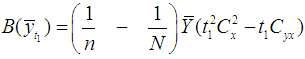
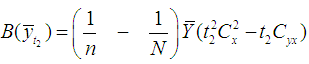
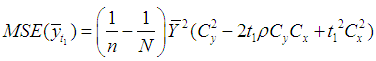
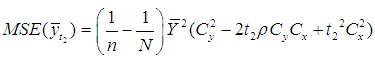
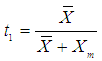 and
and 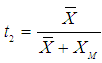 are constants respectively.It is to be noted that the transformations in
are constants respectively.It is to be noted that the transformations in 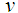 and
and 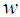 depend upon both
depend upon both 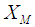 and
and 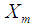 but estimators generated through these transformations depend only upon
but estimators generated through these transformations depend only upon 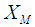 and
and 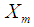 respectively. To utilize the information on both
respectively. To utilize the information on both 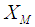 and
and 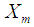 , in this paper, we propose a modified ratio-type estimator of population mean in simple random sampling using transformation on auxiliary variable in different forms. The expressions for bias and mean square error have been obtained. The comparison has been made with Classical ratio estimator, Mohanty and Sahoo [2] and Sisodia and Dwivedi [1]. The results have also been illustrated numerically and graphically.
, in this paper, we propose a modified ratio-type estimator of population mean in simple random sampling using transformation on auxiliary variable in different forms. The expressions for bias and mean square error have been obtained. The comparison has been made with Classical ratio estimator, Mohanty and Sahoo [2] and Sisodia and Dwivedi [1]. The results have also been illustrated numerically and graphically.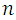 is drawn from a finite population of size
is drawn from a finite population of size 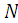 and both auxiliary variable
and both auxiliary variable 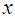 and study variable
and study variable 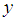 are measured on it.Let
are measured on it.Let 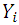 and
and 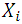 denote the respective values of variables
denote the respective values of variables 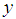 and
and 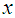 on the
on the 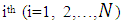 unit of the population. Corresponding small letters denote the values in the sample.Taking,
unit of the population. Corresponding small letters denote the values in the sample.Taking,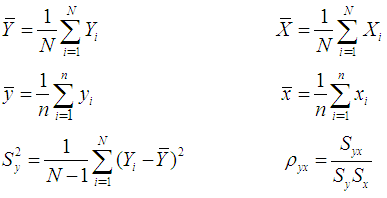
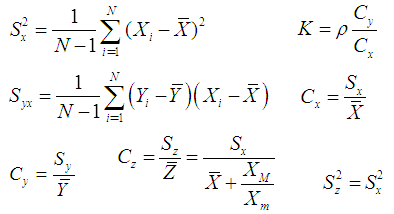 Defining,
Defining, So we have,
So we have,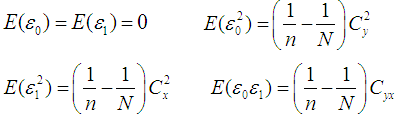
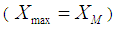 and maximum
and maximum 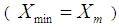 values besides population mean
values besides population mean 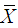 of auxiliary variable
of auxiliary variable 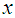 and then taking the transformation on auxiliary variable as
and then taking the transformation on auxiliary variable as 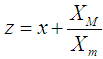 , we propose an estimator of
, we propose an estimator of 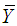 as
as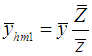
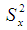 is also known, we propose an another estimator of population mean
is also known, we propose an another estimator of population mean 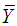 as,
as,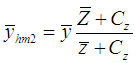
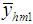 , we expand
, we expand 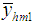 in terms of
in terms of 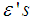 , up to the second degree of approximation, as
, up to the second degree of approximation, as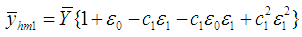
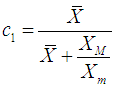 Taking the expectation in (3.3), we obtain
Taking the expectation in (3.3), we obtain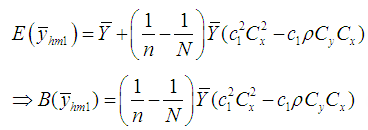
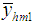 , up to the first order of approximation, is
, up to the first order of approximation, is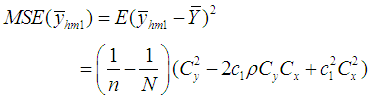
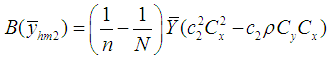
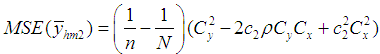
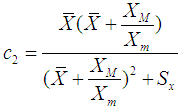 We have proved the following theorems:Theorem 3.1. Up to the first order of approximation, the bias of estimator
We have proved the following theorems:Theorem 3.1. Up to the first order of approximation, the bias of estimator 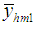 is
is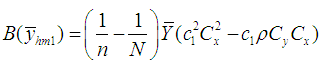 and its MSE is
and its MSE is 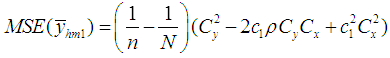 Theorem 3.2. Up to the first order of approximation, the bias of estimator
Theorem 3.2. Up to the first order of approximation, the bias of estimator 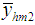 is
is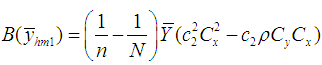 and its MSE is
and its MSE is 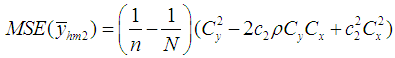
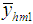 and
and 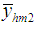 one by one with Classical ratio estimator
one by one with Classical ratio estimator 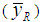 , Mohanty and Sahoo [2] estimators
, Mohanty and Sahoo [2] estimators 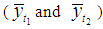 , and Sisodia and Dwivedi [1] estimator
, and Sisodia and Dwivedi [1] estimator 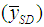 .Up to first order of approximation, we have
.Up to first order of approximation, we have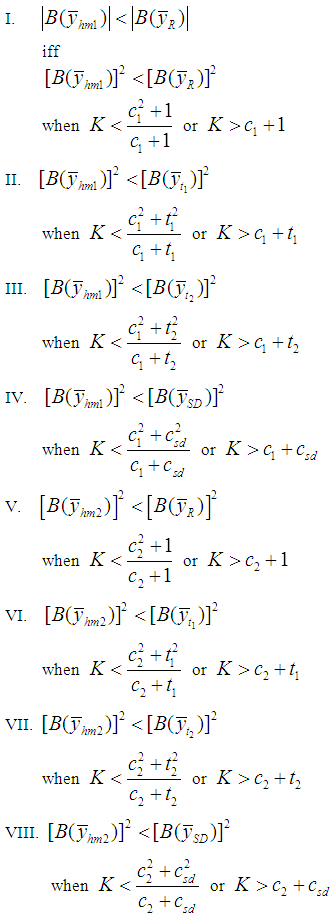 Second, we compare MSE of the proposed estimators
Second, we compare MSE of the proposed estimators 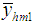 and
and  one by one with Classical ratio estimator
one by one with Classical ratio estimator 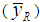 , Mohanty and Sahoo [2] estimators
, Mohanty and Sahoo [2] estimators  , and Sisodia and Dwivedi [1] estimator
, and Sisodia and Dwivedi [1] estimator  .
.

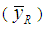 , Mohanty and Sahoo [2] estimators
, Mohanty and Sahoo [2] estimators 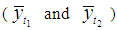 , and Sisodia and Dwivedi [1] estimator
, and Sisodia and Dwivedi [1] estimator 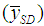 are given in Table 2 and Table 3 respectively. The results are also illustrated graphically.
are given in Table 2 and Table 3 respectively. The results are also illustrated graphically.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

