Chukwu A. U., Ogunde A. A.
Department of Statistics, University Of Ibadan, Department of Mathematics and Statistics, Federal Polytechnic Ado-Ekiti, Nigeria
Correspondence to: Ogunde A. A., Department of Statistics, University Of Ibadan, Department of Mathematics and Statistics, Federal Polytechnic Ado-Ekiti, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, a new five-parameter generalized version of the Gompertz-Mekaham distribution called Beta Gompertz-Mekaham (BGM) distribution is being introduced. It includes some well-known lifetime distributions as special sub-models. The new distribution is quite flexible and can have a decreasing, increasing, and bathtub-shaped failure rate function depending on its parameters making it effective in modeling survival data and reliability problems. Some comprehensive properties of the new distribution, such as closed-form expressions for the density, cumulative distribution, hazard rate function, the rth order moment, moment are provided. The maximum likelihood estimation of the BGM parameters as well as observed Fisher’s information matrix obtained. At the end, in order to show the capability of BMG over its sub models, an application to a real dataset illustrates its potentiality.
Keywords:
Beta generator, Gompertz-Mekaham distribution, Maximum likelihood estimation
Cite this paper: Chukwu A. U., Ogunde A. A., On the Beta Mekaham Distribution and Its Applications, American Journal of Mathematics and Statistics, Vol. 5 No. 3, 2015, pp. 137-143. doi: 10.5923/j.ajms.20150503.05.
1. Introduction
Modelling of interrelationship among naturally occurring phenomena is made possible by the use of distribution function and their properties. Thus a number of statistical distributions function and their generalization have been proposed and defined in the literature, most of which are found to be useful in studying naturally occurring phenomena particularly where the variables assure values between 0 and 1. Many useful properties of such distribution are revealed by transformation of random variables while another approach is the convolution technique which is rarely used. Among the useful distributions applicable to real life data and the logit of beta distribution are the beta-pareto (Akinsete and Lowe, 2008); beta-Laplace (Kozubowski and Nadarajah (2008); beta-Weibull (Famoye, et al 2005); beta-Normal (Eugene et al, 2002); beta-exponential (Nadarajah and Kotz, 2006); and beta-Gumbel (Nadarajah and Kot, 2004).
2. Gompertz Mekaham Distribution
The Gompertz-Makeham law states that the death rate is the sum of an age independent component (the Makeham term) and an age-dependent component (the Gompertz function) which increases exponentially with age. In a protected environment where external causes of death are rare (laboratory conditions, low mortality countries, etc.), the age-independent mortality component is often negligible. In a protected environment where external causes of death are rare (laboratory conditions, low mortality countries, etc.), the age-independent mortality component is often negligible. In this case the formula simplifies to a Gompertz law of mortality. In 1825, Benjamin Gompertz proposed an exponential increase in death rates with age.The Gompertz–Makeham law of mortality describes the age dynamics of human mortality rather accurately in the age window from about 30 to 80 years of age. At more advanced ages, some studies have found that death rates increase more slowly – a phenomenon known as the late-life mortality deceleration – but other studies disagree.A random variable X is distributed Gompert-Makeham if and only its pdf satisfies the below 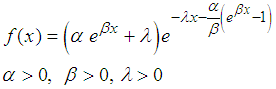 | (1) |
Its cumulative density function is 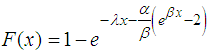 | (2) |
3. The Proposed Beta Gompertz Mekaham Distribution
The beta distribution has been widely used, applied, powerful and well known as a probability distribution to administer several kinds of problems in reliability analysis. In recent years, development focus on new techniques for building meaningful distributions, including the use of the logit of beta (the link function of the beta generalized distribution pioneered by Jones (2004)). The logit of beta introduced by Jones has probability density function (pdf).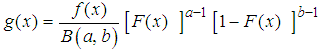 | (3) |
where 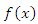 is the pdf of X.If we put (1) and (2) in (3) we have
is the pdf of X.If we put (1) and (2) in (3) we have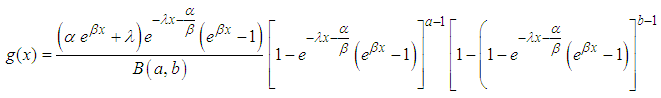 this simplifies to
this simplifies to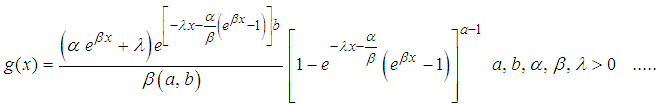 | (4) |
3.1. Statistical Properties
In this section the statistical properties of the proposed distribution will be investigated. This include asymptotic behaviour, verification of true probability function, cumulative density and hazard rate function.Asymptotic BehaviourWe seek to investigate the behaviour of the model in Equation (4) as 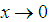 If
If 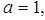 we have
we have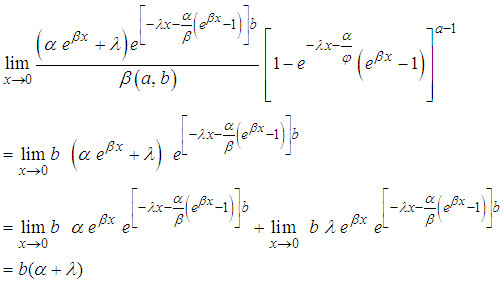 Investigation of Proper pdfHere, we seek to verify here whether the proposed distribution integrate to unity
Investigation of Proper pdfHere, we seek to verify here whether the proposed distribution integrate to unity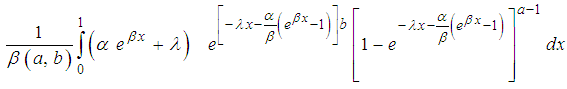 Let
Let 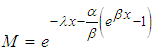
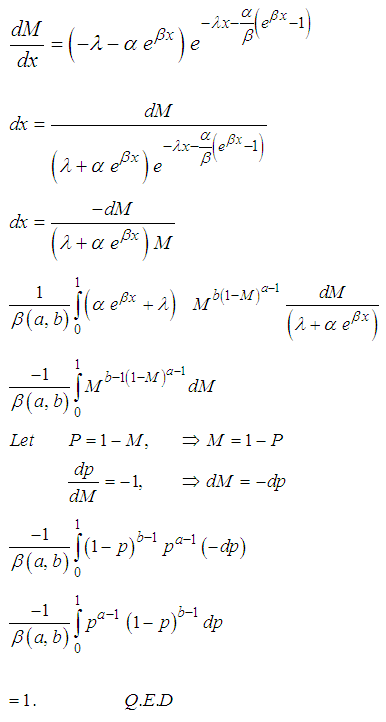
3.2. Cumulative Density Function
The distribution function of the beta Gompert Mekaham distribution is derived as follows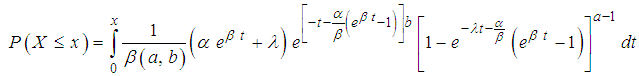 This reduces to
This reduces to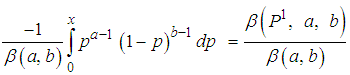
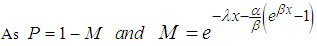 Finally,
Finally, 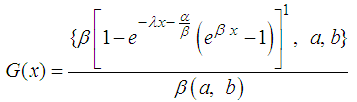 | (5) |
3.3. Hazard Rate Function
The hazard rate function is obtained using | (6) |
The above is Beta-Gompertz Mekaham Mortality Model When 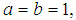 we have
we have 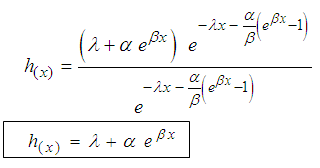 | (7) |
which is the hazard of Gompertz-Mekaham distribution, a Gompertz-Mekaham Mortality.
4. Estimation and Statistical Inference
Let 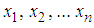 be a random variable distributed according (4) the likelihood function of vector of parameters given as
be a random variable distributed according (4) the likelihood function of vector of parameters given as 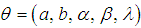 is
is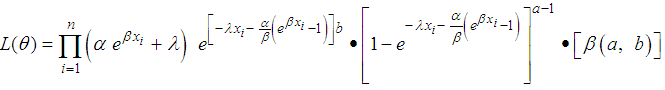 Then its log-likelihood function is
Then its log-likelihood function is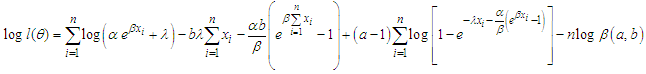 | (8) |
This is simplified as by noting that 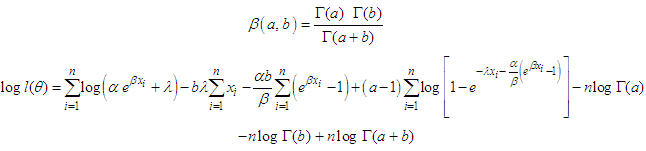 | (9) |
This is then differentiated with respect to 
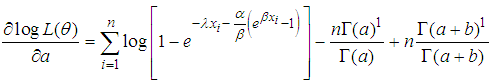 | (10) |
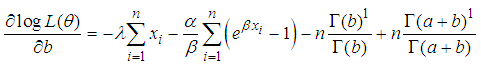 | (11) |
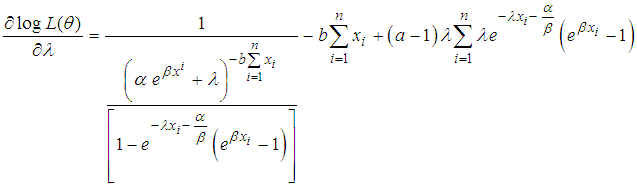 | (12) |
If we let 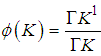 we have
we have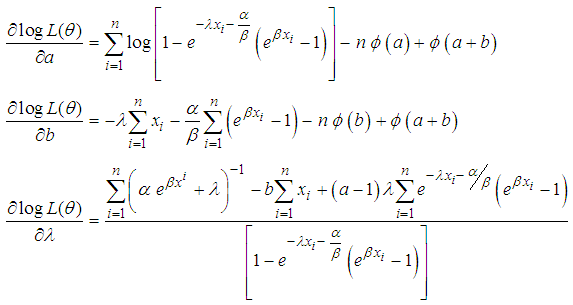
5. Application
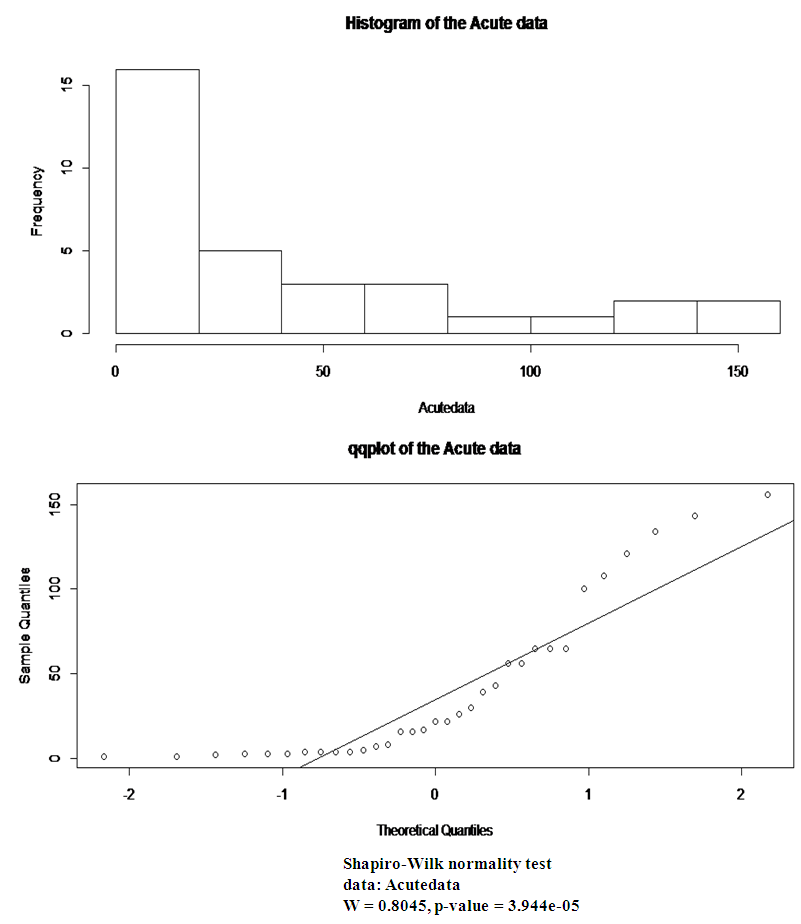
In this section, we fit the Beta Gompertz Mekaham distribution and its sub models to a survival data set that was analyzed by Feigl and Zelen(1965). The data represent the survival times, in weeks, of 33 patients suffering from acutemyelogeneous Leukaemia. The data can also be found at library SMIR of the R program(http://cran.r-project.org), are the following: 65, 156, 100, 134, 16, 108, 121, 4, 39, 143,56, 26, 22, 1, 1, 5, 65, 56, 65, 17, 7, 16, 22, 3, 4, 2, 3, 8, 4, 3, 30, 4, 43.The distribution of the data is skewed to the right. Below is the summary of resultsTable 1. Descriptive Statistics on Failure Time on Conditional System
 |
| |
|
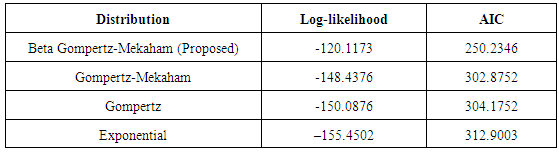
Table 2. Log likelihood and Alkaike Information Criterion of Models
 |
| |
|
 | Figure |
6. Conclusions
The Beta Gompertz-Mekaham distribution was defined and studied in this work. Various properties of the distribution were discussed. These include the asymptotic behaviors, Cumulative density function, hazard functions among others. Also we discussed the estimation of parameters by the method of maximum likelihood.Real life application indicates that new distribution apart from being more flexible has better representation of data than its sub models.
References
| [1] | Akinsete, A., Famoye, F. and Lee, C. (2008). The beta-Pareto distribution. Statistics 42, 547-563. |
| [2] | Chaudhry, M. A. and Zubair, S. M. (2002). On a Class of Incomplete Gamma Functions with Applications. Chapman and Hall, Boca Raton, Florida. |
| [3] | Cooray, K. and Amanda, M. M. A. (2008). A generalization of the half-normal distribution with applications to lifetime data. Communications in Statistics - Theory and Methods 37, 1323-1337. |
| [4] | Cordeiro, G. M. and Nadarajah, S. (2011). Closed-form expressions for moments of a class of beta generalized distributions. Brazilian Journal of Probability and Statistics 25, 14-33. |
| [5] | Eugene, N., Lee, C. and Famoye, F. (2002). Beta-normal distribution and its applications.Communications in Statistics - Theory and Methods 31, 497-512. |
| [6] | Exton, H. (1978). Handbook of Hypergeometric Integrals: Theory, Applications, Tables, Computer Programs. Halsted Press, New York. |
| [7] | Gupta, R. C., Gupta, P. L. and Gupta, R. D. (1998). Modeling failure time data by Lehmann alternatives. Communications in Statistics - Theory and Methods 27, 887-904. |
| [8] | Gupta, R. D. and Kundu, D. (1999). Generalized exponential distributions. Australian and New Zealand Journal of Statistics 41, 173-188. |
| [9] | Gupta, R. D. and Kundu, D. (2001). Exponentiated exponential family: an alternative to gamma and Weibull. Biometrical Journal 43, 117-130. |

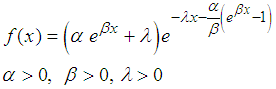
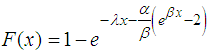
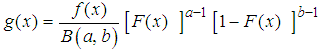
 is the pdf of X.If we put (1) and (2) in (3) we have
is the pdf of X.If we put (1) and (2) in (3) we have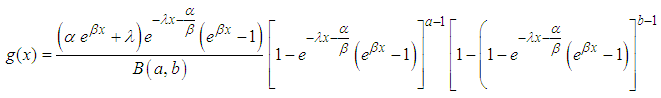 this simplifies to
this simplifies to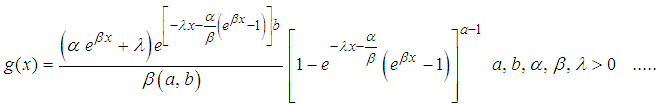
 If
If  we have
we have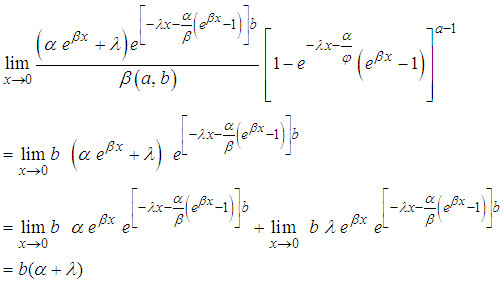 Investigation of Proper pdfHere, we seek to verify here whether the proposed distribution integrate to unity
Investigation of Proper pdfHere, we seek to verify here whether the proposed distribution integrate to unity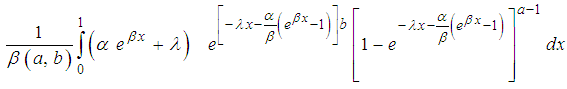 Let
Let 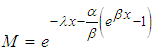
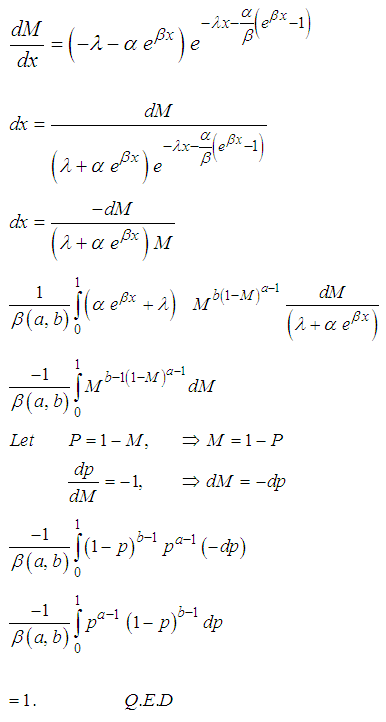
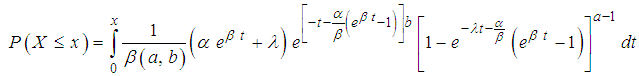 This reduces to
This reduces to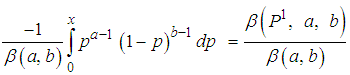
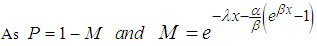 Finally,
Finally, 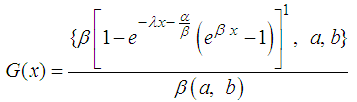

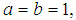 we have
we have 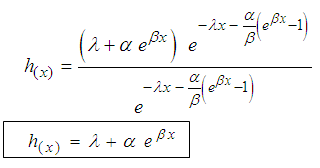
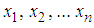 be a random variable distributed according (4) the likelihood function of vector of parameters given as
be a random variable distributed according (4) the likelihood function of vector of parameters given as 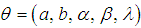 is
is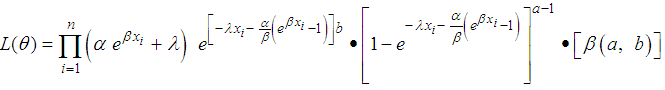 Then its log-likelihood function is
Then its log-likelihood function is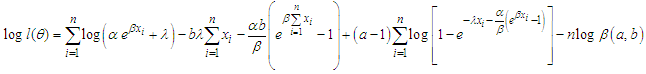
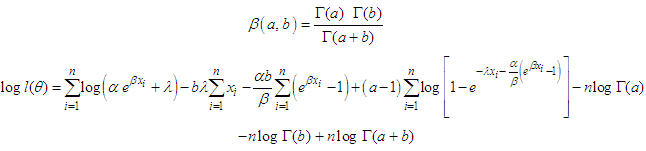
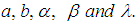
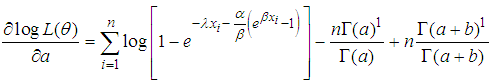
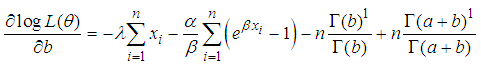
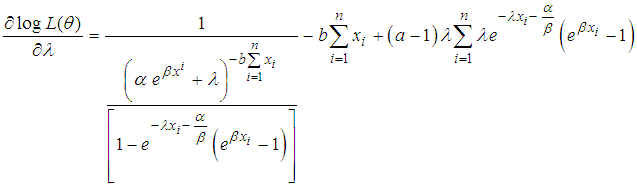
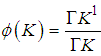 we have
we have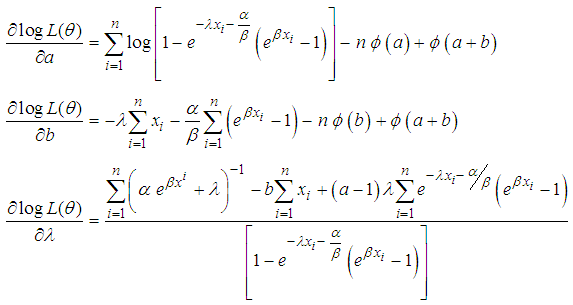
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

