Salah H. Abid, Sameer Q. Hasan, Uday J. Quaez
Mathematics department, Education College, Al-Mustansiriya University, Baghdad, Iraq
Correspondence to: Salah H. Abid, Mathematics department, Education College, Al-Mustansiriya University, Baghdad, Iraq.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we will study the Approximate controllability of fractional stochastic integro-differential equations which is derived by mixed type of fractional Brownian motion with Hurst parameter 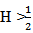 and wiener process in real separable Hilbert space. An example was stated as a application of our result.
and wiener process in real separable Hilbert space. An example was stated as a application of our result.
Keywords:
Approximate controllability, Mixed type of fractional Brownian motion, Fixed point contraction principle, Stochasticintegro- Differential equations, Mild solution, Control function
Cite this paper: Salah H. Abid, Sameer Q. Hasan, Uday J. Quaez, Approximate Controllability of Fractional Stochastic Integro-Differential Equations Driven by Mixed Fractional Brownian Motion, American Journal of Mathematics and Statistics, Vol. 5 No. 2, 2015, pp. 72-81. doi: 10.5923/j.ajms.20150502.04.
1. Introduction
The purpose of this paper is to prove the existence and approximate controllability of mild solution for the class of fractional stochastic integro-differential equations driven by mixed type of fractional Brownian motion with Hurst 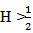 and wiener process. The following form is the system under our consideration,
and wiener process. The following form is the system under our consideration,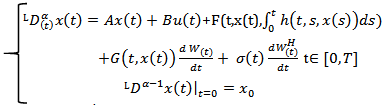 | (1) |
where 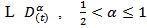 the Riemann-Liouville fractional derivative of order α. A: Dom(A) ⊂ X →X is the infinitesimal generator of strongly continuous compact semi group of bounded linear operators
the Riemann-Liouville fractional derivative of order α. A: Dom(A) ⊂ X →X is the infinitesimal generator of strongly continuous compact semi group of bounded linear operators 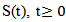 in X. x(.) takes the value in the real separable Hilbert space X such that for each
in X. x(.) takes the value in the real separable Hilbert space X such that for each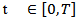 ,
, 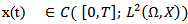
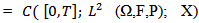 the banach space of all continuous functions from [0,T] in to
the banach space of all continuous functions from [0,T] in to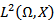 satisfying the condition
satisfying the condition 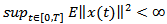 and
and 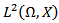 is a banach space of all F-measurable square integrable random variables with values in Hilbert space X equipped with the sup norm
is a banach space of all F-measurable square integrable random variables with values in Hilbert space X equipped with the sup norm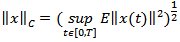
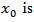 F0 –measurable X- valued random variable independent of W and
F0 –measurable X- valued random variable independent of W and 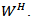
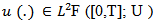 is the space of the Ft – adapted , U-valued measurable process u(t) on [0,T] such that
is the space of the Ft – adapted , U-valued measurable process u(t) on [0,T] such that 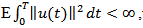 with norm
with norm 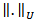 where U is a real separable Hilbert space. B is the linear bounded operator from U into X such that there exists constant
where U is a real separable Hilbert space. B is the linear bounded operator from U into X such that there exists constant 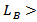
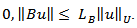
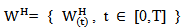 is a Q-fractional Brownian motion with Hurst index
is a Q-fractional Brownian motion with Hurst index 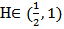 defined in a complete probability space
defined in a complete probability space 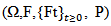 with values in a Hilbert space Y.
with values in a Hilbert space Y.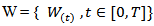 is a Q-l wiener process defined on
is a Q-l wiener process defined on 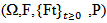 with values in a Hilbert space K.
with values in a Hilbert space K.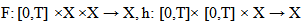 and
and 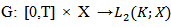 are continuous functions and uniformly bounded.
are continuous functions and uniformly bounded. 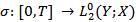 is a deterministic function the processes W and
is a deterministic function the processes W and 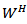 are independent.In the past few decades, the theory of fractional partial differential equations in both types deterministic and stochastic, have received a great deal of attention and play an important role in many applied scientific fields.The deterministic models often affected due to fractal noise, which is random or at least appears to be so. Therefore, the study of stochastic systems are more applicable in dynamical system theory. Random phenomena exist everywhere in the real world. Systems are often.Subjected to random perturbations. The existence of solution for some classes of Stochastic equations driven by fractional Brownian motion have been investigated by many authors, see, for example [4], [9], [19].The controllability of stochastic differential equations in infinite dimensional spaces have been investigated by many authors [6], [7], [8], [11], [12]. In recent years, sakthivel [15] derived a set of sufficient conditions for approximate controllability of nonlinear impulsive stochastic differential equations in a real separable Hilbert space by using the stochastic analysis theory and a fixed point. Zang and Li [20] studied the approximate controllability of fractional impulsive neutral stochastic differential equations with non-local conditions and infinite delay in Hilbert space. Guendouzi [18] studies the approximate controllability result of a class of dynamic control systems described by nonlinear fractional stochastic functional differential equations in Hilbert.Space driven by a fractional Brownian motion with Hurst parameter H > 1/2 by using the theory of fractional calculus and a fixed point theorm. Hamdy [5] studied the approximate controllability for impulsive neutral stochastic functional differential equations with finite delay and fractional Brownian motion in a Hilbert space by using semigroup theory, stochastic analysis, and Banach’s fixed point theorem.In this paper we will study the approximate controllability of nonlinear stochastic system. More precisely, we shall formulate and prove sufficient conditions for the Approximate controllability of fractional stochastic integro-differential equations driven by mixed type of fractional Brownian motion with Hurst
are independent.In the past few decades, the theory of fractional partial differential equations in both types deterministic and stochastic, have received a great deal of attention and play an important role in many applied scientific fields.The deterministic models often affected due to fractal noise, which is random or at least appears to be so. Therefore, the study of stochastic systems are more applicable in dynamical system theory. Random phenomena exist everywhere in the real world. Systems are often.Subjected to random perturbations. The existence of solution for some classes of Stochastic equations driven by fractional Brownian motion have been investigated by many authors, see, for example [4], [9], [19].The controllability of stochastic differential equations in infinite dimensional spaces have been investigated by many authors [6], [7], [8], [11], [12]. In recent years, sakthivel [15] derived a set of sufficient conditions for approximate controllability of nonlinear impulsive stochastic differential equations in a real separable Hilbert space by using the stochastic analysis theory and a fixed point. Zang and Li [20] studied the approximate controllability of fractional impulsive neutral stochastic differential equations with non-local conditions and infinite delay in Hilbert space. Guendouzi [18] studies the approximate controllability result of a class of dynamic control systems described by nonlinear fractional stochastic functional differential equations in Hilbert.Space driven by a fractional Brownian motion with Hurst parameter H > 1/2 by using the theory of fractional calculus and a fixed point theorm. Hamdy [5] studied the approximate controllability for impulsive neutral stochastic functional differential equations with finite delay and fractional Brownian motion in a Hilbert space by using semigroup theory, stochastic analysis, and Banach’s fixed point theorem.In this paper we will study the approximate controllability of nonlinear stochastic system. More precisely, we shall formulate and prove sufficient conditions for the Approximate controllability of fractional stochastic integro-differential equations driven by mixed type of fractional Brownian motion with Hurst 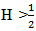 and wiener process in Hilbert space. The rest of this paper is organized as follows, in section 2, we will introduced some concepts, definitions and some lemmas of fractional stochastic calculus which are useful for us here. In section 3, we will prove our main result. Finally in section 4, as an application, an example will be stated in details.
and wiener process in Hilbert space. The rest of this paper is organized as follows, in section 2, we will introduced some concepts, definitions and some lemmas of fractional stochastic calculus which are useful for us here. In section 3, we will prove our main result. Finally in section 4, as an application, an example will be stated in details.
2. Preliminaries
In this section, we introduce some notations and preliminary results, needed to establish our results. Throughout this paper, let X, Y, K be real separable Hilbert spaces and 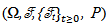 be a complete probability space with natural filtration
be a complete probability space with natural filtration 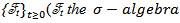 generated by therandom variables
generated by therandom variables 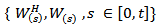 and the P-null set). We denote by L (K; X) the space of all bounded linear operators from K to X and L(Y; X) denote the space of all bounded linear operators from Y to X. For convenience we will use the same notation
and the P-null set). We denote by L (K; X) the space of all bounded linear operators from K to X and L(Y; X) denote the space of all bounded linear operators from Y to X. For convenience we will use the same notation  to denote the norms in K, Y, X,L (K;X), L(Y;X) and use
to denote the norms in K, Y, X,L (K;X), L(Y;X) and use 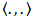 to the inner product of K , Y , X.Definition (2.1) [1]:A standard fractional Brownian motion with Hurst index H ∈ (0,1) is a Gaussian process
to the inner product of K , Y , X.Definition (2.1) [1]:A standard fractional Brownian motion with Hurst index H ∈ (0,1) is a Gaussian process 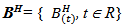 on (Ω, F, P) having the properties i.
on (Ω, F, P) having the properties i. 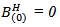 ii.
ii. 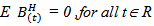 iii.
iii. 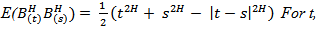
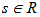 If
If 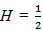 Then the increments of BH are non-correlated, and consequently independent. So BH is a standard Wiener Process which we denote further by B.-If H
Then the increments of BH are non-correlated, and consequently independent. So BH is a standard Wiener Process which we denote further by B.-If H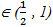 then the increments are positively correlated-If H
then the increments are positively correlated-If H 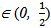 then the increments are negative correlatedMoreover, BH has the integral representation
then the increments are negative correlatedMoreover, BH has the integral representation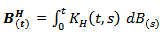 Where B is a standard Wiener process and the kernel
Where B is a standard Wiener process and the kernel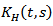 defined as
defined as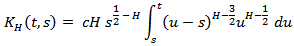 and
and 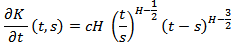
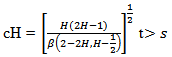 in the case
in the case 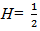 we shall use Ito Isometry
we shall use Ito Isometry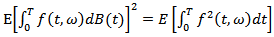 | (2) |
for every 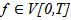 the class of functions such that
the class of functions such that 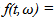
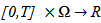 and f is measurable,
and f is measurable, 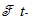 adapted and
adapted and 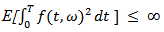 Suppose
Suppose 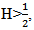 We denote by the set of step functions on [0, T]The integral of Φ∈ᶓ with respect to a standard fractional Brownian motion will be defined by,
We denote by the set of step functions on [0, T]The integral of Φ∈ᶓ with respect to a standard fractional Brownian motion will be defined by,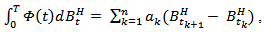 Where
Where 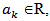
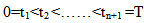 NOW, Let
NOW, Let 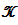 be the Hilbert space defined as the closure of ᶓ with respect to the scalar product
be the Hilbert space defined as the closure of ᶓ with respect to the scalar product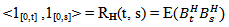 The mapping
The mapping 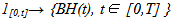 can be extended to an isometry between H and
can be extended to an isometry between H and 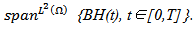 Let │H│ be the Banach space of measurable functions ' on [0, T], such that
Let │H│ be the Banach space of measurable functions ' on [0, T], such that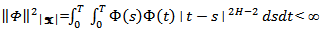 Lemma (2-1) [9]
Lemma (2-1) [9]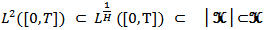 and for any
and for any 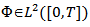 we have
we have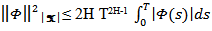 Now Suppose that there exists a complete orthonormal system
Now Suppose that there exists a complete orthonormal system 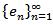 in Y. Let
in Y. Let 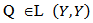 be the operator defined by
be the operator defined by 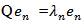 where
where 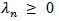 (n=1,2,….) are non-negative real numbers .With finite trace.Tr
(n=1,2,….) are non-negative real numbers .With finite trace.Tr 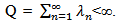 Analogically to Wiener processes in a Hilbert space, we defined A fractional Brwnian Motion on Y by using covariance operator Q as
Analogically to Wiener processes in a Hilbert space, we defined A fractional Brwnian Motion on Y by using covariance operator Q as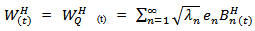 Where
Where 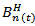 are standard fractional Brownian motions mutually independent on
are standard fractional Brownian motions mutually independent on 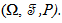 In order to defined stochastic integral with respect to the Q-fractional Brownian motion.We introduce the space
In order to defined stochastic integral with respect to the Q-fractional Brownian motion.We introduce the space 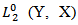 of all Q-Hilbert- Schmidt operators that is with the inner product
of all Q-Hilbert- Schmidt operators that is with the inner product 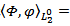
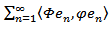 is a separable Hilbert space. L2(K;X) the space of all Hilbert-Schmidt operators acting between K and X equipped with the Hilbert-Schmidt norm
is a separable Hilbert space. L2(K;X) the space of all Hilbert-Schmidt operators acting between K and X equipped with the Hilbert-Schmidt norm 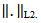 Lemma (2-2)Let
Lemma (2-2)Let 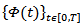 be a deterministic function with values in
be a deterministic function with values in 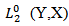 The stochastic integral of Φ with respect to
The stochastic integral of Φ with respect to 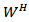 is defined by
is defined by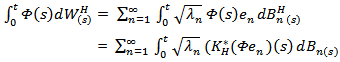 | (3) |
Lemma (2-3) [9]If 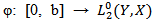 satisfies
satisfies 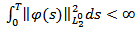 then the above sum in (3) is well defined as an X-valued random variable and we have
then the above sum in (3) is well defined as an X-valued random variable and we have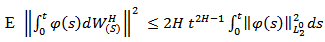 | (4) |
Definition (2-2) [15]:- The fractional integral of order 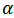 with the lower limit 0 for a function f is defined as:
with the lower limit 0 for a function f is defined as: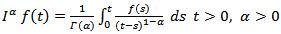 Where
Where 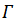 is a gamma function.Definition (2-3) [15]:- The Riemann - Liouvill derivative of order
is a gamma function.Definition (2-3) [15]:- The Riemann - Liouvill derivative of order 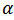 with lower zero for a function
with lower zero for a function 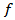 can be written as:
can be written as: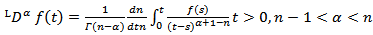 Definition (2-4) [15]:- The Laplace transform of the Riemann-Liouville fractional integral gives
Definition (2-4) [15]:- The Laplace transform of the Riemann-Liouville fractional integral gives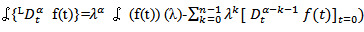
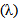 Where
Where 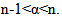 Definition (2-5) An X-valued process x(t)
Definition (2-5) An X-valued process x(t) 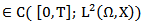 is called a mild solution of the stochastic integro-differential equation with mixed type of Brownian motion which is Wand
is called a mild solution of the stochastic integro-differential equation with mixed type of Brownian motion which is Wand 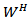 are independent in (1) If
are independent in (1) If 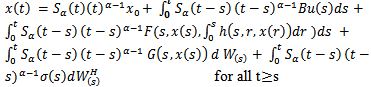 | (5) |
where 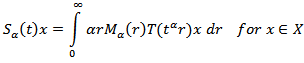
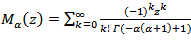 is a Mainardi's functionWhere
is a Mainardi's functionWhere 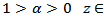 Lemma (2-4):-
Lemma (2-4):- 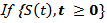 is a strongly continuous compact semigroup of bounded linear operators in X, then The operator
is a strongly continuous compact semigroup of bounded linear operators in X, then The operator 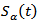 have the following properties:(i) For any fixed
have the following properties:(i) For any fixed 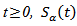 is a linear and bounded operator, i.e,
is a linear and bounded operator, i.e, 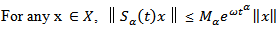 | (6) |
(ii) 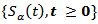 is a strongly continuous, which mean that for every
is a strongly continuous, which mean that for every 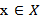 and
and 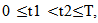 we have
we have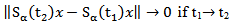 (iii) For every
(iii) For every 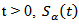 is compact operator.Proof: The proof of this lemma similar to the proof of the Lemma 3.2 (see [21]).In order to study the approximate controllability for fractional stochastic control system (1) we introduce the following linear fractional differential system corresponding to system (1)
is compact operator.Proof: The proof of this lemma similar to the proof of the Lemma 3.2 (see [21]).In order to study the approximate controllability for fractional stochastic control system (1) we introduce the following linear fractional differential system corresponding to system (1) 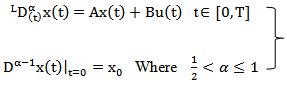 | (7) |
Definition (2-6)The set 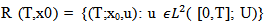 (where x(T;x0,u) the state value of the system (1) at time terminal time T corresponding to the control u and the initial value x0) is called the reachable set of system(1) at terminal time T. The closure of R (T, x0) in the space
(where x(T;x0,u) the state value of the system (1) at time terminal time T corresponding to the control u and the initial value x0) is called the reachable set of system(1) at terminal time T. The closure of R (T, x0) in the space 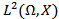 is denoted by R (T, x0).Definition (2-7) The system (1) is said to be approximately controllability on [0,T] if the reachable set R (T,x0) is dense in the space
is denoted by R (T, x0).Definition (2-7) The system (1) is said to be approximately controllability on [0,T] if the reachable set R (T,x0) is dense in the space 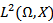 this mean that
this mean that 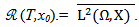 Lemma (2-5) [12] The linear fractional deterministic system (2.9) is approximately controllable on [0, T] iff the operator
Lemma (2-5) [12] The linear fractional deterministic system (2.9) is approximately controllable on [0, T] iff the operator 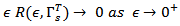 for all
for all 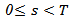 and Moreover
and Moreover 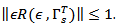 Lemma (2-6) For any
Lemma (2-6) For any 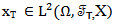 there exists
there exists 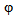
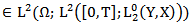 and
and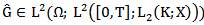 Such that
Such that 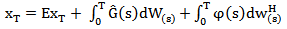 | (8) |
We Define the operator 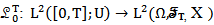 as
as 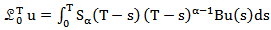 | (9) |
It is clear that 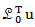 is bounded if
is bounded if 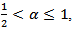 The adjoint operator
The adjoint operator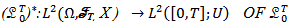 is defined by
is defined by 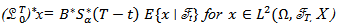 Now to defined the controllability operator
Now to defined the controllability operator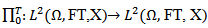 associated with (1) as
associated with (1) as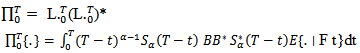 | (10) |
and the controllability operator 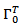 associated with(7) as
associated with(7) as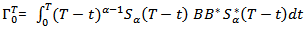 | (11) |
clearly that the operators 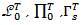 are linear bounded.For any
are linear bounded.For any 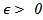 and
and 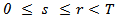 we defined the operator
we defined the operator 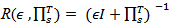 The relationship between controllability operator
The relationship between controllability operator 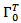 and
and 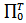 is (see [7], [12])
is (see [7], [12])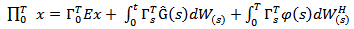 | (12) |
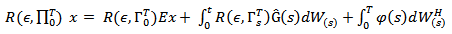 | (13) |
Definition (2-8) for any 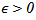 and any
and any 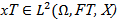 the stochastic control function of the system (2.1) in the following form:
the stochastic control function of the system (2.1) in the following form: | (14) |
3. Main Result of the Approximate Controllability
In this section, we will formulate the sufficient conditions and prove the result for the approximate controllability of nonlinear fractional stochastic system (1). For this purpose, firstly, we will prove the existence and uniqueness of solution by using the contraction mapping principle. Secondly, we shall prove in theorem 3.2, that the system in (1) is approximate controllability under certain assumptions. Now, assume that, (H1): for 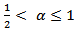 The operator
The operator 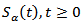 is compact and satisfies
is compact and satisfies 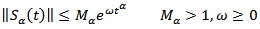 (H2) The linear fractional differential system (7) is approximately controllable on [0,T].(H3) The function
(H2) The linear fractional differential system (7) is approximately controllable on [0,T].(H3) The function 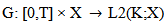 satisfies the following properties(i)
satisfies the following properties(i) 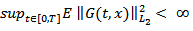 (ii)
(ii) 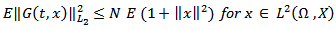 (iii) G is Lipschitz condition for all
(iii) G is Lipschitz condition for all 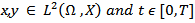 there exists
there exists 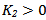 such that
such that 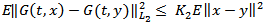 (H4) The function
(H4) The function 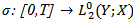 satisfies
satisfies 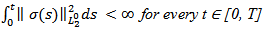 (H5) There exists a positive constant
(H5) There exists a positive constant 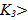 such that
such that 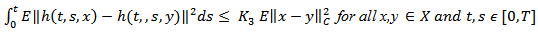 (H6)The function
(H6)The function 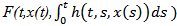 is a continuous and satisfies the usual growth condition
is a continuous and satisfies the usual growth condition 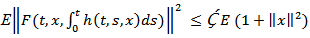 and Lipchitz condition: there exist constant
and Lipchitz condition: there exist constant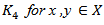
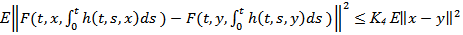 Lemma 3-1There exists positive real constants
Lemma 3-1There exists positive real constants 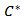 and
and 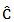 such that, for all
such that, for all 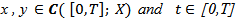
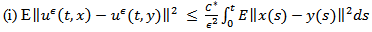 | (15) |
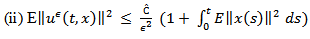 | (16) |
Proofi. Let 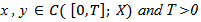 be a fixed from (14) we have
be a fixed from (14) we have 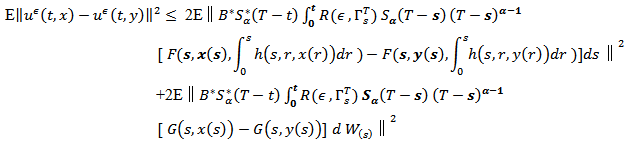 By using the
By using the 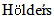 inequality, lemma 2.4, Ito isomery theorem and from lemma 2.3 we obtain
inequality, lemma 2.4, Ito isomery theorem and from lemma 2.3 we obtain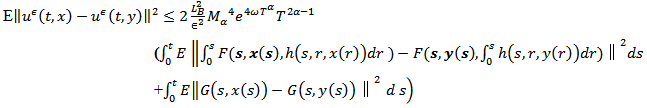 So, from the assumptions of data, we obtain
So, from the assumptions of data, we obtain 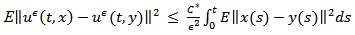 Where
Where 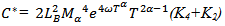 Since the proof of the second inequality can be verified in a similar manner. The proof is completed.Theorem (2-1)Assume that the conditions (H1) – (H6) are satisfied, then the system (1) has a mild solution on [0, T].Proof: For any
Since the proof of the second inequality can be verified in a similar manner. The proof is completed.Theorem (2-1)Assume that the conditions (H1) – (H6) are satisfied, then the system (1) has a mild solution on [0, T].Proof: For any 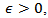 define the operator
define the operator 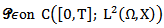 by
by 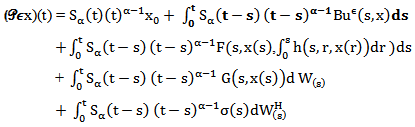 | (17) |
It will be shown that the system (1) is approximately controllable if for all 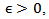 There exists a fixed point of operator
There exists a fixed point of operator 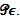 To prove this result, we use the contraction mapping principle.The proof of the theorem is long and technical, therefore it is convenient to divide it in to three steps.Step 1To prove for any
To prove this result, we use the contraction mapping principle.The proof of the theorem is long and technical, therefore it is convenient to divide it in to three steps.Step 1To prove for any 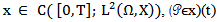 is continuous on [0,T] in
is continuous on [0,T] in 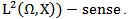 Let
Let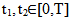 such that t1< t2. Then for any fixed
such that t1< t2. Then for any fixed 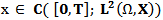 we have
we have 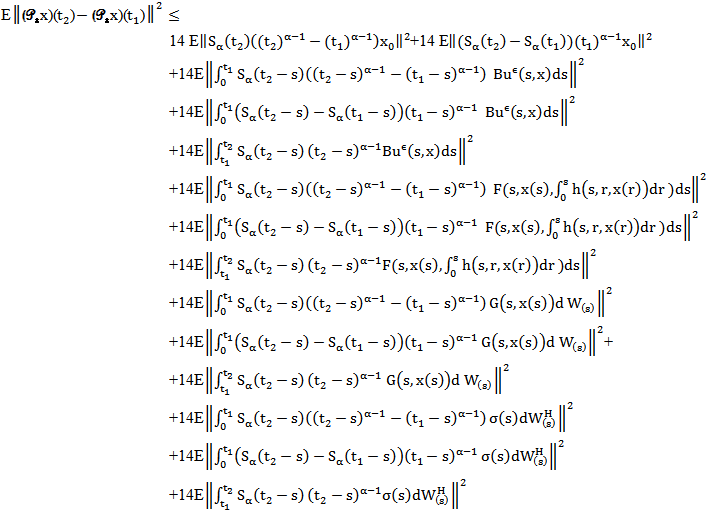 Now By using the strong continuity of a semigroup
Now By using the strong continuity of a semigroup 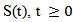 with lemma 2.4 we get
with lemma 2.4 we get 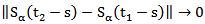 if
if 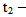
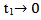 and by using Lebesgueś dominated convergence theorem , we conclude that the right –hand side of the above inequality tend to zero as
and by using Lebesgueś dominated convergence theorem , we conclude that the right –hand side of the above inequality tend to zero as 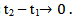 Thus we conclude
Thus we conclude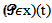 is continuous from the right in [0,T).A similar argument shows that it is also continuous from the left in (0,T].Thus
is continuous from the right in [0,T).A similar argument shows that it is also continuous from the left in (0,T].Thus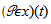 is continuous on [0,T] in
is continuous on [0,T] in 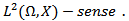 Step 2For each
Step 2For each 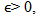 To show that the operator
To show that the operator 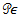 maps
maps  into itself. Let
into itself. Let 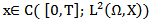
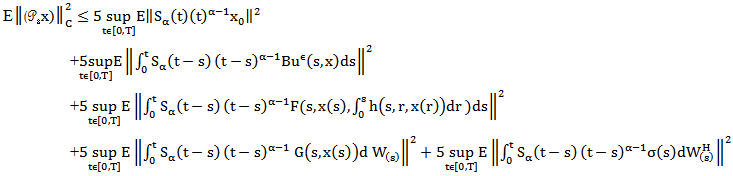 by using
by using 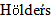 inequality, lemma 2.4, Ito isomery theorem, lemma 2.3 and assumptions H1-H6 we obtain
inequality, lemma 2.4, Ito isomery theorem, lemma 2.3 and assumptions H1-H6 we obtain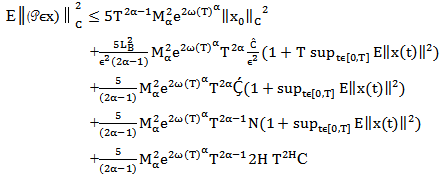 From this inequality
From this inequality  We get
We get  this mean that
this mean that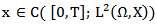 .Step 3:In both steps 1 and 2 we showed that the operator
.Step 3:In both steps 1 and 2 we showed that the operator 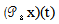 is a continuous on [0,T] and so
is a continuous on [0,T] and so 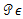 maps from
maps from 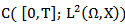 in to
in to 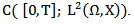 In this step we will prove the theorem through the Banach fixed point theorem that for each fixed
In this step we will prove the theorem through the Banach fixed point theorem that for each fixed 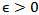 the operator
the operator 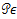 has a unique fixed point in
has a unique fixed point in 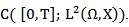 Now, we will show that
Now, we will show that 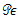 is a contraction mapping in
is a contraction mapping in 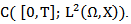 Let
Let 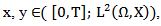 then for any fixed t ∈ [0,T] we have
then for any fixed t ∈ [0,T] we have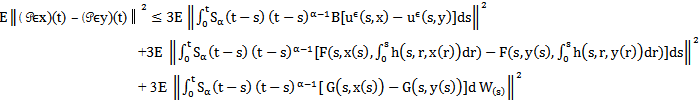 Using
Using 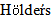 inequality, lemma 2.4, Ito isomery theorem, lemma 2.3, assumptions H1-H6 and the fact that
inequality, lemma 2.4, Ito isomery theorem, lemma 2.3, assumptions H1-H6 and the fact that 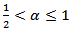 we obtain
we obtain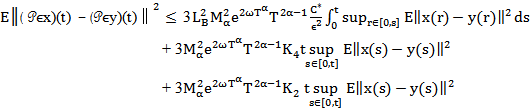 Taking the supremum over [0, T] for both sides of the above inequality, we get
Taking the supremum over [0, T] for both sides of the above inequality, we get 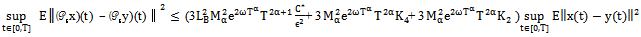 Then,
Then, 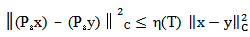 Where
Where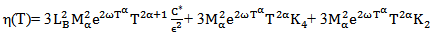 So, there exists
So, there exists 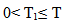 such that
such that 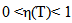 and
and 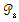 is a contraction mapping on
is a contraction mapping on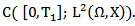 and therefore has a unique fixed point, which is a mild solution of equation 2.1 on [0, T1]. This procedure can be repeated in order to extend the solution to the entire interval [0,T] in finitely many steps. This completes the proof.Theorem (2-3)Assume the conditions (H1)-(H6) are satisfied and moreover assume that F and G are uniformly bounded. Then the system (2.1) is an approximately controllable on [0,T].Proof for every
and therefore has a unique fixed point, which is a mild solution of equation 2.1 on [0, T1]. This procedure can be repeated in order to extend the solution to the entire interval [0,T] in finitely many steps. This completes the proof.Theorem (2-3)Assume the conditions (H1)-(H6) are satisfied and moreover assume that F and G are uniformly bounded. Then the system (2.1) is an approximately controllable on [0,T].Proof for every 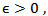 let
let 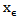 be a fixed point of the operator
be a fixed point of the operator 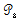 in
in  From (17) we have
From (17) we have 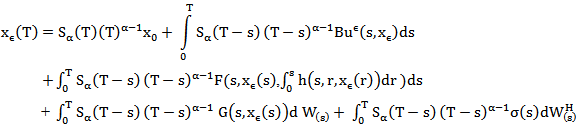 | (18) |
Using the control function in (14), the stochastic Fubini theorem and the definition of controllability operator in…(11), we obtain 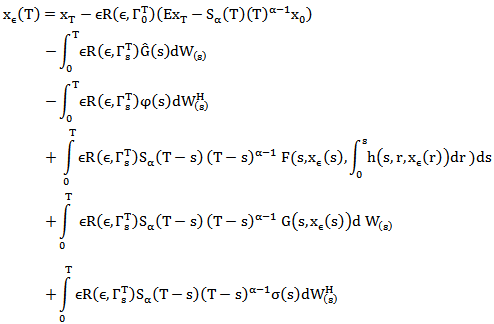 Since the functions F and G are uniformly bounded, then, there exists constants Ď1> 0 and Ď2 > 0 such that
Since the functions F and G are uniformly bounded, then, there exists constants Ď1> 0 and Ď2 > 0 such that 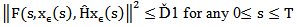 In X. and
In X. and 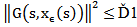 in L2(K ;X)Where
in L2(K ;X)Where 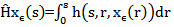 So, the sequences
So, the sequences 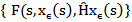 and
and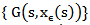 are bounded in X and L2 (K;X) respectively. Then, there are subsequences denoted by
are bounded in X and L2 (K;X) respectively. Then, there are subsequences denoted by 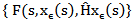 and
and 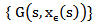 that converges weakly toF(s) in X and G(s) in L2 (K;X) respectively.Now since
that converges weakly toF(s) in X and G(s) in L2 (K;X) respectively.Now since 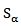 is compact by lemma 2.4 then
is compact by lemma 2.4 then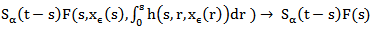 in X and
in X and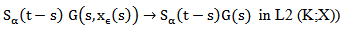 On the other hand by the assumption (H2), for all
On the other hand by the assumption (H2), for all 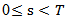 the operator
the operator 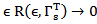 Strongly as
Strongly as 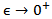 and moreover
and moreover 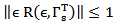 Now
Now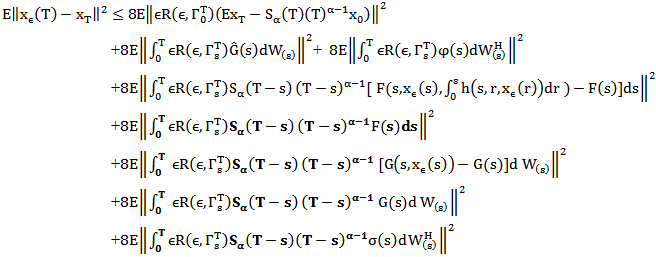 Using Ito isometry and lemma 2.3 we have
Using Ito isometry and lemma 2.3 we have 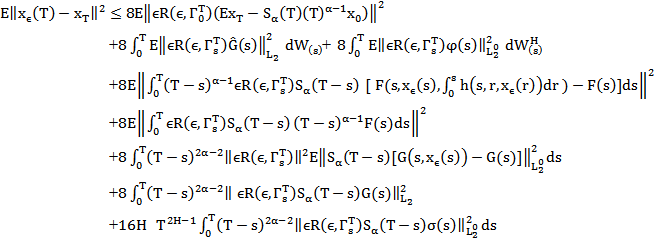 By the Lebesgue dominated convergence theorem, the compactness of
By the Lebesgue dominated convergence theorem, the compactness of 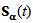 and
and 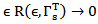 strongly as
strongly as 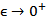 for all 0
for all 0 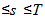 and moreover
and moreover 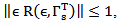 we obtain
we obtain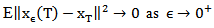 This gives the approximate controllability.
This gives the approximate controllability.
4. Illustrative Example
In this section we will take the following example as an application to theorem 2.2Consider the following control system governed by the stochastic fractional partial integro-differential equation,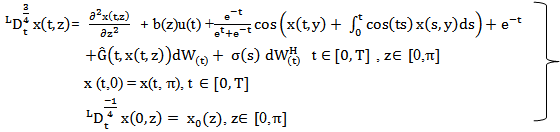 | (19) |
To study this system, let 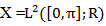 {all square integralable functions on
{all square integralable functions on 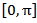 with values in real numbers R}
with values in real numbers R}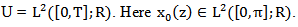
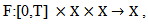
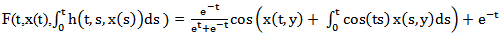 Then F is continuous and uniformly bounded function
Then F is continuous and uniformly bounded function 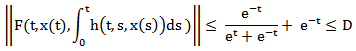 Define
Define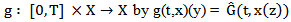 Here g is a continuous and uniformly bounded function.Let
Here g is a continuous and uniformly bounded function.Let 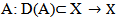 be an operator defend by A
be an operator defend by A 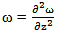 with domain
with domain 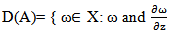 are absolutely continuous,
are absolutely continuous, 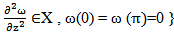 From this, A is well defined that it is infinitesimal generated of compact semi group
From this, A is well defined that it is infinitesimal generated of compact semi group 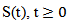 in X and it is given by S(t)
in X and it is given by S(t) 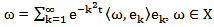 Where
Where 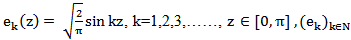 is a complete orthonormal basis in X, From this, we have
is a complete orthonormal basis in X, From this, we have 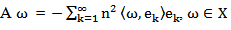 With the choice of A, F, G and h, (19) can be rewritten as the form of system (1). Thus, under the appropriate assumptions on the functions F, G, h as those in H1 –H6, system (19) is approximately controllable .
With the choice of A, F, G and h, (19) can be rewritten as the form of system (1). Thus, under the appropriate assumptions on the functions F, G, h as those in H1 –H6, system (19) is approximately controllable .
References
| [1] | Balakrishnan A. v; Applications of mathematics. springer 1976. |
| [2] | Brahim Boufoussi, On ASdedriven by a fractional Brownian motion and with onotone DRIFTElect. Comm. in Probab. 8 (2003)122{134. |
| [3] | Delia Coculescu and Ashkan Nikeghbali, FILTRATIONS, arXiv: 0712.0622v1 [math.PR] 4 Dec 2007. |
| [4] | Gani .J, T.G. Probability and Its Applications Springer-Verlag London Limited 2008. |
| [5] | Hamdy M Ahmed* Approximate controllability of impulsive neutral stochastic differential equations with fractional Brownian motion in a Hilbert space , Advances in Difference Equations 2014, 2014:113. |
| [6] | K. Balachandran, S. Karthikeyan, Controllability of stochastic integrodifferential systems, International Journal of Control, 80(2007), 486-491. |
| [7] | K. Balachandran, J.H. Kim, S. Karthikeyan, Complete controllability of stochastic integrodifferential systems, Dynamic Systems and Applications, 17(2008), 43-52. |
| [8] | Klamka, J: Stochastic controllability of linear systems with delay in control. Bull. Pol. Acad. Sci., Tech. Sci. 55(1), 23-29 (2007). |
| [9] | Kexue LI stochastic delay fractional evolution equations driven by fractional brownain motion arXiv:1406.3336vi 11 jun 2014. |
| [10] | Muthukumar and C. Rajivganthi: approximate controllability of fractional order neutral stochastic integro-differential system with nonlocal conditions and infinite delay. TIWANESE JOURNAL OF MATHEMATICS vol. 17, no.5, pp.1693-1713, October 2013. |
| [11] | N.I. Mahmudov, A. Denker, On controllability of linear stochastic systems, International Journal of Control, 73(2000), 144-151. |
| [12] | N.I. Mahmudov, Approximate controllability of semilinear deterministic and stochastic evolution equations in abstract spaces, SIAM Journal on Control and Optimization, 42(2003), 1604-1622. |
| [13] | Paul H. Bezandry , Existence of almost periodic solutions for semilinearstochastic evolution equations driven by fractional Brownian motion Electronic Journal of Differential Equations, Vol. 2012 (2012), No. 156. |
| [14] | Pazy, A: Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences, vol. 44. Springer, New York (1983). |
| [15] | Podlubny, I: Fractional Differential Equations. Academic press, san Diego (1999). |
| [16] | Sakthivel, R: Approximate controllability of impulsive stochastic evolution equations. Funkc. Ekvacioj 52, 381-393 (2009). |
| [17] | Stroock, D, W: Probability theory: an analytic view. Cambridge university press 1999. |
| [18] | Toufik Guendouzi Approximate controllability of Fractional stochastic functional evolution equations driven by A fractional Brownian motion ROMAI J., v.8, no.2(2012), 103–117. |
| [19] | Y. Mishura, Stochastic calculus for fractional Brownian motion and related processes, Springer, Berlin, 2008. |
| [20] | zang and Li; Approximate controllability of fractional impulsive neutral stochastic differential equations with nonlocal conditions , springer open journal 2013:193. |
| [21] | Zhou, Y, Jiao, F: Existence of mild solution for fractional neutral evolution equations. comput. Math. Appl.59, 1063-1077(2010). |
| [22] | Sakthivel .R and and. Mahmudov N. I, Approximate controllability of nonlinear deterministic and stochastic systems with unbounded delay , TAIWANESE JOURNAL OF MATHEMATICS Vol. 14, No. 5, pp. 1777-1797, October 2010. |

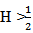 and wiener process in real separable Hilbert space. An example was stated as a application of our result.
and wiener process in real separable Hilbert space. An example was stated as a application of our result.
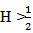 and wiener process. The following form is the system under our consideration,
and wiener process. The following form is the system under our consideration,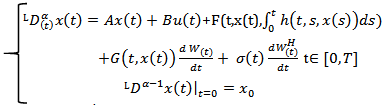
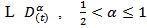 the Riemann-Liouville fractional derivative of order α. A: Dom(A) ⊂ X →X is the infinitesimal generator of strongly continuous compact semi group of bounded linear operators
the Riemann-Liouville fractional derivative of order α. A: Dom(A) ⊂ X →X is the infinitesimal generator of strongly continuous compact semi group of bounded linear operators 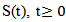 in X. x(.) takes the value in the real separable Hilbert space X such that for each
in X. x(.) takes the value in the real separable Hilbert space X such that for each ,
, 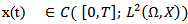
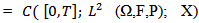 the banach space of all continuous functions from [0,T] in to
the banach space of all continuous functions from [0,T] in to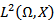 satisfying the condition
satisfying the condition 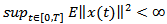 and
and 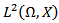 is a banach space of all F-measurable square integrable random variables with values in Hilbert space X equipped with the sup norm
is a banach space of all F-measurable square integrable random variables with values in Hilbert space X equipped with the sup norm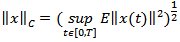
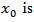 F0 –measurable X- valued random variable independent of W and
F0 –measurable X- valued random variable independent of W and 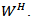
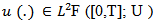 is the space of the Ft – adapted , U-valued measurable process u(t) on [0,T] such that
is the space of the Ft – adapted , U-valued measurable process u(t) on [0,T] such that 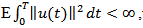 with norm
with norm 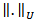 where U is a real separable Hilbert space. B is the linear bounded operator from U into X such that there exists constant
where U is a real separable Hilbert space. B is the linear bounded operator from U into X such that there exists constant 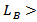
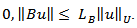
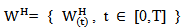 is a Q-fractional Brownian motion with Hurst index
is a Q-fractional Brownian motion with Hurst index 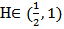 defined in a complete probability space
defined in a complete probability space 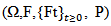 with values in a Hilbert space Y.
with values in a Hilbert space Y.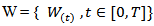 is a Q-l wiener process defined on
is a Q-l wiener process defined on 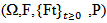 with values in a Hilbert space K.
with values in a Hilbert space K.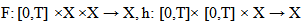 and
and 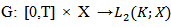 are continuous functions and uniformly bounded.
are continuous functions and uniformly bounded. 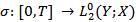 is a deterministic function the processes W and
is a deterministic function the processes W and 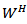 are independent.In the past few decades, the theory of fractional partial differential equations in both types deterministic and stochastic, have received a great deal of attention and play an important role in many applied scientific fields.The deterministic models often affected due to fractal noise, which is random or at least appears to be so. Therefore, the study of stochastic systems are more applicable in dynamical system theory. Random phenomena exist everywhere in the real world. Systems are often.Subjected to random perturbations. The existence of solution for some classes of Stochastic equations driven by fractional Brownian motion have been investigated by many authors, see, for example [4], [9], [19].The controllability of stochastic differential equations in infinite dimensional spaces have been investigated by many authors [6], [7], [8], [11], [12]. In recent years, sakthivel [15] derived a set of sufficient conditions for approximate controllability of nonlinear impulsive stochastic differential equations in a real separable Hilbert space by using the stochastic analysis theory and a fixed point. Zang and Li [20] studied the approximate controllability of fractional impulsive neutral stochastic differential equations with non-local conditions and infinite delay in Hilbert space. Guendouzi [18] studies the approximate controllability result of a class of dynamic control systems described by nonlinear fractional stochastic functional differential equations in Hilbert.Space driven by a fractional Brownian motion with Hurst parameter H > 1/2 by using the theory of fractional calculus and a fixed point theorm. Hamdy [5] studied the approximate controllability for impulsive neutral stochastic functional differential equations with finite delay and fractional Brownian motion in a Hilbert space by using semigroup theory, stochastic analysis, and Banach’s fixed point theorem.In this paper we will study the approximate controllability of nonlinear stochastic system. More precisely, we shall formulate and prove sufficient conditions for the Approximate controllability of fractional stochastic integro-differential equations driven by mixed type of fractional Brownian motion with Hurst
are independent.In the past few decades, the theory of fractional partial differential equations in both types deterministic and stochastic, have received a great deal of attention and play an important role in many applied scientific fields.The deterministic models often affected due to fractal noise, which is random or at least appears to be so. Therefore, the study of stochastic systems are more applicable in dynamical system theory. Random phenomena exist everywhere in the real world. Systems are often.Subjected to random perturbations. The existence of solution for some classes of Stochastic equations driven by fractional Brownian motion have been investigated by many authors, see, for example [4], [9], [19].The controllability of stochastic differential equations in infinite dimensional spaces have been investigated by many authors [6], [7], [8], [11], [12]. In recent years, sakthivel [15] derived a set of sufficient conditions for approximate controllability of nonlinear impulsive stochastic differential equations in a real separable Hilbert space by using the stochastic analysis theory and a fixed point. Zang and Li [20] studied the approximate controllability of fractional impulsive neutral stochastic differential equations with non-local conditions and infinite delay in Hilbert space. Guendouzi [18] studies the approximate controllability result of a class of dynamic control systems described by nonlinear fractional stochastic functional differential equations in Hilbert.Space driven by a fractional Brownian motion with Hurst parameter H > 1/2 by using the theory of fractional calculus and a fixed point theorm. Hamdy [5] studied the approximate controllability for impulsive neutral stochastic functional differential equations with finite delay and fractional Brownian motion in a Hilbert space by using semigroup theory, stochastic analysis, and Banach’s fixed point theorem.In this paper we will study the approximate controllability of nonlinear stochastic system. More precisely, we shall formulate and prove sufficient conditions for the Approximate controllability of fractional stochastic integro-differential equations driven by mixed type of fractional Brownian motion with Hurst 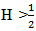 and wiener process in Hilbert space. The rest of this paper is organized as follows, in section 2, we will introduced some concepts, definitions and some lemmas of fractional stochastic calculus which are useful for us here. In section 3, we will prove our main result. Finally in section 4, as an application, an example will be stated in details.
and wiener process in Hilbert space. The rest of this paper is organized as follows, in section 2, we will introduced some concepts, definitions and some lemmas of fractional stochastic calculus which are useful for us here. In section 3, we will prove our main result. Finally in section 4, as an application, an example will be stated in details.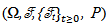 be a complete probability space with natural filtration
be a complete probability space with natural filtration 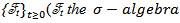 generated by therandom variables
generated by therandom variables 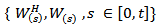 and the P-null set). We denote by L (K; X) the space of all bounded linear operators from K to X and L(Y; X) denote the space of all bounded linear operators from Y to X. For convenience we will use the same notation
and the P-null set). We denote by L (K; X) the space of all bounded linear operators from K to X and L(Y; X) denote the space of all bounded linear operators from Y to X. For convenience we will use the same notation 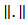 to denote the norms in K, Y, X,L (K;X), L(Y;X) and use
to denote the norms in K, Y, X,L (K;X), L(Y;X) and use 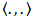 to the inner product of K , Y , X.Definition (2.1) [1]:A standard fractional Brownian motion with Hurst index H ∈ (0,1) is a Gaussian process
to the inner product of K , Y , X.Definition (2.1) [1]:A standard fractional Brownian motion with Hurst index H ∈ (0,1) is a Gaussian process 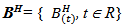 on (Ω, F, P) having the properties i.
on (Ω, F, P) having the properties i. 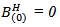 ii.
ii. 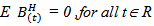 iii.
iii. 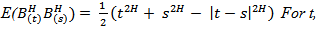
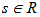 If
If 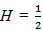 Then the increments of BH are non-correlated, and consequently independent. So BH is a standard Wiener Process which we denote further by B.-If H
Then the increments of BH are non-correlated, and consequently independent. So BH is a standard Wiener Process which we denote further by B.-If H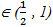 then the increments are positively correlated-If H
then the increments are positively correlated-If H 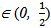 then the increments are negative correlatedMoreover, BH has the integral representation
then the increments are negative correlatedMoreover, BH has the integral representation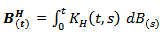 Where B is a standard Wiener process and the kernel
Where B is a standard Wiener process and the kernel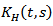 defined as
defined as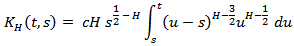 and
and 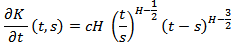
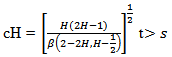 in the case
in the case 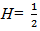 we shall use Ito Isometry
we shall use Ito Isometry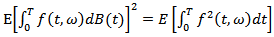
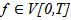 the class of functions such that
the class of functions such that 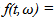
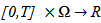 and f is measurable,
and f is measurable, 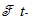 adapted and
adapted and 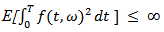 Suppose
Suppose 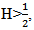 We denote by the set of step functions on [0, T]The integral of Φ∈ᶓ with respect to a standard fractional Brownian motion will be defined by,
We denote by the set of step functions on [0, T]The integral of Φ∈ᶓ with respect to a standard fractional Brownian motion will be defined by,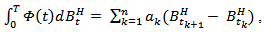 Where
Where 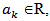
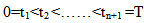 NOW, Let
NOW, Let 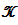 be the Hilbert space defined as the closure of ᶓ with respect to the scalar product
be the Hilbert space defined as the closure of ᶓ with respect to the scalar product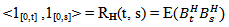 The mapping
The mapping 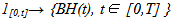 can be extended to an isometry between H and
can be extended to an isometry between H and 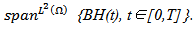 Let │H│ be the Banach space of measurable functions ' on [0, T], such that
Let │H│ be the Banach space of measurable functions ' on [0, T], such that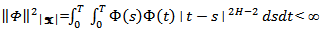 Lemma (2-1) [9]
Lemma (2-1) [9]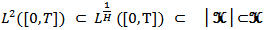 and for any
and for any 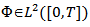 we have
we have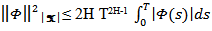 Now Suppose that there exists a complete orthonormal system
Now Suppose that there exists a complete orthonormal system 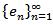 in Y. Let
in Y. Let 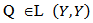 be the operator defined by
be the operator defined by 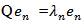 where
where 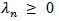 (n=1,2,….) are non-negative real numbers .With finite trace.Tr
(n=1,2,….) are non-negative real numbers .With finite trace.Tr 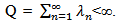 Analogically to Wiener processes in a Hilbert space, we defined A fractional Brwnian Motion on Y by using covariance operator Q as
Analogically to Wiener processes in a Hilbert space, we defined A fractional Brwnian Motion on Y by using covariance operator Q as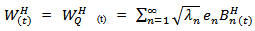 Where
Where 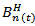 are standard fractional Brownian motions mutually independent on
are standard fractional Brownian motions mutually independent on 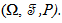 In order to defined stochastic integral with respect to the Q-fractional Brownian motion.We introduce the space
In order to defined stochastic integral with respect to the Q-fractional Brownian motion.We introduce the space 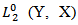 of all Q-Hilbert- Schmidt operators that is with the inner product
of all Q-Hilbert- Schmidt operators that is with the inner product 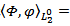
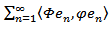 is a separable Hilbert space. L2(K;X) the space of all Hilbert-Schmidt operators acting between K and X equipped with the Hilbert-Schmidt norm
is a separable Hilbert space. L2(K;X) the space of all Hilbert-Schmidt operators acting between K and X equipped with the Hilbert-Schmidt norm 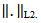 Lemma (2-2)Let
Lemma (2-2)Let 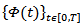 be a deterministic function with values in
be a deterministic function with values in 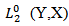 The stochastic integral of Φ with respect to
The stochastic integral of Φ with respect to 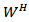 is defined by
is defined by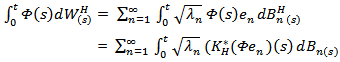
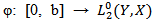 satisfies
satisfies 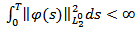 then the above sum in (3) is well defined as an X-valued random variable and we have
then the above sum in (3) is well defined as an X-valued random variable and we have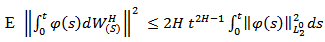
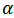 with the lower limit 0 for a function f is defined as:
with the lower limit 0 for a function f is defined as: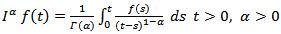 Where
Where 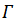 is a gamma function.Definition (2-3) [15]:- The Riemann - Liouvill derivative of order
is a gamma function.Definition (2-3) [15]:- The Riemann - Liouvill derivative of order 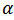 with lower zero for a function
with lower zero for a function 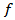 can be written as:
can be written as: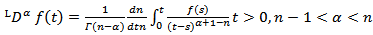 Definition (2-4) [15]:- The Laplace transform of the Riemann-Liouville fractional integral gives
Definition (2-4) [15]:- The Laplace transform of the Riemann-Liouville fractional integral gives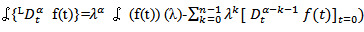
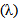 Where
Where 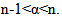 Definition (2-5) An X-valued process x(t)
Definition (2-5) An X-valued process x(t) 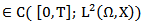 is called a mild solution of the stochastic integro-differential equation with mixed type of Brownian motion which is Wand
is called a mild solution of the stochastic integro-differential equation with mixed type of Brownian motion which is Wand 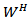 are independent in (1) If
are independent in (1) If 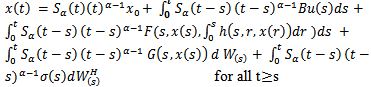
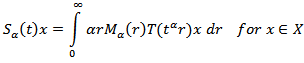
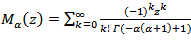 is a Mainardi's functionWhere
is a Mainardi's functionWhere 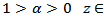 Lemma (2-4):-
Lemma (2-4):- 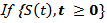 is a strongly continuous compact semigroup of bounded linear operators in X, then The operator
is a strongly continuous compact semigroup of bounded linear operators in X, then The operator 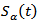 have the following properties:(i) For any fixed
have the following properties:(i) For any fixed 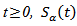 is a linear and bounded operator, i.e,
is a linear and bounded operator, i.e, 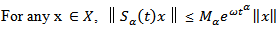
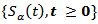 is a strongly continuous, which mean that for every
is a strongly continuous, which mean that for every 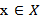 and
and 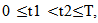 we have
we have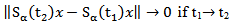 (iii) For every
(iii) For every 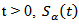 is compact operator.Proof: The proof of this lemma similar to the proof of the Lemma 3.2 (see [21]).In order to study the approximate controllability for fractional stochastic control system (1) we introduce the following linear fractional differential system corresponding to system (1)
is compact operator.Proof: The proof of this lemma similar to the proof of the Lemma 3.2 (see [21]).In order to study the approximate controllability for fractional stochastic control system (1) we introduce the following linear fractional differential system corresponding to system (1) 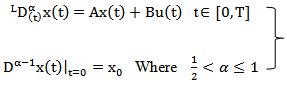
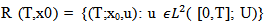 (where x(T;x0,u) the state value of the system (1) at time terminal time T corresponding to the control u and the initial value x0) is called the reachable set of system(1) at terminal time T. The closure of R (T, x0) in the space
(where x(T;x0,u) the state value of the system (1) at time terminal time T corresponding to the control u and the initial value x0) is called the reachable set of system(1) at terminal time T. The closure of R (T, x0) in the space 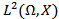 is denoted by R (T, x0).Definition (2-7) The system (1) is said to be approximately controllability on [0,T] if the reachable set R (T,x0) is dense in the space
is denoted by R (T, x0).Definition (2-7) The system (1) is said to be approximately controllability on [0,T] if the reachable set R (T,x0) is dense in the space 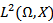 this mean that
this mean that 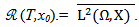 Lemma (2-5) [12] The linear fractional deterministic system (2.9) is approximately controllable on [0, T] iff the operator
Lemma (2-5) [12] The linear fractional deterministic system (2.9) is approximately controllable on [0, T] iff the operator 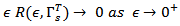 for all
for all 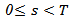 and Moreover
and Moreover 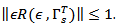 Lemma (2-6) For any
Lemma (2-6) For any 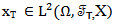 there exists
there exists 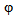
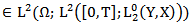 and
and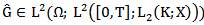 Such that
Such that 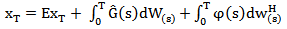
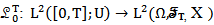 as
as 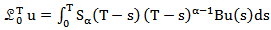
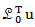 is bounded if
is bounded if 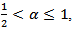 The adjoint operator
The adjoint operator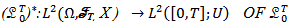 is defined by
is defined by 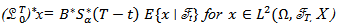 Now to defined the controllability operator
Now to defined the controllability operator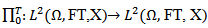 associated with (1) as
associated with (1) as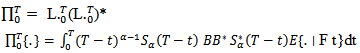
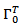 associated with(7) as
associated with(7) as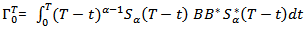
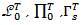 are linear bounded.For any
are linear bounded.For any 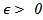 and
and 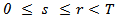 we defined the operator
we defined the operator 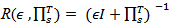 The relationship between controllability operator
The relationship between controllability operator 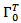 and
and 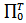 is (see [7], [12])
is (see [7], [12])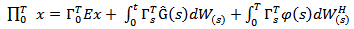
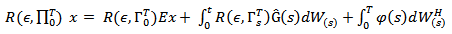
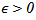 and any
and any 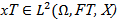 the stochastic control function of the system (2.1) in the following form:
the stochastic control function of the system (2.1) in the following form:
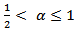 The operator
The operator 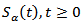 is compact and satisfies
is compact and satisfies 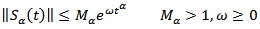 (H2) The linear fractional differential system (7) is approximately controllable on [0,T].(H3) The function
(H2) The linear fractional differential system (7) is approximately controllable on [0,T].(H3) The function 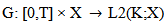 satisfies the following properties(i)
satisfies the following properties(i) 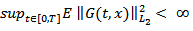 (ii)
(ii) 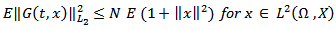 (iii) G is Lipschitz condition for all
(iii) G is Lipschitz condition for all 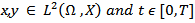 there exists
there exists 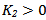 such that
such that 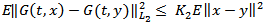 (H4) The function
(H4) The function 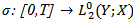 satisfies
satisfies 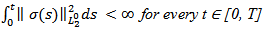 (H5) There exists a positive constant
(H5) There exists a positive constant 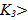 such that
such that 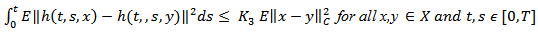 (H6)The function
(H6)The function 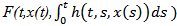 is a continuous and satisfies the usual growth condition
is a continuous and satisfies the usual growth condition 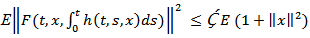 and Lipchitz condition: there exist constant
and Lipchitz condition: there exist constant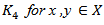
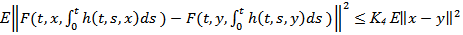 Lemma 3-1There exists positive real constants
Lemma 3-1There exists positive real constants 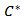 and
and 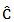 such that, for all
such that, for all 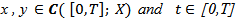
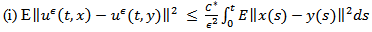
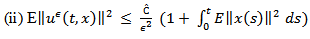
 be a fixed from (14) we have
be a fixed from (14) we have 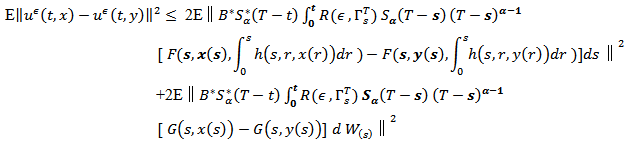 By using the
By using the 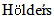 inequality, lemma 2.4, Ito isomery theorem and from lemma 2.3 we obtain
inequality, lemma 2.4, Ito isomery theorem and from lemma 2.3 we obtain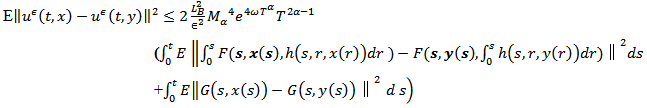 So, from the assumptions of data, we obtain
So, from the assumptions of data, we obtain 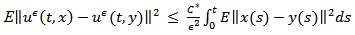 Where
Where 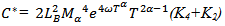 Since the proof of the second inequality can be verified in a similar manner. The proof is completed.Theorem (2-1)Assume that the conditions (H1) – (H6) are satisfied, then the system (1) has a mild solution on [0, T].Proof: For any
Since the proof of the second inequality can be verified in a similar manner. The proof is completed.Theorem (2-1)Assume that the conditions (H1) – (H6) are satisfied, then the system (1) has a mild solution on [0, T].Proof: For any 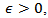 define the operator
define the operator 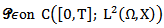 by
by 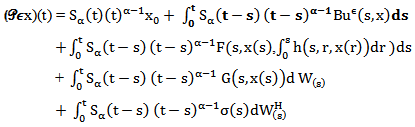
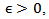 There exists a fixed point of operator
There exists a fixed point of operator 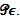 To prove this result, we use the contraction mapping principle.The proof of the theorem is long and technical, therefore it is convenient to divide it in to three steps.Step 1To prove for any
To prove this result, we use the contraction mapping principle.The proof of the theorem is long and technical, therefore it is convenient to divide it in to three steps.Step 1To prove for any 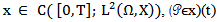 is continuous on [0,T] in
is continuous on [0,T] in 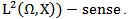 Let
Let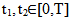 such that t1< t2. Then for any fixed
such that t1< t2. Then for any fixed 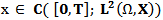 we have
we have 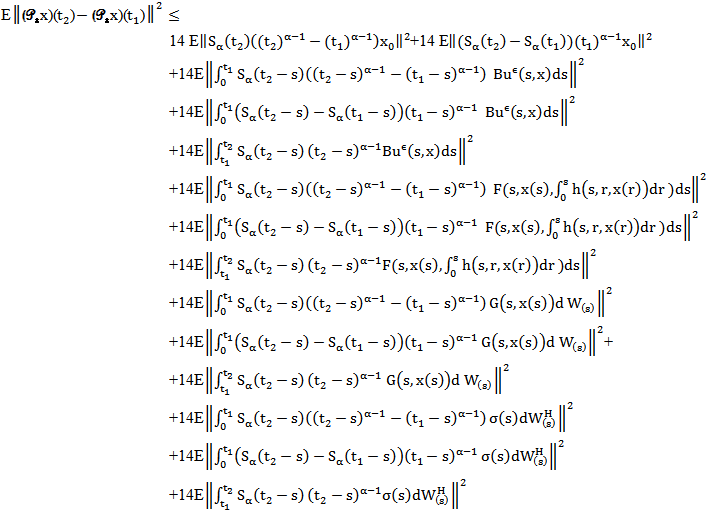 Now By using the strong continuity of a semigroup
Now By using the strong continuity of a semigroup 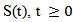 with lemma 2.4 we get
with lemma 2.4 we get 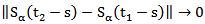 if
if 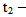
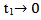 and by using Lebesgueś dominated convergence theorem , we conclude that the right –hand side of the above inequality tend to zero as
and by using Lebesgueś dominated convergence theorem , we conclude that the right –hand side of the above inequality tend to zero as 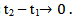 Thus we conclude
Thus we conclude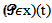 is continuous from the right in [0,T).A similar argument shows that it is also continuous from the left in (0,T].Thus
is continuous from the right in [0,T).A similar argument shows that it is also continuous from the left in (0,T].Thus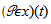 is continuous on [0,T] in
is continuous on [0,T] in 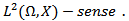 Step 2For each
Step 2For each 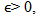 To show that the operator
To show that the operator 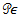 maps
maps  into itself. Let
into itself. Let 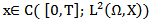
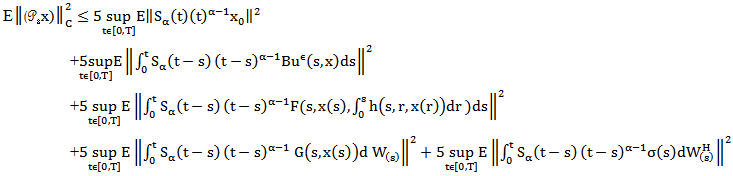 by using
by using 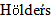 inequality, lemma 2.4, Ito isomery theorem, lemma 2.3 and assumptions H1-H6 we obtain
inequality, lemma 2.4, Ito isomery theorem, lemma 2.3 and assumptions H1-H6 we obtain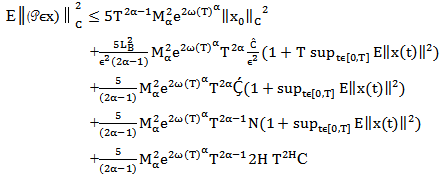 From this inequality
From this inequality 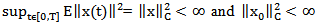 We get
We get 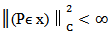 this mean that
this mean that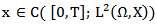 .Step 3:In both steps 1 and 2 we showed that the operator
.Step 3:In both steps 1 and 2 we showed that the operator 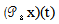 is a continuous on [0,T] and so
is a continuous on [0,T] and so 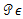 maps from
maps from 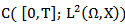 in to
in to 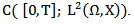 In this step we will prove the theorem through the Banach fixed point theorem that for each fixed
In this step we will prove the theorem through the Banach fixed point theorem that for each fixed 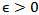 the operator
the operator 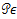 has a unique fixed point in
has a unique fixed point in 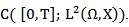 Now, we will show that
Now, we will show that 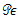 is a contraction mapping in
is a contraction mapping in 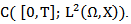 Let
Let 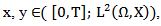 then for any fixed t ∈ [0,T] we have
then for any fixed t ∈ [0,T] we have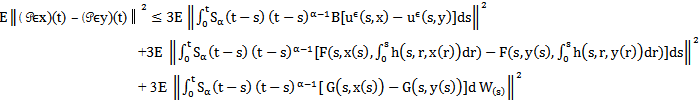 Using
Using 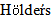 inequality, lemma 2.4, Ito isomery theorem, lemma 2.3, assumptions H1-H6 and the fact that
inequality, lemma 2.4, Ito isomery theorem, lemma 2.3, assumptions H1-H6 and the fact that 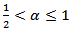 we obtain
we obtain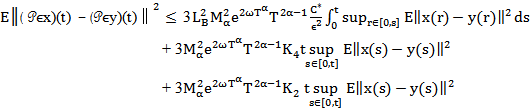 Taking the supremum over [0, T] for both sides of the above inequality, we get
Taking the supremum over [0, T] for both sides of the above inequality, we get 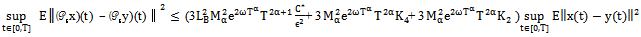 Then,
Then, 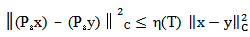 Where
Where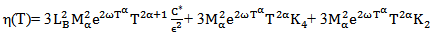 So, there exists
So, there exists 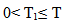 such that
such that 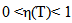 and
and 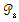 is a contraction mapping on
is a contraction mapping on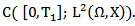 and therefore has a unique fixed point, which is a mild solution of equation 2.1 on [0, T1]. This procedure can be repeated in order to extend the solution to the entire interval [0,T] in finitely many steps. This completes the proof.Theorem (2-3)Assume the conditions (H1)-(H6) are satisfied and moreover assume that F and G are uniformly bounded. Then the system (2.1) is an approximately controllable on [0,T].Proof for every
and therefore has a unique fixed point, which is a mild solution of equation 2.1 on [0, T1]. This procedure can be repeated in order to extend the solution to the entire interval [0,T] in finitely many steps. This completes the proof.Theorem (2-3)Assume the conditions (H1)-(H6) are satisfied and moreover assume that F and G are uniformly bounded. Then the system (2.1) is an approximately controllable on [0,T].Proof for every 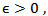 let
let 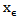 be a fixed point of the operator
be a fixed point of the operator 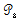 in
in 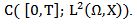 From (17) we have
From (17) we have 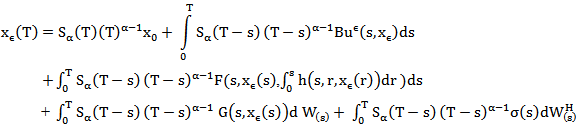
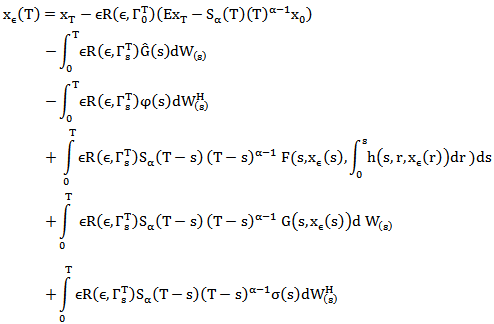 Since the functions F and G are uniformly bounded, then, there exists constants Ď1> 0 and Ď2 > 0 such that
Since the functions F and G are uniformly bounded, then, there exists constants Ď1> 0 and Ď2 > 0 such that 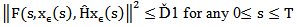 In X. and
In X. and 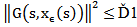 in L2(K ;X)Where
in L2(K ;X)Where 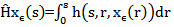 So, the sequences
So, the sequences 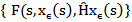 and
and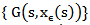 are bounded in X and L2 (K;X) respectively. Then, there are subsequences denoted by
are bounded in X and L2 (K;X) respectively. Then, there are subsequences denoted by 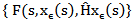 and
and 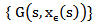 that converges weakly toF(s) in X and G(s) in L2 (K;X) respectively.Now since
that converges weakly toF(s) in X and G(s) in L2 (K;X) respectively.Now since 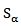 is compact by lemma 2.4 then
is compact by lemma 2.4 then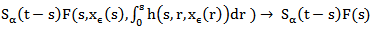 in X and
in X and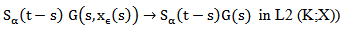 On the other hand by the assumption (H2), for all
On the other hand by the assumption (H2), for all 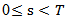 the operator
the operator 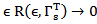 Strongly as
Strongly as 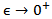 and moreover
and moreover 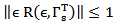 Now
Now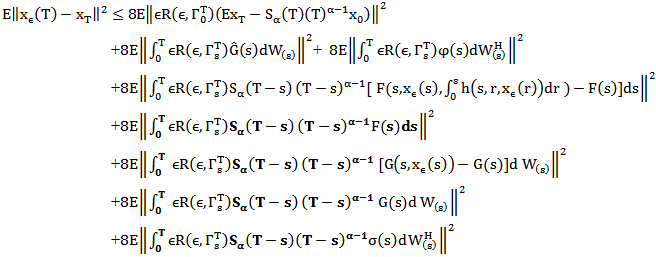 Using Ito isometry and lemma 2.3 we have
Using Ito isometry and lemma 2.3 we have 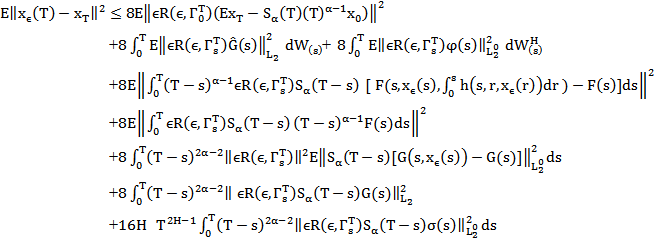 By the Lebesgue dominated convergence theorem, the compactness of
By the Lebesgue dominated convergence theorem, the compactness of 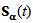 and
and 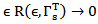 strongly as
strongly as 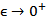 for all 0
for all 0 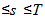 and moreover
and moreover 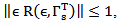 we obtain
we obtain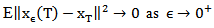 This gives the approximate controllability.
This gives the approximate controllability.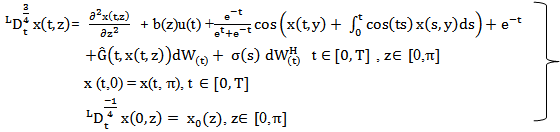
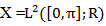 {all square integralable functions on
{all square integralable functions on  with values in real numbers R}
with values in real numbers R}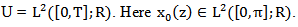
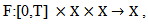
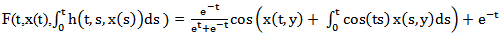 Then F is continuous and uniformly bounded function
Then F is continuous and uniformly bounded function 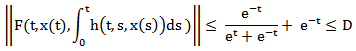 Define
Define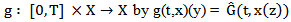 Here g is a continuous and uniformly bounded function.Let
Here g is a continuous and uniformly bounded function.Let 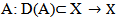 be an operator defend by A
be an operator defend by A 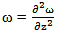 with domain
with domain 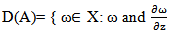 are absolutely continuous,
are absolutely continuous, 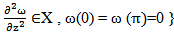 From this, A is well defined that it is infinitesimal generated of compact semi group
From this, A is well defined that it is infinitesimal generated of compact semi group 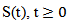 in X and it is given by S(t)
in X and it is given by S(t) 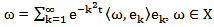 Where
Where 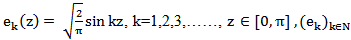 is a complete orthonormal basis in X, From this, we have
is a complete orthonormal basis in X, From this, we have 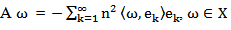 With the choice of A, F, G and h, (19) can be rewritten as the form of system (1). Thus, under the appropriate assumptions on the functions F, G, h as those in H1 –H6, system (19) is approximately controllable .
With the choice of A, F, G and h, (19) can be rewritten as the form of system (1). Thus, under the appropriate assumptions on the functions F, G, h as those in H1 –H6, system (19) is approximately controllable . Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML