Rahim M. Rzaev 1, 2, Aygun A. Abdullayeva 1
1Institute of Mathematics and Mechanics of National Academy of Sciences of Azerbaijan, Baku, Azerbaijan
2Azerbaijan State Pedagogical University, Baku, Azerbaijan
Correspondence to: Rahim M. Rzaev , Institute of Mathematics and Mechanics of National Academy of Sciences of Azerbaijan, Baku, Azerbaijan.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper is devoted to the study of certain generalized maximal function (Φ-maximal function) measuring smoothness. In this work we essentially use the relation between maximal function measuring smoothness and oscillation of functions.
Keywords:
Maximal functions, Smoothness of functions, Mean oscillation, Harmonic oscillation, Φ-oscillation
Cite this paper: Rahim M. Rzaev , Aygun A. Abdullayeva , Φ - maximal Functions Measuring Smoothness, American Journal of Mathematics and Statistics, Vol. 5 No. 2, 2015, pp. 52-59. doi: 10.5923/j.ajms.20150502.02.
1. Introduction
Let 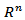 be
be 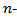 dimensional Euclidean space,
dimensional Euclidean space, 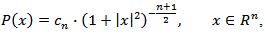
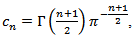
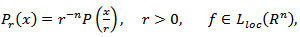
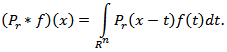 Note that the quantity
Note that the quantity 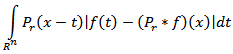 is called harmonic oscillation (see, for instance, [1], [2]). In work [2] it has proven that
is called harmonic oscillation (see, for instance, [1], [2]). In work [2] it has proven that 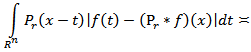
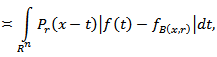 where
where 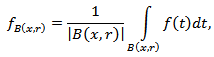
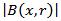 denotes the volume of ball
denotes the volume of ball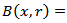
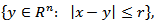 and constants in the relation
and constants in the relation 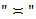 depend only on dimension
depend only on dimension 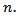 (For positive functions
(For positive functions 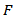 and
and 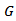 we will use the notation
we will use the notation 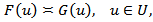 if there exist positive constants
if there exist positive constants 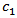 and
and 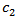 such that
such that 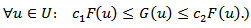 Let
Let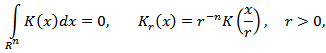
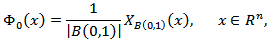 where
where 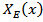 is a characteristic function of the set
is a characteristic function of the set 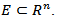 It is easy to see that
It is easy to see that 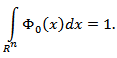 In the papers of some other authors (see e.g. [3], [4]) the quantity
In the papers of some other authors (see e.g. [3], [4]) the quantity 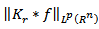 is chosen as a characteristic to determine homogeneous classes of Besov. We can write the quantity
is chosen as a characteristic to determine homogeneous classes of Besov. We can write the quantity 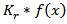 in the following form
in the following form 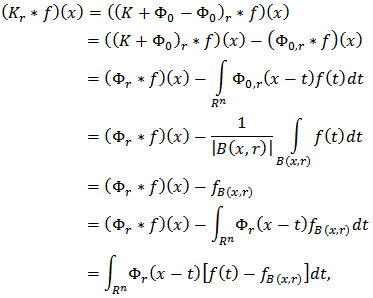 where
where 
 It is obvious that
It is obvious that 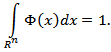 Thus,
Thus, 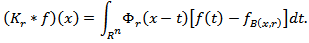 Hence we have
Hence we have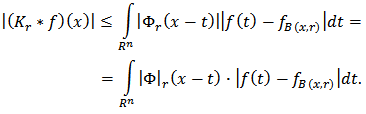 In the present paper, for the principal characteristic we take the quantity
In the present paper, for the principal characteristic we take the quantity 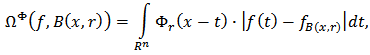 where
where 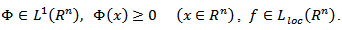
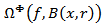 is said to be
is said to be 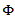 -oscillation of the function
-oscillation of the function 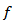 in the ball
in the ball 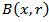 [2]. It is known that maximal functions measuring smoothness play an important role in the study of properties of integral operators and other objects of Harmonic Analysis. The main topic of this paper is the study of certain generalized maximal function (
[2]. It is known that maximal functions measuring smoothness play an important role in the study of properties of integral operators and other objects of Harmonic Analysis. The main topic of this paper is the study of certain generalized maximal function (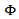 -maximal function) measuring smoothness. The paper is organized as follows. Section 2 has auxiliary character and presents the basic definitions, some notation and well-known facts. In section 3 the relations between maximal function and metric characteristic are investigated and some useful inequalities were obtained. In section 4 estimations between
-maximal function) measuring smoothness. The paper is organized as follows. Section 2 has auxiliary character and presents the basic definitions, some notation and well-known facts. In section 3 the relations between maximal function and metric characteristic are investigated and some useful inequalities were obtained. In section 4 estimations between 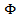 -maximal function and maximal function was obtained. The main results are given in Propositions 3.1, 3.3, 4.1, 4.3 and 4.4.
-maximal function and maximal function was obtained. The main results are given in Propositions 3.1, 3.3, 4.1, 4.3 and 4.4.
2. Some Definition and Auxiliary Facts
Let the function 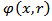 be defined on the set
be defined on the set 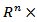
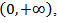 takes only positive values, and monotone increases with respect to the argument
takes only positive values, and monotone increases with respect to the argument 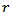 on the interval
on the interval 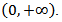 We denote the class of all functions
We denote the class of all functions 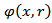 with the above mentioned properties by
with the above mentioned properties by 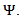 Let
Let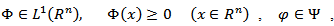
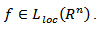 Let’s introduce the following Φ-maximal function
Let’s introduce the following Φ-maximal function 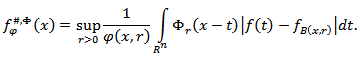 We also introduce the following metric Φ-characteristic
We also introduce the following metric Φ-characteristic 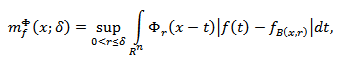
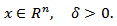 Consider the known special cases of the introduced maximal function
Consider the known special cases of the introduced maximal function 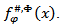 1) If
1) If 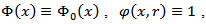 then
then 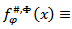
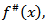 where
where 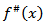 is the maximal function which is introduced in the paper [5]. 2) If
is the maximal function which is introduced in the paper [5]. 2) If 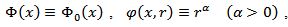 then
then 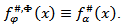 The maximal function
The maximal function 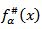 was mentioned in the papers [6], [7]. In paper [8] the function
was mentioned in the papers [6], [7]. In paper [8] the function 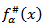 was investigated. 3) If
was investigated. 3) If 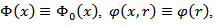 then the maximal function
then the maximal function 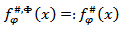 may be found in the papers [9], [10], [11], [12], [13] and others. Now let’s consider special cases of metric Φ-characteristic
may be found in the papers [9], [10], [11], [12], [13] and others. Now let’s consider special cases of metric Φ-characteristic 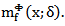 1) If
1) If 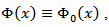 then
then 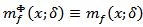 (see section 3), where
(see section 3), where 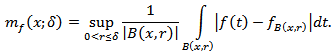 Note that the function
Note that the function 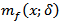 was first introduced in the paper [14] (see also, [15], [16]). 2) Let
was first introduced in the paper [14] (see also, [15], [16]). 2) Let 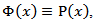 where
where 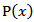 is the Poisson kernel, i.e.
is the Poisson kernel, i.e. 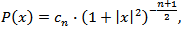 where
where 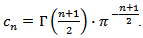 Global variant of the characteristic
Global variant of the characteristic 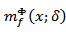 (more precisely, the equivalent characteristic to it which is called a modulus of harmonic oscillation) for periodic functions of one variable may be found in the paper [1]. It is known that Hardy-Littlewood’s maximal function is determined by the equality
(more precisely, the equivalent characteristic to it which is called a modulus of harmonic oscillation) for periodic functions of one variable may be found in the paper [1]. It is known that Hardy-Littlewood’s maximal function is determined by the equality 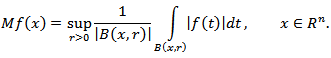 For case of
For case of 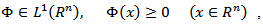
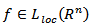 the following maximal function is also considered [17]
the following maximal function is also considered [17]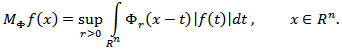 It is easy to see that if
It is easy to see that if 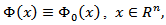 then
then 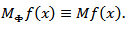 From the definition of a maximal function
From the definition of a maximal function 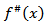 it follows that
it follows that 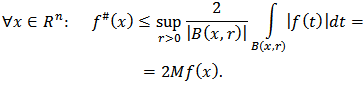 Thus,
Thus, 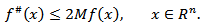 | (2.1) |
It is known that (see e.g. [18]) if 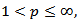 then
then 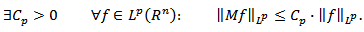 Hence, from (2.1) we get
Hence, from (2.1) we get 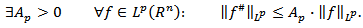 The last relation means that the operator
The last relation means that the operator 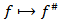 is the operator of the type
is the operator of the type 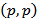 for
for 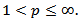 It is also known [18] that if
It is also known [18] that if 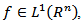 then there exists a number
then there exists a number 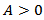 such that for any
such that for any 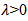
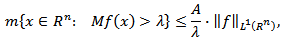 where
where 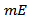 denotes the Lebesgue measure of the set
denotes the Lebesgue measure of the set 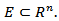 Hence, from (2.1) we get
Hence, from (2.1) we get 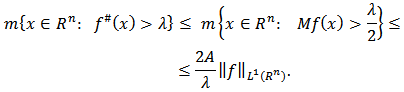 Thus, if
Thus, if 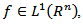 then there exist the number
then there exist the number 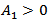 such that for any
such that for any 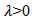
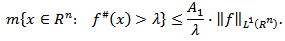 The last relation means that the operator
The last relation means that the operator 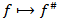 is the operator of weak type (1,1). In the case
is the operator of weak type (1,1). In the case 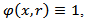 we denote the function
we denote the function 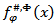 by
by 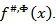 Then for the function
Then for the function 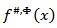 we have
we have 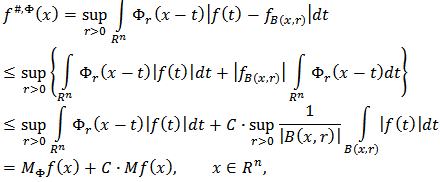 where
where 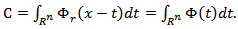 Thus,
Thus, 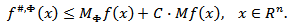 | (2.2) |
From the inequality (2.2), the Hardy-Littlewood maximal theorem and theorem 2 of chapter 3 [18] we get the following facts. If 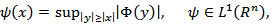 then for
then for 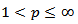
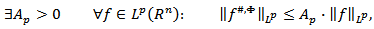 and for
and for 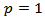 we have
we have 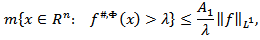
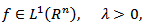 where the positive constant
where the positive constant 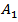 is independent on
is independent on 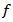 and
and 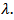 Thus, at the indicated conditions on the function
Thus, at the indicated conditions on the function 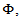 the operator
the operator 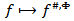 is the operator of type
is the operator of type 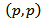 for
for 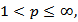 and is also weak type (1,1) operator.
and is also weak type (1,1) operator.
3. Relations between Maximal Function and Metric Characteristic. Some Inequalities
In this section we’ll assume that 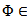
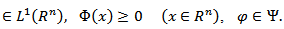 Proposition 3.1. If
Proposition 3.1. If 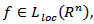 then the following equality is satisfied
then the following equality is satisfied 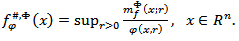 | (3.1) |
Proof: From the definition of the function 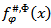 we get
we get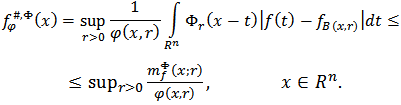 | (3.2) |
On the other hand, for any 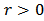 and
and 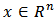 we have
we have 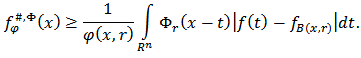 Hence it follows that
Hence it follows that 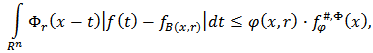 therefore
therefore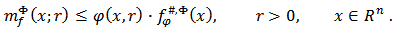 So,
So, 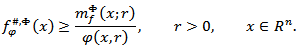 From the last inequality we get
From the last inequality we get 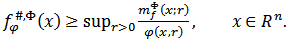 | (3.3) |
Equality (3.1) is obtained from inequalities (3.2) and (3.3). Lemma 3.1. Let 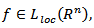 and
and 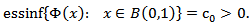 | (3.4) |
Then for any constant 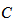 the following inequality is true
the following inequality is true 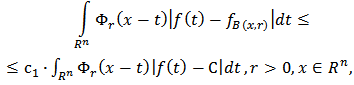 | (3.5) |
where the positive constant 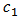 depends only on the
depends only on the 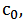 dimension
dimension 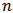 and on the quantity
and on the quantity 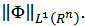 Proof. Let
Proof. Let 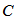 be any constant. Then we have
be any constant. Then we have 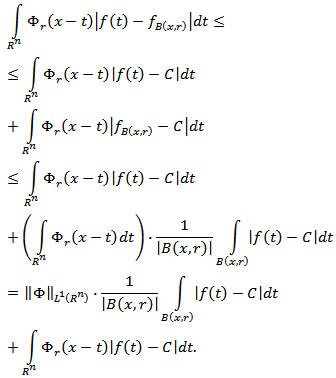 Thus, for all
Thus, for all 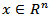 and
and 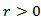
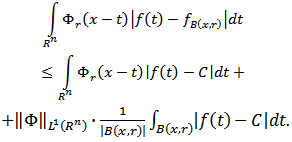 | (3.6) |
On the other hand, by means of condition (3.4) we get 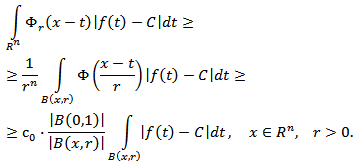 Hence
Hence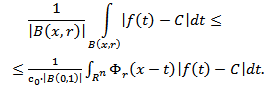 | (3.7) |
Using this inequality, from (3.6) we get 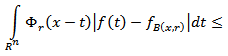
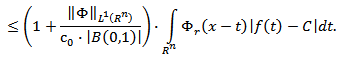 Proposition 3.2. Let
Proposition 3.2. Let 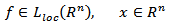 and condition (3.4) be satisfied. Then the following inequality is true
and condition (3.4) be satisfied. Then the following inequality is true 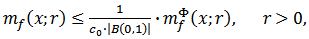 | (3.8) |
Proof. If we take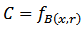 , then the validity of inequality (3.8) is obtained from relation (3.7). Remark 3.1. Note that for the function
, then the validity of inequality (3.8) is obtained from relation (3.7). Remark 3.1. Note that for the function 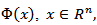 satisfying condition (3.4) we can take, for instance, the following functions: 1)
satisfying condition (3.4) we can take, for instance, the following functions: 1) 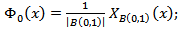 2)
2) 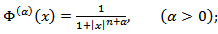 3)
3) 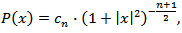 where
where 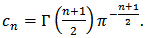 Verify, that if
Verify, that if 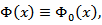 then
then 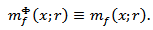 | (3.9) |
Indeed, if 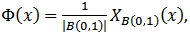 then
then 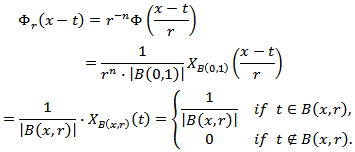 Therefore for this function
Therefore for this function 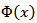 we have
we have 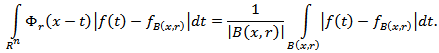 Hence, equality (3.9) is obtained. We note that the quantity
Hence, equality (3.9) is obtained. We note that the quantity 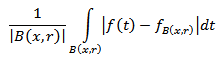 is said to be mean oscillation of the function
is said to be mean oscillation of the function 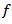 in the ball
in the ball 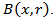 Remark 3.2. In the case of
Remark 3.2. In the case of 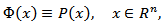 the quantity
the quantity 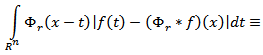
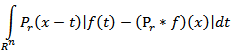 is called a harmonic oscillation of the function
is called a harmonic oscillation of the function 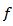 (see [1]). In the paper [2] it has been proven that
(see [1]). In the paper [2] it has been proven that 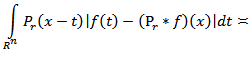
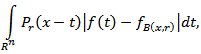 where the constants in the relation
where the constants in the relation 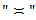 depend only on the dimension
depend only on the dimension 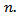 Hence it is obtained that
Hence it is obtained that 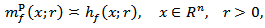 where
where 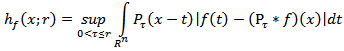 (see [2]). Let's show that the relation
(see [2]). Let's show that the relation 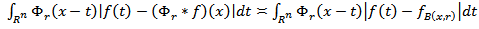 | (3.10) |
takes place for wider class of functions  Proposition 3.3. Let
Proposition 3.3. Let 
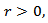
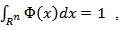 and condition (3.4) is satisfied. Then the relation (3.10) is true, where the constants in the relation
and condition (3.4) is satisfied. Then the relation (3.10) is true, where the constants in the relation 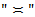 depend only on the constant
depend only on the constant 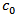 and dimension
and dimension 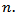 Proof. For convenience we will introduce the following notations:
Proof. For convenience we will introduce the following notations: 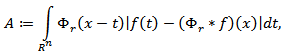
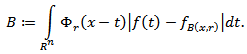 Then we get
Then we get 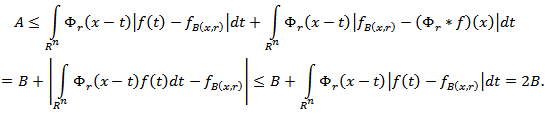 Thus
Thus 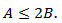 | (3.11) |
On the other hand, 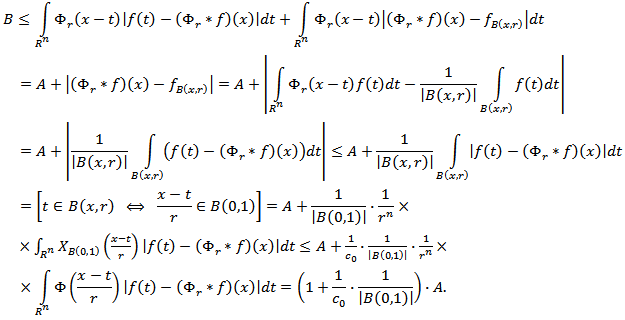 Thus
Thus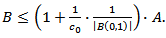 | (3.12) |
Inequalities (3.11) and (3.12) prove the required relation (3.10).
4. Estimations of -Maximal Functions by Maximal Functions
Proposition 4.1. If 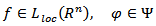 and the function
and the function 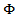 satisfies condition (3.4), then the following inequality is true
satisfies condition (3.4), then the following inequality is true 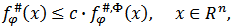 | (4.1) |
where 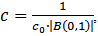 and
and 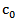 is а constant from inequality (3.4). Proof. By means of Proposition 3.1 and inequality (3.8) we get
is а constant from inequality (3.4). Proof. By means of Proposition 3.1 and inequality (3.8) we get 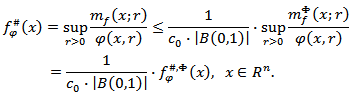 Proposition 4.2. [2]. Let
Proposition 4.2. [2]. Let 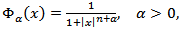
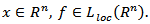 Then the following inequality is true
Then the following inequality is true 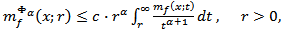 | (4.2) |
where the constant 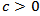 is independent on
is independent on 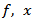 and
and 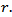 Lemma 4.1. If
Lemma 4.1. If 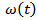 is a non-negative, monotone increasing function on the interval
is a non-negative, monotone increasing function on the interval 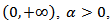 and
and 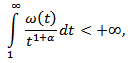 then the function
then the function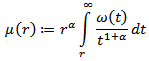 also monotone increases on interval
also monotone increases on interval 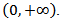 Proof. Let
Proof. Let 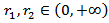 and
and 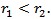 Then we have
Then we have 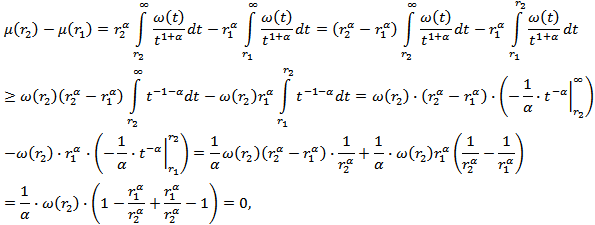 i.e.
i.e. 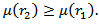 Proposition 4.3. Let
Proposition 4.3. Let 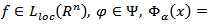
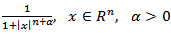 and
and 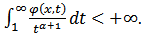 | (4.3) |
Then the following inequality holds 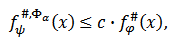 | (4.4) |
where 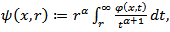 and the positive constant
and the positive constant 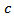 does not depend on
does not depend on 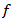 and
and 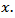 Proof. By means of relations (3.1), (4.2) and (4.3), we have
Proof. By means of relations (3.1), (4.2) and (4.3), we have 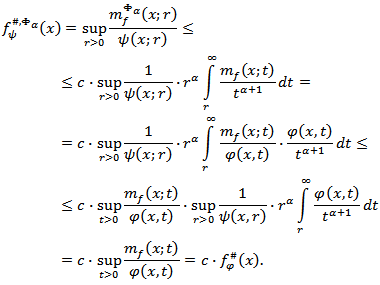 Corollary 4.1. Let
Corollary 4.1. Let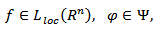
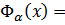
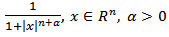 and
and 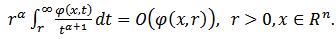 | (4.5) |
Then the following inequality holds 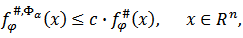 | (4.6) |
where the positive constant 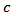 is independent on
is independent on 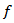 and
and 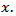 Proof. If condition (4.5) is satisfied, then by virtue of proposition 4.3 the inequality (4.4) holds. Furthermore, from a condition (4.5) follows that
Proof. If condition (4.5) is satisfied, then by virtue of proposition 4.3 the inequality (4.4) holds. Furthermore, from a condition (4.5) follows that 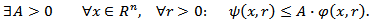 Taking this into account, we have
Taking this into account, we have 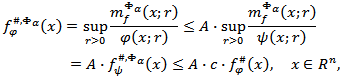 where
where 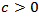 is a constant from inequality (4.4). Proposition 4.4. Let
is a constant from inequality (4.4). Proposition 4.4. Let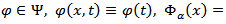
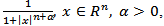 and
and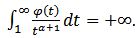 | (4.7) |
Then there exists a function 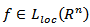 such that
such that 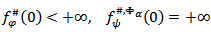 for any function
for any function 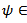
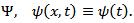 Proof. Consider the function
Proof. Consider the function 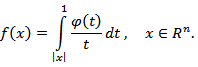 In the paper [14] it is shown that
In the paper [14] it is shown that 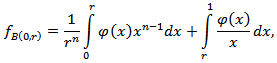
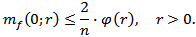 From the last inequality it follows that
From the last inequality it follows that 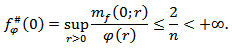 Further, for
Further, for 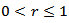 we have
we have 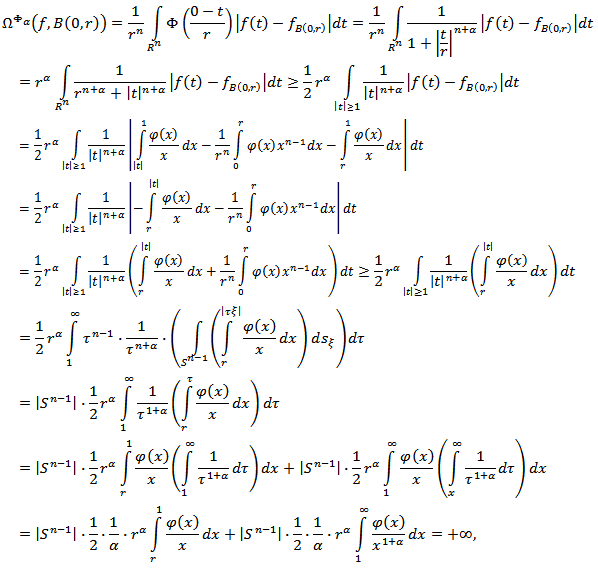 where
where 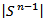 denotes the area of the surface of a unit sphere
denotes the area of the surface of a unit sphere 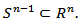 Thus, for
Thus, for 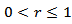 the equality
the equality 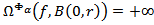 is true. Therefore, for any function
is true. Therefore, for any function 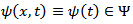
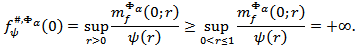 Corollary 4.2. Let
Corollary 4.2. Let 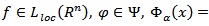
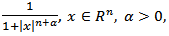 and condition (4.5) satisfied. Then there exist the numbers
and condition (4.5) satisfied. Then there exist the numbers 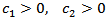 such that
such that 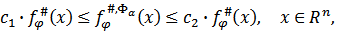 where the constants
where the constants 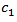 and
and 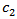 are independent on
are independent on 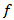 and
and 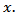 Now consider the case of the function
Now consider the case of the function 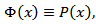 where
where 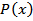 is a Poisson kernel. It is easy to see that there exist the numbers
is a Poisson kernel. It is easy to see that there exist the numbers 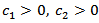 such that for all
such that for all 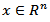 the relation.
the relation.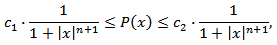 holds. That is
holds. That is 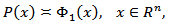 where
where 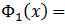
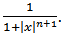 Hence it follows that if
Hence it follows that if 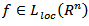 and
and 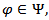 then the following relations are true
then the following relations are true 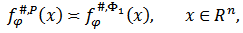
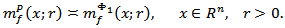 By means of these considerations, from corollary 4.2 we get Corollary 4.3. Let
By means of these considerations, from corollary 4.2 we get Corollary 4.3. Let 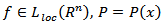 be a Poisson kernel,
be a Poisson kernel, 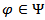 and
and 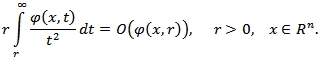 Then the following relation is true
Then the following relation is true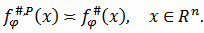
5. Conclusions
Maximal functions play an important role in the study of differentiation of functions, almost everywhere convergence of singular integrals, mapping properties of singular integral operators and potential type integral operators. Maximal functions measuring smoothness are useful in the study of smoothness of functions and the mapping properties of various operators of Harmonic Analysis on smoothness spaces. The main theme of this paper is to study certain maximal functions and Φ-maximal functions measuring smoothness. Relations between maximal and Φ-maximal functions measuring smoothness are studied. These relations allow to unite and compare the results received in terms of various characteristics.
References
| [1] | Blasco O., Perez M.A. On functions of integrable mean oscillation. Rev. Mat. Complut., 2005, v.18, No2, pp.465-477. |
| [2] | Rzaev R.M., Aliyeva L.R. Mean oscillation, Φ-oscillation and harmonic oscillation. Trans. NAS Azerb., 2010, v.30, No1, pp.167-176. |
| [3] | Peetre J. On the theory of spaces. J. Functional Analysis, 1969, v.4, p.71-87. |
| [4] | Gadzhiev N.M., Rzaev R.M. On the order of locally summable functions approximation by singular integrals. Funct. Approx. Comment. Math., 1992, v.20, pp.35-40. |
| [5] | Fefferman Ch., Stein E.M. spaces of several variables. Acta Math., 1972, v.129, №3-4, pp. 137-193. |
| [6] | Calderon A.P. Estimates for singular integral operators in terms of maximal functions. Studia Math., 1972, v.44, p. 167-186. |
| [7] | Calderon A.P., Scott R. Sobolev type inequalities for . Studia Math., 1978, v.62, p.75-92. |
| [8] | DeVore R., Sharpley R. Maximal functions measuring smoothness. Mem. Amer. Math. Soc., 1984, v.47, №293, p. 1-115. |
| [9] | Kolyada V.I. Estimates of maximal functions measuring local smoothness. Analysis Mathematica, 1999, v.25, p.277-300. |
| [10] | Nakai E., Sumitomo H. On generalized Riesz potentials and spaces of some smooth functions. Scien. Math. Japan. 2001, v.54, p.463-472. |
| [11] | Rzaev R.M. On some maximal functions, measuring smoothness, and metric characteristics. Trans. NAS Azerb., 1999, v.19, №5, pp.118-124. |
| [12] | Rzaev R.M. Properties of singular integrals in terms of maximal functions measuring smoothness. Eurasian Math. J., 2013, v.4, No3, pp.107-119. |
| [13] | Rzaev R.M., Aliyev F.N. Some embedding theorems and properties of Riesz poitentials. American Journal of Mathematics and Statistics., 2013, v.3, No6, pp.445-453. |
| [14] | Rzaev R.M. On approximation of locally summable functions by singular integrals in terms of mean oscillation and some applications. Preprint Inst. Phys. Natl. Acad. Sci. Azerb., 1992, №1, p.1-43 (Russian). |
| [15] | Rzaev R.M. A multidimensional singular integral operator in the spaces defined by conditions on the k-th order mean oscillation. Dokady Mathematics, 1997, v.56, No2, pp.747-749. |
| [16] | Rzaev R.M., Aliyeva L.R. On local properties of functions and singular integrals in terms of the mean oscillation. Cent. Eur. J. Math., 2008, v.6, No4, p.595-609. |
| [17] | Stein E.M. Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton University Press. Princeton, New J., 1993. |
| [18] | Stein E.M. Singular integrals and differentiability properties of functions. Princeton University Press. Princeton, New J., 1970. |
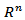 be
be 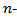 dimensional Euclidean space,
dimensional Euclidean space, 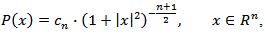
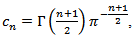
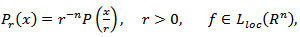
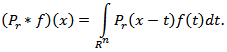 Note that the quantity
Note that the quantity 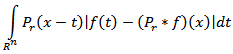 is called harmonic oscillation (see, for instance, [1], [2]). In work [2] it has proven that
is called harmonic oscillation (see, for instance, [1], [2]). In work [2] it has proven that 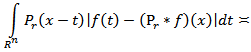
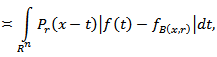 where
where 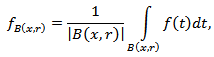
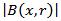 denotes the volume of ball
denotes the volume of ball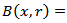
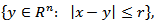 and constants in the relation
and constants in the relation 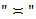 depend only on dimension
depend only on dimension 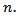 (For positive functions
(For positive functions 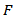 and
and 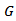 we will use the notation
we will use the notation 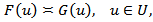 if there exist positive constants
if there exist positive constants 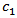 and
and 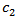 such that
such that 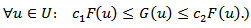 Let
Let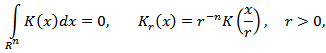
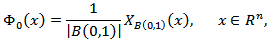 where
where 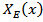 is a characteristic function of the set
is a characteristic function of the set 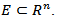 It is easy to see that
It is easy to see that 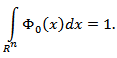 In the papers of some other authors (see e.g. [3], [4]) the quantity
In the papers of some other authors (see e.g. [3], [4]) the quantity 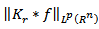 is chosen as a characteristic to determine homogeneous classes of Besov. We can write the quantity
is chosen as a characteristic to determine homogeneous classes of Besov. We can write the quantity 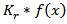 in the following form
in the following form 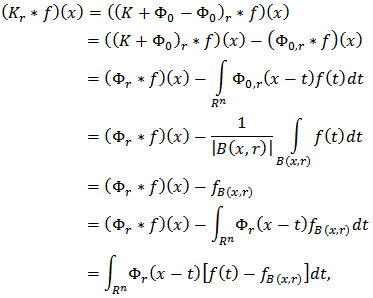 where
where 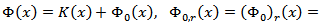
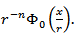 It is obvious that
It is obvious that 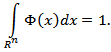 Thus,
Thus, 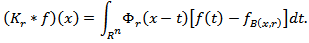 Hence we have
Hence we have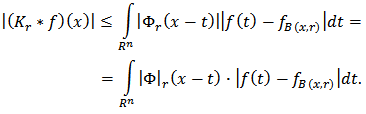 In the present paper, for the principal characteristic we take the quantity
In the present paper, for the principal characteristic we take the quantity 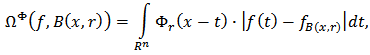 where
where 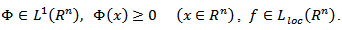
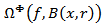 is said to be
is said to be 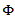 -oscillation of the function
-oscillation of the function 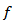 in the ball
in the ball 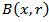 [2]. It is known that maximal functions measuring smoothness play an important role in the study of properties of integral operators and other objects of Harmonic Analysis. The main topic of this paper is the study of certain generalized maximal function (
[2]. It is known that maximal functions measuring smoothness play an important role in the study of properties of integral operators and other objects of Harmonic Analysis. The main topic of this paper is the study of certain generalized maximal function (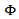 -maximal function) measuring smoothness. The paper is organized as follows. Section 2 has auxiliary character and presents the basic definitions, some notation and well-known facts. In section 3 the relations between maximal function and metric characteristic are investigated and some useful inequalities were obtained. In section 4 estimations between
-maximal function) measuring smoothness. The paper is organized as follows. Section 2 has auxiliary character and presents the basic definitions, some notation and well-known facts. In section 3 the relations between maximal function and metric characteristic are investigated and some useful inequalities were obtained. In section 4 estimations between 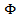 -maximal function and maximal function was obtained. The main results are given in Propositions 3.1, 3.3, 4.1, 4.3 and 4.4.
-maximal function and maximal function was obtained. The main results are given in Propositions 3.1, 3.3, 4.1, 4.3 and 4.4. 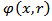 be defined on the set
be defined on the set 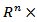
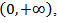 takes only positive values, and monotone increases with respect to the argument
takes only positive values, and monotone increases with respect to the argument 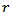 on the interval
on the interval 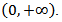 We denote the class of all functions
We denote the class of all functions 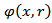 with the above mentioned properties by
with the above mentioned properties by 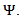 Let
Let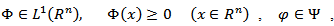
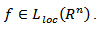 Let’s introduce the following Φ-maximal function
Let’s introduce the following Φ-maximal function 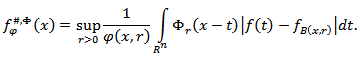 We also introduce the following metric Φ-characteristic
We also introduce the following metric Φ-characteristic 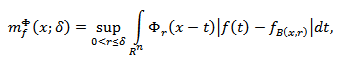
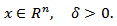 Consider the known special cases of the introduced maximal function
Consider the known special cases of the introduced maximal function 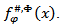 1) If
1) If 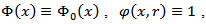 then
then 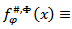
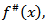 where
where 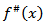 is the maximal function which is introduced in the paper [5]. 2) If
is the maximal function which is introduced in the paper [5]. 2) If 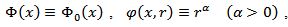 then
then 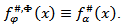 The maximal function
The maximal function 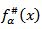 was mentioned in the papers [6], [7]. In paper [8] the function
was mentioned in the papers [6], [7]. In paper [8] the function 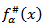 was investigated. 3) If
was investigated. 3) If 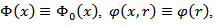 then the maximal function
then the maximal function 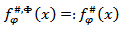 may be found in the papers [9], [10], [11], [12], [13] and others. Now let’s consider special cases of metric Φ-characteristic
may be found in the papers [9], [10], [11], [12], [13] and others. Now let’s consider special cases of metric Φ-characteristic 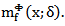 1) If
1) If 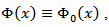 then
then 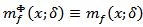 (see section 3), where
(see section 3), where 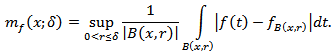 Note that the function
Note that the function 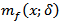 was first introduced in the paper [14] (see also, [15], [16]). 2) Let
was first introduced in the paper [14] (see also, [15], [16]). 2) Let 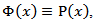 where
where 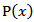 is the Poisson kernel, i.e.
is the Poisson kernel, i.e. 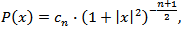 where
where 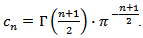 Global variant of the characteristic
Global variant of the characteristic 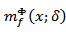 (more precisely, the equivalent characteristic to it which is called a modulus of harmonic oscillation) for periodic functions of one variable may be found in the paper [1]. It is known that Hardy-Littlewood’s maximal function is determined by the equality
(more precisely, the equivalent characteristic to it which is called a modulus of harmonic oscillation) for periodic functions of one variable may be found in the paper [1]. It is known that Hardy-Littlewood’s maximal function is determined by the equality 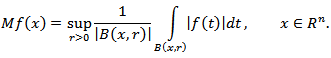 For case of
For case of 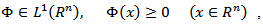
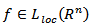 the following maximal function is also considered [17]
the following maximal function is also considered [17]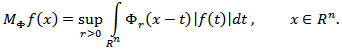 It is easy to see that if
It is easy to see that if 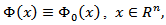 then
then 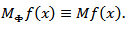 From the definition of a maximal function
From the definition of a maximal function 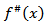 it follows that
it follows that 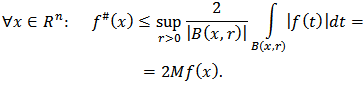 Thus,
Thus, 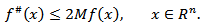
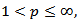 then
then 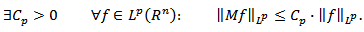 Hence, from (2.1) we get
Hence, from (2.1) we get 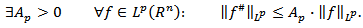 The last relation means that the operator
The last relation means that the operator 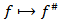 is the operator of the type
is the operator of the type 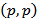 for
for 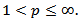 It is also known [18] that if
It is also known [18] that if 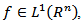 then there exists a number
then there exists a number 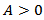 such that for any
such that for any 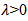
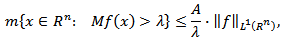 where
where 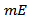 denotes the Lebesgue measure of the set
denotes the Lebesgue measure of the set 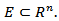 Hence, from (2.1) we get
Hence, from (2.1) we get 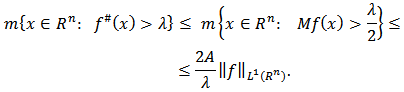 Thus, if
Thus, if 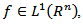 then there exist the number
then there exist the number 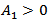 such that for any
such that for any 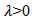
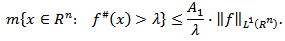 The last relation means that the operator
The last relation means that the operator 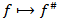 is the operator of weak type (1,1). In the case
is the operator of weak type (1,1). In the case 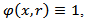 we denote the function
we denote the function 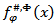 by
by 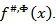 Then for the function
Then for the function 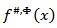 we have
we have 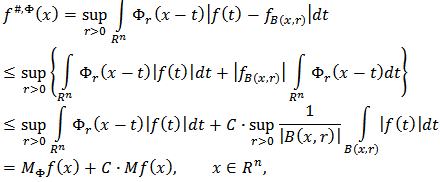 where
where 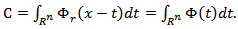 Thus,
Thus, 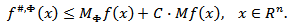
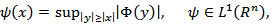 then for
then for 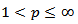
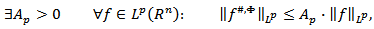 and for
and for 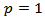 we have
we have 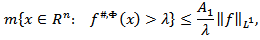
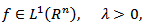 where the positive constant
where the positive constant 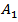 is independent on
is independent on 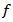 and
and 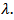 Thus, at the indicated conditions on the function
Thus, at the indicated conditions on the function 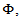 the operator
the operator 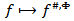 is the operator of type
is the operator of type 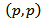 for
for 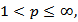 and is also weak type (1,1) operator.
and is also weak type (1,1) operator. 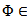
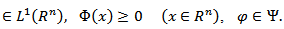 Proposition 3.1. If
Proposition 3.1. If 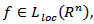 then the following equality is satisfied
then the following equality is satisfied 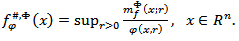
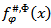 we get
we get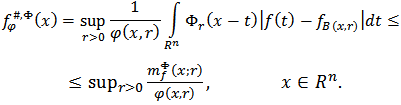
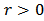 and
and 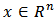 we have
we have 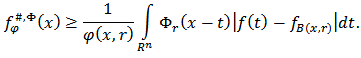 Hence it follows that
Hence it follows that 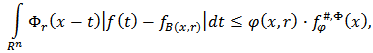 therefore
therefore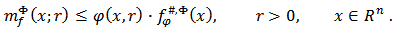 So,
So, 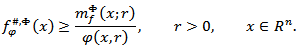 From the last inequality we get
From the last inequality we get 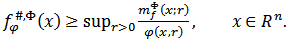
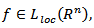 and
and 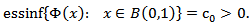
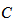 the following inequality is true
the following inequality is true 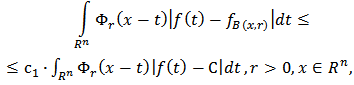
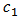 depends only on the
depends only on the 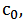 dimension
dimension 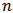 and on the quantity
and on the quantity 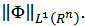 Proof. Let
Proof. Let 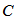 be any constant. Then we have
be any constant. Then we have 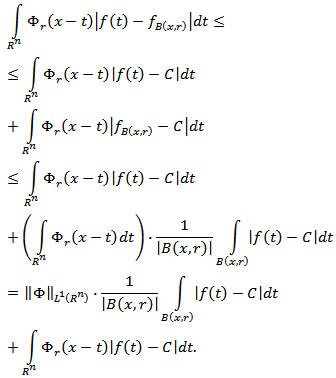 Thus, for all
Thus, for all 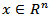 and
and 
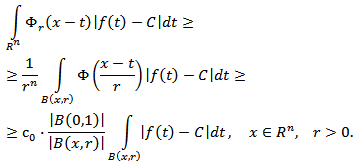 Hence
Hence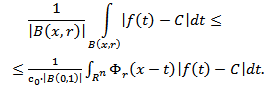
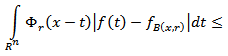
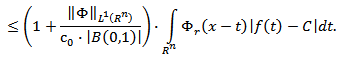 Proposition 3.2. Let
Proposition 3.2. Let 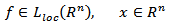 and condition (3.4) be satisfied. Then the following inequality is true
and condition (3.4) be satisfied. Then the following inequality is true 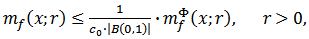
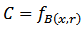 , then the validity of inequality (3.8) is obtained from relation (3.7). Remark 3.1. Note that for the function
, then the validity of inequality (3.8) is obtained from relation (3.7). Remark 3.1. Note that for the function 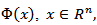 satisfying condition (3.4) we can take, for instance, the following functions: 1)
satisfying condition (3.4) we can take, for instance, the following functions: 1) 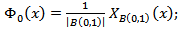 2)
2) 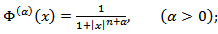 3)
3) 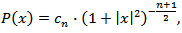 where
where 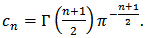 Verify, that if
Verify, that if 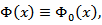 then
then 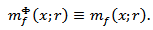
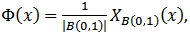 then
then 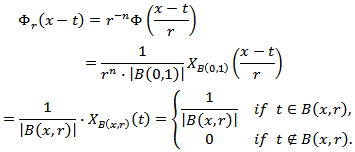 Therefore for this function
Therefore for this function 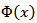 we have
we have 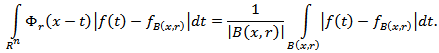 Hence, equality (3.9) is obtained. We note that the quantity
Hence, equality (3.9) is obtained. We note that the quantity 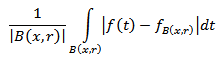 is said to be mean oscillation of the function
is said to be mean oscillation of the function 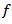 in the ball
in the ball 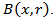 Remark 3.2. In the case of
Remark 3.2. In the case of 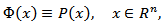 the quantity
the quantity 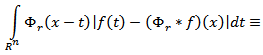
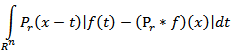 is called a harmonic oscillation of the function
is called a harmonic oscillation of the function 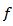 (see [1]). In the paper [2] it has been proven that
(see [1]). In the paper [2] it has been proven that 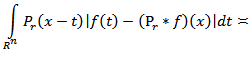
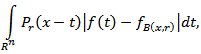 where the constants in the relation
where the constants in the relation 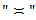 depend only on the dimension
depend only on the dimension 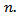 Hence it is obtained that
Hence it is obtained that 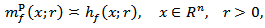 where
where 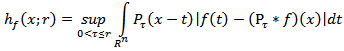 (see [2]). Let's show that the relation
(see [2]). Let's show that the relation 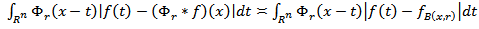
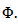 Proposition 3.3. Let
Proposition 3.3. Let 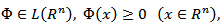
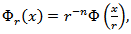
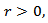
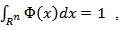 and condition (3.4) is satisfied. Then the relation (3.10) is true, where the constants in the relation
and condition (3.4) is satisfied. Then the relation (3.10) is true, where the constants in the relation 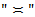 depend only on the constant
depend only on the constant 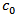 and dimension
and dimension 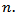 Proof. For convenience we will introduce the following notations:
Proof. For convenience we will introduce the following notations: 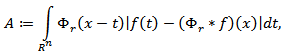
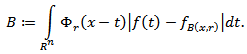 Then we get
Then we get 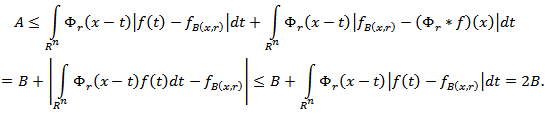 Thus
Thus 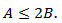
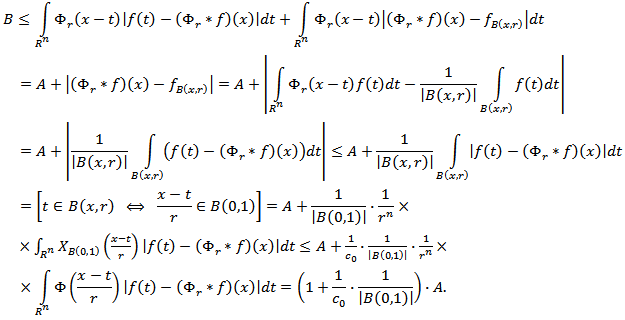 Thus
Thus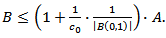
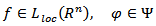 and the function
and the function 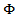 satisfies condition (3.4), then the following inequality is true
satisfies condition (3.4), then the following inequality is true 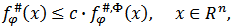
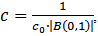 and
and 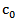 is а constant from inequality (3.4). Proof. By means of Proposition 3.1 and inequality (3.8) we get
is а constant from inequality (3.4). Proof. By means of Proposition 3.1 and inequality (3.8) we get 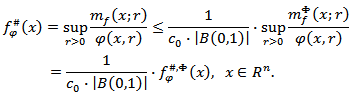 Proposition 4.2. [2]. Let
Proposition 4.2. [2]. Let 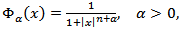
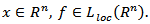 Then the following inequality is true
Then the following inequality is true 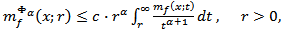
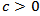 is independent on
is independent on 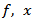 and
and 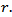 Lemma 4.1. If
Lemma 4.1. If 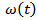 is a non-negative, monotone increasing function on the interval
is a non-negative, monotone increasing function on the interval 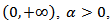 and
and 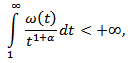 then the function
then the function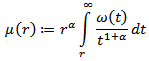 also monotone increases on interval
also monotone increases on interval 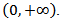 Proof. Let
Proof. Let 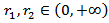 and
and  Then we have
Then we have  i.e.
i.e.  Proposition 4.3. Let
Proposition 4.3. Let 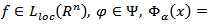
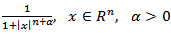 and
and 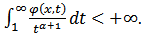
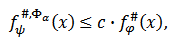
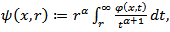 and the positive constant
and the positive constant 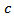 does not depend on
does not depend on 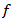 and
and 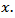 Proof. By means of relations (3.1), (4.2) and (4.3), we have
Proof. By means of relations (3.1), (4.2) and (4.3), we have 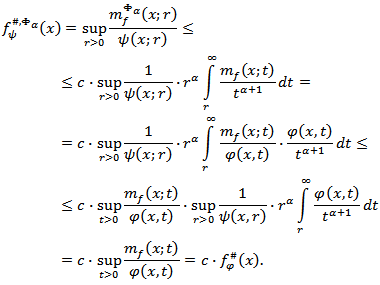 Corollary 4.1. Let
Corollary 4.1. Let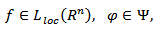
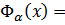
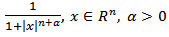 and
and 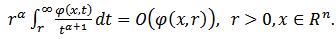
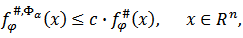
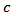 is independent on
is independent on 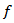 and
and 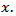 Proof. If condition (4.5) is satisfied, then by virtue of proposition 4.3 the inequality (4.4) holds. Furthermore, from a condition (4.5) follows that
Proof. If condition (4.5) is satisfied, then by virtue of proposition 4.3 the inequality (4.4) holds. Furthermore, from a condition (4.5) follows that 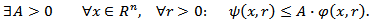 Taking this into account, we have
Taking this into account, we have 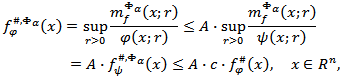 where
where 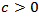 is a constant from inequality (4.4). Proposition 4.4. Let
is a constant from inequality (4.4). Proposition 4.4. Let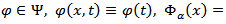
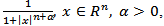 and
and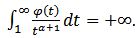
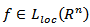 such that
such that 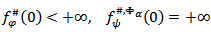 for any function
for any function 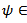
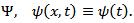 Proof. Consider the function
Proof. Consider the function 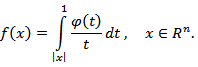 In the paper [14] it is shown that
In the paper [14] it is shown that 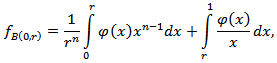
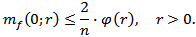 From the last inequality it follows that
From the last inequality it follows that 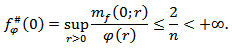 Further, for
Further, for 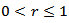 we have
we have 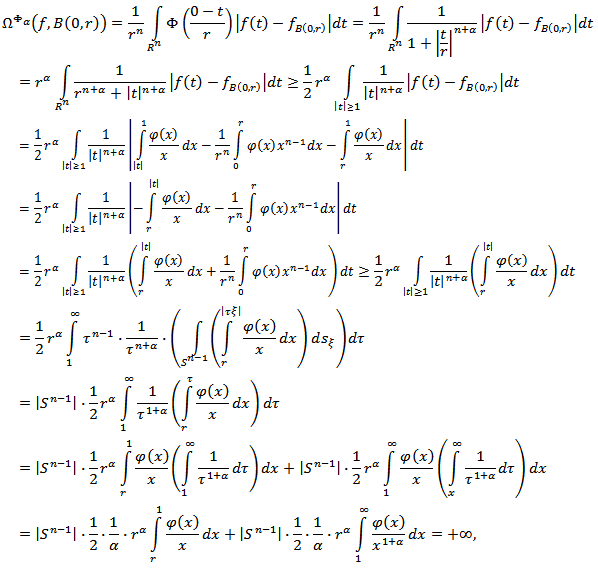 where
where 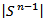 denotes the area of the surface of a unit sphere
denotes the area of the surface of a unit sphere 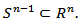 Thus, for
Thus, for 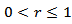 the equality
the equality 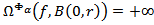 is true. Therefore, for any function
is true. Therefore, for any function 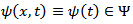
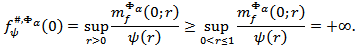 Corollary 4.2. Let
Corollary 4.2. Let 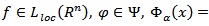
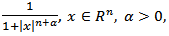 and condition (4.5) satisfied. Then there exist the numbers
and condition (4.5) satisfied. Then there exist the numbers 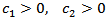 such that
such that 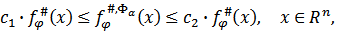 where the constants
where the constants 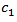 and
and 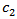 are independent on
are independent on 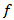 and
and 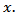 Now consider the case of the function
Now consider the case of the function 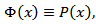 where
where 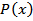 is a Poisson kernel. It is easy to see that there exist the numbers
is a Poisson kernel. It is easy to see that there exist the numbers 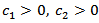 such that for all
such that for all 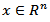 the relation.
the relation.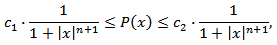 holds. That is
holds. That is 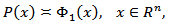 where
where 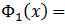
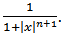 Hence it follows that if
Hence it follows that if 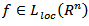 and
and 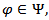 then the following relations are true
then the following relations are true 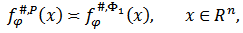
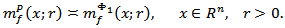 By means of these considerations, from corollary 4.2 we get Corollary 4.3. Let
By means of these considerations, from corollary 4.2 we get Corollary 4.3. Let 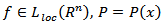 be a Poisson kernel,
be a Poisson kernel, 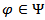 and
and 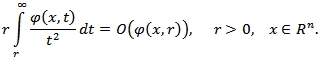 Then the following relation is true
Then the following relation is true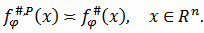
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML