-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2015; 5(2): 43-51
doi:10.5923/j.ajms.20150502.01
Analyzing System Reliability Using Fuzzy Mixture Generalized Linear Failure Rate Distribution
M. A. El-Damcese1, Dina. A. Ramadan2
1Mathematics Department, Faculty of Science, Tanta University, Tanta, Egypt
2Mathematics Department, Faculty of Science, Mansoura University, Mansoura, Egypt
Correspondence to: M. A. El-Damcese, Mathematics Department, Faculty of Science, Tanta University, Tanta, Egypt.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
In this paper, some statistics properties of the mixture generalized linear failure rate distribution (or MGLFRD) and MGLFRD with fuzzy parameters methods have been investigated. Formulas of a fuzzy reliability function, fuzzy hazard function and their α-cut set are presented.
Keywords: MGLFRD, Fuzzy reliability function, Fuzzy hazard function
Cite this paper: M. A. El-Damcese, Dina. A. Ramadan, Analyzing System Reliability Using Fuzzy Mixture Generalized Linear Failure Rate Distribution, American Journal of Mathematics and Statistics, Vol. 5 No. 2, 2015, pp. 43-51. doi: 10.5923/j.ajms.20150502.01.
Article Outline
1. Introduction
- The mixture distributions have provided a mathematical-based approach to the statistical modeling of a wide variety of random phenomena. The mixture distributions are useful and flexible models to analyze random durations in a possibly heterogeneous population. In many applications, available data can be considered as the data coming from a mixture population of two or more distributions. Therefore mixture distributions play a vital role in many practical applications. For example, direct applications of finite mixture models are in fisheries research, economics, medicine, psychology, paleoanthropology, botany, agriculture, zoology, life testing and reliability, among others. Indirect applications include outliers, Gaussian sums, cluster analysis, latent structure models, modeling prior densities, empirical Bayes method and nonparametric density estimation.There are several methods and models in classical reliability theory, which assume that all parameters of lifetime density functions are precise. However, in the real world applications, randomness and fuzziness are often mixed up in the lifetimes of systems. However, the parameters sometimes cannot record precisely due to machine errors, experiment, personal judgment, estimation or some other unexpected situations. When parameter in the lifetime distribution is fuzzy, the conventional reliability system may have difficulty for handling reliability and hazard functions. The theory of fuzzy reliability was proposed and development by several authors (Cai et al. [1], [2]; Cai, [3]; Chen and Mon [4]; Hammer [5]; Onisawa and Kacprzyk [6]; Utkin and Gurov, [7]). Aliev and Kara [8] considered fuzzy system reliability analysis using time dependent fuzzy set and the concept of alpha-cut. Utkin [9], [10] discussed imprecise reliability models for the general lifetime distribution classes. He applied the theory of imprecise probability to reliability analysis. Wu [11] considered fuzzy Bayesian system reliability assessment based on exponential distribution. Guo et al. [12] proposed a credibility hazard concept associated with fuzzy lifetimes. Guo et al. [13] considered random fuzzy variable modeling on repairable system. Yao et al. [14] applied a statistical methodology in fuzzy system reliability analysis and provided a fuzzy estimation of reliability. Karpisek et al. [15] described two fuzzy reliability models based on the Weibull fuzzy distribution. Baloui Jamkhaneh and Nozari [16] investigated fuzzy system reliability analysis based on confidence interval. Garg et al. [17] considered reliability analysis of the engineering systems using intuitionist fuzzy set theory. Pak et al. [18] presented a Bayesian approach to estimate the parameter and reliability function of Rayleigh distribution from fuzzy lifetime data. Baloui Jamkhaneh [19], [20] evaluated reliability function using fuzzy lifetime distribution.In this paper, mixture GLED have been used extensively in reliability and hazard analysis, we characterize the mixture of two GLED components. Some statistics properties are discussed. In addition, we study the two components mixture GLFRD with fuzzy parameters.
2. Two Component Mixture GLFRD
- Generalized linear failure rate distribution with three parameters (a, b, α) and denoted by GLFRD (a, b, α). The probability density function (pdf) of GLFRD (a, b, α) is given by
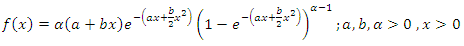 | (1) |
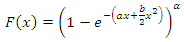 | (2) |
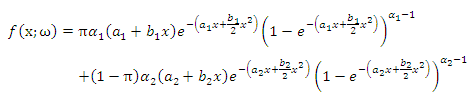 | (3) |
 are mixture weight, shape and scale parameters of subpopulation I respectively and
are mixture weight, shape and scale parameters of subpopulation I respectively and  is called the parameter vector of two components mixture GLFRD. Plots of density of two components mixture GLFRD for different parameter values are given in Figure 1.
is called the parameter vector of two components mixture GLFRD. Plots of density of two components mixture GLFRD for different parameter values are given in Figure 1.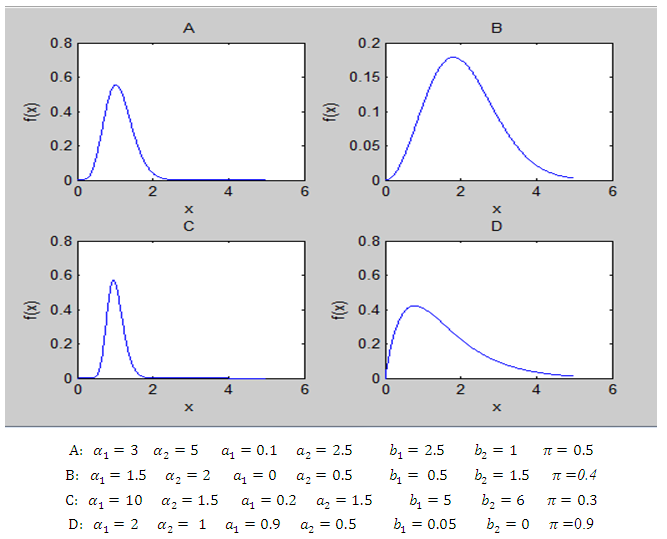 | Figure 1. Plots of density of two components mixture GLFRD for different parameter values |
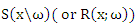 of two components mixture GLFRD is given as follows:
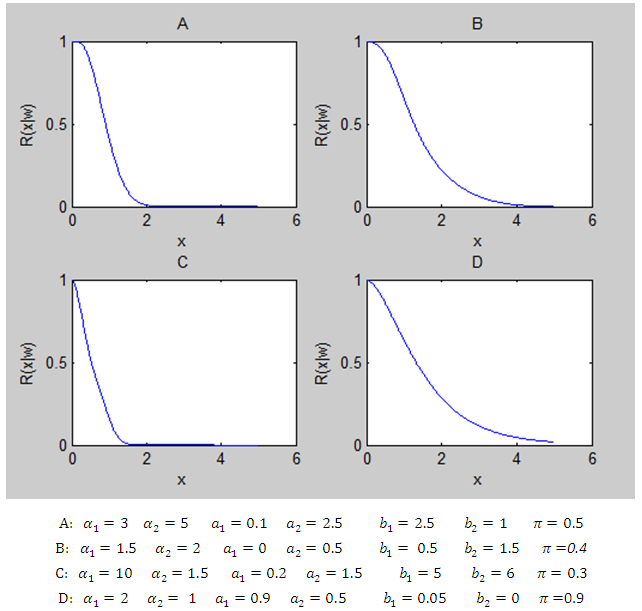
of two components mixture GLFRD is given as follows: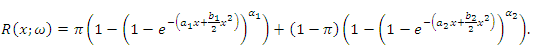 | (4) |
 | Figure 2. Plots of reliability functions of two components mixture GLFRD for different parameter values |
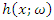 of two components mixture GLFRD is given as follows:
of two components mixture GLFRD is given as follows: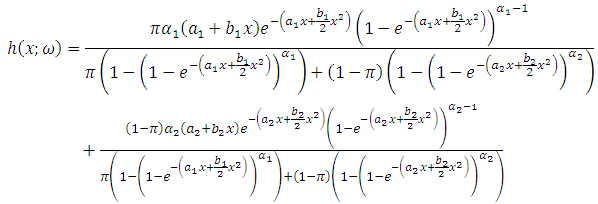 | (5) |
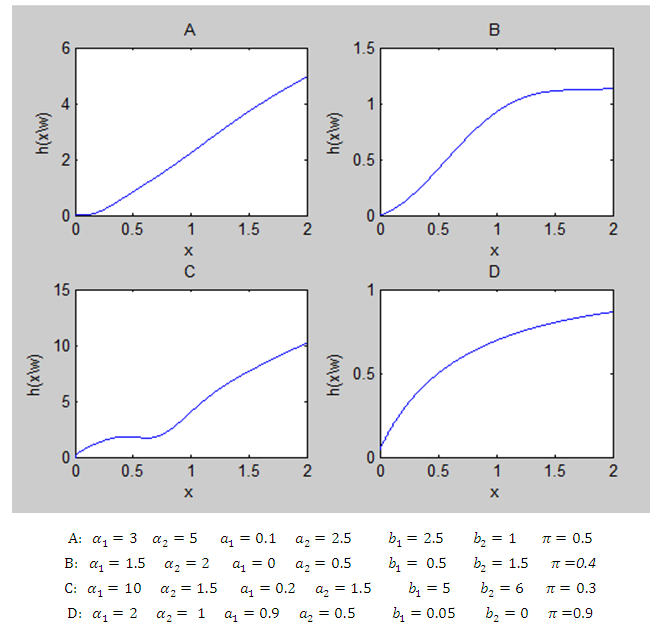 | Figure 3. Plots of hazard functions of two components mixture GLFRD for different parameter values |
3. Moments
- The following lemma gives the kth moment of two components mixture GLFRD (a, b, α), when
 .Lemma 3.1 If X has GLFRD
.Lemma 3.1 If X has GLFRD  , then the rth moment of X, say
, then the rth moment of X, say  , is given as followsFor
, is given as followsFor 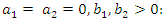
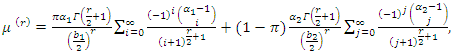 | (6) |
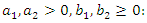
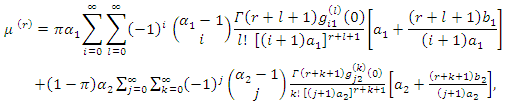 | (7) |
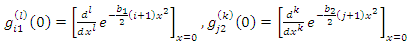 and
and 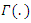 is the complete gamma function.Proof:
is the complete gamma function.Proof: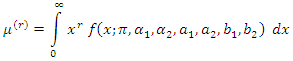 then substituting from (1) into the above relation we have
then substituting from (1) into the above relation we have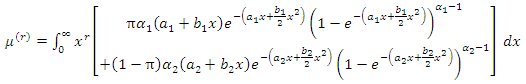 | (8) |
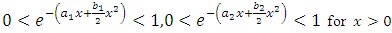 by using the binomial series expansion we have
by using the binomial series expansion we have 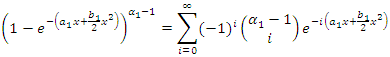 and
and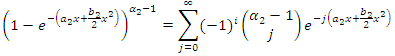 then,
then, 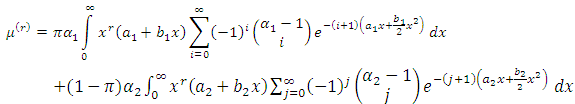 | (9) |
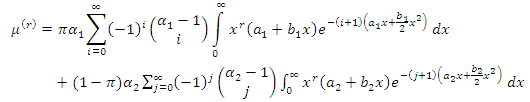 | (10) |
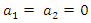 and
and 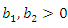 . In this case, the integral in (10) becomes
. In this case, the integral in (10) becomes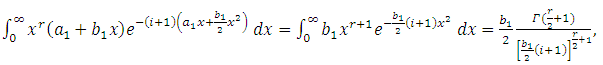 | (11) |
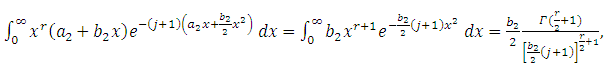 | (12) |
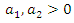 and
and 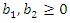 . For this case, using the Taylor expansion of the function
. For this case, using the Taylor expansion of the function 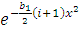 and
and 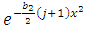 given by
given by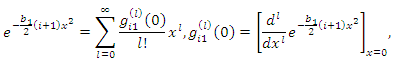 and
and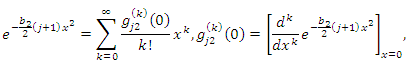 One can rewrite (10) as
One can rewrite (10) as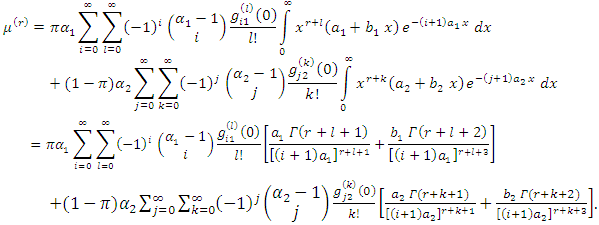 | (13) |
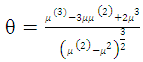 | (14) |
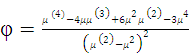 | (15) |
4. Fuzzy Reliability Function
- Sometimes we are faced with situations that the parameters of lifetime variable cannot be expressed as crisp values. They can be stated as “approximately”, “around”, “between”, or “about”. Fuzzy sets theory is a useful tool for conveying these expressions into mathematical functions. In this case, reliability theory should be considered with respect to fuzzy rules. Buckley [21] analyzed probability density functions when their parameters are fuzzy. We may consider the two components mixture GLFRD with fuzzy parameters and trapezoidal fuzzy number of
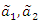 that is replaced instead of
that is replaced instead of 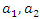 in consider the two components mixture GLFRD. In this case, we show the fuzzy probability of obtaining a value in the interval
in consider the two components mixture GLFRD. In this case, we show the fuzzy probability of obtaining a value in the interval 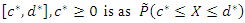 and compute its
and compute its 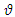 - cut as follows: (For more details, refer to Buckley [21])
- cut as follows: (For more details, refer to Buckley [21])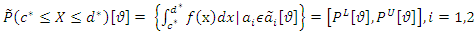 | (16) |
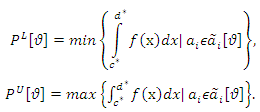 | (17) |
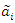 with a trapezoidal fuzzy number as
with a trapezoidal fuzzy number as 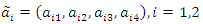 such that we can describe a membership function
such that we can describe a membership function  in the following manner:
in the following manner: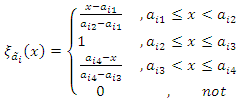 | (18) |
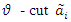 denote as
denote as 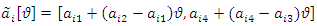 Fuzzy reliability (or fuzzy survival) function of two components mixture GLFRD distribution
Fuzzy reliability (or fuzzy survival) function of two components mixture GLFRD distribution 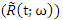 is the fuzzy probability a unit survives beyond time t. Let the random variable X denote lifetime of a system component, also let X follow fuzzy density function of two components mixture
is the fuzzy probability a unit survives beyond time t. Let the random variable X denote lifetime of a system component, also let X follow fuzzy density function of two components mixture 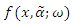 and fuzzy cumulative distribution function of two components mixture
and fuzzy cumulative distribution function of two components mixture 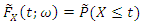 where parameter
where parameter 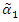 and
and 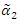 are a fuzzy number, in these conditions the fuzzy reliability function at time t of two components mixture GLFRD is defined as (See Baloui Jamkhaneh [20]):
are a fuzzy number, in these conditions the fuzzy reliability function at time t of two components mixture GLFRD is defined as (See Baloui Jamkhaneh [20]):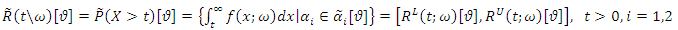 | (19) |
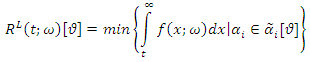 and
and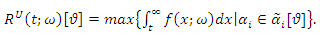 | (20) |
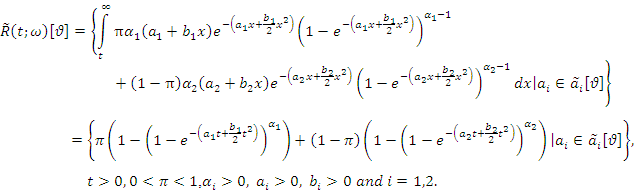 | (21) |
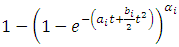 that is decreasing in terms of
that is decreasing in terms of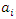 , we have:
, we have: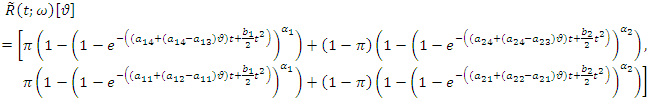 | (22) |
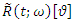 are two dimensional functions in terms of
are two dimensional functions in terms of 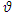 and
and 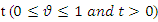 . For any particular value of
. For any particular value of 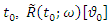 is a fuzzy number. Finally,
is a fuzzy number. Finally, 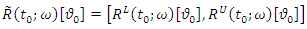 is
is 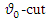 of fuzzy reliability of a unit. In this method, for any particular level of
of fuzzy reliability of a unit. In this method, for any particular level of 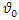 , upper and lower bound of
, upper and lower bound of 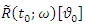 are two functions in terms of
are two functions in terms of 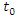 . So, in this case reliability curve is like a band with upper and lower bound whose width depends on the ambiguity parameter (See Baloui Jamkhaneh [19]). If
. So, in this case reliability curve is like a band with upper and lower bound whose width depends on the ambiguity parameter (See Baloui Jamkhaneh [19]). If 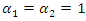 then fuzzy reliability function is as follows,
then fuzzy reliability function is as follows,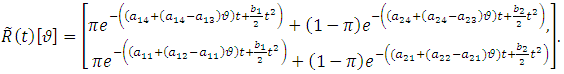 | (23) |
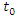 , reliability function is a fuzzy number and membership function of
, reliability function is a fuzzy number and membership function of 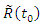 is as follows,
is as follows,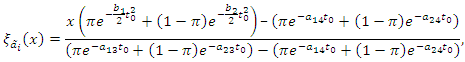 for
for 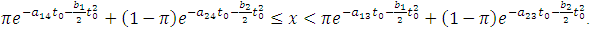
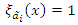 For
For 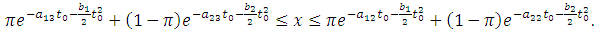
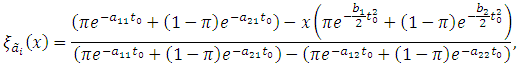 For
For 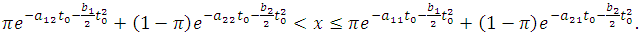 | (24) |
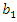 and
and 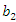 , the value of
, the value of 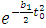 and
and 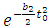 are greater than or equal to 1 and
are greater than or equal to 1 and 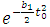 and
and 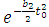 are a non-decreasing function of
are a non-decreasing function of 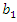 and
and 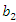 . If
. If 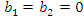 , then fuzzy number of reliability will have its maximum value with the lowest uncertainty. As the values of
, then fuzzy number of reliability will have its maximum value with the lowest uncertainty. As the values of 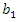 and
and 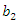 increases, we get lower values for fuzzy numbers of reliability with more uncertainty.
increases, we get lower values for fuzzy numbers of reliability with more uncertainty.5. Fuzzy Hazard Function
- Another fuzzy characterizes of the lifetime distribution is the fuzzy hazard function of two components mixture GLFRD
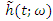 . This function is also known as the instantaneous failure rate function. We propose the concept of a fuzzy hazard function based on the fuzzy probability measure and named
. This function is also known as the instantaneous failure rate function. We propose the concept of a fuzzy hazard function based on the fuzzy probability measure and named 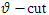 hazard band. The fuzzy hazard function of two components mixture GLFRD
hazard band. The fuzzy hazard function of two components mixture GLFRD 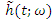 is the fuzzy conditional probability of an item failing in the short time interval t to (t + dt) given that it has not failed at time t. Mathematically, we would define the fuzzy hazard function as
is the fuzzy conditional probability of an item failing in the short time interval t to (t + dt) given that it has not failed at time t. Mathematically, we would define the fuzzy hazard function as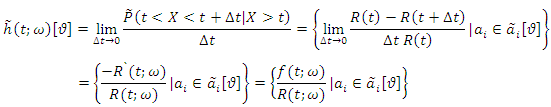 | (25) |
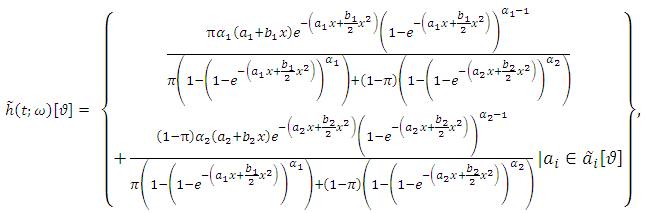 | (26) |
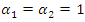 then
then | (27) |
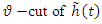 is as follows,
is as follows,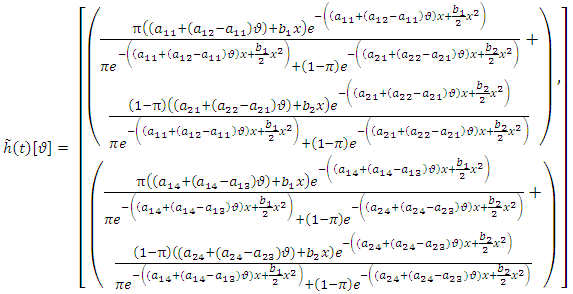 | (28) |
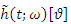 is a two dimensional function in terms of
is a two dimensional function in terms of 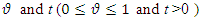 . In this method, for every
. In this method, for every 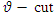 , hazard curve is like a band. One of the most important aspects of the GLFRDis performance of its hazard band. This band with change the parameters of density function can decrease, increase and be constant. For
, hazard curve is like a band. One of the most important aspects of the GLFRDis performance of its hazard band. This band with change the parameters of density function can decrease, increase and be constant. For 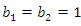 , hazard function is a fuzzy number constant for every t, whereas
, hazard function is a fuzzy number constant for every t, whereas 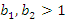 , leads to an increasing band, and hence can be considered to model wear-out, as often deemed appropriate for mechanical units, and
, leads to an increasing band, and hence can be considered to model wear-out, as often deemed appropriate for mechanical units, and 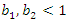 leads to decreasing band, hence modeling wear-in of a product as often advocated for electronic units. An increasing hazard band at time t indicates fuzzy failure probability of component in time (t, t + dt) is more than fuzzy failure probability the previous period the same length, that is, components wear during the time.
leads to decreasing band, hence modeling wear-in of a product as often advocated for electronic units. An increasing hazard band at time t indicates fuzzy failure probability of component in time (t, t + dt) is more than fuzzy failure probability the previous period the same length, that is, components wear during the time.6. Conclusions
- In this paper, we have studied the mixture generalized linear failure rate distribution (or MGLFRD) and discussed some statistical properties of the MGLFRD. The fuzzy reliability function and fuzzy hazard function have been successfully investigated in this paper. Whenever the lifetimes of components and parameters contain randomness and fuzziness respectively, the approach of reliability theory based on traditional statistical analysis may be inappropriate. Fuzzy system reliability is based on the concept of fuzzy set and fuzzy probability theory in our method.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML