B. S. Biradar1, Santosha C. D.2
1Department of Studies in Statistics, University of Mysore, Mysore, India
2All India Institute of Speech and Hearing, Mysore, India
Correspondence to: B. S. Biradar, Department of Studies in Statistics, University of Mysore, Mysore, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper is concerned with ranked set sampling theory which is useful to estimate the population mean when the order of a sample of small size can be found without measurements or with other methods. In practice ranking a sample of moderate size and observing the i-th ranked unit (ranking of middle ordered units) is a difficult task. Therefore, in this paper we propose two estimators of the population mean based on extremes ranked set sampling methods. The proposed estimators are unbiased for the population mean when the underlying distribution is symmetric. It is shown that the proposed estimators are more efficient than their counter part simple random sampling method for distributions considered in this study.
Keywords:
Ranked set sampling, Extremes ranked set sampling, Population mean, Relative efficiency, Errors in Ranking
Cite this paper: B. S. Biradar, Santosha C. D., Estimation of the Population Mean Based on Extremes Ranked Set Sampling, American Journal of Mathematics and Statistics, Vol. 5 No. 1, 2015, pp. 32-36. doi: 10.5923/j.ajms.20150501.05.
1. Introduction
Ranked set sampling (RSS) was introduced by McIntyre [1] (reprinted in [2]) for estimating the pasture and forage yields. McIntyre indicates that RSS is a more efficient sampling method than simple random sampling (SRS) method for estimating the population mean. It is appropriate for situations where quantification of sampling units is either costly or difficult, but ranking the units in a small set is easy and inexpensive. Ranking can be performed based on expert judgment, visual inspection or any means that does not involve actually quantifying the observations. In RSS one first draws 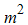 units at random from the population and partitions them into m sets of m units. The m units in each set are ranked without making actual measurements. From the first set of m units the unit ranked lowest is chosen for actual quantification. From the second set of m units the unit ranked second lowest is measured. The process is continued until the unit ranked largest is measured from the m-th set of m units. If a larger sample size is required then the procedure can be repeated r times to obtain a sample of size n = rm. These chosen elements are called a ranked set sample. Takashi and Wakimoto [3] established a very important statistical foundation for the theory of RSS. They proved that the sample mean of the RSS is an unbiased estimator of the population mean with smaller variance than the sample mean of a SRS with the same sample size. Dell and Clutter [4] showed that the mean of the RSS is an unbiased estimator of the population mean, whether or not there are errors in ranking and more efficient than the mean of SRS. Stokes [5] showed that the estimator of the variance based on RSS is an asymptotically unbiased estimator of the population variance, and it is more efficient than the usual estimator based on SRS data with same sample size, when the sample size is large. Stokes and Sager [6] studied the empirical distribution function based on RSS and showed that it is an unbiased estimate of the underlying distribution function. A recent summaries of RSS literature appear in two survey articles by Wolfe [7] and [8] and a monograph by Chen et al. [9]. Samawi et al. [10] used extreme ranked set sample(ERSS) in case of even sample size which is easier to use than the usual RSS procedure to estimate the population mean. Muttlak [11] proposed the use of median ranked set sampling (MRSS) method for estimating the population mean. Muttlak [12] investigated quartile ranked set sampling (QRSS) for estimating the population mean. Jemain et al. [13] suggested balanced groups ranked set sampling (BGRSS) for estimating population mean. These procedure are based on ranking the i-th unit (other than the extremes) of the sample which is a difficult task. Recently, Balci et al. [14] introduced another RSS based on extremes for both even and odd sample sizes. They have studied modified maximum likelihood estimator (MMLE) and Best linear unbiased estimator (BLUE) when the underlying distribution is normal. In this paper another modification RSS is introduced namely independent extreme ranked set sampling (IERSS) in the case of both even and odd sample sizes. The main objective of this paper is to propose nonparametric estimators of the population mean using these two extremes RSS and are compared with estimator based on SRS method. Since it is not difficult to identify maximum or minimum units, extremes RSS is a very useful modification of RSS. It allows for an increase in set size without introducing too many ranking errors.
units at random from the population and partitions them into m sets of m units. The m units in each set are ranked without making actual measurements. From the first set of m units the unit ranked lowest is chosen for actual quantification. From the second set of m units the unit ranked second lowest is measured. The process is continued until the unit ranked largest is measured from the m-th set of m units. If a larger sample size is required then the procedure can be repeated r times to obtain a sample of size n = rm. These chosen elements are called a ranked set sample. Takashi and Wakimoto [3] established a very important statistical foundation for the theory of RSS. They proved that the sample mean of the RSS is an unbiased estimator of the population mean with smaller variance than the sample mean of a SRS with the same sample size. Dell and Clutter [4] showed that the mean of the RSS is an unbiased estimator of the population mean, whether or not there are errors in ranking and more efficient than the mean of SRS. Stokes [5] showed that the estimator of the variance based on RSS is an asymptotically unbiased estimator of the population variance, and it is more efficient than the usual estimator based on SRS data with same sample size, when the sample size is large. Stokes and Sager [6] studied the empirical distribution function based on RSS and showed that it is an unbiased estimate of the underlying distribution function. A recent summaries of RSS literature appear in two survey articles by Wolfe [7] and [8] and a monograph by Chen et al. [9]. Samawi et al. [10] used extreme ranked set sample(ERSS) in case of even sample size which is easier to use than the usual RSS procedure to estimate the population mean. Muttlak [11] proposed the use of median ranked set sampling (MRSS) method for estimating the population mean. Muttlak [12] investigated quartile ranked set sampling (QRSS) for estimating the population mean. Jemain et al. [13] suggested balanced groups ranked set sampling (BGRSS) for estimating population mean. These procedure are based on ranking the i-th unit (other than the extremes) of the sample which is a difficult task. Recently, Balci et al. [14] introduced another RSS based on extremes for both even and odd sample sizes. They have studied modified maximum likelihood estimator (MMLE) and Best linear unbiased estimator (BLUE) when the underlying distribution is normal. In this paper another modification RSS is introduced namely independent extreme ranked set sampling (IERSS) in the case of both even and odd sample sizes. The main objective of this paper is to propose nonparametric estimators of the population mean using these two extremes RSS and are compared with estimator based on SRS method. Since it is not difficult to identify maximum or minimum units, extremes RSS is a very useful modification of RSS. It allows for an increase in set size without introducing too many ranking errors.
2. Estimation of Population Mean Based on Two New RSS
In this study two new estimators of population mean based on modified ranked set sampling methods (i) choosing both extremes of each sample and (ii) choosing extreme form two independent samples have been developed.
2.1. Ranked Set Sampling by Choosing Extremes of Samples (RSS(E))
Balci et al. [14] introduced ranked set sample by choosing extremes of the samples and they have called this sampling scheme as RSS(E). The procedure of RSS(E) is described as follows:1. Select m random samples each of size m.2. Each sample is ranked in itself as in ranked set sampling design. 3. Then smallest and largest order statistics from each sample are observed.4. Repeat above steps r times until the desired sample size n = 2rm is obtained. We assume that the lowest and largest units of this set can be detected visually, or by any other means easily. Let 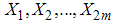 be a random sample of size 2m with probability density function f(x) with mean
be a random sample of size 2m with probability density function f(x) with mean 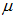 and variance
and variance 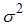 . Let
. Let 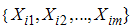 , i=1,2,…m be m sets of independent random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean
, i=1,2,…m be m sets of independent random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean 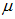 and variance
and variance 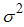 . Denote
. Denote 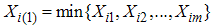 and
and 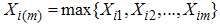 i=1,2,…,m. Then
i=1,2,…,m. Then 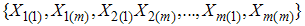 is a RSS(E) of size 2m. Note that the order statistics within the sample are dependent and between the samples are independent. For all i = 1,2,…,m let
is a RSS(E) of size 2m. Note that the order statistics within the sample are dependent and between the samples are independent. For all i = 1,2,…,m let 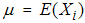 ,
, 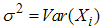 ,
, 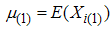 ,
, 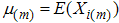 ,
, 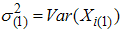 ,
, 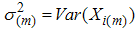 an
an 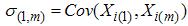 . Let
. Let 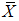 be the mean of the SRS of size 2m. The mean and variance of
be the mean of the SRS of size 2m. The mean and variance of 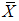 are
are 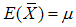 and
and 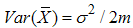 , respectively. The estimator of the population mean based on RSS(E) can be defined as
, respectively. The estimator of the population mean based on RSS(E) can be defined as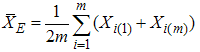 | (1) |
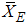 can be written as
can be written as 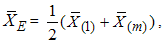 where
where 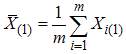 and
and 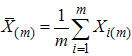 .The mean and variance of
.The mean and variance of 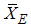 can be shown to be
can be shown to be 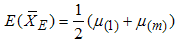 | (2) |
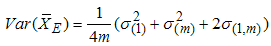 | (3) |
If the underlying distribution is symmetric about zero, then 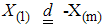 . Arnold et al. [15] have shown that
. Arnold et al. [15] have shown that 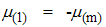 and
and 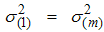 . Using these results
. Using these results 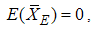 and
and 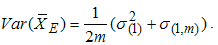 | (4) |
Thus, if the underlying distribution is symmetric about its mean then 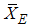 is an unbiased estimator of the population mean.
is an unbiased estimator of the population mean.
2.2. Ranked Set Sampling by Choosing Extremes of Tow Independent Samples (IERSS)
Here we introduce another modified RSS called independent Extremes ranked set sampling (IERSS) based on two independent samples of size 2m: first we select 2m random samples of size m each and then identify the maximum within each set of first m samples by visual inspection or by some other cheap method, without actual measurement of the variable of interest. Repeat this for other m simple random samples but for the minima. Repeat above steps for r times until the desired sample size n=2rm is obtained. Let 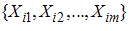 and
and 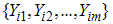 i=1,2,…m be 2m sets of random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean
i=1,2,…m be 2m sets of random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean 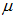 and variance
and variance 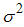 . Denote
. Denote 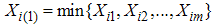 and
and 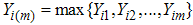 , i=1,2,…,m. Then
, i=1,2,…,m. Then 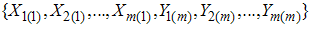 be IERSS of size 2m. Note that elements of sample are independent of each other. The estimator of the population mean based on IERSS with one cycle can be defined as:
be IERSS of size 2m. Note that elements of sample are independent of each other. The estimator of the population mean based on IERSS with one cycle can be defined as: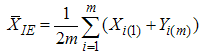 | (5) |
The mean and variance of 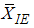 can be shown to be
can be shown to be 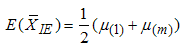 | (6) |
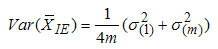 | (7) |
Where 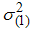 is as defined above and
is as defined above and 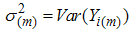 . If the underlying distribution is symmetric about zero then using the above results of Arnold et al.(1992) , we have
. If the underlying distribution is symmetric about zero then using the above results of Arnold et al.(1992) , we have 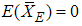 and
and 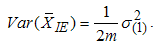 | (8) |
We can easily see that if the underlying distribution is symmetric about its mean then 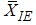 is an unbiased estimator of the population mean.
is an unbiased estimator of the population mean.
3. Efficiency
The efficiency of 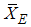 with respect to
with respect to 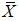 for estimating the population mean is defined as:
for estimating the population mean is defined as: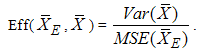 | (9) |
If the distribution is symmetric then 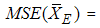
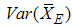 .Similarly,
.Similarly,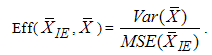 | (10) |
If the distribution is symmetric then 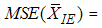
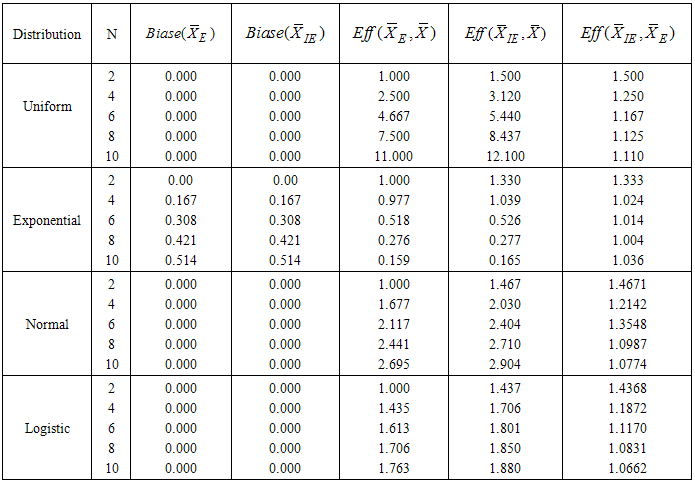
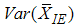 .And finally
.And finally 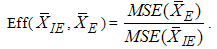 | (11) |
For uniform distribution over (0,1) the efficiency of 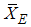 with respect to
with respect to 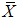 is given by
is given by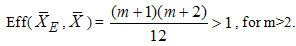 | (12) |
Similarly the efficiency of 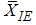 with respect to
with respect to 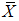 is given by
is given byTable 1. The Relative Efficiency of estimators of population mean using RSS(E) and IERSS
 |
| |
|
 , for m>1 and tends to 1 as m goes to infinity. This indicates that as the set size m increases
, for m>1 and tends to 1 as m goes to infinity. This indicates that as the set size m increases  tends to zero and both estimators
tends to zero and both estimators 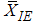 and
and 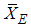 are equally efficient. The results of efficiency and bias of the estimators are presented in Table 1 for uniform, exponential, normal and logistic distributions using SRS, RSSE and IERSS sampling schemes. From Table 1 we observed that in the case of uniform, normal and logistic distributions the estimators based on
are equally efficient. The results of efficiency and bias of the estimators are presented in Table 1 for uniform, exponential, normal and logistic distributions using SRS, RSSE and IERSS sampling schemes. From Table 1 we observed that in the case of uniform, normal and logistic distributions the estimators based on 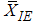 and
and 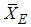 are both more efficient than
are both more efficient than 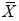 and
and 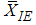 is more efficient than
is more efficient than 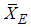 . For exponential distribution
. For exponential distribution 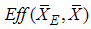 and
and 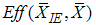 decrease as m increases. This is because
decrease as m increases. This is because 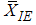 and
and 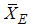 are bias estimators and bias diverges as m goes to
are bias estimators and bias diverges as m goes to 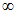 . We can easily see that the estimator of population mean based on
. We can easily see that the estimator of population mean based on 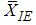 is equivalent to the one of the estimators proposed by Samawi et al. [10] based on extreme ranked set sample with number of cycles equal two and when set size m is even.
is equivalent to the one of the estimators proposed by Samawi et al. [10] based on extreme ranked set sample with number of cycles equal two and when set size m is even.
4. Extreme RSS with Errors in Ranking
Dell and Clutter [4] considered the case in which there are errors in ranking; that is , the quantified observation from the i-th sample in the j-th cycle may no be the i-th order statistic but rather the i-th judgement order statistic. They showed that the sample mean of RSS with errors in ranking is unbiased estimator of the population mean regardless of the errors in ranking and has smaller variance than the usual estimator based on SRS with the same sample size.Let 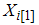 and
and 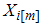 denote the smallest and largest judgment order statistic of the sample respectively (i=1,2,…,m) . Then
denote the smallest and largest judgment order statistic of the sample respectively (i=1,2,…,m) . Then 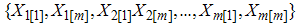 and
and 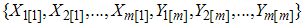 denote RSS(E) and IERSS samples with errors in ranking. The estimators of the population mean using RSS(E) and IERSS with errors in ranking can be defined as
denote RSS(E) and IERSS samples with errors in ranking. The estimators of the population mean using RSS(E) and IERSS with errors in ranking can be defined as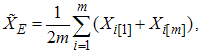 | (13) |
and 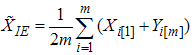 | (14) |
The variance of 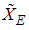 and
and 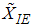 can be defined as
can be defined as 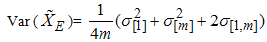 | (15) |
and 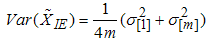 | (16) |
where 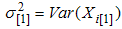 ,
, 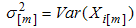 and
and 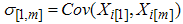 for i=1,2,…m.It can easily seen that
for i=1,2,…m.It can easily seen that 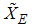 and
and 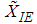 are unbiased estimators of the population mean if the underlying distribution is symmetric about its mean.
are unbiased estimators of the population mean if the underlying distribution is symmetric about its mean.
5. Conclusions
We proposed two new estimators of the population mean using two modified ranked set sampling methods. The proposed estimators are unbiased of the population mean when the underlying distribution is symmetric about its mean. We showed that both estimators have smaller variances than the estimator using SRS and provide more efficient estimators. The estimators using extremes RSS (RSS (E) and IERSS) will reduce errors in ranking compared to RSS, MRSS, QRSS and BGRSS, since we have to identify and measure the smallest and largest of the ith sample.
ACKNOWLEDGEMENTS
The Authors are very grateful to the referee and editor for their thoughtful comments and suggestions.
References
| [1] | McIntyre, G.A. (1952). A method for unbiased selective sampling using ranked sets.Aust.J Agri.Res.3:385-390. |
| [2] | McIntyre, G.A., (2005). A method for unbiased selective sampling, using ranked sets. The American Statistician 59, 230–232. Originally appeared in Australian Journal of Agricultural Research 3, 385–390. |
| [3] | Takahasi, K. and Wakimoto, K. (1968). On unbiased estimates of the population mean based on the sample stratified by means of ordering. Ann. Inst. Stat. Math., 20, 1-31. |
| [4] | Dell, T.R. and Clutter, J.L. (1972). Ranked Set Sampling Theory with Order Statistics Background. Biometrics, 28, 545-555. |
| [5] | Stokes, S.L. (1980) Estimation of variance using judgment ordered ranked set samples, Biometrics,36,35-42. |
| [6] | Stokes, S.L and Sager, T. (1988). Characterization of a ranked set sample with application to estimating distribution functions, J.Amer.Statist.Assoc., 83, 374-381. |
| [7] | Wolfe, D.A. (2004). Ranked set sampling: an approach to more efficient data collection. Statistical Science 19, 636–643. |
| [8] | Wolfe, D.A., (2010). Ranked set sampling. Wiley Interdisciplinary Reviews: Computational Statistics 2, 460–466. |
| [9] | Chen, Z., Bai, Z., Sinha, B.K., (2004). Ranked Set Sampling: Theory and Applications. Springer, New York. |
| [10] | Samwi, H., Ahmad, M. and Abu-Dayyeh, W. (1996). Estimating the population mean using extreme ranked set sampling. Biom. Journal, 38, 577-586. |
| [11] | Muttlak, H.A (1997) Median Ranked set sampling, Journal of applied statistical Sciences,6,245-255. |
| [12] | Muttlak H.A. (2003). Investigating the use of quartile ranked set samples for estimating the population mean. Journal of Applied Mathematics and Computation.146,437-443. |
| [13] | Jemain A.A., Al-omari A, Ibrahim, K (2008). Some variations of Ranked set samling. Electronic J.App. Stat. Anal., 1, 1-15. |
| [14] | Balci, S, Akkaya A.D., Ulgen, B.E (2013) Modified Maximum Likelihood estimators using ranked set sampling. Journal of Computational and Applied Mathematics 238,171-179. |
| [15] | Arnold, B.C. Balkrishna, N and Nagaraj, H.N. (1992). A First course in oreder statistics. John Wiley and Sons, New York. |

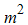 units at random from the population and partitions them into m sets of m units. The m units in each set are ranked without making actual measurements. From the first set of m units the unit ranked lowest is chosen for actual quantification. From the second set of m units the unit ranked second lowest is measured. The process is continued until the unit ranked largest is measured from the m-th set of m units. If a larger sample size is required then the procedure can be repeated r times to obtain a sample of size n = rm. These chosen elements are called a ranked set sample. Takashi and Wakimoto [3] established a very important statistical foundation for the theory of RSS. They proved that the sample mean of the RSS is an unbiased estimator of the population mean with smaller variance than the sample mean of a SRS with the same sample size. Dell and Clutter [4] showed that the mean of the RSS is an unbiased estimator of the population mean, whether or not there are errors in ranking and more efficient than the mean of SRS. Stokes [5] showed that the estimator of the variance based on RSS is an asymptotically unbiased estimator of the population variance, and it is more efficient than the usual estimator based on SRS data with same sample size, when the sample size is large. Stokes and Sager [6] studied the empirical distribution function based on RSS and showed that it is an unbiased estimate of the underlying distribution function. A recent summaries of RSS literature appear in two survey articles by Wolfe [7] and [8] and a monograph by Chen et al. [9]. Samawi et al. [10] used extreme ranked set sample(ERSS) in case of even sample size which is easier to use than the usual RSS procedure to estimate the population mean. Muttlak [11] proposed the use of median ranked set sampling (MRSS) method for estimating the population mean. Muttlak [12] investigated quartile ranked set sampling (QRSS) for estimating the population mean. Jemain et al. [13] suggested balanced groups ranked set sampling (BGRSS) for estimating population mean. These procedure are based on ranking the i-th unit (other than the extremes) of the sample which is a difficult task. Recently, Balci et al. [14] introduced another RSS based on extremes for both even and odd sample sizes. They have studied modified maximum likelihood estimator (MMLE) and Best linear unbiased estimator (BLUE) when the underlying distribution is normal. In this paper another modification RSS is introduced namely independent extreme ranked set sampling (IERSS) in the case of both even and odd sample sizes. The main objective of this paper is to propose nonparametric estimators of the population mean using these two extremes RSS and are compared with estimator based on SRS method. Since it is not difficult to identify maximum or minimum units, extremes RSS is a very useful modification of RSS. It allows for an increase in set size without introducing too many ranking errors.
units at random from the population and partitions them into m sets of m units. The m units in each set are ranked without making actual measurements. From the first set of m units the unit ranked lowest is chosen for actual quantification. From the second set of m units the unit ranked second lowest is measured. The process is continued until the unit ranked largest is measured from the m-th set of m units. If a larger sample size is required then the procedure can be repeated r times to obtain a sample of size n = rm. These chosen elements are called a ranked set sample. Takashi and Wakimoto [3] established a very important statistical foundation for the theory of RSS. They proved that the sample mean of the RSS is an unbiased estimator of the population mean with smaller variance than the sample mean of a SRS with the same sample size. Dell and Clutter [4] showed that the mean of the RSS is an unbiased estimator of the population mean, whether or not there are errors in ranking and more efficient than the mean of SRS. Stokes [5] showed that the estimator of the variance based on RSS is an asymptotically unbiased estimator of the population variance, and it is more efficient than the usual estimator based on SRS data with same sample size, when the sample size is large. Stokes and Sager [6] studied the empirical distribution function based on RSS and showed that it is an unbiased estimate of the underlying distribution function. A recent summaries of RSS literature appear in two survey articles by Wolfe [7] and [8] and a monograph by Chen et al. [9]. Samawi et al. [10] used extreme ranked set sample(ERSS) in case of even sample size which is easier to use than the usual RSS procedure to estimate the population mean. Muttlak [11] proposed the use of median ranked set sampling (MRSS) method for estimating the population mean. Muttlak [12] investigated quartile ranked set sampling (QRSS) for estimating the population mean. Jemain et al. [13] suggested balanced groups ranked set sampling (BGRSS) for estimating population mean. These procedure are based on ranking the i-th unit (other than the extremes) of the sample which is a difficult task. Recently, Balci et al. [14] introduced another RSS based on extremes for both even and odd sample sizes. They have studied modified maximum likelihood estimator (MMLE) and Best linear unbiased estimator (BLUE) when the underlying distribution is normal. In this paper another modification RSS is introduced namely independent extreme ranked set sampling (IERSS) in the case of both even and odd sample sizes. The main objective of this paper is to propose nonparametric estimators of the population mean using these two extremes RSS and are compared with estimator based on SRS method. Since it is not difficult to identify maximum or minimum units, extremes RSS is a very useful modification of RSS. It allows for an increase in set size without introducing too many ranking errors. 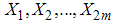 be a random sample of size 2m with probability density function f(x) with mean
be a random sample of size 2m with probability density function f(x) with mean 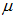 and variance
and variance 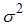 . Let
. Let 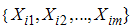 , i=1,2,…m be m sets of independent random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean
, i=1,2,…m be m sets of independent random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean 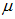 and variance
and variance 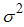 . Denote
. Denote 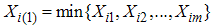 and
and 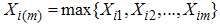 i=1,2,…,m. Then
i=1,2,…,m. Then 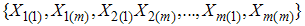 is a RSS(E) of size 2m. Note that the order statistics within the sample are dependent and between the samples are independent. For all i = 1,2,…,m let
is a RSS(E) of size 2m. Note that the order statistics within the sample are dependent and between the samples are independent. For all i = 1,2,…,m let 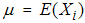 ,
, 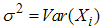 ,
, 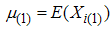 ,
, 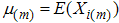 ,
, 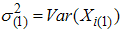 ,
, 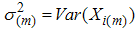 an
an 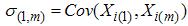 . Let
. Let 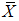 be the mean of the SRS of size 2m. The mean and variance of
be the mean of the SRS of size 2m. The mean and variance of 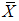 are
are 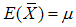 and
and 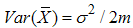 , respectively. The estimator of the population mean based on RSS(E) can be defined as
, respectively. The estimator of the population mean based on RSS(E) can be defined as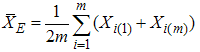
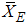 can be written as
can be written as 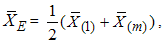 where
where 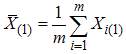 and
and 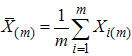 .The mean and variance of
.The mean and variance of 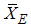 can be shown to be
can be shown to be 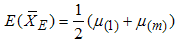
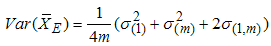
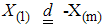 . Arnold et al. [15] have shown that
. Arnold et al. [15] have shown that 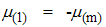 and
and 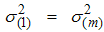 . Using these results
. Using these results 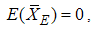 and
and 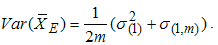
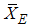 is an unbiased estimator of the population mean.
is an unbiased estimator of the population mean. 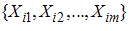 and
and 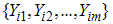 i=1,2,…m be 2m sets of random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean
i=1,2,…m be 2m sets of random samples each of size m from a population with distribution function F(x) and pdf f(x) with mean 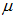 and variance
and variance 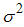 . Denote
. Denote 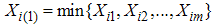 and
and 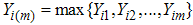 , i=1,2,…,m. Then
, i=1,2,…,m. Then 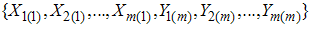 be IERSS of size 2m. Note that elements of sample are independent of each other. The estimator of the population mean based on IERSS with one cycle can be defined as:
be IERSS of size 2m. Note that elements of sample are independent of each other. The estimator of the population mean based on IERSS with one cycle can be defined as: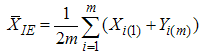
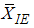 can be shown to be
can be shown to be 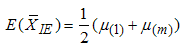
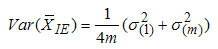
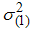 is as defined above and
is as defined above and 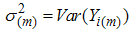 . If the underlying distribution is symmetric about zero then using the above results of Arnold et al.(1992) , we have
. If the underlying distribution is symmetric about zero then using the above results of Arnold et al.(1992) , we have 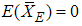 and
and 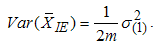
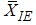 is an unbiased estimator of the population mean.
is an unbiased estimator of the population mean. 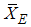 with respect to
with respect to 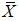 for estimating the population mean is defined as:
for estimating the population mean is defined as: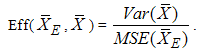
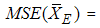
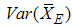 .Similarly,
.Similarly,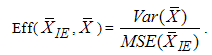
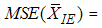
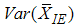 .And finally
.And finally 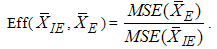
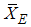 with respect to
with respect to 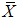 is given by
is given by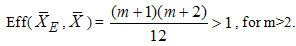
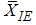 with respect to
with respect to 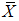 is given by
is given by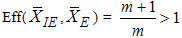 , for m>1 and tends to 1 as m goes to infinity. This indicates that as the set size m increases
, for m>1 and tends to 1 as m goes to infinity. This indicates that as the set size m increases 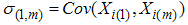 tends to zero and both estimators
tends to zero and both estimators 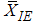 and
and 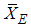 are equally efficient. The results of efficiency and bias of the estimators are presented in Table 1 for uniform, exponential, normal and logistic distributions using SRS, RSSE and IERSS sampling schemes. From Table 1 we observed that in the case of uniform, normal and logistic distributions the estimators based on
are equally efficient. The results of efficiency and bias of the estimators are presented in Table 1 for uniform, exponential, normal and logistic distributions using SRS, RSSE and IERSS sampling schemes. From Table 1 we observed that in the case of uniform, normal and logistic distributions the estimators based on 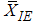 and
and 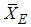 are both more efficient than
are both more efficient than 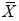 and
and 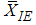 is more efficient than
is more efficient than 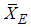 . For exponential distribution
. For exponential distribution 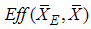 and
and 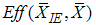 decrease as m increases. This is because
decrease as m increases. This is because 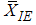 and
and 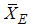 are bias estimators and bias diverges as m goes to
are bias estimators and bias diverges as m goes to 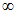 . We can easily see that the estimator of population mean based on
. We can easily see that the estimator of population mean based on 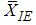 is equivalent to the one of the estimators proposed by Samawi et al. [10] based on extreme ranked set sample with number of cycles equal two and when set size m is even.
is equivalent to the one of the estimators proposed by Samawi et al. [10] based on extreme ranked set sample with number of cycles equal two and when set size m is even. 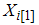 and
and 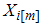 denote the smallest and largest judgment order statistic of the sample respectively (i=1,2,…,m) . Then
denote the smallest and largest judgment order statistic of the sample respectively (i=1,2,…,m) . Then 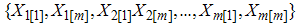 and
and 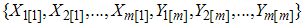 denote RSS(E) and IERSS samples with errors in ranking. The estimators of the population mean using RSS(E) and IERSS with errors in ranking can be defined as
denote RSS(E) and IERSS samples with errors in ranking. The estimators of the population mean using RSS(E) and IERSS with errors in ranking can be defined as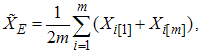
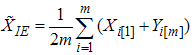
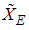 and
and 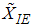 can be defined as
can be defined as 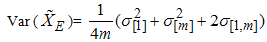
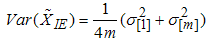
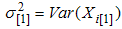 ,
, 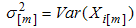 and
and 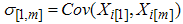 for i=1,2,…m.It can easily seen that
for i=1,2,…m.It can easily seen that 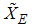 and
and 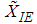 are unbiased estimators of the population mean if the underlying distribution is symmetric about its mean.
are unbiased estimators of the population mean if the underlying distribution is symmetric about its mean. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML