Stephen Ehidiamhen Uwamusi
Department of Mathematical Sciences, Kogi State University, Anyigba, Nigeria
Correspondence to: Stephen Ehidiamhen Uwamusi , Department of Mathematical Sciences, Kogi State University, Anyigba, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The paper discusses the graph completion inclusion isotone for interval least squares problem wherein, incorporated the Tikhonov regularization for resolving the recurrent problem of ill-conditioning for the resulting interval linear least squares using quadratic polynomial fit. It is established that convergence of interval operators to the described interval least squares problems implies convergence in the tempered distribution of interval data in the sense of [2]. The open Question of Completeness of graph in Banach Space Topology is addressed and estimate of eigenvalues to the interval matrix was given further interpretation using ideas of [24] which has great importance in the study of growth rate of a system. Numerical example is demonstrated with described methods.
Keywords:
Least squares problem, Graph inclusion isotone, Banach space, Tempered distribution, Circular interval arithmetic, Interval matrix eigenvalues
Cite this paper: Stephen Ehidiamhen Uwamusi , Graph Completion Inclusion Isotone for Interval Least Squares Equation, American Journal of Mathematics and Statistics, Vol. 5 No. 1, 2015, pp. 24-31. doi: 10.5923/j.ajms.20150501.04.
1. Introduction
The paper considers graph completion inclusion isotone for least squares problem with uncertain data. The closed graph theorem in the sense of [1], and [2] for instance gives a basic result that characterizes continuous functions in terms of their graphs. For any function 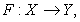 we define the graph
we define the graph 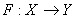 , as the map
, as the map 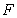 to be the Cartessian product
to be the Cartessian product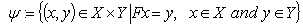 .There is a metric topology for which is defined
.There is a metric topology for which is defined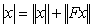 . When
. When 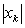 is Cauchy, for
is Cauchy, for 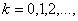 it follows that
it follows that 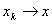 in
in 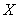 as
as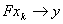 . In other words, for a closed graph F, it holds that
. In other words, for a closed graph F, it holds that 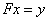 forcing
forcing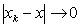 implying the graph of
implying the graph of 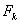 is enclosed by the convex hull of control points. In a nutshell, a graph
is enclosed by the convex hull of control points. In a nutshell, a graph 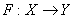 is continuous at the point
is continuous at the point 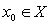 if it pulls open sets back to open sets and carries open sets over to open sets.Fundamental to this discussion are the basic principles of advanced topology. Good reference texts may be [1], [3] and [4]. Following [1], a linear map F from a linear topological space X to a linear topological space Y will be called bounded if it maps bounded sets to bounded sets. A map which is a linear topological space X to a linear topological space Y will be called sequentially continuous if for every sequence
if it pulls open sets back to open sets and carries open sets over to open sets.Fundamental to this discussion are the basic principles of advanced topology. Good reference texts may be [1], [3] and [4]. Following [1], a linear map F from a linear topological space X to a linear topological space Y will be called bounded if it maps bounded sets to bounded sets. A map which is a linear topological space X to a linear topological space Y will be called sequentially continuous if for every sequence 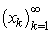 converging to some point x of E has a bounded envelope and such a sequentially continuous map is ultrabarrelled [1]. A function F is called approxable in the sense of [5] if for a multi valued mapping
converging to some point x of E has a bounded envelope and such a sequentially continuous map is ultrabarrelled [1]. A function F is called approxable in the sense of [5] if for a multi valued mapping 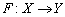 for every
for every 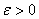 there is continuous single valued mapping
there is continuous single valued mapping 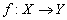 with graph
with graph 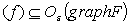 . A function
. A function 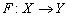 is said to be upper semi-continuous at
is said to be upper semi-continuous at 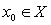 if for any neighbourhood
if for any neighbourhood 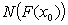 of
of 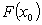 there exists a neighbourhood
there exists a neighbourhood 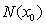 of
of 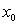 such that
such that 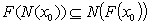 . A similar definition goes for a lower semi continuous function.By reasons due to recurrence and category theorem, the map
. A similar definition goes for a lower semi continuous function.By reasons due to recurrence and category theorem, the map 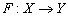 has a measure preserving homeomorphism and hence its set of recurrent point is residual and of full measure. In other words it can be said that such a map has a generic measure preserving homeomorphism whose square has a dense orbit. In some cases one often comes across some functions with distortions at some points which necessitate the following definition.Definition 1.1, [6]. Let
has a measure preserving homeomorphism and hence its set of recurrent point is residual and of full measure. In other words it can be said that such a map has a generic measure preserving homeomorphism whose square has a dense orbit. In some cases one often comes across some functions with distortions at some points which necessitate the following definition.Definition 1.1, [6]. Let 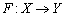 be a map between two locally Euclidean metric spaces. The quantity
be a map between two locally Euclidean metric spaces. The quantity 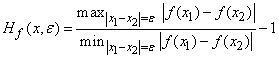 , is called the radius
, is called the radius 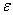 distortion of
distortion of 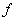 at x.As a consequence following, we introduce the nonlinear system of equation
at x.As a consequence following, we introduce the nonlinear system of equation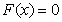 | (1.1) |
where 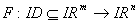 , m>n,
, m>n, 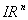 is an interval vector. It is supposed that the function F has at least
is an interval vector. It is supposed that the function F has at least 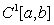 where
where 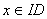 . Therefore, in a Frechet space E, every continuous linear map from a Frechet space E into F has a closed range and such a map is finite dimensional. Applications of nonlinear systems for example are well documented in the work of [7] which includes the following: Aircraft stability problems, Inverse Elastic rod problems, Equations of radiative transfer, Elliptic boundary value problems, Power flow problems, Distribution of water on a pipeline, Discretization of evolution problems using implicit schemes, Chemical plant equilibrium problems and, Nonlinear programming problems. We often adopt the concept of divided difference from a univariate function which is extended over to multivariate vector valued function by defining slope as
. Therefore, in a Frechet space E, every continuous linear map from a Frechet space E into F has a closed range and such a map is finite dimensional. Applications of nonlinear systems for example are well documented in the work of [7] which includes the following: Aircraft stability problems, Inverse Elastic rod problems, Equations of radiative transfer, Elliptic boundary value problems, Power flow problems, Distribution of water on a pipeline, Discretization of evolution problems using implicit schemes, Chemical plant equilibrium problems and, Nonlinear programming problems. We often adopt the concept of divided difference from a univariate function which is extended over to multivariate vector valued function by defining slope as 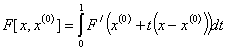 , provided that F is differentiable on the line
, provided that F is differentiable on the line 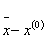 .Motivated by the above details, we state the following:Lemma 1.1, [8]. Let
.Motivated by the above details, we state the following:Lemma 1.1, [8]. Let 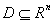 be convex and let
be convex and let 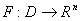 be continuously differentiable in D.(i) If
be continuously differentiable in D.(i) If 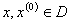 then
then 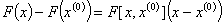 (This is a strong form of Mean-value theorem);(ii) if
(This is a strong form of Mean-value theorem);(ii) if 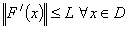 then
then 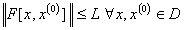 and
and 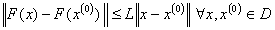 (This is a weak form of Mean-value theorem);(iii) if
(This is a weak form of Mean-value theorem);(iii) if 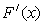 is Lipschitz continuous in D, that is the relation
is Lipschitz continuous in D, that is the relation 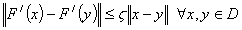 holds for some
holds for some 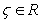 , then
, then 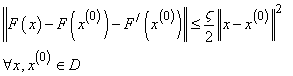 (This is truncated Taylor expansion with remainder term).It is a result to follow up to the discussion that we have the following theorems.Theorem 1.1, [9]. Suppose
(This is truncated Taylor expansion with remainder term).It is a result to follow up to the discussion that we have the following theorems.Theorem 1.1, [9]. Suppose 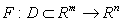 has an F-derivative at each point of an open neighbourhood of
has an F-derivative at each point of an open neighbourhood of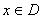 . Then,
. Then, 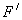 is strong at x if and only if
is strong at x if and only if 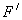 is continuous at
is continuous at 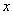 .Because system 1.1 is over determined, we often transform to a linear system by the process of 2-norm assuming that the Jacobian matrix
.Because system 1.1 is over determined, we often transform to a linear system by the process of 2-norm assuming that the Jacobian matrix 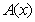 which is rectangular exists in the form
which is rectangular exists in the form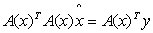 | (1.2) |
This operator is required to be everywhere defined that also holds verbatim in Banach space, provided its graph 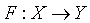 is closed in
is closed in 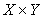 with respect to its product topology.Of paramount interest to us is a mapping that is balanced and absorbent whose inductive limit is ultra barrelled for which contraction mapping of Newton-Mysovskii theorem follows: Theorem 1.2, [9]. Supposing that
with respect to its product topology.Of paramount interest to us is a mapping that is balanced and absorbent whose inductive limit is ultra barrelled for which contraction mapping of Newton-Mysovskii theorem follows: Theorem 1.2, [9]. Supposing that 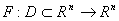 is F-differentiable on a convex set
is F-differentiable on a convex set 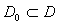 and that for each
and that for each 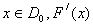 is non-singular and satisfies
is non-singular and satisfies 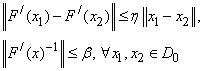 . Assuming further that
. Assuming further that 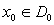 such that
such that 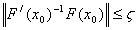 ;
; 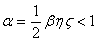 and
and 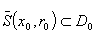 for which
for which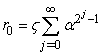 . Then the iterated contraction of Newton operator is in the form:
. Then the iterated contraction of Newton operator is in the form: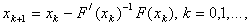 | (1.3) |
which remains in 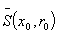 and converges to a solution
and converges to a solution 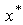 of
of 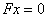 .Moreover,
.Moreover,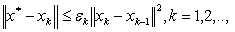 where
where 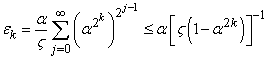 .We expect the weak pre-image
.We expect the weak pre-image 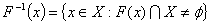 and the strong pre-image
and the strong pre-image 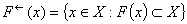 coincide simultaneously such that the orbit of F is a sequence
coincide simultaneously such that the orbit of F is a sequence 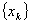 for which
for which 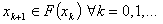 | (1.4) |
holds good that 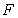 be coercive and a local homeomorphism of
be coercive and a local homeomorphism of 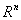 to itself, every zero of
to itself, every zero of 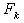 is in the intersection of convex hull with the hyper plane
is in the intersection of convex hull with the hyper plane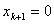 .As a result of equation 1.4 the norm reducing property of Newton operator for system 1.1 is given by
.As a result of equation 1.4 the norm reducing property of Newton operator for system 1.1 is given by 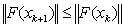 for k=0,1,.., .The quantity
for k=0,1,.., .The quantity 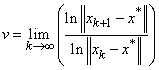 will be called the order of convergence for
will be called the order of convergence for 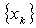 assuming the limit exists which is again equal to the R-Order of convergence of [9].The rest part in the paper is arranged as follows: Section 2 discusses what is meant by the statistical meaning of the matrix
assuming the limit exists which is again equal to the R-Order of convergence of [9].The rest part in the paper is arranged as follows: Section 2 discusses what is meant by the statistical meaning of the matrix 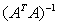 . Section 3 describes completeness of graph in Banach space topology. Procedure for estimating eigenvalues of interval Jacobian matrix formed the basis of discussion in chapter 4. Section 5 in the paper gives numerical illustration of what has been discussed in previous sections.
. Section 3 describes completeness of graph in Banach space topology. Procedure for estimating eigenvalues of interval Jacobian matrix formed the basis of discussion in chapter 4. Section 5 in the paper gives numerical illustration of what has been discussed in previous sections.
2. The Statistical Meaning of the Matrix 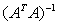 and Its Applications
and Its Applications
Henceforth, we adopt that the matrix A denotes the matrix A(x). In line with ideas expressed in [10] we give the statistical meaning to the matrix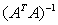 . We note that the components
. We note that the components 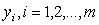 are independent, normally distributed random variable with mean
are independent, normally distributed random variable with mean 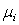 and all having the same variance
and all having the same variance 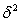 which we describe in the form:
which we describe in the form: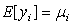 ,
, 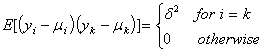 Therefore setting
Therefore setting 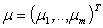 there holds that
there holds that 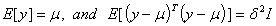 The covariance matrix of the random vector y is given by
The covariance matrix of the random vector y is given by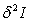 . The first moments are
. The first moments are 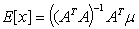 and
and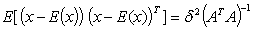 . For a rectangular matrix A for which
. For a rectangular matrix A for which 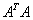 is non singular Nuemaier [11] using
is non singular Nuemaier [11] using 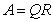 decomposition proved that
decomposition proved that 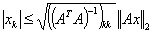 for all x.Following [12], it was proved that over any field,
for all x.Following [12], it was proved that over any field, 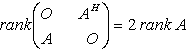 and that
and that 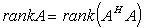 holds over any field of characteristic 0. This means computing least squares solution or bounding the errors of computations are not defined over an arbitrary field. It thus holds that
holds over any field of characteristic 0. This means computing least squares solution or bounding the errors of computations are not defined over an arbitrary field. It thus holds that 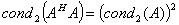 and that
and that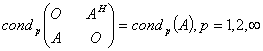 .We shall be interested in the least squares problem where the coefficient matrix and right hand vector assume some kind of noise often known as white noise. This situation leads to what is called Total Least Squares Problem (TLS) whereby, tempered distribution to the coefficient matrix A is
.We shall be interested in the least squares problem where the coefficient matrix and right hand vector assume some kind of noise often known as white noise. This situation leads to what is called Total Least Squares Problem (TLS) whereby, tempered distribution to the coefficient matrix A is , and to the vector y by
, and to the vector y by  respectively for which holds
respectively for which holds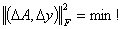 | (2.1) |
Subject to 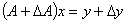 | (2.2) |
The expression 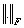 is the usual Frobenius norm which coincides with
is the usual Frobenius norm which coincides with 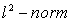 in the classical Banach space. In its simplest form, the linear inverse problem [13], [14] to which the least squares problem belongs was described in the form:
in the classical Banach space. In its simplest form, the linear inverse problem [13], [14] to which the least squares problem belongs was described in the form: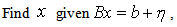 | (2.3) |
where, 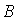 represents
represents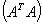 ,
, 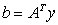 , and
, and 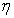 is the realization of random noise. Thus when B is invertible the linear system 2.3 is said to be well posed whereas it is ill-posed when B is not invertible.As a result the minimum
is the realization of random noise. Thus when B is invertible the linear system 2.3 is said to be well posed whereas it is ill-posed when B is not invertible.As a result the minimum 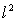 -norm of the residual is given by
-norm of the residual is given by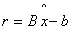 | (2.4) |
Where, it is understood that 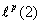 is the norm on
is the norm on 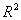 with unit ball defined by
with unit ball defined by 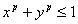 ..By substituting (2.4) into (1.1) we have that
..By substituting (2.4) into (1.1) we have that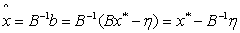 | (2.5) |
In equation 2.5, the second term 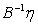 dominates in the ill-posed problem when the uncertainty is high thereby making
dominates in the ill-posed problem when the uncertainty is high thereby making  practically useless in most cases of applications. This means that the induced map
practically useless in most cases of applications. This means that the induced map 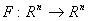 is open, nearly continuous, and nearly open if and only if
is open, nearly continuous, and nearly open if and only if 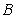 has the same ill-posed property, [1]. Therefore via interval arithmetic this problem has been addressed [15].We expect that both
has the same ill-posed property, [1]. Therefore via interval arithmetic this problem has been addressed [15].We expect that both 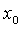 and
and 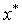 be closed in the
be closed in the 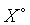 topology [1] so that,
topology [1] so that, 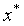 convergence implies convergence in the tempered distribution for which any neighbourhood
convergence implies convergence in the tempered distribution for which any neighbourhood 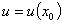 in the metric space
in the metric space 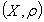 holds for
holds for 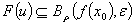 satisfying system 1.1.As pointed by some schools of thought, one drawback of Tikhonov regularization is that it tends to produce a solution that is often excessively smooth in image processing for which this method results in loss of sharpness. Nevertheless, the classical Tikhonov regularization method for minimizing
satisfying system 1.1.As pointed by some schools of thought, one drawback of Tikhonov regularization is that it tends to produce a solution that is often excessively smooth in image processing for which this method results in loss of sharpness. Nevertheless, the classical Tikhonov regularization method for minimizing 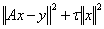 has the solution as
has the solution as 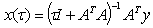 in the sense of [16]. The equation that determines
in the sense of [16]. The equation that determines 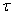 in the restructured least squares sense was given by
in the restructured least squares sense was given by 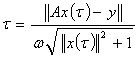 | (2.6) |
where 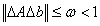 is well defined.Thus when
is well defined.Thus when 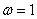 the optimal solution is given by
the optimal solution is given by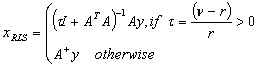 Where
Where 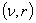 are the unique optimal point to the problem minimize
are the unique optimal point to the problem minimize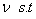
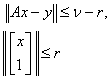 Note that
Note that 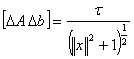 and
and 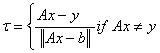 .Since
.Since 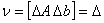 and
and  is rank one, it holds that
is rank one, it holds that 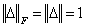 . This forces
. This forces 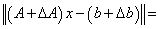
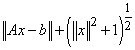 .Equation 2.6 is used when there is no perturbation in y. In case of total least squares the solution to the perturbed least squares equation 2.1 is given by the
.Equation 2.6 is used when there is no perturbation in y. In case of total least squares the solution to the perturbed least squares equation 2.1 is given by the 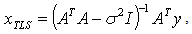 | (2.7) |
where 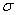 is the smallest singular value of
is the smallest singular value of 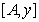 , ([ 17], e.g.,). In most applications of interest we often perturb the matrix B such that perturbation
, ([ 17], e.g.,). In most applications of interest we often perturb the matrix B such that perturbation 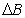 satisfies the condition that
satisfies the condition that 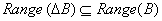 and
and 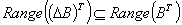 | (2.8) |
Because of equation 2.8, it follows that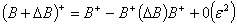 | (2.9) |
Where we used the fact that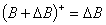 , and
, and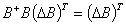 . The matrix
. The matrix 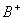 is the Pseudo-Penrose inverse of
is the Pseudo-Penrose inverse of 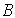 .As a result of equations 2.8 and 2.9 and in view of equation 2.7, it can be deduced that
.As a result of equations 2.8 and 2.9 and in view of equation 2.7, it can be deduced that 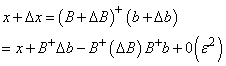 | (2.10) |
The actual value of 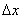 as well as
as well as 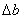 is obtained in the form
is obtained in the form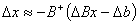 | (2.11) |
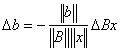 | (2.12) |
Therefore when the matrix B is perturbed by 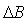 , from well known result [18] there holds the estimate
, from well known result [18] there holds the estimate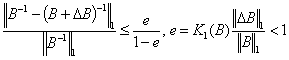 | (2.13) |
3. The Question of Completeness of graph in Banach Space Topology
We are interested in the regularity property of graph that is equated to openness which relates regularity to inversion problems. By this we mean regularity of set valued maps, [19] for which openness and inversion properties of equation 1.1 form the basis of investigation. Inverse mapping theorem asserts that the inverse of an invertible bounded linear operator between Banach spaces is a continuous map.As is well known, a complete metric space cannot be written as a countable union of nowhere dense sets. The Baire Category theorem provides that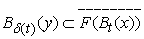 , an indication that F is open around
, an indication that F is open around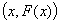 and
and 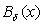 is the open
is the open 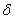 -neighbourhood of x in
-neighbourhood of x in 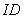 . That is,
. That is,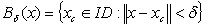 | (3.1) |
Fundamentally, what is required is the graph completion operator that is inclusion isotone with respect to functional argument. That is, the Hausdorff continuous operator 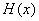 satisfying the inclusion
satisfying the inclusion 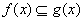 which is Dedekind order complete
which is Dedekind order complete  with respect to point wise defined partial ordering. As it were, we also assume that
with respect to point wise defined partial ordering. As it were, we also assume that 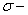 finite algebra of measurable sets holds verbatim. As is standard, the completeness of the graph suffices to show
finite algebra of measurable sets holds verbatim. As is standard, the completeness of the graph suffices to show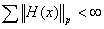 . That
. That 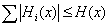 implies that it is absolutely summable, which is that,
implies that it is absolutely summable, which is that, 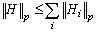 . It follows that
. It follows that 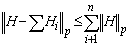 , a consequence of Banach space. We note in passing that if
, a consequence of Banach space. We note in passing that if 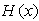 is not Hausdorff, an extreme point is not a supporting set.
is not Hausdorff, an extreme point is not a supporting set.
4. Distribution of Eigenvalues of the Jacobian Matrix
A very important issue in engineering application has always been the occurrence of a saddle node bifurcation , Hopf bifurcation or solution near such bifurcation points,[20]. Denoting A(x) as the Jacobian matrix of partial derivative of F(x) assuming that system 1.1 is of order n, the eigenvalues of A(x) is represented by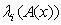 . Let
. Let 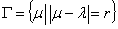 which does not contain eigenvalues of A other than
which does not contain eigenvalues of A other than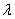 . Then
. Then 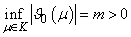 . The number of zeros
. The number of zeros 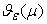 inside
inside 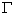 is given by argument principle [10]
is given by argument principle [10]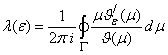 | (4.1) |
Thus 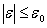 , the integral is analytic function of
, the integral is analytic function of 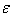 and of
and of 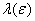 .In other words assuming
.In other words assuming 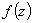 is analytic in the sense of [21] inside and on a closed contour
is analytic in the sense of [21] inside and on a closed contour 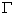 which encloses
which encloses 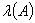 , then
, then 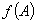 will be defined by the equation
will be defined by the equation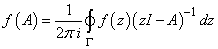 | (4.2) |
Supposing the eigenvalues are able to discriminate their goals such that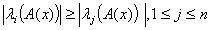 | (4.3) |
And assuming further one can find 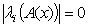 , then
, then 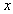 is called a saddle-node bifurcation point of the nonlinear system of equation 1.1. Furthermore, if A(x) has a pair of conjugate eigenvalues passing the imaginary axis while the other eigenvalues have negative real parts, then is called a Hopf bifurcation point.The solution to nonlinear system 1.1 is said to be stable if the eigenvalues of A(x) have negative real part.Using [17], the 2-norm,
is called a saddle-node bifurcation point of the nonlinear system of equation 1.1. Furthermore, if A(x) has a pair of conjugate eigenvalues passing the imaginary axis while the other eigenvalues have negative real parts, then is called a Hopf bifurcation point.The solution to nonlinear system 1.1 is said to be stable if the eigenvalues of A(x) have negative real part.Using [17], the 2-norm, 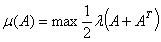 for unsymmetrical matrix
for unsymmetrical matrix 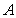 is the numerical abscissa
is the numerical abscissa 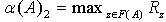 where in its application, the behaviour of
where in its application, the behaviour of 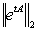 may be different in the initial, transient, and asymptotic phase. In other words, the asymptotic behaviour depends on
may be different in the initial, transient, and asymptotic phase. In other words, the asymptotic behaviour depends on 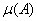 as
as 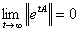 whenever
whenever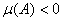 . In any case, the bound given by
. In any case, the bound given by 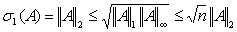 is the best possible.The cosine angle between two matrices
is the best possible.The cosine angle between two matrices 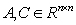 using Frobenius inner product is given by
using Frobenius inner product is given by 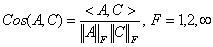 | (4.4) |
Where 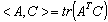 , [20] and
, [20] and 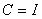 is often used in practice in which case
is often used in practice in which case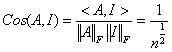 | (4.5) |
The relative condition numbers for the matrix sine and cosine in the sense of [22] satisfy 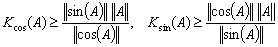 | (4.6) |
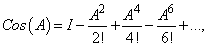
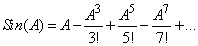 After all these, the estimation of eigenvalues of interval Jacobian matrices will be computed. Popular such methods for estimating bounds of eigenvalues have been the Gesrchgorin disks or Ovals of Cassini, [23]. Unfortunately the bounds these methods produce for the case of interval matrices had been known to be too wide for any meaningful uses. We proceed in the same spirit similar to [24] as well as [25] to provide realistic bounds for eigenvalues of interval matrices coming from the Jacobian of system 1.1.For general treatment of eigenvalues, consider unsymmetric matrices of order n where for clarity, we adopt the following notation:
After all these, the estimation of eigenvalues of interval Jacobian matrices will be computed. Popular such methods for estimating bounds of eigenvalues have been the Gesrchgorin disks or Ovals of Cassini, [23]. Unfortunately the bounds these methods produce for the case of interval matrices had been known to be too wide for any meaningful uses. We proceed in the same spirit similar to [24] as well as [25] to provide realistic bounds for eigenvalues of interval matrices coming from the Jacobian of system 1.1.For general treatment of eigenvalues, consider unsymmetric matrices of order n where for clarity, we adopt the following notation: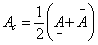 ,
, 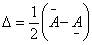 , and after verification of
, and after verification of 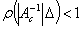 Rohn showed that a necessary and sufficient condition for
Rohn showed that a necessary and sufficient condition for 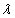 to be eigenvalue of interval matrix [A] is that
to be eigenvalue of interval matrix [A] is that 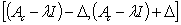 is singular. That is to say a number
is singular. That is to say a number 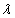 is an eigenvalue of
is an eigenvalue of 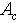 if the two conditions below can be verified
if the two conditions below can be verified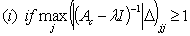 then
then 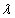 is a real eigenvalue of A
is a real eigenvalue of A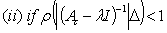 then
then  is not a real eigenvalue of A[22] proved that eigenvalues of symmetric interval matrix A lie in the interval
is not a real eigenvalue of A[22] proved that eigenvalues of symmetric interval matrix A lie in the interval 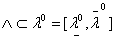 where
where 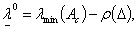
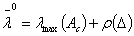 .The
.The 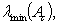
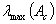 respectively denote minimal and maximal eigenvalue of
respectively denote minimal and maximal eigenvalue of 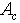 . Let us take note that a rectangular matrix
. Let us take note that a rectangular matrix 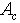 has full column rank if it possible to compute
has full column rank if it possible to compute 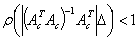 . For example the upper end point
. For example the upper end point  of the desired interval indicates how fast a population can grow or how fast a disease can spread in any experimental data analysis. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method has the drawback of still not being empty even when the set of eigenvalues is empty.
of the desired interval indicates how fast a population can grow or how fast a disease can spread in any experimental data analysis. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method has the drawback of still not being empty even when the set of eigenvalues is empty.
5. Numerical Examples
Problem 1.Consider a set of two-dimensional points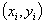 :
: Using quadratic polynomial fit for the data set and if we take notice of the resulting Vandermode matrix, and using MATLAB version 2007, the solution for equation 2.1 is obtained as
Using quadratic polynomial fit for the data set and if we take notice of the resulting Vandermode matrix, and using MATLAB version 2007, the solution for equation 2.1 is obtained as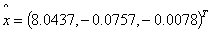 , with eigenvalues to the symmetric matrix
, with eigenvalues to the symmetric matrix 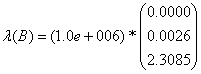 .Providing solution to the interval linear system a procedure earlier described in [15] applies. As a consequence, we omit repeating it here.We are concerned with providing estimates of the eigenvalues computed for interval matrix which was derived from the above statistical data set
.Providing solution to the interval linear system a procedure earlier described in [15] applies. As a consequence, we omit repeating it here.We are concerned with providing estimates of the eigenvalues computed for interval matrix which was derived from the above statistical data set And this was computed to be
And this was computed to be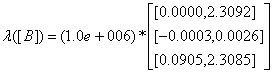 .Using Rohn’s method [24] we also obtained eigenvalues bound to be
.Using Rohn’s method [24] we also obtained eigenvalues bound to be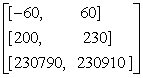 Using a 20% impurity as data noise we obtained bounds for eigenvalues of interval matrix as
Using a 20% impurity as data noise we obtained bounds for eigenvalues of interval matrix as  With condition number
With condition number 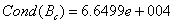 and it can be seen that matrix eigenvalues may be affected by level of impurities in the statistical data set.
and it can be seen that matrix eigenvalues may be affected by level of impurities in the statistical data set.
6. Conclusions
The paper studied graph completion operator for interval least squares problem. We discussed the statistical meaning of the matrix 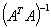 obtained from the statistical data entries of observation. It is shown that convergence of inverse operators for the resulting regularized Tikhonov parameter implies convergence in the tempered distribution of data noise wherein the earlier procedure described in [15] is applicable. Our emphasis was placed on estimating interval matrix which has great applications in the study of growth rate of a system which was applied on statistical least squares problem. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method [24] has the drawback of still not being empty even when the set of eigenvalues may be empty as demonstrated by numerical example. This may be found useful in both Scientific and Engineering designs.
obtained from the statistical data entries of observation. It is shown that convergence of inverse operators for the resulting regularized Tikhonov parameter implies convergence in the tempered distribution of data noise wherein the earlier procedure described in [15] is applicable. Our emphasis was placed on estimating interval matrix which has great applications in the study of growth rate of a system which was applied on statistical least squares problem. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method [24] has the drawback of still not being empty even when the set of eigenvalues may be empty as demonstrated by numerical example. This may be found useful in both Scientific and Engineering designs.
References
| [1] | Iyahen S.O (1998). The Closed Graph Theorem, Osaruwa Educational Publications, First Edition, Benin City. |
| [2] | Wikipedia (2014). Closed graph theorem. The free encyclopaedia, Mozila Fireworks. |
| [3] | Mane R (1987). Ergodic Theory and Differentiable Dynamicss, Springer-Verlag. |
| [4] | Oxtoby JC (1980). Measure and Category, Springer-Verlag. |
| [5] | Schodl P and Neumaier A (2010). Continuity notions for multivalued mappings with possibly disconnected images. Reliable Computing, pp 1-18. |
| [6] | Kelner JA (2006). Spectral partitioning, eigenvalue bounds, and circle packings for graphs of bounded genus, SIAM J. Comput Vol. 35 No 35, PP. 882-902. |
| [7] | Martinez JM (1994). Algorithms for solving nonlinear systems of equations, Continuous optimization: the state or art (In edt. Spedicato E), Kluwer, 81-108. |
| [8] | Neumaier A (2000). Introduction to Numerical analysis, Cambridge University Press, Cambridge. |
| [9] | Ortega JM and Rheinboldt WC (2000). Iterative solution of nonlinear equations in several variables, SIAM, Philadelphia. |
| [10] | Stoer J and Bulirsch R (1983). Introduction to Numerical Analysis, Springer-Verlag, New York. |
| [11] | Neumaier A (2004). Complete search in continuous global optimization and constraint satisfaction. A Chapter for Acta Numerical 2004 (A. Iserles, ed.), Cambridge University Press. |
| [12] | Bini D and Pan V (1994). Polynomial and matrix Computations Vol. 1: Fundamental algorithms, Birkhauser, Boston. |
| [13] | Stefan W. (2008). Total Variation regularization for linear Ill-posed inverse problems: Extensions and application, PhD thesis, Graduate College, Arizona State University , USA. |
| [14] | Ferson S, Kreinovich V, Hajagos J, Oberkamp W and Ginzburg L (2007). Experimental uncertainty estimation and statistics for Data having interval uncertainty. SAND 2007-0939 Unlimited release. Available online at http//:www.amas.com/inststats.pdf |
| [15] | Uwamusi SE (2014). Regularization of Non-smooth function whose Jacobian is nearly singular or singular, America International Journal of Contemporary Scientific Research-180, ISSN 2349-4425. Available in www.americanij.com |
| [16] | El-Ghaoui L and Lebret H (1977). Robust solutions to least-squares problems with uncertain data, SIAM J. Matrix Anal. Appl Vol 18(4) pp 1035-1064. |
| [17] | Bjorck A, (2009). Numerical methods in Scientific Computing Vol. 2, SIAM, Philadephia. |
| [18] | Hargreaves G (2006). Computing the condition number of Tridiagonal and diagonal-plus semiseprable matrices in linear time, SIAM J. Matrix Anal. Appl, 27(30, PP. 801-820. |
| [19] | Borwein JM and Zhuang DM (1988) Variable necessary and sufficient conditions for openness and regularity of set-valued and Single-valued maps, Journal of Mathematical analysis and applications 134, 441-459. |
| [20] | Kelly CT, Qi L , Tong X and Yin H (2011). Finding a stable solution of a system of Nonlinear equations arising from Dynamic systems, Journal of Industrial and Management Optimization, 7(2), 297. |
| [21] | Tarazaga P (1989). More estimates for eigenvalues and singular values, TR 89-6. |
| [22] | Higham NJ (2009). Functions of Matrices: Theory and Computation, SIAM Philadelphia. |
| [23] | Varga RS (2000). Matrix iterative analysis, Springer Computational Mathematics, Second Edition, New York. |
| [24] | Rohn J (2005). A Handbook of results on interval analysis, Czech Academy of Sciences, Prague, Czech Republic, European Union. |
| [25] | Hadlik M, Daney D and Tsigaridas EP (2008). Bounds on eigenvaues and singular values of interval matrices, INRIA Institut National Recherche en infomatique et en automatique . |
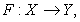 we define the graph
we define the graph 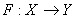 , as the map
, as the map 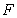 to be the Cartessian product
to be the Cartessian product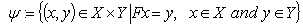 .There is a metric topology for which is defined
.There is a metric topology for which is defined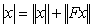 . When
. When 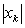 is Cauchy, for
is Cauchy, for 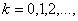 it follows that
it follows that 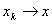 in
in 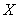 as
as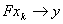 . In other words, for a closed graph F, it holds that
. In other words, for a closed graph F, it holds that 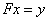 forcing
forcing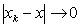 implying the graph of
implying the graph of 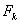 is enclosed by the convex hull of control points. In a nutshell, a graph
is enclosed by the convex hull of control points. In a nutshell, a graph 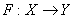 is continuous at the point
is continuous at the point 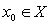 if it pulls open sets back to open sets and carries open sets over to open sets.Fundamental to this discussion are the basic principles of advanced topology. Good reference texts may be [1], [3] and [4]. Following [1], a linear map F from a linear topological space X to a linear topological space Y will be called bounded if it maps bounded sets to bounded sets. A map which is a linear topological space X to a linear topological space Y will be called sequentially continuous if for every sequence
if it pulls open sets back to open sets and carries open sets over to open sets.Fundamental to this discussion are the basic principles of advanced topology. Good reference texts may be [1], [3] and [4]. Following [1], a linear map F from a linear topological space X to a linear topological space Y will be called bounded if it maps bounded sets to bounded sets. A map which is a linear topological space X to a linear topological space Y will be called sequentially continuous if for every sequence 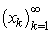 converging to some point x of E has a bounded envelope and such a sequentially continuous map is ultrabarrelled [1]. A function F is called approxable in the sense of [5] if for a multi valued mapping
converging to some point x of E has a bounded envelope and such a sequentially continuous map is ultrabarrelled [1]. A function F is called approxable in the sense of [5] if for a multi valued mapping 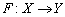 for every
for every 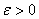 there is continuous single valued mapping
there is continuous single valued mapping 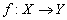 with graph
with graph 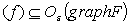 . A function
. A function 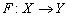 is said to be upper semi-continuous at
is said to be upper semi-continuous at 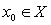 if for any neighbourhood
if for any neighbourhood 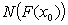 of
of 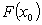 there exists a neighbourhood
there exists a neighbourhood 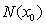 of
of 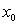 such that
such that 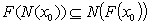 . A similar definition goes for a lower semi continuous function.By reasons due to recurrence and category theorem, the map
. A similar definition goes for a lower semi continuous function.By reasons due to recurrence and category theorem, the map 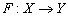 has a measure preserving homeomorphism and hence its set of recurrent point is residual and of full measure. In other words it can be said that such a map has a generic measure preserving homeomorphism whose square has a dense orbit. In some cases one often comes across some functions with distortions at some points which necessitate the following definition.Definition 1.1, [6]. Let
has a measure preserving homeomorphism and hence its set of recurrent point is residual and of full measure. In other words it can be said that such a map has a generic measure preserving homeomorphism whose square has a dense orbit. In some cases one often comes across some functions with distortions at some points which necessitate the following definition.Definition 1.1, [6]. Let 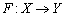 be a map between two locally Euclidean metric spaces. The quantity
be a map between two locally Euclidean metric spaces. The quantity 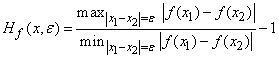 , is called the radius
, is called the radius 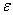 distortion of
distortion of 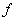 at x.As a consequence following, we introduce the nonlinear system of equation
at x.As a consequence following, we introduce the nonlinear system of equation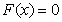
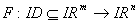 , m>n,
, m>n, 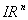 is an interval vector. It is supposed that the function F has at least
is an interval vector. It is supposed that the function F has at least 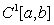 where
where 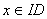 . Therefore, in a Frechet space E, every continuous linear map from a Frechet space E into F has a closed range and such a map is finite dimensional. Applications of nonlinear systems for example are well documented in the work of [7] which includes the following: Aircraft stability problems, Inverse Elastic rod problems, Equations of radiative transfer, Elliptic boundary value problems, Power flow problems, Distribution of water on a pipeline, Discretization of evolution problems using implicit schemes, Chemical plant equilibrium problems and, Nonlinear programming problems. We often adopt the concept of divided difference from a univariate function which is extended over to multivariate vector valued function by defining slope as
. Therefore, in a Frechet space E, every continuous linear map from a Frechet space E into F has a closed range and such a map is finite dimensional. Applications of nonlinear systems for example are well documented in the work of [7] which includes the following: Aircraft stability problems, Inverse Elastic rod problems, Equations of radiative transfer, Elliptic boundary value problems, Power flow problems, Distribution of water on a pipeline, Discretization of evolution problems using implicit schemes, Chemical plant equilibrium problems and, Nonlinear programming problems. We often adopt the concept of divided difference from a univariate function which is extended over to multivariate vector valued function by defining slope as 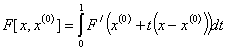 , provided that F is differentiable on the line
, provided that F is differentiable on the line 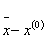 .Motivated by the above details, we state the following:Lemma 1.1, [8]. Let
.Motivated by the above details, we state the following:Lemma 1.1, [8]. Let 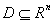 be convex and let
be convex and let 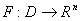 be continuously differentiable in D.(i) If
be continuously differentiable in D.(i) If 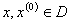 then
then 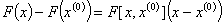 (This is a strong form of Mean-value theorem);(ii) if
(This is a strong form of Mean-value theorem);(ii) if 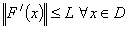 then
then 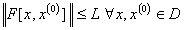 and
and 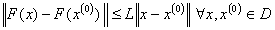 (This is a weak form of Mean-value theorem);(iii) if
(This is a weak form of Mean-value theorem);(iii) if 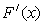 is Lipschitz continuous in D, that is the relation
is Lipschitz continuous in D, that is the relation 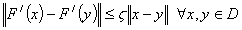 holds for some
holds for some 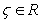 , then
, then 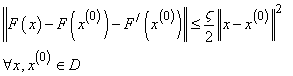 (This is truncated Taylor expansion with remainder term).It is a result to follow up to the discussion that we have the following theorems.Theorem 1.1, [9]. Suppose
(This is truncated Taylor expansion with remainder term).It is a result to follow up to the discussion that we have the following theorems.Theorem 1.1, [9]. Suppose 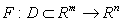 has an F-derivative at each point of an open neighbourhood of
has an F-derivative at each point of an open neighbourhood of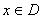 . Then,
. Then, 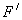 is strong at x if and only if
is strong at x if and only if 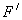 is continuous at
is continuous at 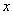 .Because system 1.1 is over determined, we often transform to a linear system by the process of 2-norm assuming that the Jacobian matrix
.Because system 1.1 is over determined, we often transform to a linear system by the process of 2-norm assuming that the Jacobian matrix 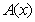 which is rectangular exists in the form
which is rectangular exists in the form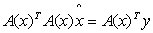
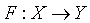 is closed in
is closed in 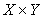 with respect to its product topology.Of paramount interest to us is a mapping that is balanced and absorbent whose inductive limit is ultra barrelled for which contraction mapping of Newton-Mysovskii theorem follows: Theorem 1.2, [9]. Supposing that
with respect to its product topology.Of paramount interest to us is a mapping that is balanced and absorbent whose inductive limit is ultra barrelled for which contraction mapping of Newton-Mysovskii theorem follows: Theorem 1.2, [9]. Supposing that 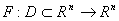 is F-differentiable on a convex set
is F-differentiable on a convex set 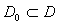 and that for each
and that for each 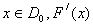 is non-singular and satisfies
is non-singular and satisfies 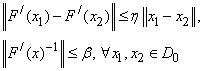 . Assuming further that
. Assuming further that 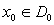 such that
such that 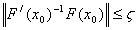 ;
; 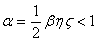 and
and 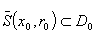 for which
for which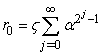 . Then the iterated contraction of Newton operator is in the form:
. Then the iterated contraction of Newton operator is in the form: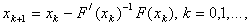
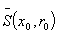 and converges to a solution
and converges to a solution 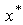 of
of 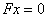 .Moreover,
.Moreover,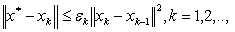 where
where 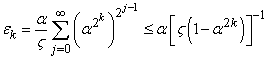 .We expect the weak pre-image
.We expect the weak pre-image 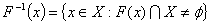 and the strong pre-image
and the strong pre-image 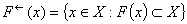 coincide simultaneously such that the orbit of F is a sequence
coincide simultaneously such that the orbit of F is a sequence 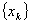 for which
for which 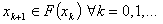
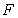 be coercive and a local homeomorphism of
be coercive and a local homeomorphism of 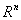 to itself, every zero of
to itself, every zero of 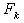 is in the intersection of convex hull with the hyper plane
is in the intersection of convex hull with the hyper plane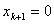 .As a result of equation 1.4 the norm reducing property of Newton operator for system 1.1 is given by
.As a result of equation 1.4 the norm reducing property of Newton operator for system 1.1 is given by 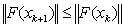 for k=0,1,.., .The quantity
for k=0,1,.., .The quantity 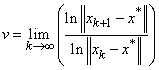 will be called the order of convergence for
will be called the order of convergence for 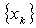 assuming the limit exists which is again equal to the R-Order of convergence of [9].The rest part in the paper is arranged as follows: Section 2 discusses what is meant by the statistical meaning of the matrix
assuming the limit exists which is again equal to the R-Order of convergence of [9].The rest part in the paper is arranged as follows: Section 2 discusses what is meant by the statistical meaning of the matrix 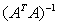 . Section 3 describes completeness of graph in Banach space topology. Procedure for estimating eigenvalues of interval Jacobian matrix formed the basis of discussion in chapter 4. Section 5 in the paper gives numerical illustration of what has been discussed in previous sections.
. Section 3 describes completeness of graph in Banach space topology. Procedure for estimating eigenvalues of interval Jacobian matrix formed the basis of discussion in chapter 4. Section 5 in the paper gives numerical illustration of what has been discussed in previous sections.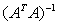 and Its Applications
and Its Applications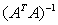 . We note that the components
. We note that the components 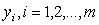 are independent, normally distributed random variable with mean
are independent, normally distributed random variable with mean 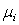 and all having the same variance
and all having the same variance 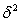 which we describe in the form:
which we describe in the form: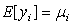 ,
, 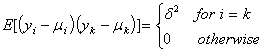 Therefore setting
Therefore setting 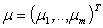 there holds that
there holds that 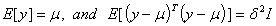 The covariance matrix of the random vector y is given by
The covariance matrix of the random vector y is given by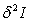 . The first moments are
. The first moments are 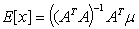 and
and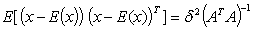 . For a rectangular matrix A for which
. For a rectangular matrix A for which 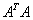 is non singular Nuemaier [11] using
is non singular Nuemaier [11] using 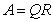 decomposition proved that
decomposition proved that 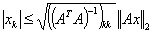 for all x.Following [12], it was proved that over any field,
for all x.Following [12], it was proved that over any field, 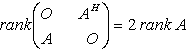 and that
and that 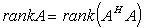 holds over any field of characteristic 0. This means computing least squares solution or bounding the errors of computations are not defined over an arbitrary field. It thus holds that
holds over any field of characteristic 0. This means computing least squares solution or bounding the errors of computations are not defined over an arbitrary field. It thus holds that 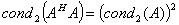 and that
and that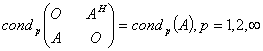 .We shall be interested in the least squares problem where the coefficient matrix and right hand vector assume some kind of noise often known as white noise. This situation leads to what is called Total Least Squares Problem (TLS) whereby, tempered distribution to the coefficient matrix A is
.We shall be interested in the least squares problem where the coefficient matrix and right hand vector assume some kind of noise often known as white noise. This situation leads to what is called Total Least Squares Problem (TLS) whereby, tempered distribution to the coefficient matrix A is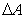 , and to the vector y by
, and to the vector y by 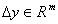 respectively for which holds
respectively for which holds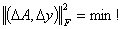
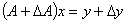
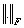 is the usual Frobenius norm which coincides with
is the usual Frobenius norm which coincides with 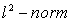 in the classical Banach space. In its simplest form, the linear inverse problem [13], [14] to which the least squares problem belongs was described in the form:
in the classical Banach space. In its simplest form, the linear inverse problem [13], [14] to which the least squares problem belongs was described in the form: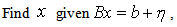
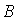 represents
represents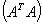 ,
, 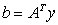 , and
, and 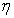 is the realization of random noise. Thus when B is invertible the linear system 2.3 is said to be well posed whereas it is ill-posed when B is not invertible.As a result the minimum
is the realization of random noise. Thus when B is invertible the linear system 2.3 is said to be well posed whereas it is ill-posed when B is not invertible.As a result the minimum 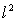 -norm of the residual is given by
-norm of the residual is given by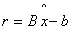
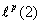 is the norm on
is the norm on 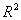 with unit ball defined by
with unit ball defined by 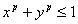 ..By substituting (2.4) into (1.1) we have that
..By substituting (2.4) into (1.1) we have that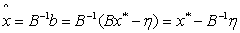
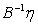 dominates in the ill-posed problem when the uncertainty is high thereby making
dominates in the ill-posed problem when the uncertainty is high thereby making  practically useless in most cases of applications. This means that the induced map
practically useless in most cases of applications. This means that the induced map 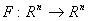 is open, nearly continuous, and nearly open if and only if
is open, nearly continuous, and nearly open if and only if 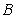 has the same ill-posed property, [1]. Therefore via interval arithmetic this problem has been addressed [15].We expect that both
has the same ill-posed property, [1]. Therefore via interval arithmetic this problem has been addressed [15].We expect that both 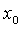 and
and 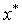 be closed in the
be closed in the 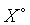 topology [1] so that,
topology [1] so that, 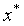 convergence implies convergence in the tempered distribution for which any neighbourhood
convergence implies convergence in the tempered distribution for which any neighbourhood 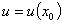 in the metric space
in the metric space 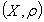 holds for
holds for 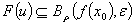 satisfying system 1.1.As pointed by some schools of thought, one drawback of Tikhonov regularization is that it tends to produce a solution that is often excessively smooth in image processing for which this method results in loss of sharpness. Nevertheless, the classical Tikhonov regularization method for minimizing
satisfying system 1.1.As pointed by some schools of thought, one drawback of Tikhonov regularization is that it tends to produce a solution that is often excessively smooth in image processing for which this method results in loss of sharpness. Nevertheless, the classical Tikhonov regularization method for minimizing 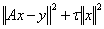 has the solution as
has the solution as 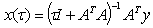 in the sense of [16]. The equation that determines
in the sense of [16]. The equation that determines 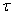 in the restructured least squares sense was given by
in the restructured least squares sense was given by 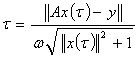
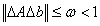 is well defined.Thus when
is well defined.Thus when 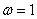 the optimal solution is given by
the optimal solution is given by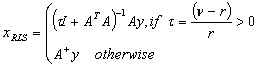 Where
Where 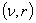 are the unique optimal point to the problem minimize
are the unique optimal point to the problem minimize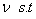
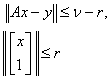 Note that
Note that 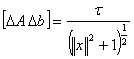 and
and 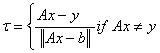 .Since
.Since 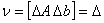 and
and  is rank one, it holds that
is rank one, it holds that 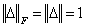 . This forces
. This forces 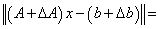
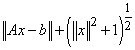 .Equation 2.6 is used when there is no perturbation in y. In case of total least squares the solution to the perturbed least squares equation 2.1 is given by the
.Equation 2.6 is used when there is no perturbation in y. In case of total least squares the solution to the perturbed least squares equation 2.1 is given by the 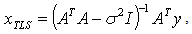
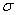 is the smallest singular value of
is the smallest singular value of 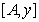 , ([ 17], e.g.,). In most applications of interest we often perturb the matrix B such that perturbation
, ([ 17], e.g.,). In most applications of interest we often perturb the matrix B such that perturbation 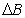 satisfies the condition that
satisfies the condition that 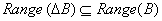 and
and 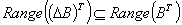
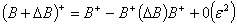
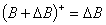 , and
, and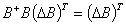 . The matrix
. The matrix 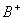 is the Pseudo-Penrose inverse of
is the Pseudo-Penrose inverse of 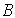 .As a result of equations 2.8 and 2.9 and in view of equation 2.7, it can be deduced that
.As a result of equations 2.8 and 2.9 and in view of equation 2.7, it can be deduced that 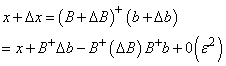
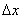 as well as
as well as 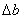 is obtained in the form
is obtained in the form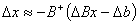
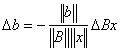
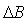 , from well known result [18] there holds the estimate
, from well known result [18] there holds the estimate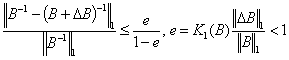
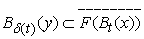 , an indication that F is open around
, an indication that F is open around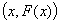 and
and 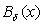 is the open
is the open 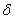 -neighbourhood of x in
-neighbourhood of x in 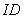 . That is,
. That is,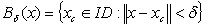
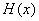 satisfying the inclusion
satisfying the inclusion 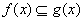 which is Dedekind order complete
which is Dedekind order complete  with respect to point wise defined partial ordering. As it were, we also assume that
with respect to point wise defined partial ordering. As it were, we also assume that 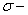 finite algebra of measurable sets holds verbatim. As is standard, the completeness of the graph suffices to show
finite algebra of measurable sets holds verbatim. As is standard, the completeness of the graph suffices to show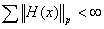 . That
. That 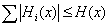 implies that it is absolutely summable, which is that,
implies that it is absolutely summable, which is that, 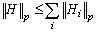 . It follows that
. It follows that 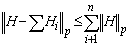 , a consequence of Banach space. We note in passing that if
, a consequence of Banach space. We note in passing that if 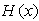 is not Hausdorff, an extreme point is not a supporting set.
is not Hausdorff, an extreme point is not a supporting set.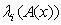 . Let
. Let 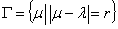 which does not contain eigenvalues of A other than
which does not contain eigenvalues of A other than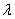 . Then
. Then 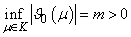 . The number of zeros
. The number of zeros 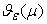 inside
inside 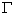 is given by argument principle [10]
is given by argument principle [10]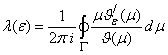
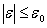 , the integral is analytic function of
, the integral is analytic function of 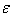 and of
and of 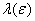 .In other words assuming
.In other words assuming 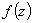 is analytic in the sense of [21] inside and on a closed contour
is analytic in the sense of [21] inside and on a closed contour 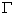 which encloses
which encloses 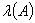 , then
, then 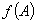 will be defined by the equation
will be defined by the equation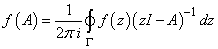
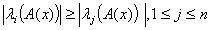
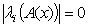 , then
, then  is called a saddle-node bifurcation point of the nonlinear system of equation 1.1. Furthermore, if A(x) has a pair of conjugate eigenvalues passing the imaginary axis while the other eigenvalues have negative real parts, then is called a Hopf bifurcation point.The solution to nonlinear system 1.1 is said to be stable if the eigenvalues of A(x) have negative real part.Using [17], the 2-norm,
is called a saddle-node bifurcation point of the nonlinear system of equation 1.1. Furthermore, if A(x) has a pair of conjugate eigenvalues passing the imaginary axis while the other eigenvalues have negative real parts, then is called a Hopf bifurcation point.The solution to nonlinear system 1.1 is said to be stable if the eigenvalues of A(x) have negative real part.Using [17], the 2-norm, 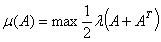 for unsymmetrical matrix
for unsymmetrical matrix 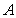 is the numerical abscissa
is the numerical abscissa 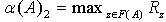 where in its application, the behaviour of
where in its application, the behaviour of 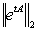 may be different in the initial, transient, and asymptotic phase. In other words, the asymptotic behaviour depends on
may be different in the initial, transient, and asymptotic phase. In other words, the asymptotic behaviour depends on 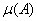 as
as 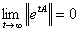 whenever
whenever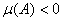 . In any case, the bound given by
. In any case, the bound given by 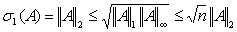 is the best possible.The cosine angle between two matrices
is the best possible.The cosine angle between two matrices 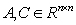 using Frobenius inner product is given by
using Frobenius inner product is given by 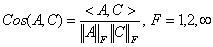
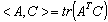 , [20] and
, [20] and 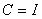 is often used in practice in which case
is often used in practice in which case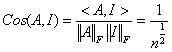
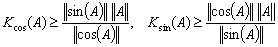
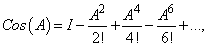
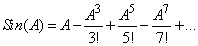 After all these, the estimation of eigenvalues of interval Jacobian matrices will be computed. Popular such methods for estimating bounds of eigenvalues have been the Gesrchgorin disks or Ovals of Cassini, [23]. Unfortunately the bounds these methods produce for the case of interval matrices had been known to be too wide for any meaningful uses. We proceed in the same spirit similar to [24] as well as [25] to provide realistic bounds for eigenvalues of interval matrices coming from the Jacobian of system 1.1.For general treatment of eigenvalues, consider unsymmetric matrices of order n where for clarity, we adopt the following notation:
After all these, the estimation of eigenvalues of interval Jacobian matrices will be computed. Popular such methods for estimating bounds of eigenvalues have been the Gesrchgorin disks or Ovals of Cassini, [23]. Unfortunately the bounds these methods produce for the case of interval matrices had been known to be too wide for any meaningful uses. We proceed in the same spirit similar to [24] as well as [25] to provide realistic bounds for eigenvalues of interval matrices coming from the Jacobian of system 1.1.For general treatment of eigenvalues, consider unsymmetric matrices of order n where for clarity, we adopt the following notation: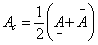 ,
, 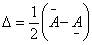 , and after verification of
, and after verification of 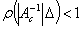 Rohn showed that a necessary and sufficient condition for
Rohn showed that a necessary and sufficient condition for 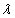 to be eigenvalue of interval matrix [A] is that
to be eigenvalue of interval matrix [A] is that 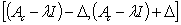 is singular. That is to say a number
is singular. That is to say a number 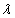 is an eigenvalue of
is an eigenvalue of 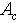 if the two conditions below can be verified
if the two conditions below can be verified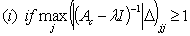 then
then 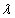 is a real eigenvalue of A
is a real eigenvalue of A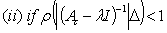 then
then  is not a real eigenvalue of A[22] proved that eigenvalues of symmetric interval matrix A lie in the interval
is not a real eigenvalue of A[22] proved that eigenvalues of symmetric interval matrix A lie in the interval 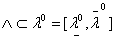 where
where 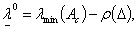
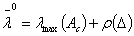 .The
.The 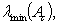
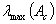 respectively denote minimal and maximal eigenvalue of
respectively denote minimal and maximal eigenvalue of 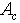 . Let us take note that a rectangular matrix
. Let us take note that a rectangular matrix 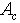 has full column rank if it possible to compute
has full column rank if it possible to compute 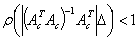 . For example the upper end point
. For example the upper end point 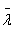 of the desired interval indicates how fast a population can grow or how fast a disease can spread in any experimental data analysis. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method has the drawback of still not being empty even when the set of eigenvalues is empty.
of the desired interval indicates how fast a population can grow or how fast a disease can spread in any experimental data analysis. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method has the drawback of still not being empty even when the set of eigenvalues is empty.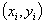 :
: Using quadratic polynomial fit for the data set and if we take notice of the resulting Vandermode matrix, and using MATLAB version 2007, the solution for equation 2.1 is obtained as
Using quadratic polynomial fit for the data set and if we take notice of the resulting Vandermode matrix, and using MATLAB version 2007, the solution for equation 2.1 is obtained as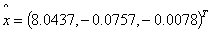 , with eigenvalues to the symmetric matrix
, with eigenvalues to the symmetric matrix 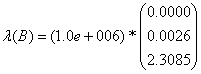 .Providing solution to the interval linear system a procedure earlier described in [15] applies. As a consequence, we omit repeating it here.We are concerned with providing estimates of the eigenvalues computed for interval matrix which was derived from the above statistical data set
.Providing solution to the interval linear system a procedure earlier described in [15] applies. As a consequence, we omit repeating it here.We are concerned with providing estimates of the eigenvalues computed for interval matrix which was derived from the above statistical data set And this was computed to be
And this was computed to be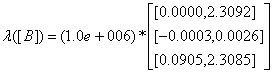 .Using Rohn’s method [24] we also obtained eigenvalues bound to be
.Using Rohn’s method [24] we also obtained eigenvalues bound to be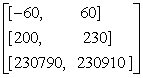 Using a 20% impurity as data noise we obtained bounds for eigenvalues of interval matrix as
Using a 20% impurity as data noise we obtained bounds for eigenvalues of interval matrix as  With condition number
With condition number 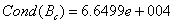 and it can be seen that matrix eigenvalues may be affected by level of impurities in the statistical data set.
and it can be seen that matrix eigenvalues may be affected by level of impurities in the statistical data set.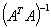 obtained from the statistical data entries of observation. It is shown that convergence of inverse operators for the resulting regularized Tikhonov parameter implies convergence in the tempered distribution of data noise wherein the earlier procedure described in [15] is applicable. Our emphasis was placed on estimating interval matrix which has great applications in the study of growth rate of a system which was applied on statistical least squares problem. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method [24] has the drawback of still not being empty even when the set of eigenvalues may be empty as demonstrated by numerical example. This may be found useful in both Scientific and Engineering designs.
obtained from the statistical data entries of observation. It is shown that convergence of inverse operators for the resulting regularized Tikhonov parameter implies convergence in the tempered distribution of data noise wherein the earlier procedure described in [15] is applicable. Our emphasis was placed on estimating interval matrix which has great applications in the study of growth rate of a system which was applied on statistical least squares problem. As pointed out by [24] the estimated eigenvalue bound provided by Rohn’s method [24] has the drawback of still not being empty even when the set of eigenvalues may be empty as demonstrated by numerical example. This may be found useful in both Scientific and Engineering designs. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML