1. Introduction

Announced in 1954, PP Kufarev [1] method of, combining method of parametric representations and method of internal variations in the theory conformal maps, was developed and is widely used in a large number of works executed in Tomsk school of the theory of functions of a complex variable, PP Kufarev, IA Aleksandrov, AI Alexandrov, VA Andeanvian Jews, MA Arendarchuk, VV Baranova, LM Behr, NV Genin VJ Gutlyanskim, VI Kahn, TV Kasatkina, G.Ya.Keselmanom, LS Kopaneva, SA Kopaneva, MR Kuvayev, VP Mandikom, YA Martynov, VA Nazarova, MN Nikulshin, RS Polomoshnova, VI Popov, GA Popova, AE Prochoral, MI Redkovym, GD Sadritdinova, VV Sobolev, AS Sorokinnym, LV Sporysheva, PI Sizhuk, AN Syrkashevym, AE Thales, BG colorkov, VV Chernikov, VV Schepetevym, Abunawas K.A and others.

Extremal problems geometric function of a complex variable are closely related with the main objectives of both the the theory and it’s the many applications. In an article devoted to further and to the method Kufarev application to the case of conformal mapping the upper half-plane into polygonal region in the presence of the boundary normalization. The article provides Loewner differential equation for the half-plane with a cut along the a Jordan curve, provided that the points 0, 1, and 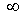remain fixed.

PP Kufarev took the original formula GM Goluzina [2] and artfully applied it to the mapping of the plane with a cut is shortened, ie to levnerovskim areas.

Application received Kufarev formula for extreme tasks will allow to characterize the extreme display for a large number of functional is not one, as was done previously, and two complementary equations and in many cases bring the study of extreme tasks to complete solutions.

In [3] the same method yielded the variational formula Goluzina. It is used in this paper with a brief repetition of its output.

2. Explanation of Methods

Let the function 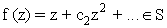displays the circle 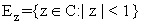in the area 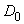, derived from 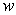– plane carrying Jordan piecewise smooth cut 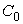, starting at the end point of the plane , not passing through the point 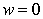and ending at infinity. Let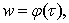 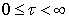, – parametric equation of the curve 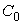. Region 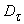is obtained by adding to 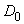arcs 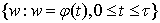and displayed in a final function 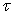, , 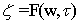, , 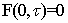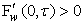on the circle 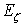. This display only.

Changing properly parameterization of the curve 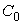, You can achieve that .

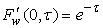Let us assume the selected parameterization 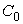immediately under this condition.

form the function 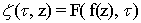, It displays circle 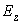to circle 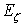with cut along Jordan piecewise smooth curve, which does not pass through zero.

Obvious

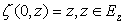Let 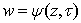- function, the inverse of 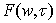, for fixed 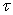. Easy to see that , , .

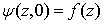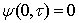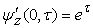Exists a piecewise smooth function 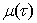, , 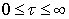, 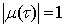it is called the control, such that 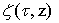is a solution of the Löwner [4]

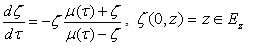(1)

And

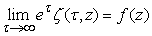Moreover, 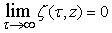, for any 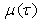in equation (1).

Let the

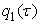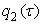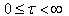, , – real continuous functions

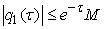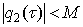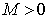, , . the control function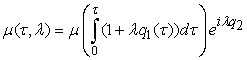

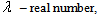
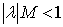, corresponds to a solution, 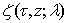the Löwner equation

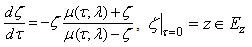(2)

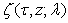Function is univalent conformal displays the 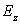in the unit circle and

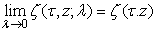uniformly inside 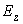, because 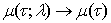, when

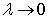Replace in equation (2) variable 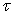to 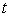according to the formula 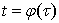, when

.

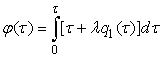Since the further we will be interested only in the linear part of the expansion with respect to 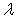, , 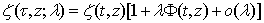it suffices to restrict when changing 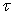into 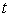the equations for the 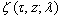in the form

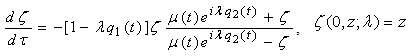(3)

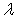As a result, a simple operation using the Taylor series expansion in powers for find 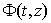, 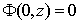equation

.

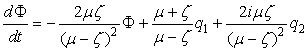Its solution is given by

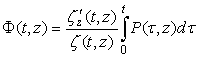Where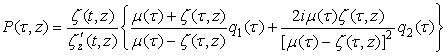

So the formula,

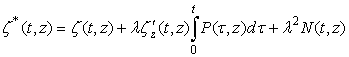(4)

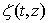indicates how to change solution Löwner equation when changing in him control function 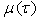for 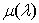. Function 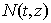is limited uniformly in t in .

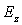The further constructions associated with a specific selection 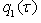and .

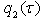Let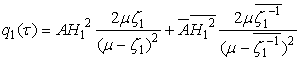

,

,

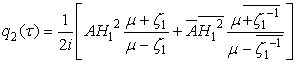where 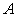– constant, 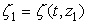, , 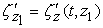, 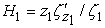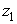– point of .

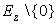Then the

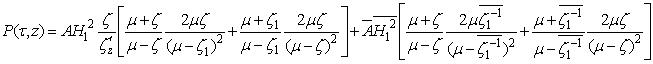For two different solutions 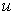, 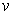Löwner equation, is easy to verify, formula holds,

,

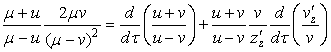allowing to submit 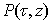in the form

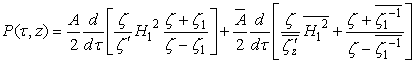and thus, write the formula (4) as

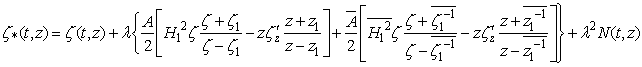Multiply both sides the resulting formula for 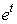and take the limit 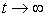. A result we have

,

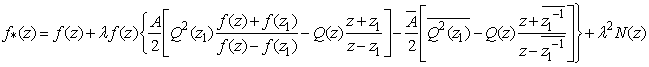Where

, .

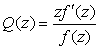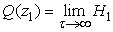The function 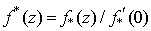, : , 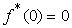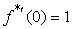Normalized by the conditions, and represents a variational formula under consideration subclass of 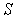. It easy to applies to class 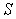also and is known for variational formula Goluzina in class .

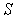Using the variational the formula Goluzina

,

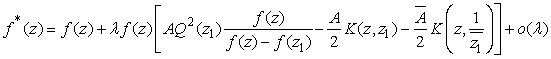Where

,

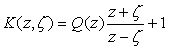represent display 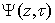circle 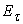to some area close 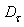to the 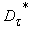in the form

,

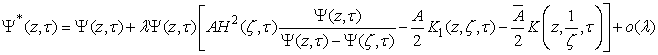Where

, ,

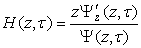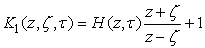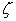– fixed point in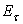

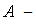constant

Function of 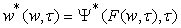, , 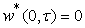maps the domai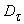n on 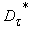; at the same function 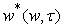displays the 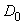on the area 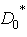, close to the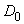. Decomposition 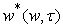in powers of 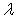is given by

,

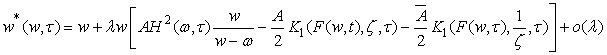Where .

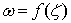Replacing in this formula 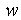to 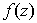. get the function 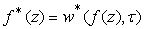, univalent conformal mapping the disk 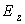onto the domain .

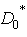It is easy to find

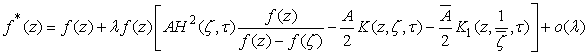(5)

There

.

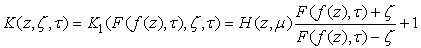
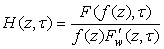Equation (5) given to Kufarev.

3. Conclusions

In it participates function 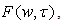which is associated function for 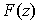satisfies the equation Löwner

, .

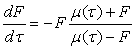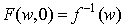This fact allows us in many of variational problems to get two equations for the function, attached to extremal function relatively large number of functional tasks encountered in geometric function theory of complex variable.

In this article we give a conclusion variational formula Kufarev other way, staying strictly within the framework of the method parametric representations.

I hope that the article will be useful for specialists in complex analysis, and for mathematicians working in other areas and using methods of the modern theory of functions.