A. K. Olapade1, O. A. Adelodun2
1Department of Mathematics, Obafemi Awolowo University, Ile-Ife. Nigeria
2Institute of Education, Obafemi Awolowo University, Ile-Ife. Nigeria
Correspondence to: A. K. Olapade, Department of Mathematics, Obafemi Awolowo University, Ile-Ife. Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we obtain the distribution functions of the range and the quasi-range of the random variables arising from the type II generalized half logistic distribution.
Keywords:
Type II Generalized Half Logistic Distribution, Order Statistics, Range, Quasi-range
Cite this paper: A. K. Olapade, O. A. Adelodun, On the Distribution Functions of the Range and Quasi-Range for the Type II Generalized Half Logistic Distribution, American Journal of Mathematics and Statistics, Vol. 4 No. 6, 2014, pp. 241-247. doi: 10.5923/j.ajms.20140406.01.
1. Introduction
The probability density function of a continuous random variable X that follows an half logistic distribution is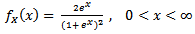 | (1.1) |
while its cumulative distribution function is 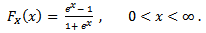 | (1.2) |
The half logistic distribution had been studied by many authors. Balakrishnan (1985) studied ordered statistics of the half logistic distribution. Balakrishnan and Puthenpura (1986) obtained best linear unbiased estimator of location and scale parameters of the distribution through linear functions of order statistics while Balakrishnan and Wong (1991) obtained approximate maximum likelihood estimates for the location and scale parameters of the distribution with Type II Right-Censoring. Olapade (2003) stated and proved some theorems that characterized the half logistic distribution. Olapade (2009) obtained a generalized form of the distribution with probability density function (pdf)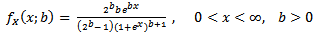 | (1.3) |
and its corresponding cumulative distribution function (cdf)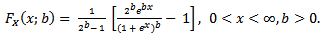 | (1.4) |
The pdf in equation (1.3) is called type II generalized half logistic distribution while the cdf is as in equation (1.4). The moment, median, mode and the 100p-percentile point including some theorems that characterize the type II generalized half logistic distribution were presented in Olapade (2009). In this paper, we want to obtain the distributions of the range and quasi-range of a sample from the type II generalized half logistic distribution as was done for extended type I generalized logistic distribution in Olapade (2010).
2. Distribution of the Range
Given a set of random variables 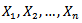 of size n coming from the type II generalized half logistic distribution and let
of size n coming from the type II generalized half logistic distribution and let 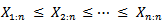 be the corresponding order statistics. Let
be the corresponding order statistics. Let 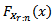 and
and 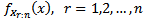 be the cdf and pdf of the rth order statistics
be the cdf and pdf of the rth order statistics 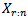 respectively. David (1970) obtained the pdf of
respectively. David (1970) obtained the pdf of 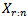 as
as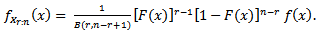 | (2.0) |
Let us define the sample range 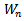 by
by 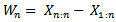 The cdf of
The cdf of 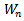 can be written as shown in Gupta and Shah (1965)
can be written as shown in Gupta and Shah (1965)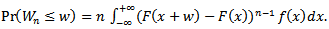 | (2.1) |
By expanding 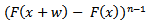 , we have
, we have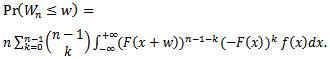 | (2.2) |
Substituting (1.3) and (1.4) in (2.2) we have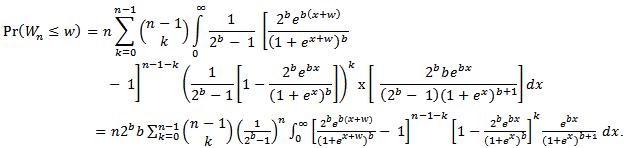 Since
Since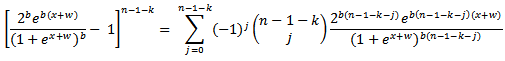 and
and 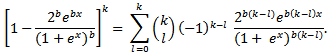 Therefore,
Therefore,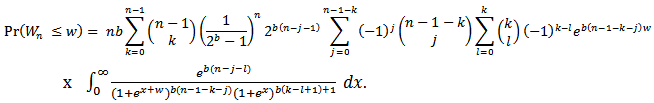 | (2.3) |
Now, we consider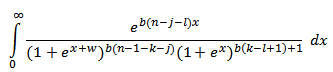 with the following transformations. Let
with the following transformations. Let 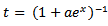 , where
, where 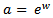 , then
, then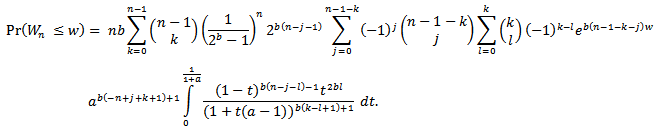 Let
Let 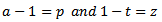 then with the intervals:
then with the intervals: 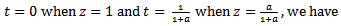
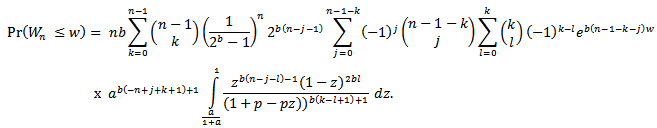 Let
Let 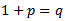 and
and 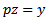 , then we have
, then we have 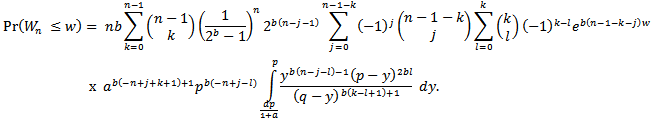
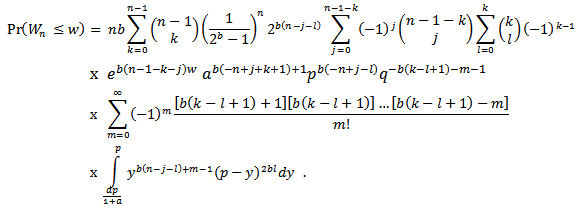 Since
Since 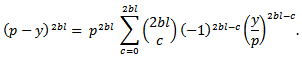 We have
We have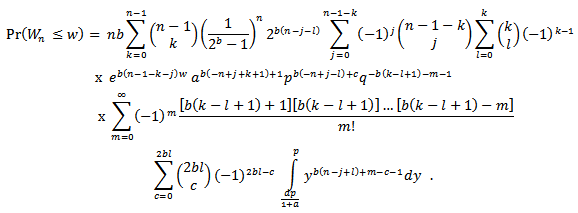 We then integrate and substitute the intervals to get,
We then integrate and substitute the intervals to get,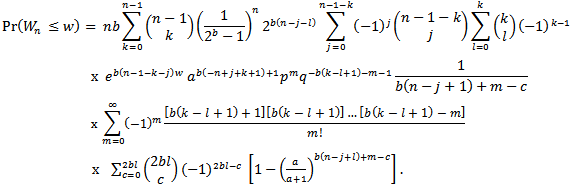 | (2.4) |
Substitute 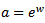 into equation (2.4) to get
into equation (2.4) to get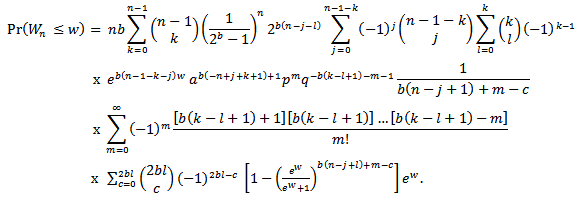 | (2.5) |
By differentiating the distribution function of the sample range in (2.5) with respect to w, we derive the pdf of 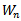 as
as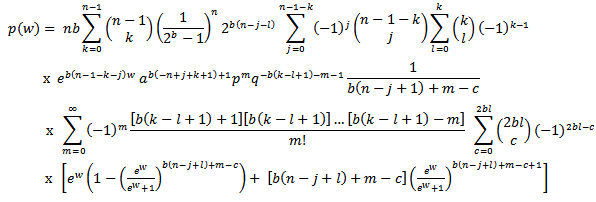 | (2.6) |
3. Distribution of the Quasi-Range
The sample rth quasi-range denoted by W, is defined as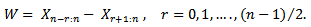 | (3.1) |
where n is odd. Thus the joint pdf of 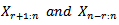 is
is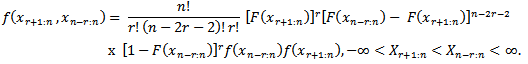 | (3.2) |
Since 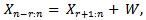 we have
we have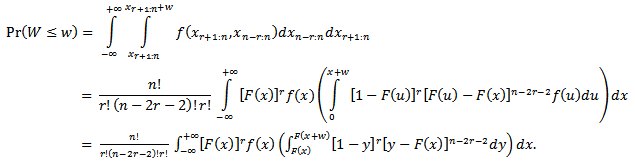 | (3.3) |
Integrating the expression in braces r times by parts, we have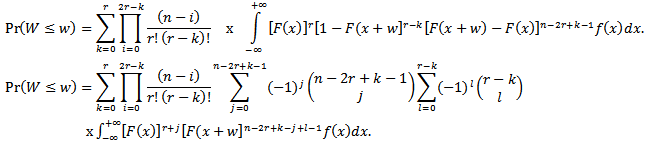 | (3.4) |
Let 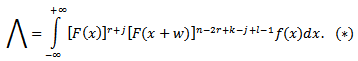 Substitute equations (1.3) and (1.4) in (*), we have
Substitute equations (1.3) and (1.4) in (*), we have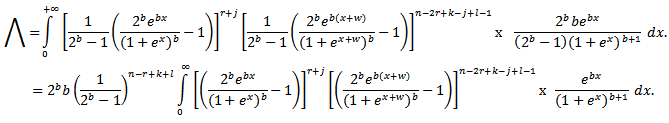 Since
Since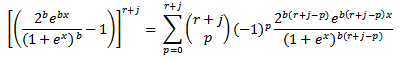 and
and 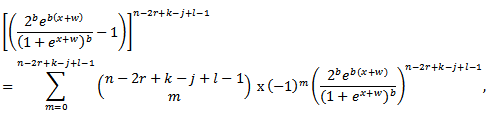 so, we have
so, we have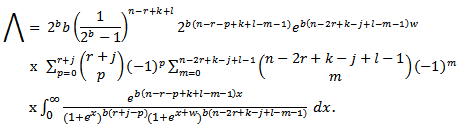 | (3.5) |
Now consider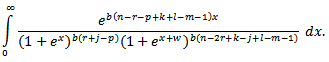 Let
Let 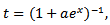 where
where 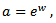 then
then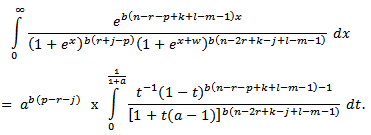 Let
Let 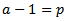 and
and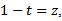 then with the intervals
then with the intervals 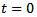 when
when 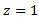 and
and 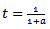 when
when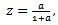 we have
we have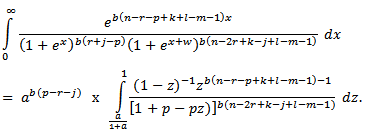 Let
Let 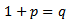 and
and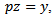 then we have
then we have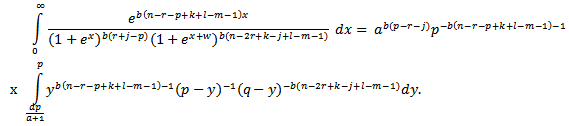 Since
Since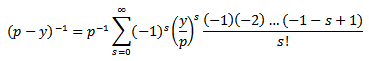 and
and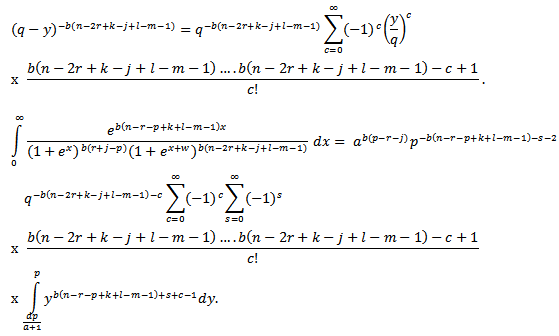 We then integrate and substitute the intervals to get,
We then integrate and substitute the intervals to get,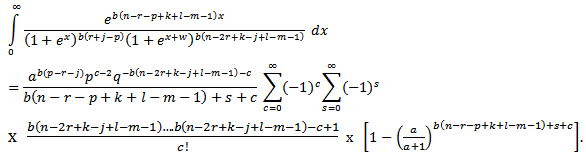 | (3.6) |
Substitute (3.6) into (3.5) to get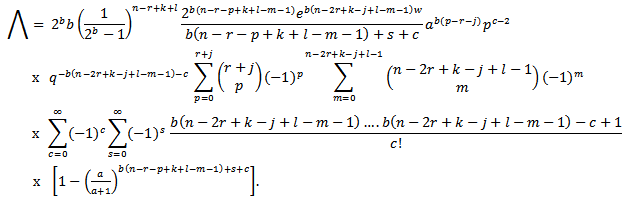 | (3.7) |
Substitute (3.7) into 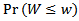 to get
to get | (3.8) |
Substitute  into (3.8) to get
into (3.8) to get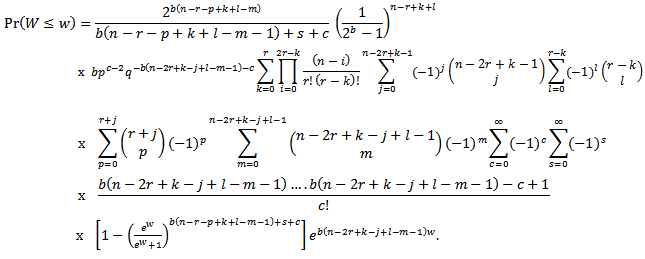 | (3.9) |
By differentiating the distribution function of the sample quasi-range in (3.9) with respect to w, we derive the pdf of W as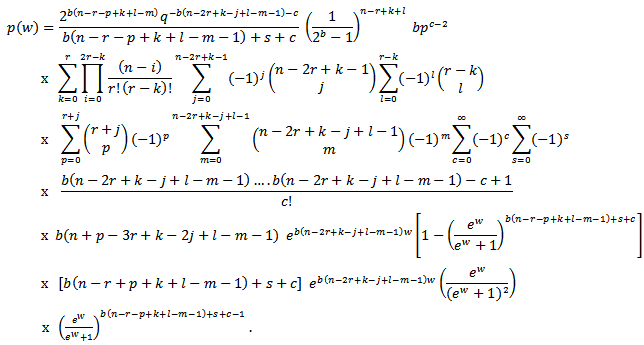 | (3.10) |
4. Conclusions
The distribution functions of the range and the quasi-range of the type II generalized half logistic distribution have been theoretically established in this paper.
References
| [1] | Balakrishnan, N. (1985). “Order Statistics from the Half-Logistic Distribution” Journal of Statistics and Computer Simulation. Vol. 20 pp 287-309. |
| [2] | Balakrishnan, N. and Puthenpura, S. (1986). “Best Linear Unbiased Estimators of Location and Scale Parameters of Half-Logistic Distribution” Journal of Statistical Computation and Simulation. Vol. 25 pp 193-204. |
| [3] | Balakrishnan, N. Wong, K.H.T. (1991). Approximate MLEs for the Location and Scale Parameters of the Half-Logistic Distribution with Type-H Right-Censoring. IEEE Transaction on Reliability. Vol. 40 No. 2 pp 140-145. |
| [4] | David H.A. (1970). Order Statistics John Wiley, New York. |
| [5] | Gupta, S.S. and Shah, B.K. (1965). Exact Moments and Percentage Points of the Order Statistics and the Distribution of the Range from the Logistic Distribution. Annals of Mathematics Statistics, 36, 907-920. |
| [6] | Olapade, A.K. (2003). On Characterizations of the Half Logistic Distribution. Inter. Stat., February Issue, No. 2. http://interstat.stat.vt.edu/InterStat/ARTICLES/2003articles/F06002.pdf. |
| [7] | Olapade, A.K. (2009). On Type II Generalized Half Logistic Distribution. Journal of Statistical Science, Volume 1, No. 1, pages 63-69. |
| [8] | Olapade, A.K. (2010). On the Distribution Functions of the Range and Quasi-Range for the Extended Type I Generalized Logistic Distribution. Journal of Statistical Research of Iran, Vol. 7, No. 1, pages 11-20. |
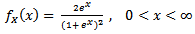
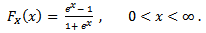
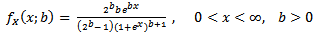
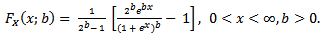
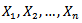 of size n coming from the type II generalized half logistic distribution and let
of size n coming from the type II generalized half logistic distribution and let 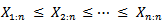 be the corresponding order statistics. Let
be the corresponding order statistics. Let 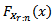 and
and 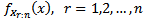 be the cdf and pdf of the rth order statistics
be the cdf and pdf of the rth order statistics 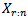 respectively. David (1970) obtained the pdf of
respectively. David (1970) obtained the pdf of 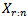 as
as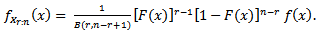
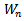 by
by 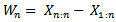 The cdf of
The cdf of 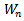 can be written as shown in Gupta and Shah (1965)
can be written as shown in Gupta and Shah (1965)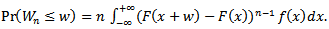
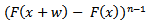 , we have
, we have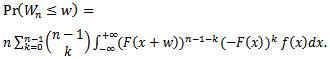
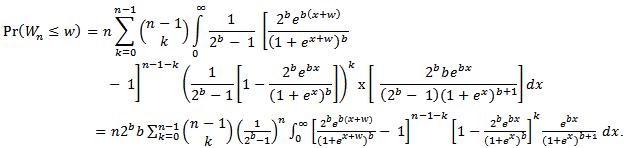 Since
Since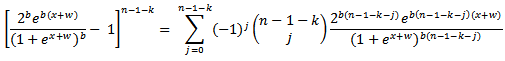 and
and 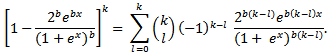 Therefore,
Therefore,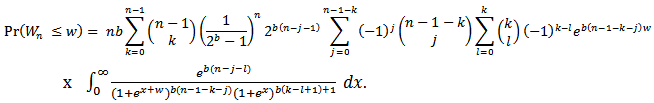
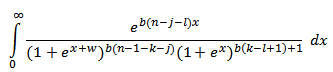 with the following transformations. Let
with the following transformations. Let 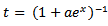 , where
, where 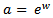 , then
, then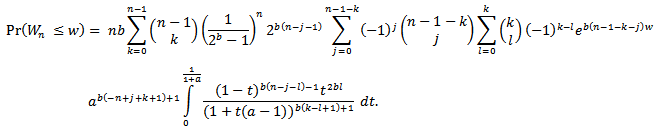 Let
Let 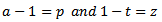 then with the intervals:
then with the intervals: 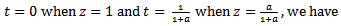
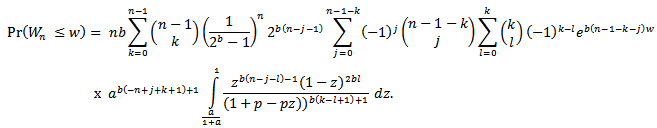 Let
Let 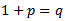 and
and 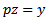 , then we have
, then we have 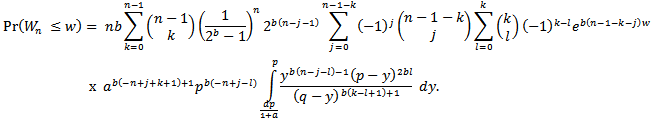
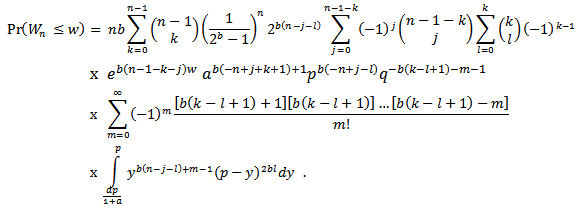 Since
Since 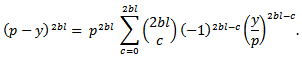 We have
We have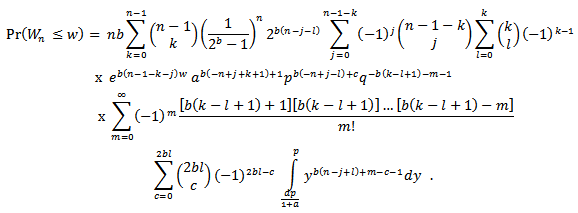 We then integrate and substitute the intervals to get,
We then integrate and substitute the intervals to get,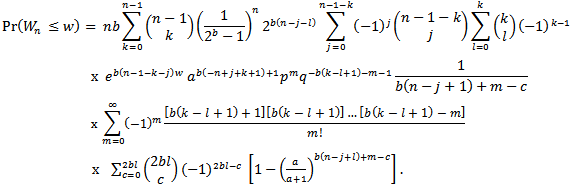
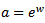 into equation (2.4) to get
into equation (2.4) to get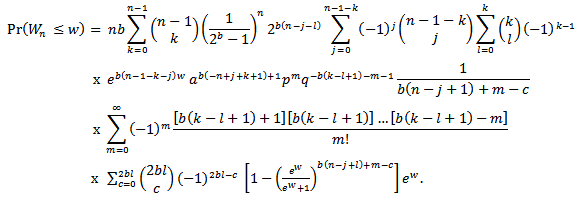
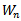 as
as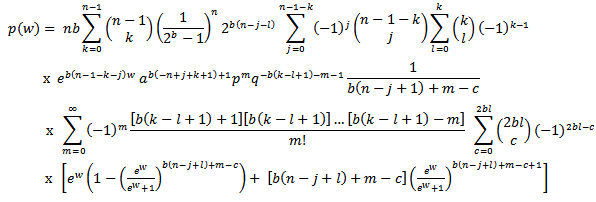
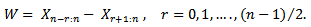
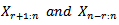 is
is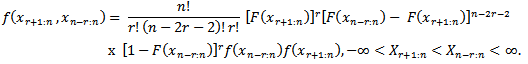
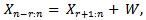 we have
we have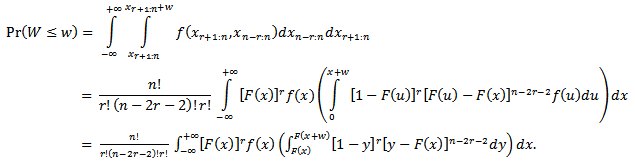
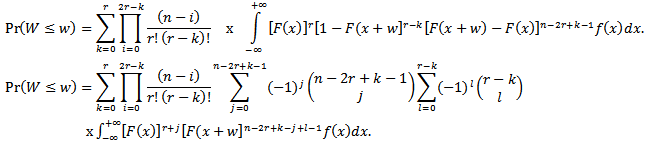
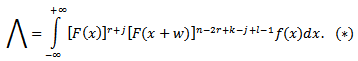 Substitute equations (1.3) and (1.4) in (*), we have
Substitute equations (1.3) and (1.4) in (*), we have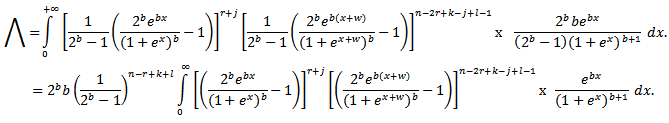 Since
Since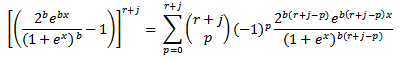 and
and 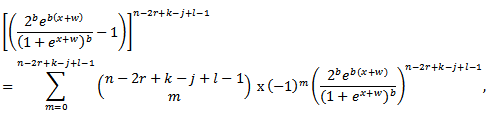 so, we have
so, we have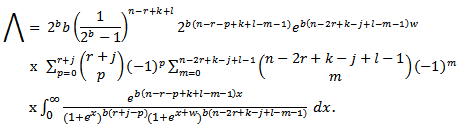
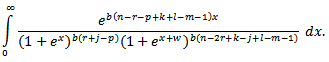 Let
Let 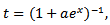 where
where 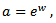 then
then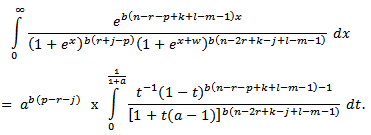 Let
Let 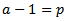 and
and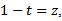 then with the intervals
then with the intervals 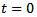 when
when 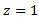 and
and 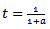 when
when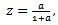 we have
we have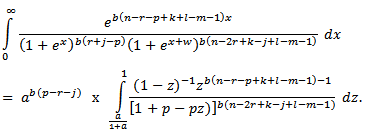 Let
Let 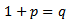 and
and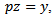 then we have
then we have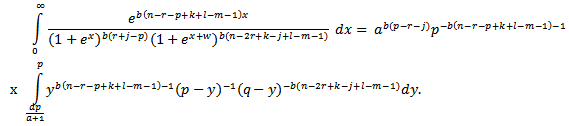 Since
Since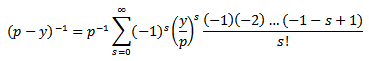 and
and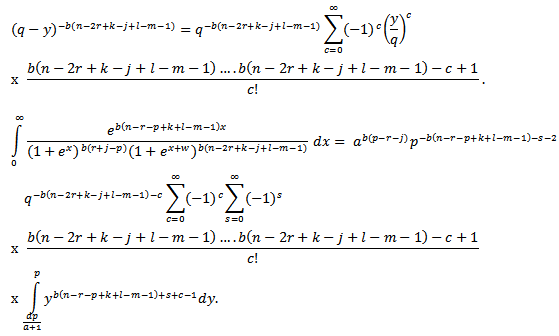 We then integrate and substitute the intervals to get,
We then integrate and substitute the intervals to get,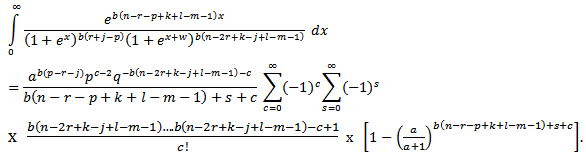
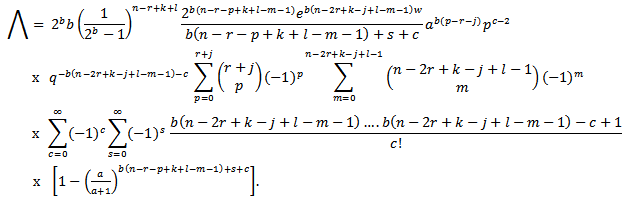
 to get
to get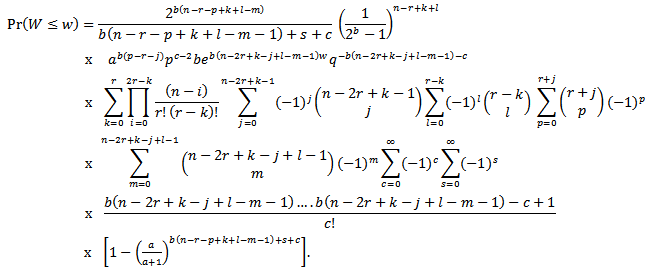
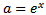 into (3.8) to get
into (3.8) to get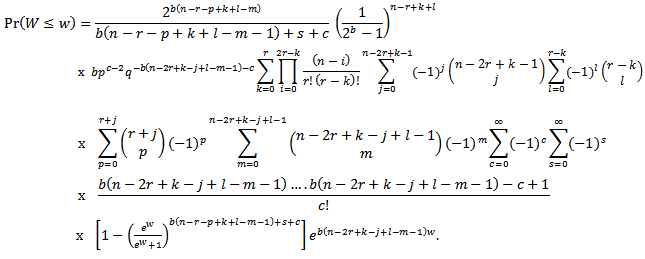
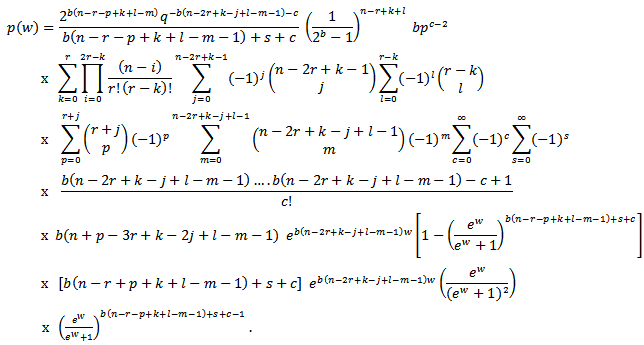
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML