-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2014; 4(5): 222-230
doi:10.5923/j.ajms.20140405.03
Robust Asymptotically Stabilization of Special Uncertain Descriptor Fractional-Order Systems with Fractional Feedback Control
Sameer Qasim Hasan, Ala Muhsien Abd
Department of Mathematics, Almustansiriyah University, Baghdad, Iraq
Correspondence to: Sameer Qasim Hasan, Department of Mathematics, Almustansiriyah University, Baghdad, Iraq.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
In this paper we investigate the asymptotically stabilization of a special type of singular fractional order belongs to interval (0,1) with uncertain parameter as time-invariant and norm-bounded appearing in the state matrix and suitable feedback fractional control by using Dynamics decomposition form.
Keywords: Fractional order, Descriptor system, Fractional, System, Fractional control, Feedback control
Cite this paper: Sameer Qasim Hasan, Ala Muhsien Abd, Robust Asymptotically Stabilization of Special Uncertain Descriptor Fractional-Order Systems with Fractional Feedback Control, American Journal of Mathematics and Statistics, Vol. 4 No. 5, 2014, pp. 222-230. doi: 10.5923/j.ajms.20140405.03.
1. Introduction
- Recently, fractional-order control systems have attracted increasing interest [15, 9, 11]. On the one hand, this is mainly due to the fact that many real-world physical systems are well characterized by fractional-order state equations [15], i.e., equations involving the so-called fractional derivatives and integrals. On the other hand, with the success in the synthesis of real noninteger differentiators and the emergence of a new electrical circuit element called “fractance” [10, 21], fractional-order controllers [16, 18, 12] have been designed and applied to control a variety of dynamical processes, including integer-order and fractional-order systems, so as to enhance the robustness and performance of the control systems. Singular fractional systems (known as generalized, descriptor of Fractional systems) describe a large class of systems, which are not only theoretical interest but also have a great importance in practice.Stability is fundamental to all control systems, certainly including fractional-order control systems [20, 19]. Recently, stability and stabilization problems of fractional-order linear time-invariant interval systems have been investigated in [1], [2, 4]. For example, for fractional-order linear time-invariant interval systems described in the transfer function form, the stability issue was discussed first in [13] and then further in [14]. In this paper we consider the problem of the robust asymptotical Stabilization for uncertain descriptor fractional-order systems.The descriptor multi-fractional-order systems by applying a derivative multi-controller and a state feedback.Controller is given to achieve the robust asymptotical stabilization of the obtained two sub system, first is fractional-order systems and the second is zero state.We using canonical form for the descriptor fractional-order systems and by applying a derivative controller and a state feedback controller is given to achieve the robust asymptotical stabilization of the fractional-order systems.In section II, the paper are organized as follow in section II, we introduce the definition of fractional derivative in brief; we present also some mathematical results. In section III, we propose robust linear uncertainty descriptor multi-fractional controller for the stabilization of system.
2. Preliminaries
- A. Some definitionNow we review some important and definition:The Caputo derivative on the other, defined [17],
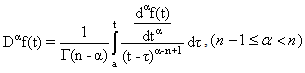 For
For 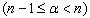 and
and 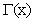 is the well-known Euler’s gamma function.Definition (2.1), [22]:Let
is the well-known Euler’s gamma function.Definition (2.1), [22]:Let 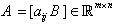 ,
, 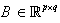 . Their Kronecker product (i.e., the direct product or tensor product), denoted as
. Their Kronecker product (i.e., the direct product or tensor product), denoted as 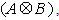 is defined by
is defined by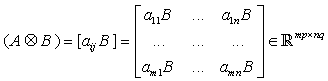 Now we consider the fractional –order linear system.
Now we consider the fractional –order linear system.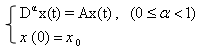 | (1) |
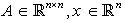 is the state vector.The system (1) is stable if the condition is satisfied
is the state vector.The system (1) is stable if the condition is satisfied 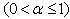 [5], with the condition(2),
[5], with the condition(2), 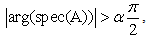 | (2) |
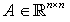 and
and 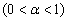 . The fractional- order system
. The fractional- order system 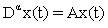 is asymptotically stable that means
is asymptotically stable that means 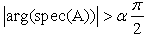 if and only if there exist two real symmetric matrices
if and only if there exist two real symmetric matrices 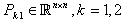 and two skew-symmetric matrices where
and two skew-symmetric matrices where 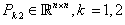 such that
such that 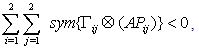
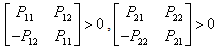 where
where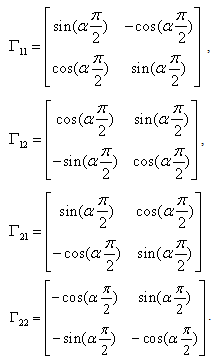 Lemma (2.2), [7]:For any matrices X and Y with appropriate dimensions, we have
Lemma (2.2), [7]:For any matrices X and Y with appropriate dimensions, we have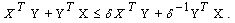 For any
For any 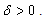 Remark (2.1), [5]:Consider the singular fractional linear system
Remark (2.1), [5]:Consider the singular fractional linear system 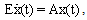 if the following conditions hold:i. the matrix pair (E, A) is regular .ii. the matrix pair (E, A) is regular an impulse free. Then there exist there two invertible matrices.
if the following conditions hold:i. the matrix pair (E, A) is regular .ii. the matrix pair (E, A) is regular an impulse free. Then there exist there two invertible matrices. 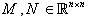 Satisfying:
Satisfying: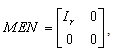
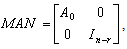 where
where 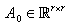 is an invertible,
is an invertible, 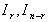 are the identity matrices of dimensions r, n-r respectively.Definition (2.2), [5, 6]:i. A matrix pair (E, A) is called regular if E and A are square and
are the identity matrices of dimensions r, n-r respectively.Definition (2.2), [5, 6]:i. A matrix pair (E, A) is called regular if E and A are square and 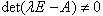 for some value
for some value 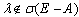 it is called singular otherwise. Where
it is called singular otherwise. Where 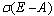 is the set of all Finite Spectrum Eigenvalues.ii. The matrix pair (E, A) is said to be impulse free if
is the set of all Finite Spectrum Eigenvalues.ii. The matrix pair (E, A) is said to be impulse free if 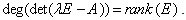
3. The Main Result
- The singular linear fractional order uncertainty control system
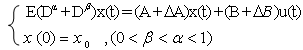 | (3) |
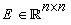 is the singular matrix,
is the singular matrix, 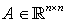 ,
, 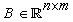 ,
, 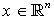 is the semi-state vector,
is the semi-state vector, 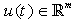 is the input vector,
is the input vector, 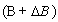 is invertible and
is invertible and 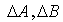 are time-invariant matrix representing norm-bounded parameter uncertainty, with the following conditions:i. The singular matrix E has the form, where nonsingular matrix
are time-invariant matrix representing norm-bounded parameter uncertainty, with the following conditions:i. The singular matrix E has the form, where nonsingular matrix 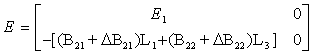
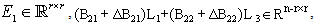
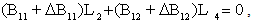
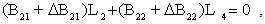 defined in (iii) and equation (7) later on.ii.
defined in (iii) and equation (7) later on.ii. 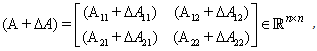 where
where 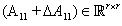 ,
, 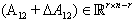 ,
,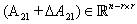
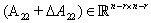 , such that
, such that 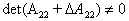 iii.
iii. 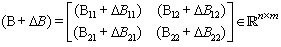 , is invertible, where
, is invertible, where 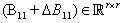 ,
,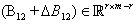
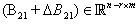 ,
,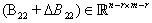 iv.
iv. 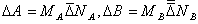 where
where 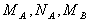 and
and 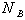 are known real constant matrices of appropriate dimensions, and the uncertain matrices
are known real constant matrices of appropriate dimensions, and the uncertain matrices 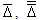 satisfies
satisfies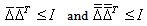 | (5) |
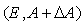 is regular and impulse free. Consider the feedback control for system (3) in the following form
is regular and impulse free. Consider the feedback control for system (3) in the following form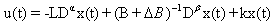 | (6) |
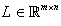 has the form
has the form 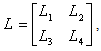 | (7) |
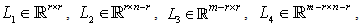 and
and 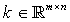 are gain matrices such that,
are gain matrices such that,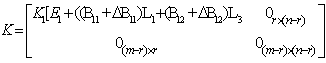 | (8) |
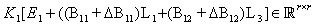 and
and 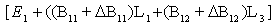 is invertible matrix. We substituting (6) into system (3), we obtain
is invertible matrix. We substituting (6) into system (3), we obtain 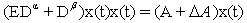
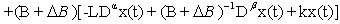 We have
We have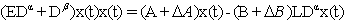
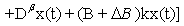 We gets
We gets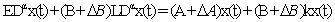 We obtain
We obtain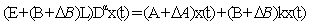 | (9) |
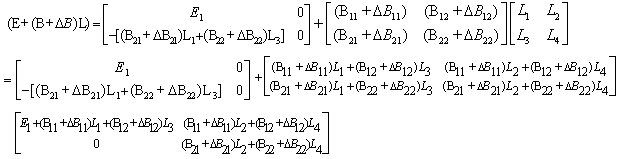 By condition (i), we have
By condition (i), we have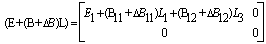 | (10) |
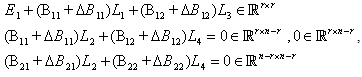 The right side of equation (9) has the form
The right side of equation (9) has the form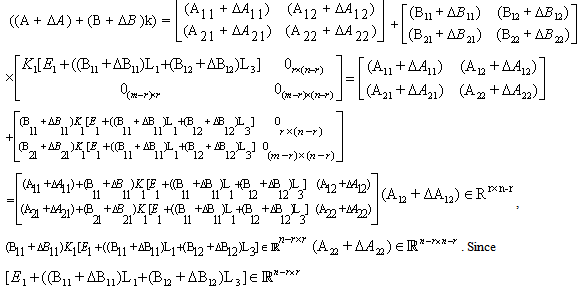 | (11) |
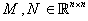 satisfying:
satisfying: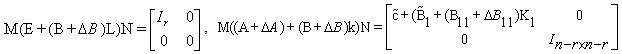 | (12) |
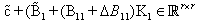 is an invertible which defined later on. One can get:
is an invertible which defined later on. One can get: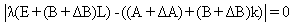 Then
Then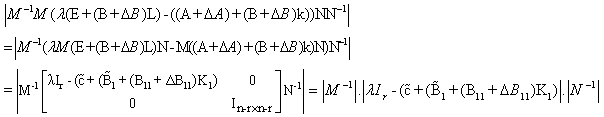 Since
Since 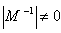 and
and 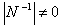 , hence the finite eigenvalue
, hence the finite eigenvalue 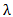 of the matrix pair
of the matrix pair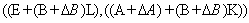 is also an eigenvalue of matrix
is also an eigenvalue of matrix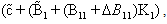 with
with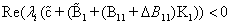
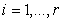 We assume that M and N has the forms:
We assume that M and N has the forms: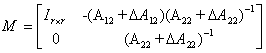 where
where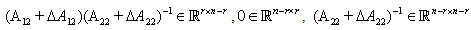 and
and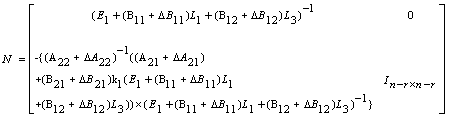 Where
Where 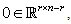
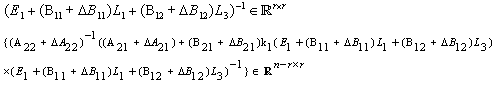 We obtain
We obtain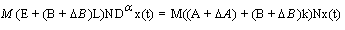 By using M and N, we have
By using M and N, we have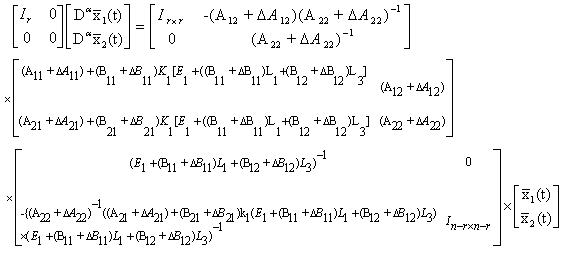 | (13) |
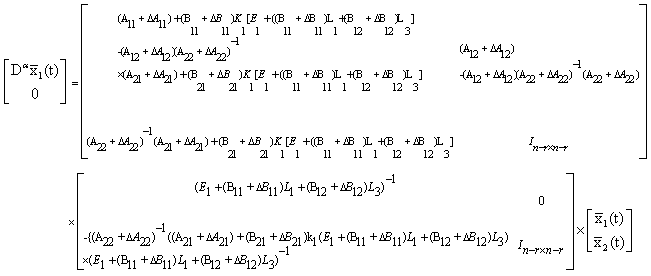 We have
We have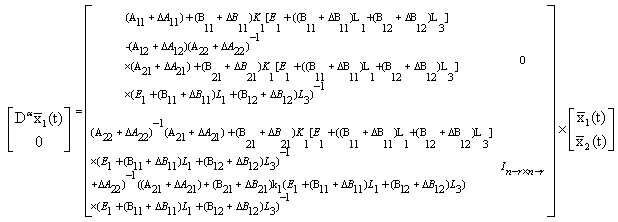 | (14) |
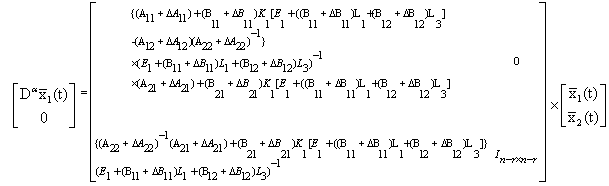 Then we have
Then we have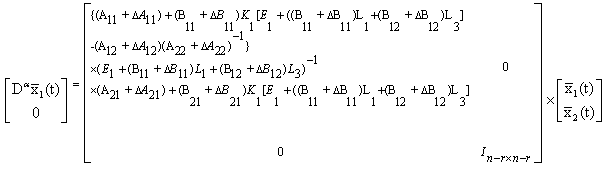 We obtain
We obtain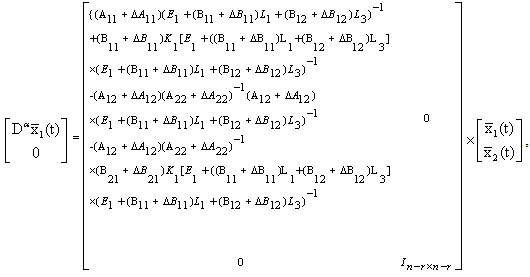 We have
We have 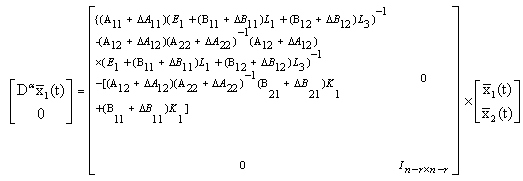 We have
We have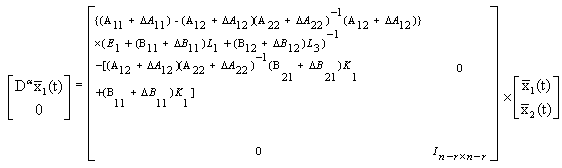 | (15) |
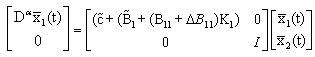 | (16) |
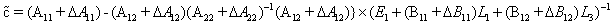
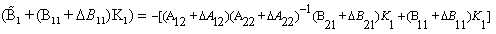 also
also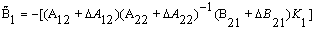 Then, we have
Then, we have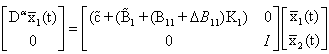 One can get
One can get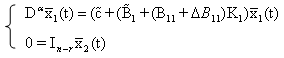 We have
We have
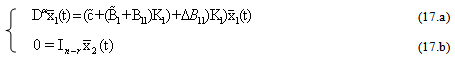 We obtain the formula as follows:
We obtain the formula as follows:
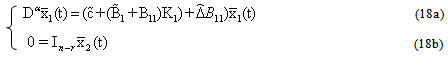 where
where 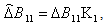 The design of the gain matrix K which robustly stabilization the descriptor fractional-order system (3) for the fractional order
The design of the gain matrix K which robustly stabilization the descriptor fractional-order system (3) for the fractional order 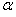 belonging to (18.a),
belonging to (18.a), 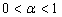 are derived.Theorem (3.1)Assume that (3) is regular and impulse free, then there exists again matrix
are derived.Theorem (3.1)Assume that (3) is regular and impulse free, then there exists again matrix 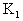 such that descriptor fractional order (3) with fractional-order
such that descriptor fractional order (3) with fractional-order 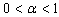 controlled by the control (6) is asymptotically stable, if there exist matrices
controlled by the control (6) is asymptotically stable, if there exist matrices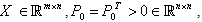 and two real scalars
and two real scalars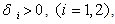 such that
such that 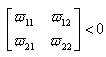 | (19) |
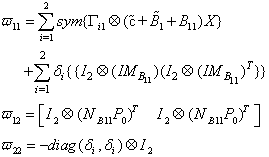
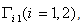 Satisfy Lemma (2.1).Proof:-Under the assumption regular and impulse free that system(3), then there exists a gain matrix L such that system (3)can be written in the form (18), in this case the matrix K can be determined from the stability of system (18).It follows from Lemma (2.1) that
Satisfy Lemma (2.1).Proof:-Under the assumption regular and impulse free that system(3), then there exists a gain matrix L such that system (3)can be written in the form (18), in this case the matrix K can be determined from the stability of system (18).It follows from Lemma (2.1) that 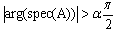 is equivalent to
is equivalent to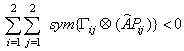 | (20) |
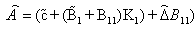 and
and 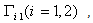 Satisfy Lemma (2.1). By assume
Satisfy Lemma (2.1). By assume 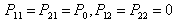 in (20) one can conclude that
in (20) one can conclude that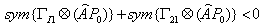 | (21) |
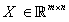 and
and 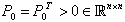 , Such that
, Such that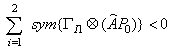 | (22) |
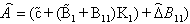 in (22) with
in (22) with 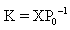 we obtain
we obtain 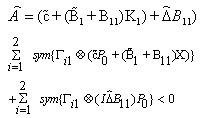 | (23) |
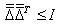 , then we obtain
, then we obtain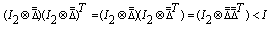 | (24) |
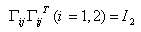 Then by (24) and Lemma (2.2) that for any real scalar
Then by (24) and Lemma (2.2) that for any real scalar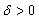
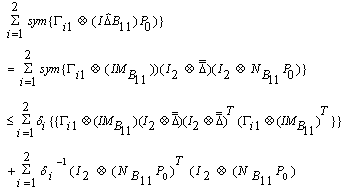 | (25) |
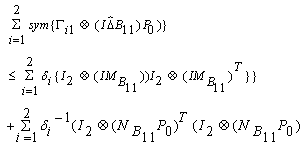 | (26) |
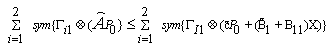 | (27) |
4. Conclusions
- The necessary conditions of robust asymptotically stabilization for special Uncertain singuler fractional-order systems with feedback fractional control for the fractional order α belonging to
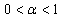 with parameter uncertainties in the state matrix have been given in details . The problem of canonical of descriptor fractional-order systems by derivative fractional controller has been proposed with implosive free condition.
with parameter uncertainties in the state matrix have been given in details . The problem of canonical of descriptor fractional-order systems by derivative fractional controller has been proposed with implosive free condition.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML