-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2014; 4(4): 191-194
doi:10.5923/j.ajms.20140404.03
Action of the Universal Hausdorff Group
Abid A. Al-Ta'ai1, Hussein Faiq Saddam2
1Department of Mathematics, College of science, Al-Mustansiriya University, Baghdad, Iraq
2Department of Mathematics, College of Education, Al-Mustansiriya University, Baghdad, Iraq
Correspondence to: Abid A. Al-Ta'ai, Department of Mathematics, College of science, Al-Mustansiriya University, Baghdad, Iraq.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The main aim of this paper is to construct an action of the universal hausdorff group of some topological group acting on a 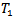 -space, For any topological group acting on some
-space, For any topological group acting on some 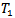 topological space we induce an action of the universal hausdorff group on that space, and study some of the properties of this action.
topological space we induce an action of the universal hausdorff group on that space, and study some of the properties of this action.
Keywords: Topological group, Group action, Universal hausdorff group, Continuous action, Proper action
Cite this paper: Abid A. Al-Ta'ai, Hussein Faiq Saddam, Action of the Universal Hausdorff Group, American Journal of Mathematics and Statistics, Vol. 4 No. 4, 2014, pp. 191-194. doi: 10.5923/j.ajms.20140404.03.
Article Outline
1. Introduction
- A topological group is one of the most interesting topics. Equipped with two compatible structures (group and topology), it admits a beautiful set of properties that are not readily available in either of the two structures separately. One of which is the universal hausdorff group which is the quotient of the closure of the identity element.A topological group is a set G on which two structures are given, a group structure and a topology, such that the group operations are compatible. Specifically, the mapping
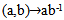 from the direct product
from the direct product 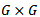 into G must be continuous. A subgroup H of a topological group G is a topological group in the with respect to the relative topology. The quotient space of cosets is given the quotient topology with respect to the canonical mapping from G onto G/H. If H is a normal subgroup of G, then G/H (the quotient group of G by H) is a topological group. Taking the closure of the identity we get a normal subgroup of the topological group and hence we get a topological group of the resulting quotient group, this group is the main focus of this study.Continuous action of a topological group is simply a group action which is also continuous. Continuity of the action map can give extra properties to both of the topological and algebraic structures, which is a fact well used in this paper.This research consists of four section; section one consist the basic definition of topological group, hausdorff topological space,…etc. in section two we study the universal hausdorff group also given some theorems and lemma. In section three we study the Continuous Action of Topological Group, in section fourwe study Continuous Action of Topological Groups and induced an action of the universal hausdorff group on that space.
into G must be continuous. A subgroup H of a topological group G is a topological group in the with respect to the relative topology. The quotient space of cosets is given the quotient topology with respect to the canonical mapping from G onto G/H. If H is a normal subgroup of G, then G/H (the quotient group of G by H) is a topological group. Taking the closure of the identity we get a normal subgroup of the topological group and hence we get a topological group of the resulting quotient group, this group is the main focus of this study.Continuous action of a topological group is simply a group action which is also continuous. Continuity of the action map can give extra properties to both of the topological and algebraic structures, which is a fact well used in this paper.This research consists of four section; section one consist the basic definition of topological group, hausdorff topological space,…etc. in section two we study the universal hausdorff group also given some theorems and lemma. In section three we study the Continuous Action of Topological Group, in section fourwe study Continuous Action of Topological Groups and induced an action of the universal hausdorff group on that space.2. Basic Concepts
- Definition 1.1 [6]: A topological group is a set G th two structures:i. G is a group,ii. G is a topological space,Such that the two structures are compatible i.e., the multiplication map
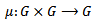 nd the inversion map
nd the inversion map 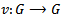 are both continuous.Definition 1.2 [6]: amorphism of topological groups
are both continuous.Definition 1.2 [6]: amorphism of topological groups 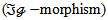 is a continuous group homomorphism.Notation: if G is a topological group
is a continuous group homomorphism.Notation: if G is a topological group 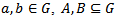 then:
then: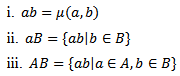 Remark 1.3: The maps
Remark 1.3: The maps 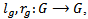 defined by
defined by 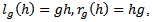 are homeomorphisms (not necessarily a homomorphism) called left and right translation respectively.Definition 1.4 [3]: a subgroup H of a group G is a normal subgroup of G if for every
are homeomorphisms (not necessarily a homomorphism) called left and right translation respectively.Definition 1.4 [3]: a subgroup H of a group G is a normal subgroup of G if for every 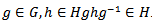 .Definition 1.5 [3]: If G is a group, H is a normal subgroup, then the collection of cosets of H denoted by G/H is a group called the quotient group.Remark 1.6: If H is a normal subgroup of G hen it is also a topological group, and the quotient map is both continuous and open.Remark 1.7: Let
.Definition 1.5 [3]: If G is a group, H is a normal subgroup, then the collection of cosets of H denoted by G/H is a group called the quotient group.Remark 1.6: If H is a normal subgroup of G hen it is also a topological group, and the quotient map is both continuous and open.Remark 1.7: Let 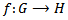 in
in 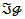 has kernel K and image
has kernel K and image 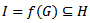 with quotient map
with quotient map 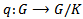 and inclusion map
and inclusion map 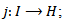 then
then 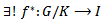 in
in 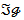 such that
such that 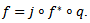 The map
The map 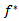 is a bijection and if
is a bijection and if 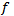 is open or closed it is a
is open or closed it is a 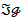 - iisomorphism.Definition 1.8 [2]: a topological space X is a
- iisomorphism.Definition 1.8 [2]: a topological space X is a 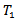 space if every singleton subset of
space if every singleton subset of 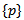 of X is closed.Definition 1.9 [4]: a topological space X is Hausdorff if each pair of distinct points
of X is closed.Definition 1.9 [4]: a topological space X is Hausdorff if each pair of distinct points 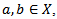 belong respectively to disjoint open sets.Definition 1.10 [2]: a subset A of a topological space X is compact if every cover of A is reducible to a finite cover.
belong respectively to disjoint open sets.Definition 1.10 [2]: a subset A of a topological space X is compact if every cover of A is reducible to a finite cover.3. The Universal Hausdorff Group
- Theorem 2.1 [6]: let G e a topological group, E is the closure of the identity element e, then E is a normal subgroup of G.Proof:
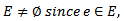 Now if
Now if 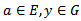 then
then 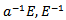 and
and 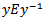 are closed sets containing e and hence contain E.Also if
are closed sets containing e and hence contain E.Also if 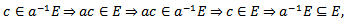 again if
again if 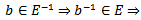
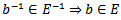
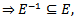 then
then 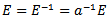 so that E is a group.Normality follows for if
so that E is a group.Normality follows for if 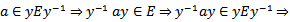
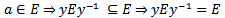 Lemma 2.2: let
Lemma 2.2: let 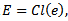 then E has the property that if A is any closed set, then
then E has the property that if A is any closed set, then 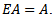 Proof: let
Proof: let 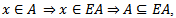 Suppose that
Suppose that 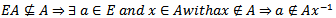 but
but 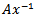 is a closed set containing e then
is a closed set containing e then 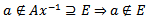 which is a contradiction hence
which is a contradiction hence 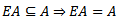 .Theorem 2.3: let
.Theorem 2.3: let 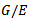 be the quotient group induced by E, then
be the quotient group induced by E, then 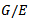 has the property that if
has the property that if 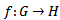 is in
is in 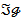 , where H is Hausdorff1,
, where H is Hausdorff1, 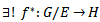 in
in 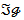 such that
such that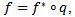 where
where 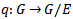 is the quotient map.
is the quotient map.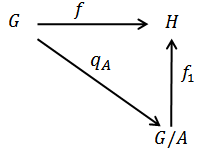 Proof: let
Proof: let  then A is a closed normal subgroup of G so that by lemma 2.2
then A is a closed normal subgroup of G so that by lemma 2.2  Now A has the universal property that
Now A has the universal property that  such that
such that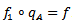 .Define
.Define 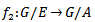 by
by 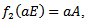 we shall show that
we shall show that 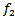 is well defined.Let
is well defined.Let 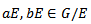 such that
such that 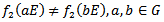 we must show that
we must show that 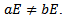 Now
Now 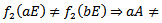
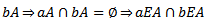
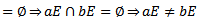 so that
so that 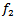 is well defined.Also
is well defined.Also 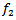 is a group homomorphism for if
is a group homomorphism for if 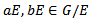 we have
we have 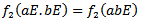
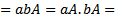
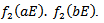 Also we have
Also we have 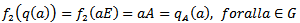 so that
so that 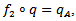 and hence we have if
and hence we have if 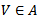 is open we have
is open we have 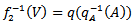 and considering the fact that
and considering the fact that 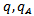 are continuous and open maps respectively we have
are continuous and open maps respectively we have 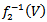 is open so that
is open so that 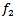 is continuous and hence a
is continuous and hence a 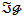 -morphism.Set
-morphism.Set 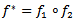 then for all
then for all 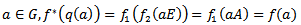 so that
so that 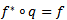 , also being the composition of
, also being the composition of  -morphism,
-morphism, 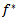 is a
is a 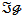 -morphism.Uniqueness follows for if
-morphism.Uniqueness follows for if 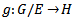 such that
such that 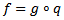 then for all
then for all 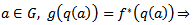
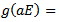
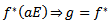
 Definition 2.4:
Definition 2.4: 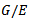 as stated above is called the universal Hausdorff group.
as stated above is called the universal Hausdorff group.4. Continuous Action of Topological Groups
- Definition. 3.1 [4]: Let G be a group and X a set. An action of G on M is a map
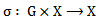 satisfying:i.
satisfying:i. 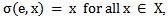 andii.
andii. 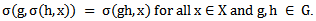 Definition 3.2 [1]: A topological group action is a group action such that the map
Definition 3.2 [1]: A topological group action is a group action such that the map 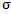 is continuous.Definition 3.3 [5] A continuous action is said to be proper if the map
is continuous.Definition 3.3 [5] A continuous action is said to be proper if the map 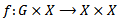 defined by
defined by 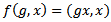 is a proper map, that is inverse of compact sets is compact.Definition 3.4 [5]: An action is said to be faithful if for any
is a proper map, that is inverse of compact sets is compact.Definition 3.4 [5]: An action is said to be faithful if for any 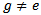 in G there exist an x in X such that
in G there exist an x in X such that 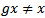 .Theorem. 3.5: let
.Theorem. 3.5: let 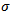 be a topological group G action on the
be a topological group G action on the 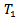 space X then the stabilizer of any point in X is a closed subset of G, i.e.
space X then the stabilizer of any point in X is a closed subset of G, i.e. 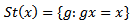 is closed for all
is closed for all 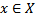 .Proof: since the action map is continuous then the restriction map
.Proof: since the action map is continuous then the restriction map 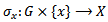 is continuous,Now the pre-image of the point x is the set
is continuous,Now the pre-image of the point x is the set 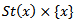 which is a closed subset of
which is a closed subset of 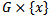 . But the map
. But the map 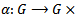
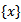 defined by
defined by 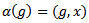 is also continuous, so that the pre-image of the set
is also continuous, so that the pre-image of the set 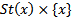 is just
is just 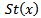 and hence
and hence 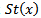 is closed.
is closed.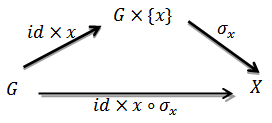 Corollary: The kernel
Corollary: The kernel 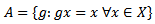 of a continuous action on a
of a continuous action on a 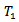 space X is a closed normal subgroup of G.Proof: by theorem. 3.2 we have
space X is a closed normal subgroup of G.Proof: by theorem. 3.2 we have 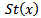 is closed in G so that
is closed in G so that 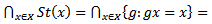
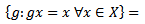
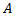 is closed in G. Also being the kernel of the homomorphism
is closed in G. Also being the kernel of the homomorphism 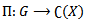 (the space of all homeomorphisms
(the space of all homeomorphisms 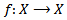 ), then A is a normal subgroup of G.Remark 3.6: A, as defined above, has the universal property that the quotient space
), then A is a normal subgroup of G.Remark 3.6: A, as defined above, has the universal property that the quotient space 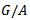 also acts continuously on the space X. this action is faithful and is given by
also acts continuously on the space X. this action is faithful and is given by 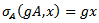 .
.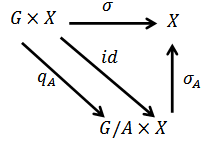
5. Action of the Universal Hausdorff Group
- Further next we shall construct an action of the universal hausdorff group.Remark 4.1: if G is a topological group acting on the
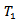 space X then as in the above remark we get an action of the quotient of the kernel of the action, also we obtain, as in theorem 2.3 a continuous homomorphism
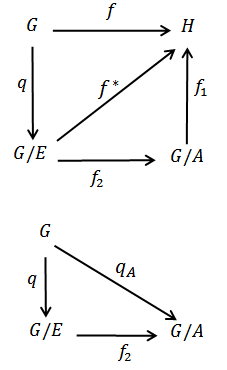
space X then as in the above remark we get an action of the quotient of the kernel of the action, also we obtain, as in theorem 2.3 a continuous homomorphism 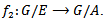 Theorem 4.2: let G be a topological group acting on the
Theorem 4.2: let G be a topological group acting on the 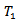 space X, E is the universal hausdorff group, then there is an action of the quotient group
space X, E is the universal hausdorff group, then there is an action of the quotient group 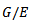 on the space X such that the diagram commute.
on the space X such that the diagram commute.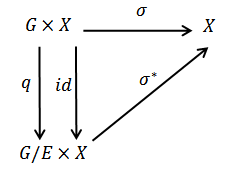 Proof: by the corollary of theorem 3.3 the kernel A of the action is a closed normal subgroup of G so that by lemma 2.2 we have
Proof: by the corollary of theorem 3.3 the kernel A of the action is a closed normal subgroup of G so that by lemma 2.2 we have 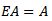 .Define
.Define 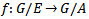 by
by 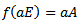 , we shall show that
, we shall show that  is well defined.
is well defined.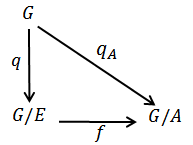 Let
Let 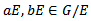 such that
such that 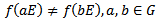 we must show that
we must show that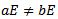 . Now
. Now 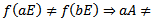
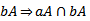
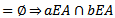
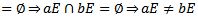 so that f is well defined.Also f is a group homomorphism for if
so that f is well defined.Also f is a group homomorphism for if 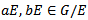 we have
we have 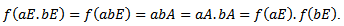 Now define
Now define 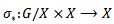 by
by 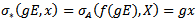 .We shall proof that
.We shall proof that 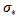 is an action map, considering the diagram below let
is an action map, considering the diagram below let 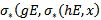
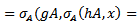
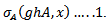 Also
Also 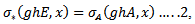 and by 1 and 2 we have
and by 1 and 2 we have 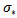
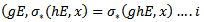 Furthermore
Furthermore 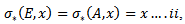 then by
then by 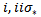 is a group action.Continuity follows from the fact that
is a group action.Continuity follows from the fact that 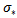 is the composition of the two continuous mappings
is the composition of the two continuous mappings 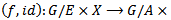
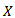 and
and 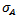 . Then
. Then 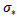 is a continuous action of
is a continuous action of 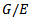 on X.Now
on X.Now 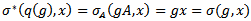 , this proofs that the diagram commute.
, this proofs that the diagram commute.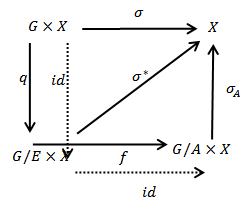 Theorem 4.3: if
Theorem 4.3: if 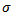 is an action of a topological group G on a
is an action of a topological group G on a 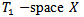 then the induced action of the universal hausdorff group is also proper.Proof: since the action of G is proper then the map
then the induced action of the universal hausdorff group is also proper.Proof: since the action of G is proper then the map 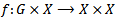 defined by
defined by 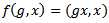 is proper.Now
is proper.Now 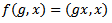 and
and 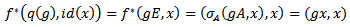 so that the below diagram commute, now let V be a compact subset of
so that the below diagram commute, now let V be a compact subset of 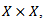 since f is proper then
since f is proper then 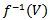 is compact in
is compact in 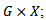 finally since
finally since 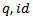 are continuous mappings then
are continuous mappings then  is compact making
is compact making  a proper map which in turn imply that
a proper map which in turn imply that  is a proper action.
is a proper action.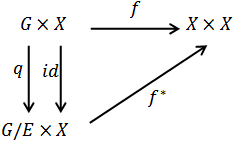 Remark 4.4: being also topological groups, everything we mentioned is also valid to Lie groups; however, lie groups and more generally Manifolds are often considered (by some authors) as Hausdorff spaces, a convention that imply that the closure of the identity is merely the trivial group, which means that the universal hausdorff group is equivalent to the topological group itself.
Remark 4.4: being also topological groups, everything we mentioned is also valid to Lie groups; however, lie groups and more generally Manifolds are often considered (by some authors) as Hausdorff spaces, a convention that imply that the closure of the identity is merely the trivial group, which means that the universal hausdorff group is equivalent to the topological group itself.6. Conclusions
- All group actions considered are continuous. For any topological group acting on a
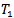 space the action of the universal hausdorff group have been constructed and proven to be continuous.
space the action of the universal hausdorff group have been constructed and proven to be continuous.Note
- 1. It is enough for the proof for H to be merely
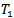 . However, for any topological group the property of being
. However, for any topological group the property of being 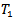 is equivalent to the property of being hausdorff.
is equivalent to the property of being hausdorff. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML