1. Introduction

Let R be a commutative ring and M a unital R-module. Gilmer [1, p.60] has been defined the concept of cancellation ideal to be the ideal I of R which satisfies the following:

Whenever AI = BI with A and B are ideals of R implies A = B. Mijbass in [2] has been generalized this concept to modules. He has been defined the cancellation modules as follows:

An R-module M is called a cancellation module whenever AM = BM with A and B are ideals of R implies A = B.

In this work we shall introduce the concept of purely cancellation module by using some restrictions on the ideals A and B in the above definition, namely we shall say that.

An R-module M is called purely cancellation, whenever AM = BM with A is a pure ideal of R and B is any ideal of R implies A = B.

An ideal A of a ring R is said to be pure if A ∩ B = BA for all ideal B of R, [3].

Clearly, the class of cancellation modules contains the class of purely cancellation modules and we can give an example to show that this inclusion is properly. However we shall give conditions under which the two classes are equivalent, see proposition (1.9).

This paper consists of two sections our principal aim in the first section is to study the purely cancellation modules. Moreover we study the relationships between cancellation modules and purely cancellation module. Also, we discuss the property of purely cancellation in each of the module and its trace, where we prove that a module is purely cancellation if its trace is a purely cancellation ideal, see corollary (1.12). Next, we study the property of purely cancellation in certain classes of modules see proposition (1.15), corollary (1.16), proposition (1.17) and proposition (1.18).

In the second section, we shall introduce the concept of weakly purely cancellation modules which is a generalization of purely cancellation modules, we shall discuss the validity of the results that we obtain in the first section.

2. Purely Cancellation Modules

In this section we introduce the concept of purely cancellation modules with some examples and basic properties about this concept. Also, we investigate purely cancellation module by using the trace of the module. Finally, we study the relation between purely cancellation modules and some types of modules.

Definition (1.1):

An R-module M is called purely cancellation whenever AM = BM, with A is a pure ideal of R and B is any ideal of R, implies A = B.

Examples and Remarks (1.2):

(1) Z₆ as a Z₁₂-module is purely cancellation module.

It is clear that 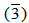is pure ideal of Z₁₂ and 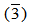Z₆ = 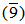Z₆. Then = .

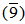(2) Every cancellation module is purely cancellation module, but the converse is not true in general, for example: Z₆ as a Z₁₂-module. See above example number 1. But Z₆ is not cancellation Z₁₂-module, since an n_R(Z₆) = 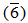is not faithful and hence Z₆ is not cancellation by [2,remark (1-4), p.8].

(3) Q as a Z-module is not purely cancellation module.

Since, (xZ)Q = Q for any pure ideal (xZ) in Z, x ≠ 1. Its clear that, (xZ)Q ⊆ Q.

Now, let t ∈ Q. Then 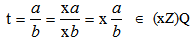where a, b ∈ Z. Implies Q ⊆ (xZ)Q. Therefore (xZ)Q = Q. Thus we get, Q is not purely cancellation module. However (xZ) ≠ Z.

(4) Z₅ as a Z₁₅-module is purely cancellation module. Since, 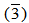is pure ideal of Z₁₅ and 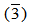Z₅ = 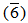Z₅. Then 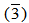= 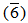. Also, 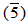is pure ideal of Z₁₅ and 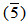Z₅ = 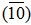Z₅. Then = .

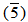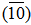Recall that the element m in an R-module M (where R is an integral domain) is called torsion element if there exists 0 ≠ r ∈ R such that rm = 0. And m is called a non-torsion element if rm ≠ 0, ∀ 0 ≠ r ∈ R, [2].

For cyclic modules we have the following result.

Proposition (1.3):

Every cyclic module generated by a non-torsion element is purely cancellation.

Proof: Let M = <m>, where m is a non-torsion element and A<m> = B<m>, where A is pure ideal of R and B is any ideal of R. am ∈ B<m> for all a ∈ A, then am = bm, where b ∈ B, implies am – bm = 0. Therefore (a – b)m = 0, but m is a non-torsion element, then a – b = 0, which implies a = b. Therefore A ⊆ B.

Similarly B ⊆ A, and hence A = B.

We shall show by an example that the condition M is generated by a non-torsion element in proposition (1.3) can not be dropped.

Example (1.4):

Let M = Z₂ as a Z₄-module, it is clear that Z₂ = 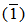and is a torsion element in Z₂ and Z₂ is not purely cancellation Z₄-module see examples and remark (1.2)(5).

In the following theorem we give some characterizations of purely cancellation modules.

Theorem (1.5):

Let M be an R-module. Then the following statements are equivalent:

(1) M is purely cancellation module.

(2) If AM ⊆ BM, such that A is any ideal of R and B is a pure ideal of R, then A ⊆ B.

(3) If <a>M ⊆ BM, such that a ∈ R and B is a pure ideal of R, then a ∈ B.

(4) (AM:M) = A for all pure ideals A of R.

(5) (AM:BM) = (A:B), for all ideals B of R and for all pure ideals A of R.

Proof: (1) ⇒ (2) suppose that M is purely cancellation module and AM ⊆ BM, where B is a pure ideal of R and A is any ideal of R. Now, BM = AM + BM = (A + B)M, then B = A + B implies A ⊆ B.

(2) ⇒ (3) Let <a>M ⊆ BM. Then <a> ⊆ B by (2). Hence a ∈ B.

(3) ⇒ (4) let x ∈ (AM:M). Then xM ⊆ AM by (3) x ∈ A. Hence (AM:M) ⊆ A.

On the other side if x ∈ A, then xM ⊆ AM. Therefore x ∈ (AM:M) and hence (AM:M) = A.

(4) ⇒ (5) let x ∈ (A:B). Then x ∈ ((AM:M):B) since (AM:M) = A by (4), implies x ∈ (AM:BM) [4,proposition (2.3),p.38].

Now if x ∈ (AM: BM) = ((AM:M):B) and since (AM:M) = A by (4). Then x ∈ (A:B). Therefore (AM:BM) = (A:B).

(5) ⇒ (1) let AM = BM and A is a pure ideal of R, B is any ideal of R. Then (AM:BM) = R implies (A:B) = R. Therefore B ⊆ A.

Similarly A ⊆ B. Then A = B. Hence M is purely cancellation module.

In order to give another characterization of purely cancellation module we need to recall the definition of tensor product of modules and some related lemma: A tensor product of two R-modules A and B means a pair (M,T) where M is an R-module and T: AB → M is a bilinear map, such that for any R-module X and any bilinear map g: AB → X, there exists a unique homeomorphism h: M → X, such that h∘T = g. That is the following diagram is commutative, [3]

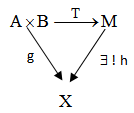The following proposition gives a necessary and sufficient condition for a module to be purely cancellation.

Proposition (1.6):

Let M be an R-module. Then M is purely cancellation module if and only if ann_R(M⊗R) = A for all pure ideals A of R.

Proof: Let M be purely cancellation module. And by [2, proposition (1.11), p.12], we get M⊗R/A ≅ M/AM, where A is pure ideal of R. Therefore ann_R(M⊗R/A) = ann_R(M/AM) = (AM:M) = A by theorem (1.5,(4)).

Now suppose ann_R(M⊗R/A) = A for all pure ideal A of R. M⊗R/A ≅ M/AM by [2, proposition (1.11), p.12]. Then ann_R(M/AM) = ann_R(M⊗R/A) = A. But ann_R(M/AM) = (AM:M). Therefore (AM:M) = A, M is purely cancellation module by theorem (1.5,(4)).

Proposition (1.7):

If M is an R-module and N is a homeomorphic image of M, which is purely cancellation R-module, then M is purely cancellation module.

Proof: Let AM = BM, where A is pure ideal of R and B is any ideal of R. And let θ: M → N be an epimorphism such that N is purely cancellation module. Then θ(AM) = θ(BM). But θ(AM) = Aθ(M) = θ(BM) = Bθ(M). Then AN = BN. But N is purely cancellation R-module. Then A = B which completes the proof.

From proposition (1.7), we get the following result:

Corollary (1.8):

If M has a purely direct summand, then M is also purely cancellation R-module.

The following proposition gives a condition under which the property of purely cancellation and cancellation are equivalents.

Proposition (1.9):

Let M be an R-module. Then M is a cancellation module if and only if M is faithful purely cancellation module.

Proof: It is know that, every cancellation module is purely cancellation module, and every cancellation module is faithful module, [2, remark (1.4), p.8].

Conversely: suppose that M is faithful purely cancellation module. Let AM = BM, where A and B are two ideals in R.

If A is pure ideal of R and B is any ideal of R, implies A = B (since M is purely cancellation module).

If A is not pure ideal of R and B is any ideal of R, AM – BM = 0 ⇒ A – B ⊆ ann(M) = 0. Hence A = B.

Now, we have the following.

Proposition (1.10):

Let M be a cancellation R-module and A be an ideal in R. Then AM is purely cancellation module if and only if A is purely cancellation ideal.

Proof: Suppose that AM is purely cancellation module. To prove that A is purely cancellation ideal. Let BA = CA, where B is a pure ideal of R and C is any ideal of R. Since, BAM = CAM, implies C = B. Therefore A is purely cancellation ideal.

Conversely, suppose that A is purely cancellation ideal and BAM = CAM, where B is pure ideal of R and C is any ideal of R. Then BA = CA (since M is purely cancellation module), implies B = C (since A is purely cancellation ideal). Therefore AM is purely cancellation module.

In the following result and its corollaries we study the relation between purely cancellation module and its trace.

Proposition (1.11):

Let M and N be two R-modules and L = ∑θλ(M) be a submodule of N, where the sum is taken for any subset of Hom(M,N), such that L is purely cancellation module. Then M is purely cancellation module.

Proof: Let AM = BM, where A is a pure ideal of R and B is any ideal of R. Then θλ(AM) = θλ(BM), for each θλ ∈ Hom(M,N), implies . But θλ(AM) = Aθλ(M) = θλ(BM) = B θλ(M). Then 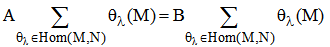. Therefore AL = BL, implies A = B (since L is purely cancellation submodule).

Corollary (1.12):

If M is an R-module and T(M) is purely cancellation ideal of R, then M is purely cancellation module.

Proof: The result is clear by using the definition of T(M) and proposition (1.11).

Corollary (1.13):

If M is an R-module and T(M) is multiplication ideal of R, which contain a non-zero divisor element, then M is purely cancellation module.

Proof: Let a ∈ T(M) and a is a non-zero divisor. T(M) is a multiplication ideal of R, so there exists an ideal J of R, such that: < a > = JT(M). Implies T(M) is an invertable ideal of R [4,proposition (6.3), p.125]. Therefore T(M) is a cancellation ideal [5, p.879]. Implies T(M) is purely cancellation module. Then M is purely cancellation module by corollary (1.12).

Corollary (1.14):

Let M be an R-module, such that T(M) is purely cancellation ideal. Then M* = Hom(M,R) is purely cancellation R-module.

Proof: Let aM* ⊆ BM*, such that B is a pure ideal of R. Now, a f ∈ aM* ⊆ BM*, ∀ f ∈ M*. Thus a f ∈ BM*, implies 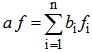, where b_i ∈ B and f_i ∈ M*. Therefore 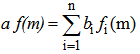, ∀ m ∈ M. Then a T(M) ⊆ B(T(M). But T(M) is purely cancellation ideal. Then a ∈ B by theorem ((1.3), (3)) and hence M* is purely cancellation module.

Recall that a ring R is called regular (Von-Numann) if for each element a ∈ R, there exists an element r ∈ R such that a = a r a (a = a²r if R is commutative), [6].

An R-module M is flat if for each injective homomorphism f: N′ → N from one R-module into another, the homomorphism 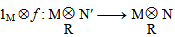is injective, where 1_M is the identity isomorphism of M, [6].

Now, we give the following result.

Proposition (1.15):

Let M be a module over a regular ring R such that AM is faithful for all ideal A of R. Then M is purely cancellation module.

Proof: Let AM = BM, where A is pure ideal of R and B is any ideal of R. From a ring R is regular by [8, proposition (1.10), p.3] we get A²M = B²M. Then A(AM) = B(BM) which implies A(AM) = B(AM ) and hence A – B ⊆ ann(AM) = 0 (since AM is a faithful for all ideal A of R). Thus A = B. Therefore M is purely cancellation module.

As an application of proposition (1.15), we give the following corollary.

Corollary (1.16):

Let M be a flat R-module and AM is faithful for all ideal A of R. hen M is purely cancellation module.

Proof: It is obvious according to [8, proposition (1.12), p.9] and proposition (1.15).

Recall that an R-module M is said to be a multiplication module if for every submodule N of M, there exists an ideal I of R such that N = IM, [6].

Now, we give the following proposition.

Proposition (1.17):

If M is a multiplication R-module. N is purely cancellation submodule, then M is purely cancellation module.

Proof: We have N is a submodule of M and M is multiplication R-module, that is N = JM, where J is an ideal of R. Let AM = BM, where A is pure ideal of R and B is any ideal of R. Then AJM = BJM which implies AN = BN and hence A = B (since N is purely cancellation module). The proof is complete.

Next, we have the following result.

Proposition (1.18):

Let M be a multiplication purely cancellation R-module, N is a submodule of M. Then the following are equivalents:

(1) N is purely cancellation module.

(2) (N:M) is purely cancellation ideal of R.

(3) N = AM, where A is pure ideal of R and satisfies the property of purely cancellation.

Proof: (1) ⇒ (2) Suppose that N is purely cancellation and let A(N:M) = B(N:M), where A is pure ideal of R and B is any ideal of R. Then A(N:M)M = B(N:M)M which implies AN = BN. Hence A = B. Therefore (N:M) is purely cancellation ideal of R.

(2) ⇒ (3) put A = (N:M).

(3) ⇒ (1) Let CN = DN, where C is pure ideal of R and D is any ideal of R. Then CAM = DAM by (3). Thus CA = DA (since M is cancellation module). Therefore C = D by (3). Hence N is purely cancellation module.

A submodule N of an R-module M is said to be pure if IM ∩ N = IN, for every ideal I of R.

In case R is PID or M is cyclic, then N is pure if and only if rM ∩ N = rN, ∀ r ∈ R, [6].

We end this section by the following result.

Proposition (1.19):

Let M be an R-module, N is a pure submodule of M satisfy the property of purely cancellation. Then M is purely cancellation module.

Proof: Let AM = BM, where A is pure ideal of R and B is any ideal of R. We have N is pure submodule, then N ∩ AM = AM and N ∩ BM = BM. Thus AN = BN and hence A = B (since N is purely cancellation module). Therefore M is purely cancellation module.

3. Weak Purely Cancellation Module

As a generalization of purely cancellation property in modules we shall introduce the concept of weak purely cancellation modules. In this section we shall discuss the results that we obtained in section one.

We start with the following definition.

Definition (2.1):

Let M be an R-module. Then M is called weak purely cancellation module if AM = BM, where A is a pure ideal of R and B is any ideal of R, then A + ann(M) = B + ann(M).

Remark (2.2):

Every purely cancellation module is a weak purely cancellation module.

The converse of remark (2.2) is not true, as it is seen by the following example:

Example (2.3):

Consider Z₂ as a Z₄-module and let m₁ = 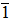∈ Z₄ and m₂ = 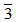∈ Z₄, since m₁ ≠ m₂ and ann(Z₂) = (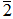). Now, (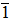) + ann(Z₂) = (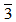) + ann(Z₂) = Z₄. Therefore Z₂ is weak purely cancellation Z₄-module. But Z₂ is not purely cancellation module, see example and remark ((1.2),5).

The converse of remark (2.2) hold under the condition M is faithful.

Proposition (2.4):

If M is a faithful weak purely cancellation module, then M is purely cancellation module.

Proof: Is trivial, so it is omitted.

In the following proposition we shall prove that the class of cyclic modules is contained in the class weak purely cancellation modules.

Proposition (2.5):

Every cyclic module is a weak purely cancellation module.

Proof: Let M = <m> be a cyclic module over R with m ∈ M, and let A<m> = B <m>, where A is a pure ideal in R and B is any ideal in R. Then a m ∈ B<m>, a ∈ A, implies a m = bm, where b ∈ B. Therefore a m – bm = 0, implies (a – b)m = 0. Then a – b ∈ ann(M). But a = b + a – b. Therefore a ∈ B + ann(M), implies A ⊆ B + ann(M).

Then A + ann(M) ⊆ B + ann(M).

Similarly we can prove that B + ann(M) ⊆ A + ann(M) and hence A + ann(M) = B + ann(M), which is what we wanted.

We shall give same characterizations of a weak purely cancellation modules in the following proposition.

Theorem (2.6):

Let M be an R-module. Then the following statements are equivalent:

(1) M is a weak purely cancellation module.

(2) If AM ⊆ BM, such that A is any ideal of R and B is a pure ideal of R then A ⊆ B + ann(M).

(3) If <a>M ⊆ BM, such that a ∈ R and B is a pure ideal of R, then a ∈ B + ann(M).

(4) (AM:M) = A + ann(M), for all pure ideals A of R.

(5) (AM:BM) = (A + ann(M):B), where A is a pure ideal of R and B is any ideal of R.

Proof: It is easy and clear.

Proposition (2.7):

Let M and N be two R-modules and be a submodules of N where the sum is taken for any subset Λ of Hom(M,N), L is weak purely cancellation and ann(L) = ann(M). Then M is a weak purely cancellation module.

Proof: Let AM = BM, where A is pure ideal of R and B is any ideal of R. Then θλ(AM) = θλ(BM), implies 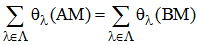. But θλ(AM) = Aθλ(M) = θλ(BM) = Bθλ(M). Then 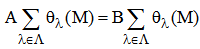. Therefore AL = BL (since L is weak purely cancellation module), implies A +ann(L) = B + ann(L). Therefore A + ann(M) = B + ann(M). Then M is weak purely cancellation module.

Corollary (2.8):

If M is an R-module, T(M) is a weak purely cancellation ideal in R and ann(T(M)) = ann(M). Then M is a weak purelycancellation module.

Proof: The result is clear by using proposition (2.7) and the definition of T(M).

The dual of a module will be weak purely cancellation whenever the trace of the module satisfies this property, as it is shown in the following result.

Proposition (2.9):

If M is an R-module and T(M) is a weak purely cancellation module, and ann(T(M)) = ann(M). Then M is weak purely cancellation module.

Proof: It is obvious.

Proposition (2.10):

If M is a multiplication R-module, N is a submodule of M such that ann_R(N) = ann_R(M) and N is a weak purely cancellation, then M is weak purely cancellation module.

Proof: Let AM = BM, where A is pure ideal of R and B is any ideal of R. Then AIM = BIM (since M is multiplication and I is an ideal of R). Thus AN = BN and hence A + ann(N) = B + ann(N). But ann_R(N) = ann_R(M) which implies A + ann(M) = B + ann(M). Therefore M is purely cancellation module.

Now, we end this section by the following proposition.

Proposition (2.11):

Let M be an R-module, N is pure submodule of M and N is weak purely cancellation such that ann(N) = ann(M). Then M is weak purely cancellation module.