Sevil Bacanli1, Tuğçe Tuncel2
1Hacettepe University, Faculty of Science, Department of Statistics, Beytepe, Ankara, Turkey
2Republic of Turkey Social Security Institution, Ankara, Turkey
Correspondence to: Sevil Bacanli, Hacettepe University, Faculty of Science, Department of Statistics, Beytepe, Ankara, Turkey.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this study, the post-stratified randomized response (RR) models are proposed in order to estimate the proportion of persons bearing the sensitive characteristic. In addition to this, post-stratified RR models are compared according to their efficiencies. It is concluded that Kim-Warde’s post-stratified RR model is more efficient than the Hong et al.’s post-stratified RR model.
Keywords:
Randomized response model, Post-stratified sampling, Stratified random sampling
Cite this paper: Sevil Bacanli, Tuğçe Tuncel, A Post-Stratified Randomized Response Model for Proportion, American Journal of Mathematics and Statistics, Vol. 4 No. 3, 2014, pp. 156-161. doi: 10.5923/j.ajms.20140403.04.
1. Introduction
With the purpose of making people comfortable and encourage them to give truthful answers, a new survey technique was needed to eliminate non-response and response bias and this technique should be different from open and direct surveys. The randomized response technique can be defined as a procedure of collecting the information about sensitive characteristics without revealing the identity of respondent. The first study about randomized response technique was developed by Warner [1] as an alternative way of survey technique and is named as randomized response (RR) model. Warner’s RR model is designed with different features such as estimating the proportion of people who bear a sensitive characteristic, reducing answer bias and keeping the respondents confidentiality. In oder to collect information about a sensitive characteristic, Warner [1] use a randomization device (R). This device could be a deck of cards in which each card has one of the two following two questions:i) Do you have a sensitive characteristic (A) “selected with probability P”ii) Do you have a non-sensitive characteristic (Ac) “ selected with probability(1- P )”.In order to estimate the population proportion 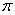 belonging to the sensitive characteristic (A), a simple random sampling with replacement (SRSWR) of n respondents is drawn from the population, and the respondent is required to answer “Yes” or “No” according to her/his actual status and the statement chosen. Hong et. al. [2] proposed a stratified RR model of Warner [1] by using a proportional allocation that applied the same randomization device to each stratum. However, this model may have high expenses, because of the fact that it is difficult to acquire a proportional sample from each stratum. In order to solve this problem, Kim and Warde [3] expanded Hong et al.’s RR model with the optimal allocation and thus, each stratum sample provides different randomization devices. This demonstrated the fact that a stratified RR model with an optimal allocation is more efficient than the one with a proportional allocation. Afterwords, Son et al. [4] proposed the calibration procedure for the variance reduction of the stratified RR models, which are suggested by Hong et al. [2] and Kim and Warde [3], by using auxiliary information at the population level.A part from the Warner’s RR procedure, two-stage RR procedure is proposed by Mangat and Singh [5]. In this procedure, each interviewee with the SRSWR of n respondents is provided with two random devices. Also, Kim and Elam [6] are developed a stratified RR model by using the Mangat and Singh’s RR model.In recent years, various alternative RR models which use two decks of cards are developed. Odumade and Singh [7] proposed the use of two decks of cards in a RR model in which each of the decks included the two statements which are used in Warner’s RR model. Furthermore, Abdelfatah et al. [8] [9] suggested a modified RR model of Odumade and Singh [7] by using Mangat and Singh’s procedure instead of Warner’s procedure in each stage. There after Hong et al. [10] developed an RR model by applying stratified sampling to Abdelfatah et al.’s RR model.Therefore, in literature, RR models have been developed in simple and stratified sampling as the estimator of a sensitive proportion. In this study, the stratified RR models of Warner [1] are examined in post-stratified sampling by using a deck of cards.Post stratified sampling is a very popular method among the survey practitioners and is often used in sample surveys, when the identification of stratum cannot be achieved in advance. In post stratified sampling, first of all, a sample is selected by using simple random, and then, this selected sample is stratified into strata e.g. personal characteristics such as, age, gender, race, occupation, income, educational level and other factors. Therefore, this sampling method is particularly useful in multi-purpose surveys in which stratification factors are selected prior to sampling. [11], [12].This article is organized as follows: In section 2, the stratified RR models of Warner [1] are briefly reviewed. In section 3, post-stratified sampling is described and how post-stratified sampling can be used in RR models are explained and RR models are compared according to their efficiencies. Conclusion is given in section 4.
belonging to the sensitive characteristic (A), a simple random sampling with replacement (SRSWR) of n respondents is drawn from the population, and the respondent is required to answer “Yes” or “No” according to her/his actual status and the statement chosen. Hong et. al. [2] proposed a stratified RR model of Warner [1] by using a proportional allocation that applied the same randomization device to each stratum. However, this model may have high expenses, because of the fact that it is difficult to acquire a proportional sample from each stratum. In order to solve this problem, Kim and Warde [3] expanded Hong et al.’s RR model with the optimal allocation and thus, each stratum sample provides different randomization devices. This demonstrated the fact that a stratified RR model with an optimal allocation is more efficient than the one with a proportional allocation. Afterwords, Son et al. [4] proposed the calibration procedure for the variance reduction of the stratified RR models, which are suggested by Hong et al. [2] and Kim and Warde [3], by using auxiliary information at the population level.A part from the Warner’s RR procedure, two-stage RR procedure is proposed by Mangat and Singh [5]. In this procedure, each interviewee with the SRSWR of n respondents is provided with two random devices. Also, Kim and Elam [6] are developed a stratified RR model by using the Mangat and Singh’s RR model.In recent years, various alternative RR models which use two decks of cards are developed. Odumade and Singh [7] proposed the use of two decks of cards in a RR model in which each of the decks included the two statements which are used in Warner’s RR model. Furthermore, Abdelfatah et al. [8] [9] suggested a modified RR model of Odumade and Singh [7] by using Mangat and Singh’s procedure instead of Warner’s procedure in each stage. There after Hong et al. [10] developed an RR model by applying stratified sampling to Abdelfatah et al.’s RR model.Therefore, in literature, RR models have been developed in simple and stratified sampling as the estimator of a sensitive proportion. In this study, the stratified RR models of Warner [1] are examined in post-stratified sampling by using a deck of cards.Post stratified sampling is a very popular method among the survey practitioners and is often used in sample surveys, when the identification of stratum cannot be achieved in advance. In post stratified sampling, first of all, a sample is selected by using simple random, and then, this selected sample is stratified into strata e.g. personal characteristics such as, age, gender, race, occupation, income, educational level and other factors. Therefore, this sampling method is particularly useful in multi-purpose surveys in which stratification factors are selected prior to sampling. [11], [12].This article is organized as follows: In section 2, the stratified RR models of Warner [1] are briefly reviewed. In section 3, post-stratified sampling is described and how post-stratified sampling can be used in RR models are explained and RR models are compared according to their efficiencies. Conclusion is given in section 4.
2. Stratified Randomized Response Model
Let us consider a stratified random sampling with L strata. For each strata size (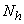 ),
),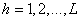 and then, a sample (
and then, a sample (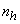 ) is selected with simple random sampling for each stratum. The number of units in each stratum is assumed to be known. Hong et al. [2] suggested a stratified RR model which applies the same randomization device to every stratum.Each respondent in the sample stratum (
) is selected with simple random sampling for each stratum. The number of units in each stratum is assumed to be known. Hong et al. [2] suggested a stratified RR model which applies the same randomization device to every stratum.Each respondent in the sample stratum (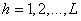 ) is provided with the randomization device
) is provided with the randomization device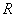 which includes a sensitive characteristic (
which includes a sensitive characteristic (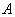 ) card with probability
) card with probability 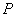 and its non-sensitive characteristic (
and its non-sensitive characteristic (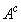 ) card with probability
) card with probability 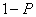 . The respondent is required to answer the question with “Yes” or “No” but s/he should not report the question card that she or he has. A respondent who is a part of the sample in different strata will perform the same randomization devices. Let
. The respondent is required to answer the question with “Yes” or “No” but s/he should not report the question card that she or he has. A respondent who is a part of the sample in different strata will perform the same randomization devices. Let 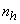 be the number of units in the sample from stratum
be the number of units in the sample from stratum 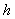 , and then,
, and then, 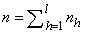 is the total number of units in the sample from all strata. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the
is the total number of units in the sample from all strata. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the 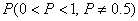 , the proportion of a “Yes” answer in stratum
, the proportion of a “Yes” answer in stratum 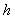 for this procedure is
for this procedure is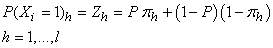 | (1) |
where 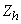 is the proportion of “yes” answer in stratum
is the proportion of “yes” answer in stratum  ,
, 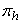 is the proportion of respondents with sensitive characteristic in stratum
is the proportion of respondents with sensitive characteristic in stratum 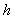 and
and 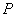 is the probability in a respondent’s sensitive characteristic (
is the probability in a respondent’s sensitive characteristic (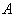 ) card. The maximum likelihood estimator (MLE) of
) card. The maximum likelihood estimator (MLE) of 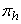 is
is 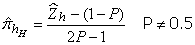 | (2) |
where the proportion of “Yes” answer in a sample of the stratum  is
is  . The variance of
. The variance of  can be given as
can be given as 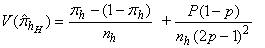 | (3) |
Considering each 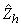 is distributed with
is distributed with 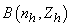 and selections in different strata are made independently, the estimate of is
and selections in different strata are made independently, the estimate of is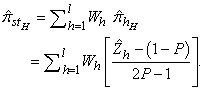 | (4) |
The variance of 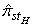 can be given as
can be given as 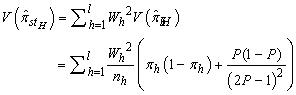 | (5) |
[2]. Kim and Warde [3] introduced a different estimator from Hong et al’s estimator for stratified random sampling. According to Kim and Warde [3], it is considered that each respondent in the sample stratum 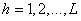 is provided with the randomization device
is provided with the randomization device 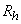 and this device contains a sensitive characteristic (
and this device contains a sensitive characteristic (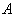 ) card with probability
) card with probability 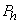 and its negative question (
and its negative question (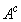 ) card with probability
) card with probability 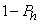 . The respondent is supposed to answer the question with “Yes” or “No” but s/he should not report the question card that he or she has. A respondent is a member of the sample in a different strata will perform different randomization devices and each of those devices has different preassigned probabilities. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the
. The respondent is supposed to answer the question with “Yes” or “No” but s/he should not report the question card that he or she has. A respondent is a member of the sample in a different strata will perform different randomization devices and each of those devices has different preassigned probabilities. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the 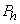
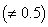 , the proportion of a “Yes” answer in stratum h for this procedure is:
, the proportion of a “Yes” answer in stratum h for this procedure is: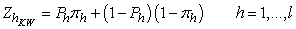 | (6) |
where 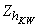 is the proportion of “Yes” answer in stratum
is the proportion of “Yes” answer in stratum 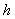 , the proportion of respondents with a sensitive characteristic in stratum h is and, at the same time, is the probability of a sensitive question (
, the proportion of respondents with a sensitive characteristic in stratum h is and, at the same time, is the probability of a sensitive question (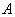 ) card of a respondent in the sample stratum
) card of a respondent in the sample stratum 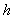 . The maximum likelihood estimator (MLE) of is
. The maximum likelihood estimator (MLE) of is 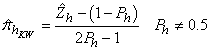 | (7) |
where 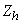 is the proportion of “Yes” answer in a sample of the stratum
is the proportion of “Yes” answer in a sample of the stratum 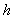 . The variance of
. The variance of 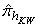 is given by
is given by 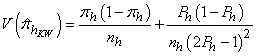 | (8) |
[4]. Considering the fact that is a binomial distribution and selections in different strata are made independently, the MLE estimate 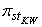 of a sensitive proportion can be given as
of a sensitive proportion can be given as 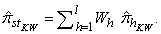 | (9) |
The variance of 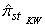 is
is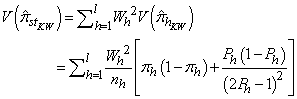 | (10) |
[3], [4].
3. Post-Stratified Randomized Response Model
In a post-stratified sampling, firstly, a sample of n units is selected from the population of 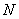 units by using simple random sampling. The population is stratified into
units by using simple random sampling. The population is stratified into 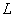 strata on the basis of some known auxiliary information. In post stratified sampling, the values of
strata on the basis of some known auxiliary information. In post stratified sampling, the values of 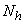 , where
, where 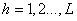 and may or may not be known for each sample unit which is selected with the chosen design. After that, each sample unit which are post-stratified or placed in the
and may or may not be known for each sample unit which is selected with the chosen design. After that, each sample unit which are post-stratified or placed in the 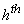 stratum based on the auxiliary information is associated as such
stratum based on the auxiliary information is associated as such 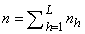 . Thus the difference between stratified and post-stratified sampling schemes is that the sub-sample size
. Thus the difference between stratified and post-stratified sampling schemes is that the sub-sample size 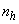 is a fixed or predefined number in stratified sampling, whereas it is a random variable in post-stratified sampling [12].As for the proportion in the population, the appropriate estimate for post-stratified sampling is
is a fixed or predefined number in stratified sampling, whereas it is a random variable in post-stratified sampling [12].As for the proportion in the population, the appropriate estimate for post-stratified sampling is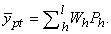 | (11) |
In post-stratified sampling, the variance of 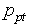 is
is 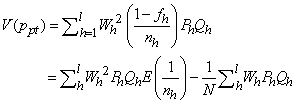 | (12) |
[13]. In this situation, a general expression for 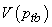 can be approximated by replacing
can be approximated by replacing 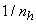 with its expected value. It is difficult to find the expected value of the reciprocal of a random variable; thus, a good approximation can be given as
with its expected value. It is difficult to find the expected value of the reciprocal of a random variable; thus, a good approximation can be given as 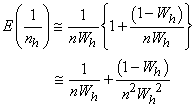 | (13) |
[14]. By replacing this with 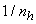 for variance of the mean estimator in equation, the variance of the post-stratified proportion estimator can be given as
for variance of the mean estimator in equation, the variance of the post-stratified proportion estimator can be given as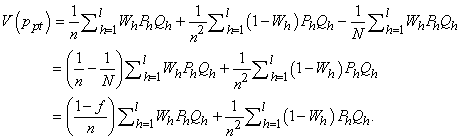 | (14) |
If 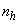 were fixed, post-stratification of proportion estimator and variance would function as the proportion estimation in the stratified random sampling under proportional allocation [12]. Therefore, in accordance with this information, RR estimators of a sensitive proportion for post-stratified sampling which is given section 2 are demonstrated as below:The Hong K. et al. RR estimator for post-stratified sampling can be given as
were fixed, post-stratification of proportion estimator and variance would function as the proportion estimation in the stratified random sampling under proportional allocation [12]. Therefore, in accordance with this information, RR estimators of a sensitive proportion for post-stratified sampling which is given section 2 are demonstrated as below:The Hong K. et al. RR estimator for post-stratified sampling can be given as 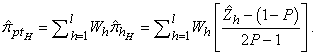 | (15) |
Subsituting (13) into (5), variance of this estimator can be obtained as such; 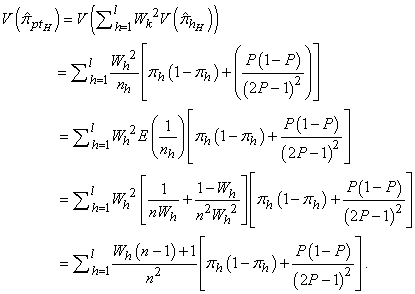 | (16) |
Similarly, Kim-Warde’s RR estimator for post stratified sampling can be defined as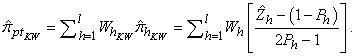 | (17) |
In order to obtain the variance of this estimator, (13) is subsituted into (10) as follows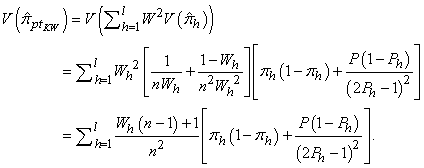 | (18) |
Therefore, post-stratified RR- estimators are same as stratified RR-estimators. But the variance equations are different in post-stratified sampling.
3.1. Efficiency Comparison
In this section, a comparison of the relative efficiency (RE) is carried out in post-stratified RR models. Kim and Warde [3] resorted to an empirical study on RE for stratified random sampling and it is seen that Kim and Warde’s stratified RR model is more efficient than Hong et al.’s- stratified RR model. Similar efficiency comparison is carried out for post-stratified sampling.Let us assume that there are two strata in a population in which it is considered that 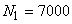 ,
, 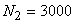 and selection probabilities of sensitive question are
and selection probabilities of sensitive question are 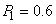 to
to 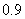 by increments for stratum
by increments for stratum 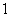 and
and 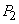 is different from
is different from  . The RE of two variances in post-stratification is
. The RE of two variances in post-stratification is 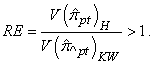 | (19) |
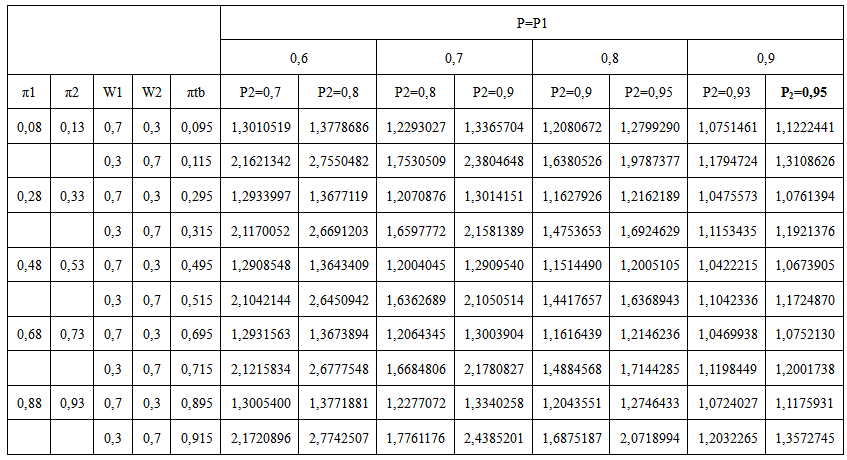 | Table 1. The relative efficiency of post-stratified 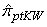 with respect to with respect to 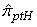 |
Since the value of the RE is higher than one, Kim and Warde’s post- stratified RR model is more efficient than the Hong et al.’s post- stratified RR model for all 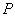 . Table 1 shows that the values of the relative efficiency are higher than one for all parameter values tabled. Therefore, Kim and Warde’s RR model is more efficient in both sampling methods; stratified and post-stratified.In terms of relative efficiency, the results obtained from stratified sampling are similar to the results obtained from post-stratification sampling. However, usage advantages for post-stratification sampling are applied to RR models.
. Table 1 shows that the values of the relative efficiency are higher than one for all parameter values tabled. Therefore, Kim and Warde’s RR model is more efficient in both sampling methods; stratified and post-stratified.In terms of relative efficiency, the results obtained from stratified sampling are similar to the results obtained from post-stratification sampling. However, usage advantages for post-stratification sampling are applied to RR models.
4. Conclusions
RR models are methods for eliminating response bias by keeping the respondent’s confidentiality in surveys with a sensitive characteristic such as domestic violence, drug use, sexual behaviour, family income, tax evasion etc. In this study, Warner’s RR models in stratified sampling are extended into post- stratified sampling by using a deck of cards. Warner’s RR models are proposed for post-stratified sampling which is more advantageous in application and it is concluded that Kim & Warde’s RR model is more efficient.In forthcoming studies, we hope to examine the use of two decks of cards in a RR model for post-stratified sampling.
References
| [1] | Warner, S.L., 1965, Randomized Response: A survey technique for eliminating evasive answer bias. Journal of the American Statistical Association. 60,63-69. |
| [2] | Hong, K., Yum, J., Lee, H., 1994, A stratified randomized response technique. The Korean Journal of Applied Statistics 7, 141-147. |
| [3] | Kim, J., Warde, W.D., 2004, A stratified Warner’s randomized response model. Journal of Statistical Planning and Inference. 120, 155-165. |
| [4] | Son, C., Hong, K., Lee, G., Kim, J., 2008, The Calibration for Stratified Randomized Response Estimators. Communications of the Korean Statistical Society Vol.15, No. 4, pp. |
| [5] | Mangat, N.S, Singh, R., 1990, An alternative randomized response procedure. Biometrika 77: 439-442 |
| [6] | Kim, J., Elam, M., 2005, A two-stage stratified Warner’s randomized response model using optimal allocation. Metrika 61, 1-7. |
| [7] | Odumade, O., Singh, S., 2009, Efficient Use of Two Decks of Cards in Randomized Response Sampling. Communication in Statistics- Theory and Methods, 38,439-446. |
| [8] | Abdelfatah,S., Mazloum, R., Singh, S., 2011, An alternative Randomized Response model Using Two Decks of Cards. Statistica, 3,381-390. |
| [9] | Abdelfatah,S., Mazloum, R., Singh, S., 2013, Efficient Use of a Two-Stage Randomized Response Procedure. Brazilian Journal of Probability and Statistics, 27,4, 608-617. |
| [10] | Hong, K., Lee, G., Son, C., Kim, J., 2014, An Estimation of a Sensitive Attribute by Two Stage Stratified Randomized Response Model. Model Assisted Statistics and Applications 9, 25-35. |
| [11] | Holt, D., Smith, T.M.F., 1979, Post-Stratification. Journal of the Royal Statistical Society A. 142, 33- 46. |
| [12] | Singh, S., 2003, Advanced Sampling Theory with Applications: How Micheal Selected Amy, Volume II, Kluwer Academic Publisher, ISBN Vol. 2:1-4020-1707-3The Netherlands, 889p. |
| [13] | Cochran, W.G., 1977, Sampling techniques. 3rd edn New York: John Wiley and sons. |
| [14] | Hansen, M.H., Hurwitz, W.N., Madow W.G., 1953, Sample Survey Methods and Theory Volume II-Theory. Canada; John Wiley & Sons, Incorporation. |
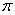 belonging to the sensitive characteristic (A), a simple random sampling with replacement (SRSWR) of n respondents is drawn from the population, and the respondent is required to answer “Yes” or “No” according to her/his actual status and the statement chosen. Hong et. al. [2] proposed a stratified RR model of Warner [1] by using a proportional allocation that applied the same randomization device to each stratum. However, this model may have high expenses, because of the fact that it is difficult to acquire a proportional sample from each stratum. In order to solve this problem, Kim and Warde [3] expanded Hong et al.’s RR model with the optimal allocation and thus, each stratum sample provides different randomization devices. This demonstrated the fact that a stratified RR model with an optimal allocation is more efficient than the one with a proportional allocation. Afterwords, Son et al. [4] proposed the calibration procedure for the variance reduction of the stratified RR models, which are suggested by Hong et al. [2] and Kim and Warde [3], by using auxiliary information at the population level.A part from the Warner’s RR procedure, two-stage RR procedure is proposed by Mangat and Singh [5]. In this procedure, each interviewee with the SRSWR of n respondents is provided with two random devices. Also, Kim and Elam [6] are developed a stratified RR model by using the Mangat and Singh’s RR model.In recent years, various alternative RR models which use two decks of cards are developed. Odumade and Singh [7] proposed the use of two decks of cards in a RR model in which each of the decks included the two statements which are used in Warner’s RR model. Furthermore, Abdelfatah et al. [8] [9] suggested a modified RR model of Odumade and Singh [7] by using Mangat and Singh’s procedure instead of Warner’s procedure in each stage. There after Hong et al. [10] developed an RR model by applying stratified sampling to Abdelfatah et al.’s RR model.Therefore, in literature, RR models have been developed in simple and stratified sampling as the estimator of a sensitive proportion. In this study, the stratified RR models of Warner [1] are examined in post-stratified sampling by using a deck of cards.Post stratified sampling is a very popular method among the survey practitioners and is often used in sample surveys, when the identification of stratum cannot be achieved in advance. In post stratified sampling, first of all, a sample is selected by using simple random, and then, this selected sample is stratified into strata e.g. personal characteristics such as, age, gender, race, occupation, income, educational level and other factors. Therefore, this sampling method is particularly useful in multi-purpose surveys in which stratification factors are selected prior to sampling. [11], [12].This article is organized as follows: In section 2, the stratified RR models of Warner [1] are briefly reviewed. In section 3, post-stratified sampling is described and how post-stratified sampling can be used in RR models are explained and RR models are compared according to their efficiencies. Conclusion is given in section 4.
belonging to the sensitive characteristic (A), a simple random sampling with replacement (SRSWR) of n respondents is drawn from the population, and the respondent is required to answer “Yes” or “No” according to her/his actual status and the statement chosen. Hong et. al. [2] proposed a stratified RR model of Warner [1] by using a proportional allocation that applied the same randomization device to each stratum. However, this model may have high expenses, because of the fact that it is difficult to acquire a proportional sample from each stratum. In order to solve this problem, Kim and Warde [3] expanded Hong et al.’s RR model with the optimal allocation and thus, each stratum sample provides different randomization devices. This demonstrated the fact that a stratified RR model with an optimal allocation is more efficient than the one with a proportional allocation. Afterwords, Son et al. [4] proposed the calibration procedure for the variance reduction of the stratified RR models, which are suggested by Hong et al. [2] and Kim and Warde [3], by using auxiliary information at the population level.A part from the Warner’s RR procedure, two-stage RR procedure is proposed by Mangat and Singh [5]. In this procedure, each interviewee with the SRSWR of n respondents is provided with two random devices. Also, Kim and Elam [6] are developed a stratified RR model by using the Mangat and Singh’s RR model.In recent years, various alternative RR models which use two decks of cards are developed. Odumade and Singh [7] proposed the use of two decks of cards in a RR model in which each of the decks included the two statements which are used in Warner’s RR model. Furthermore, Abdelfatah et al. [8] [9] suggested a modified RR model of Odumade and Singh [7] by using Mangat and Singh’s procedure instead of Warner’s procedure in each stage. There after Hong et al. [10] developed an RR model by applying stratified sampling to Abdelfatah et al.’s RR model.Therefore, in literature, RR models have been developed in simple and stratified sampling as the estimator of a sensitive proportion. In this study, the stratified RR models of Warner [1] are examined in post-stratified sampling by using a deck of cards.Post stratified sampling is a very popular method among the survey practitioners and is often used in sample surveys, when the identification of stratum cannot be achieved in advance. In post stratified sampling, first of all, a sample is selected by using simple random, and then, this selected sample is stratified into strata e.g. personal characteristics such as, age, gender, race, occupation, income, educational level and other factors. Therefore, this sampling method is particularly useful in multi-purpose surveys in which stratification factors are selected prior to sampling. [11], [12].This article is organized as follows: In section 2, the stratified RR models of Warner [1] are briefly reviewed. In section 3, post-stratified sampling is described and how post-stratified sampling can be used in RR models are explained and RR models are compared according to their efficiencies. Conclusion is given in section 4. 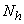 ),
),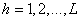 and then, a sample (
and then, a sample (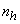 ) is selected with simple random sampling for each stratum. The number of units in each stratum is assumed to be known. Hong et al. [2] suggested a stratified RR model which applies the same randomization device to every stratum.Each respondent in the sample stratum (
) is selected with simple random sampling for each stratum. The number of units in each stratum is assumed to be known. Hong et al. [2] suggested a stratified RR model which applies the same randomization device to every stratum.Each respondent in the sample stratum (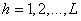 ) is provided with the randomization device
) is provided with the randomization device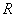 which includes a sensitive characteristic (
which includes a sensitive characteristic (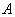 ) card with probability
) card with probability 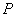 and its non-sensitive characteristic (
and its non-sensitive characteristic (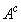 ) card with probability
) card with probability 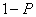 . The respondent is required to answer the question with “Yes” or “No” but s/he should not report the question card that she or he has. A respondent who is a part of the sample in different strata will perform the same randomization devices. Let
. The respondent is required to answer the question with “Yes” or “No” but s/he should not report the question card that she or he has. A respondent who is a part of the sample in different strata will perform the same randomization devices. Let 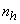 be the number of units in the sample from stratum
be the number of units in the sample from stratum 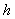 , and then,
, and then, 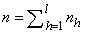 is the total number of units in the sample from all strata. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the
is the total number of units in the sample from all strata. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the 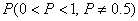 , the proportion of a “Yes” answer in stratum
, the proportion of a “Yes” answer in stratum 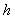 for this procedure is
for this procedure is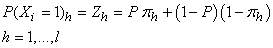
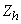 is the proportion of “yes” answer in stratum
is the proportion of “yes” answer in stratum 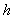 ,
, 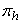 is the proportion of respondents with sensitive characteristic in stratum
is the proportion of respondents with sensitive characteristic in stratum 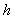 and
and 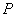 is the probability in a respondent’s sensitive characteristic (
is the probability in a respondent’s sensitive characteristic (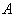 ) card. The maximum likelihood estimator (MLE) of
) card. The maximum likelihood estimator (MLE) of 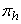 is
is 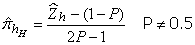
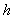 is
is 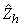 . The variance of
. The variance of 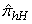 can be given as
can be given as 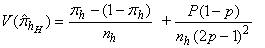
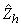 is distributed with
is distributed with 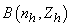 and selections in different strata are made independently, the estimate of is
and selections in different strata are made independently, the estimate of is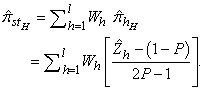
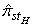 can be given as
can be given as 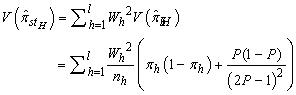
 is provided with the randomization device
is provided with the randomization device  and this device contains a sensitive characteristic (
and this device contains a sensitive characteristic ( ) card with probability
) card with probability 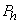 and its negative question (
and its negative question (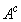 ) card with probability
) card with probability 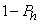 . The respondent is supposed to answer the question with “Yes” or “No” but s/he should not report the question card that he or she has. A respondent is a member of the sample in a different strata will perform different randomization devices and each of those devices has different preassigned probabilities. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the
. The respondent is supposed to answer the question with “Yes” or “No” but s/he should not report the question card that he or she has. A respondent is a member of the sample in a different strata will perform different randomization devices and each of those devices has different preassigned probabilities. Assuming that the “Yes” or “No” reports are made truthfully and the researcher set the 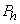
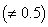 , the proportion of a “Yes” answer in stratum h for this procedure is:
, the proportion of a “Yes” answer in stratum h for this procedure is: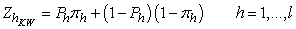
 is the proportion of “Yes” answer in stratum
is the proportion of “Yes” answer in stratum  , the proportion of respondents with a sensitive characteristic in stratum h is and, at the same time, is the probability of a sensitive question (
, the proportion of respondents with a sensitive characteristic in stratum h is and, at the same time, is the probability of a sensitive question (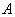 ) card of a respondent in the sample stratum
) card of a respondent in the sample stratum 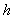 . The maximum likelihood estimator (MLE) of is
. The maximum likelihood estimator (MLE) of is 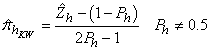
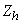 is the proportion of “Yes” answer in a sample of the stratum
is the proportion of “Yes” answer in a sample of the stratum 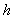 . The variance of
. The variance of 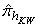 is given by
is given by 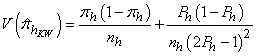
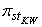 of a sensitive proportion can be given as
of a sensitive proportion can be given as 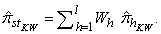
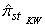 is
is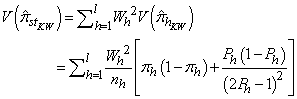
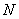 units by using simple random sampling. The population is stratified into
units by using simple random sampling. The population is stratified into 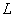 strata on the basis of some known auxiliary information. In post stratified sampling, the values of
strata on the basis of some known auxiliary information. In post stratified sampling, the values of 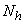 , where
, where 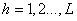 and may or may not be known for each sample unit which is selected with the chosen design. After that, each sample unit which are post-stratified or placed in the
and may or may not be known for each sample unit which is selected with the chosen design. After that, each sample unit which are post-stratified or placed in the 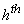 stratum based on the auxiliary information is associated as such
stratum based on the auxiliary information is associated as such 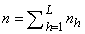 . Thus the difference between stratified and post-stratified sampling schemes is that the sub-sample size
. Thus the difference between stratified and post-stratified sampling schemes is that the sub-sample size 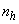 is a fixed or predefined number in stratified sampling, whereas it is a random variable in post-stratified sampling [12].As for the proportion in the population, the appropriate estimate for post-stratified sampling is
is a fixed or predefined number in stratified sampling, whereas it is a random variable in post-stratified sampling [12].As for the proportion in the population, the appropriate estimate for post-stratified sampling is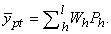
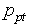 is
is 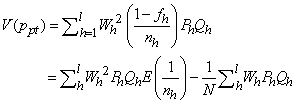
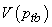 can be approximated by replacing
can be approximated by replacing 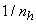 with its expected value. It is difficult to find the expected value of the reciprocal of a random variable; thus, a good approximation can be given as
with its expected value. It is difficult to find the expected value of the reciprocal of a random variable; thus, a good approximation can be given as 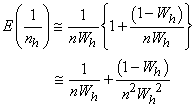
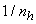 for variance of the mean estimator in equation, the variance of the post-stratified proportion estimator can be given as
for variance of the mean estimator in equation, the variance of the post-stratified proportion estimator can be given as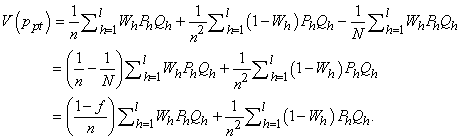
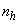 were fixed, post-stratification of proportion estimator and variance would function as the proportion estimation in the stratified random sampling under proportional allocation [12]. Therefore, in accordance with this information, RR estimators of a sensitive proportion for post-stratified sampling which is given section 2 are demonstrated as below:The Hong K. et al. RR estimator for post-stratified sampling can be given as
were fixed, post-stratification of proportion estimator and variance would function as the proportion estimation in the stratified random sampling under proportional allocation [12]. Therefore, in accordance with this information, RR estimators of a sensitive proportion for post-stratified sampling which is given section 2 are demonstrated as below:The Hong K. et al. RR estimator for post-stratified sampling can be given as 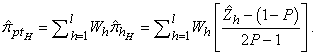
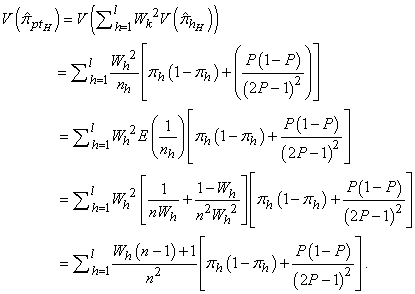
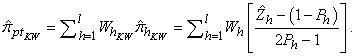
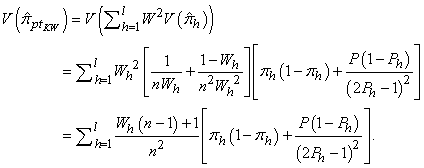
 ,
, 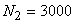 and selection probabilities of sensitive question are
and selection probabilities of sensitive question are 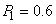 to
to 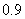 by increments for stratum
by increments for stratum 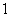 and
and 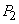 is different from
is different from  . The RE of two variances in post-stratification is
. The RE of two variances in post-stratification is 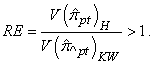

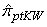 with respect to
with respect to 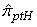
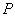 . Table 1 shows that the values of the relative efficiency are higher than one for all parameter values tabled. Therefore, Kim and Warde’s RR model is more efficient in both sampling methods; stratified and post-stratified.In terms of relative efficiency, the results obtained from stratified sampling are similar to the results obtained from post-stratification sampling. However, usage advantages for post-stratification sampling are applied to RR models.
. Table 1 shows that the values of the relative efficiency are higher than one for all parameter values tabled. Therefore, Kim and Warde’s RR model is more efficient in both sampling methods; stratified and post-stratified.In terms of relative efficiency, the results obtained from stratified sampling are similar to the results obtained from post-stratification sampling. However, usage advantages for post-stratification sampling are applied to RR models. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML