Waggas Galib Atshan1, Ali Hussein Battor2, Amal Mohammed Dereush2
1Department of Mathematics, College of Computer Science and Mathematics, University of Al-Qadisiya, Diwaniya, Iraq
2Department of Mathematics, College of Education for Girls, University of Kufa, Najaf, Iraq
Correspondence to: Waggas Galib Atshan, Department of Mathematics, College of Computer Science and Mathematics, University of Al-Qadisiya, Diwaniya, Iraq.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we have introduced and studied a new class of multivalent functions in the open unit disk 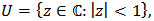 we obtain some interesting properties, like, coefficient inequality, distortion bounds, closure theorems, radii of starlikeness, convexity and close-to-convexity, weighted mean, neighborhoods and partial sums.
we obtain some interesting properties, like, coefficient inequality, distortion bounds, closure theorems, radii of starlikeness, convexity and close-to-convexity, weighted mean, neighborhoods and partial sums.
Keywords:
Multivalent Function, Convolution, Distortion, Neighborhoods, Partial Sums, Weighted Mean, Linear Operator
Cite this paper: Waggas Galib Atshan, Ali Hussein Battor, Amal Mohammed Dereush, On a New Class of Multivalent Functions with Negative Coefficient Defined by Hadamard Product Involving a Linear Operator, American Journal of Mathematics and Statistics, Vol. 4 No. 3, 2014, pp. 147-155. doi: 10.5923/j.ajms.20140403.03.
1. Introduction
Let 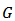 denote the class of all functions of the from
denote the class of all functions of the from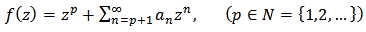 | (1) |
which are analytic and multivalent in the open unit disk 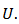 Let
Let 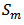 denote the subclass of
denote the subclass of 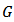 consisting of functions of the from
consisting of functions of the from 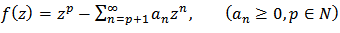 | (2) |
which are analytic and multivalent in the open unit disk 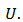 For the function
For the function 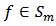 given by (2) and
given by (2) and 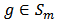 defined by
defined by 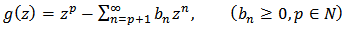 | (3) |
we define the convolution (or Hadamard product) of 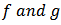 by
by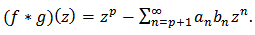 | (4) |
A function 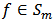 is said to be p-valentlystarlike of order
is said to be p-valentlystarlike of order 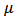 if and only if
if and only if 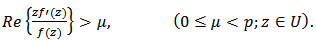 | (5) |
A function 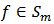 is said to be p-valently convex of order
is said to be p-valently convex of order 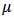 if and only if
if and only if | (6) |
A function 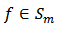 is said to be p-valently close-to-convex of order
is said to be p-valently close-to-convex of order 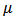 if and only if
if and only if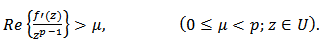 | (7) |
Definition 1 [8]: Let 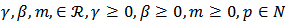 and
and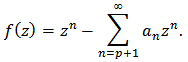 Then we define the linear operator
Then we define the linear operator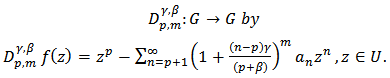 | (8) |
Definition 2: Let 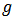 be a fixed function defined by (3). The function
be a fixed function defined by (3). The function 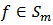 given by (2) is said to be in the class
given by (2) is said to be in the class 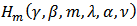 if and only if
if and only if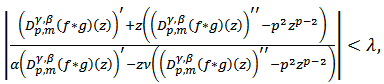 | (9) |
where 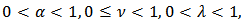
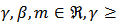
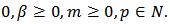 Some of the following properties studied for other class in [1], [2], [3], [4], [6] and [7].
Some of the following properties studied for other class in [1], [2], [3], [4], [6] and [7].
2. Coefficient Inequalities
Theorem 1: Let 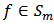 . Then
. Then 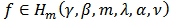 if and only if
if and only if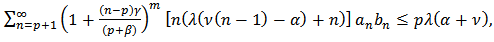 | (10) |
where 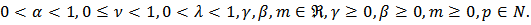 The result is sharp for the function
The result is sharp for the function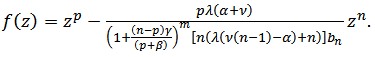 | (11) |
Proof: Suppose that the inequality (10) holds true and 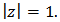 Then we have
Then we have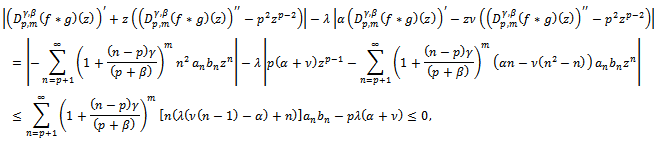 by hypothesis.Hence, by maximum modulus principle,
by hypothesis.Hence, by maximum modulus principle, 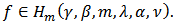 Conversely, suppose that
Conversely, suppose that 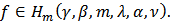 Then from (9), we have
Then from (9), we have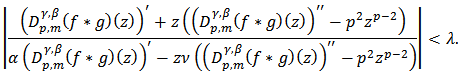 Since
Since 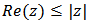 for all
for all  we get
we get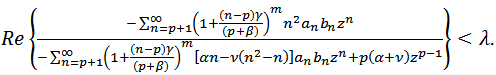 | (12) |
We choose the value of 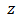 on the real axis, so that
on the real axis, so that 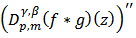 is real.Letting
is real.Letting 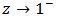 through real values, we obtain inequality (10).Finally, sharpness follows if we take
through real values, we obtain inequality (10).Finally, sharpness follows if we take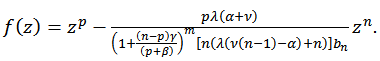 | (13) |
Corollary 1: Let 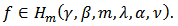 Then
Then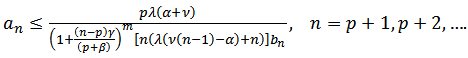 | (14) |
3. Growth and Distortion Theorems
Theorem 2: Let the function 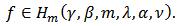 Then
Then 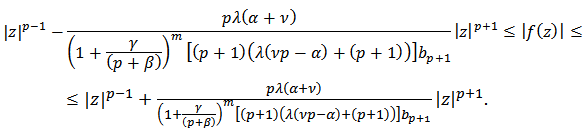 | (15) |
Proof: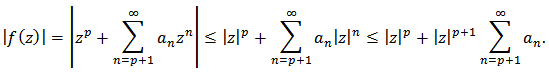 By Theorem 1, we get
By Theorem 1, we get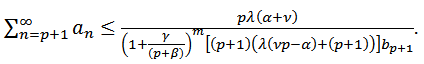 | (16) |
Thus 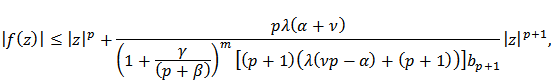 also
also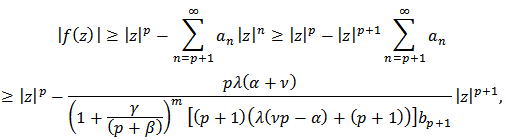 and the proof is complete.Theorem 3: Let
and the proof is complete.Theorem 3: Let 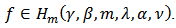 Then
Then 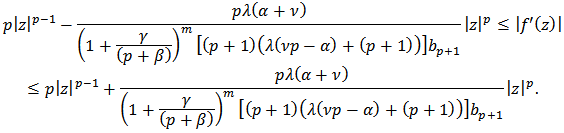 Proof: Notice that
Proof: Notice that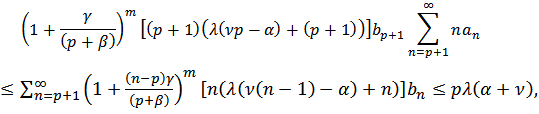 | (17) |
from Theorem 1, thus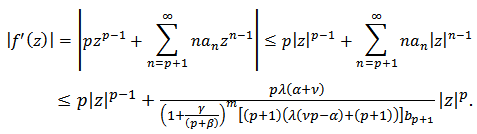 | (18) |
On the other hand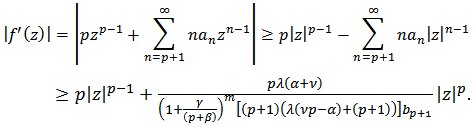 | (19) |
Combining (18) and (19), we get the result.Closure Theorems:Theorem 4: Let the function 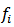 defined by
defined by | (20) |
be in the class 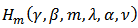 for every
for every 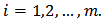 Then the function
Then the function 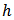 defined by
defined by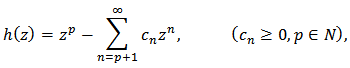 also belongs to the class
also belongs to the class 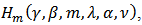 where
where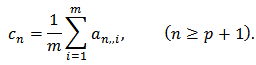 Proof: Since
Proof: Since 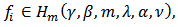 then by Theorem 1, we have
then by Theorem 1, we have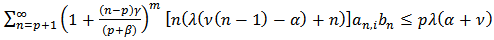 | (21) |
for every 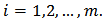 Hence
Hence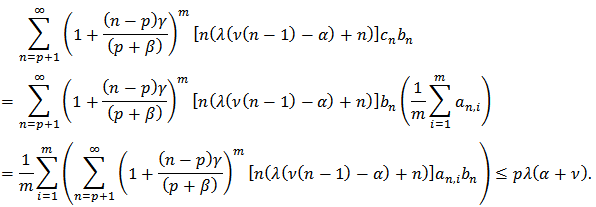 By Theorem 1, it follows that
By Theorem 1, it follows that 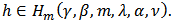 Theorem 5: Let the function
Theorem 5: Let the function 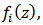 defined by (20) be in the class
defined by (20) be in the class 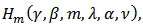 for every
for every 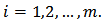 Then the function
Then the function 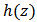 defined by
defined by 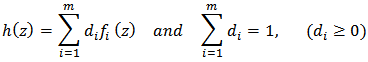 is also in the class
is also in the class 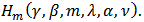 Proof: By definition of
Proof: By definition of 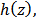 we have
we have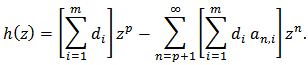 Since
Since 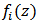 are in the class
are in the class 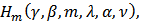 for every
for every 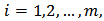 we obtain
we obtain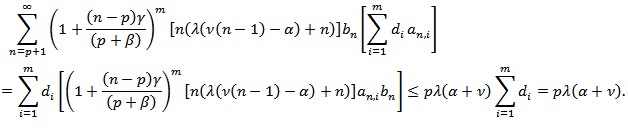
4. Radii of Starlikeness, Convexity and Close-to-Convexity
In the following theorems, we obtain the radii of starlikeness, convexity and close-to-convexity for the class 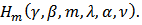 Theorem 6: If
Theorem 6: If 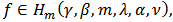 then
then 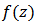 is p-valentlystarlike of order
is p-valentlystarlike of order 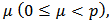 in the dick
in the dick 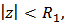 where
where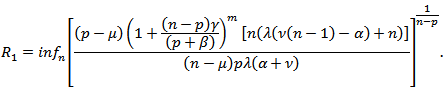 Proof: It is sufficient to show that
Proof: It is sufficient to show that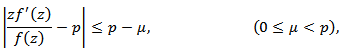 for
for 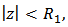 we have
we have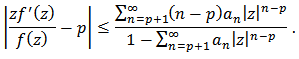 Thus
Thus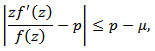 if
if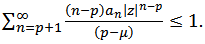 | (22) |
Hence, by Theorem 1, (22) will be true if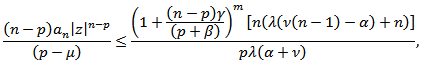 or if
or if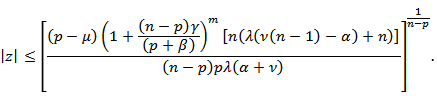 Setting
Setting 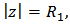 we get the desired result.Theorem 7: If
we get the desired result.Theorem 7: If 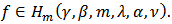 Then
Then 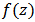 is p-valently convex of order
is p-valently convex of order 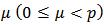 in the disk
in the disk 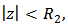 where
where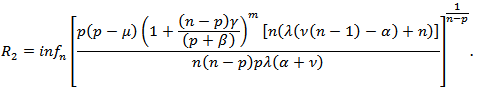 Proof: It is sufficient to show that
Proof: It is sufficient to show that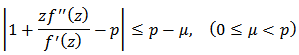 for
for 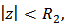 we have
we have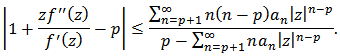 Thus
Thus 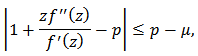 if
if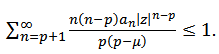 | (23) |
Hence by Theorem 1, (23) will be true if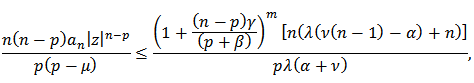 and hence
and hence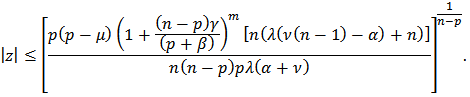 Setting
Setting 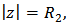 we get the desired result.Theorem 8: Let the function
we get the desired result.Theorem 8: Let the function 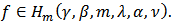 Then
Then 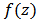 is p-valently close-to-convex of order
is p-valently close-to-convex of order 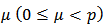 in the disk
in the disk 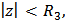 where
where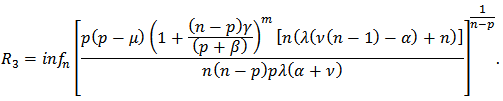 Proof: It is sufficient to show that
Proof: It is sufficient to show that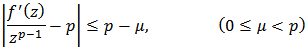 for
for 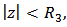 we have
we have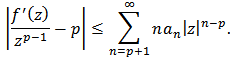 Thus
Thus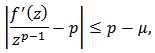 if
if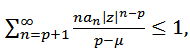 | (24) |
hence, by Theorem 1, (24) will be true if 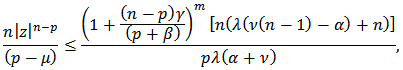 and hence
and hence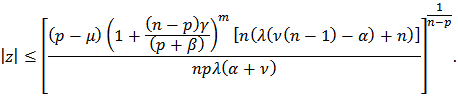 Setting
Setting 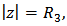 we get the desired result.
we get the desired result.
5. Weighted Mean
Definition 3: Let 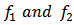 be in the class
be in the class 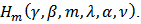 Then the weighted mean
Then the weighted mean 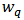 of
of 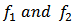 is given by
is given by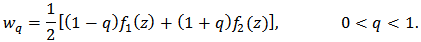 Theorem 9: Let
Theorem 9: Let 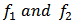 be in the class
be in the class 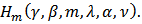 Then the weighted mean
Then the weighted mean 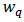 of
of 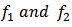 is also in the class
is also in the class 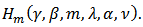 Poof: By Definition 3, we have
Poof: By Definition 3, we have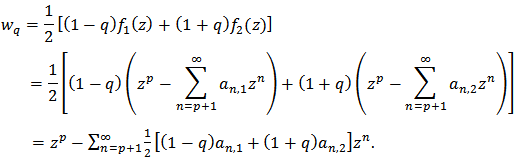 | (25) |
Since 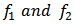 are in the class
are in the class 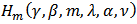 so by Theorem 1, we get
so by Theorem 1, we get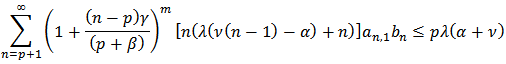 and
and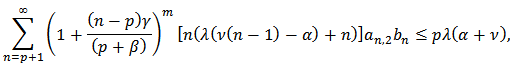 Hence
Hence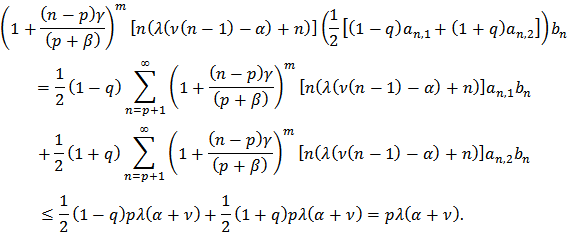 Therefore
Therefore 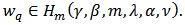 The proof is complete.
The proof is complete.
6. Neighborhoods and Partial Sums
Now we define the 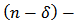 neighborhoods of the function
neighborhoods of the function  by
by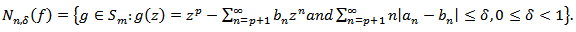 | (26) |
For identity function 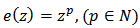
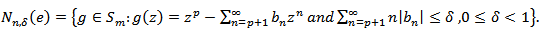 | (27) |
The concept of neighborhoods was first introduced by Goodman [5] and then generalized by Ruscheweyh [9].Definition 4: A function 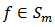 is said to be in the class
is said to be in the class 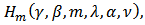 if there exist a function
if there exist a function 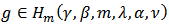 such that
such that Theorem 10: If
Theorem 10: If 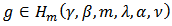 and
and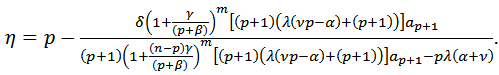 | (28) |
Then 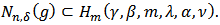 Proof: Let
Proof: Let 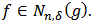 Then we have from (26) that
Then we have from (26) that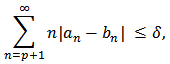 which readily implies the following coefficient inequality
which readily implies the following coefficient inequality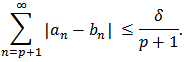 Next, since
Next, since 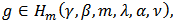 we have from Theorem 1
we have from Theorem 1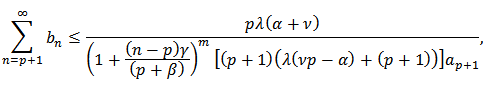 so that
so that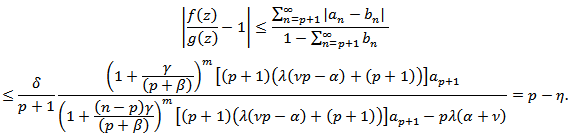 Then by Definition 3,
Then by Definition 3, 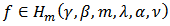 for every
for every 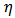 given by (28).Now, we introduce the partial sums.Theorem 11: Let
given by (28).Now, we introduce the partial sums.Theorem 11: Let 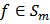 be given by (2) and define the
be given by (2) and define the 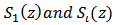 by
by 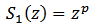 and
and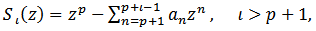 | (30) |
suppose also that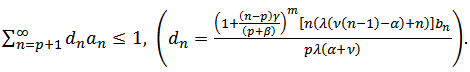 | (31) |
Thus, we have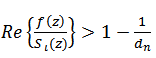 | (32) |
and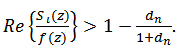 | (33) |
Each of the bounds in (32) and (33) is the best possible for 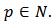 Proof: For the coefficients
Proof: For the coefficients 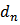 given by (31), it is not difficult to verity that
given by (31), it is not difficult to verity that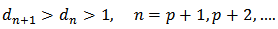 Therefore, by using the hypothesis (30), we have
Therefore, by using the hypothesis (30), we have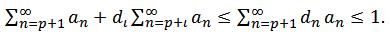 | (34) |
By setting 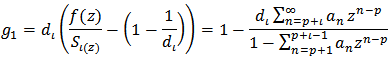 and applying (34), we find that
and applying (34), we find that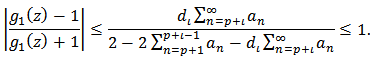 This prove (32). Therefore,
This prove (32). Therefore, 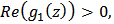 and we obtain
and we obtain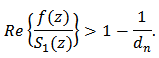 Now, in the same manner, we prove the assertion(33), by setting
Now, in the same manner, we prove the assertion(33), by setting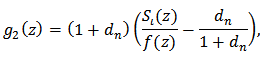 and this completes the proof.
and this completes the proof.
References
| [1] | W. G. Atshan, On a certain class of multivalent functions defined by Hadamard product, Journal of Asian Scientific Research, 3(9)(2013), : 891-902. |
| [2] | W. G. Atshan and A. S. Joudah, Subclass of meromorphic univalent functions defined by Hadamard product with multiplier transformation, Int. Math. Forum, 6(46) (2011), 2279-2292. |
| [3] | W. G. Atshan and S. R. Kulkarni, On application of differential subordination for certain subclass of meromorphically p-valent functions with positive coefficients defined by linear operator, J. Ineq. Pute Appl. Math., 10(2)(2009), Articale 53, 11 pages. |
| [4] | W. G. Atshan, H. J. Mustafa and E. k. Mouajueed, Subclass of multivalent functions defined by Hadamard product involving a linear operator, Int. Journal of Math. Analysis Vol 7. 2013, no. 24, 1193-1206. |
| [5] | A. W. Goodman, Univalent functions and non-analytic curves, Proc. Amer. Math. Soc., 8(3)(1957), 598-601. |
| [6] | S. M. Khairua and M. More, Some analytic and multivalent functions defined by subordination property. Gen. Math. 17(3) (2009) 105-124. |
| [7] | H. Mahzoon, New subclass of multivalent functions defined by differential subordination. Appl. Math. Sciences, 6(95) (2012), 4701. |
| [8] | H. Mahzoon and S. Latha, Neighborhoods of multivalent functions, Int. Journal of Math. Anlysis, 3(30) (2009), 15011-1507. |
| [9] | S. Rucheweyh, Neighborhoods of univalent functions, Proc. Amer. Math. Soc. 81(1981), 521-527. |

 we obtain some interesting properties, like, coefficient inequality, distortion bounds, closure theorems, radii of starlikeness, convexity and close-to-convexity, weighted mean, neighborhoods and partial sums.
we obtain some interesting properties, like, coefficient inequality, distortion bounds, closure theorems, radii of starlikeness, convexity and close-to-convexity, weighted mean, neighborhoods and partial sums.
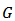 denote the class of all functions of the from
denote the class of all functions of the from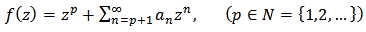
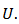 Let
Let 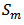 denote the subclass of
denote the subclass of 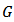 consisting of functions of the from
consisting of functions of the from 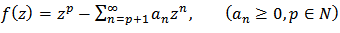
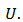 For the function
For the function 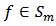 given by (2) and
given by (2) and 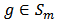 defined by
defined by 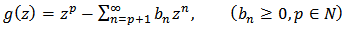
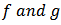 by
by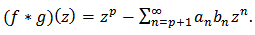
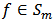 is said to be p-valentlystarlike of order
is said to be p-valentlystarlike of order 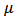 if and only if
if and only if 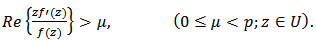
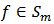 is said to be p-valently convex of order
is said to be p-valently convex of order 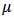 if and only if
if and only if
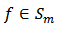 is said to be p-valently close-to-convex of order
is said to be p-valently close-to-convex of order 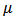 if and only if
if and only if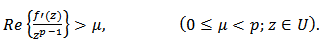
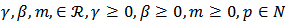 and
and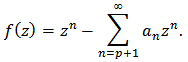 Then we define the linear operator
Then we define the linear operator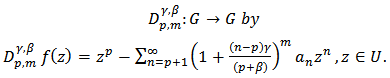
 be a fixed function defined by (3). The function
be a fixed function defined by (3). The function  given by (2) is said to be in the class
given by (2) is said to be in the class  if and only if
if and only if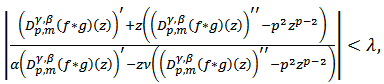
 Some of the following properties studied for other class in [1], [2], [3], [4], [6] and [7].
Some of the following properties studied for other class in [1], [2], [3], [4], [6] and [7].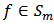 . Then
. Then 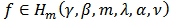 if and only if
if and only if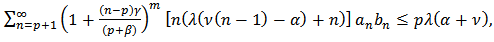
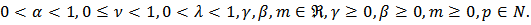 The result is sharp for the function
The result is sharp for the function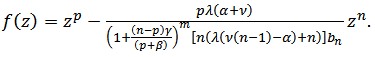
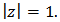 Then we have
Then we have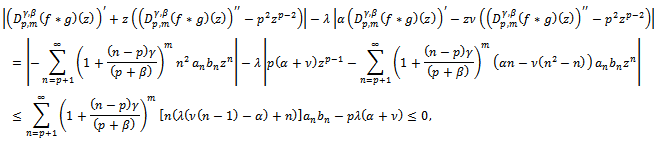 by hypothesis.Hence, by maximum modulus principle,
by hypothesis.Hence, by maximum modulus principle, 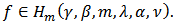 Conversely, suppose that
Conversely, suppose that 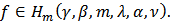 Then from (9), we have
Then from (9), we have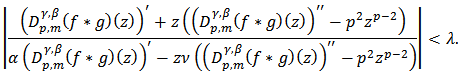 Since
Since 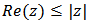 for all
for all 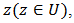 we get
we get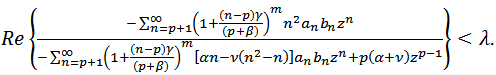
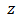 on the real axis, so that
on the real axis, so that 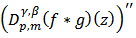 is real.Letting
is real.Letting 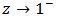 through real values, we obtain inequality (10).Finally, sharpness follows if we take
through real values, we obtain inequality (10).Finally, sharpness follows if we take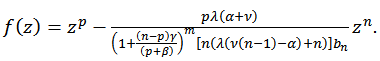
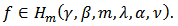 Then
Then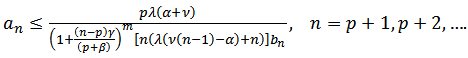
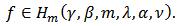 Then
Then 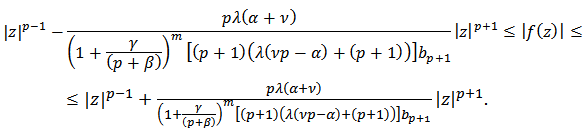
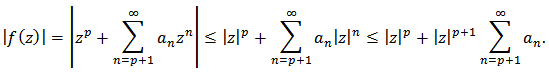 By Theorem 1, we get
By Theorem 1, we get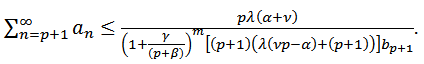
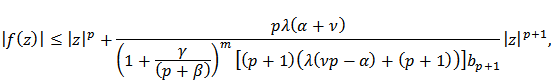 also
also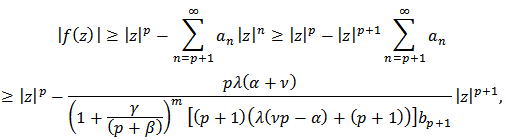 and the proof is complete.Theorem 3: Let
and the proof is complete.Theorem 3: Let 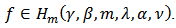 Then
Then 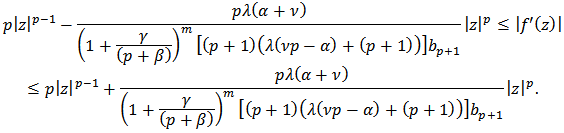 Proof: Notice that
Proof: Notice that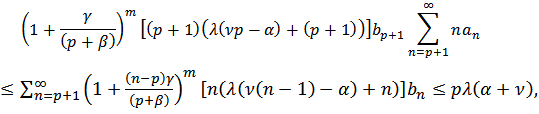
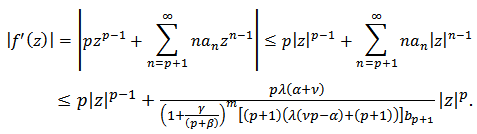
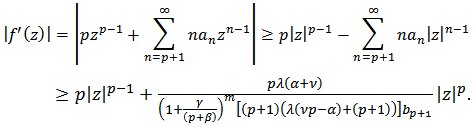
 defined by
defined by
 for every
for every 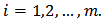 Then the function
Then the function 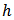 defined by
defined by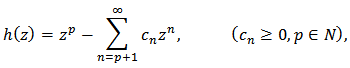 also belongs to the class
also belongs to the class 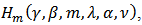 where
where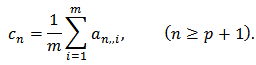 Proof: Since
Proof: Since 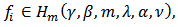 then by Theorem 1, we have
then by Theorem 1, we have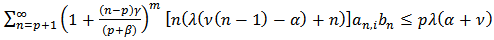
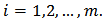 Hence
Hence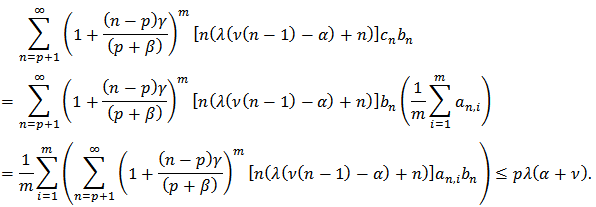 By Theorem 1, it follows that
By Theorem 1, it follows that 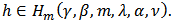 Theorem 5: Let the function
Theorem 5: Let the function 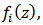 defined by (20) be in the class
defined by (20) be in the class  for every
for every 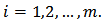 Then the function
Then the function 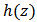 defined by
defined by 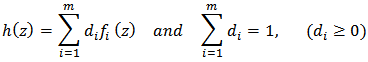 is also in the class
is also in the class 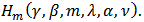 Proof: By definition of
Proof: By definition of 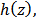 we have
we have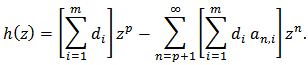 Since
Since 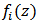 are in the class
are in the class 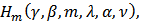 for every
for every 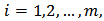 we obtain
we obtain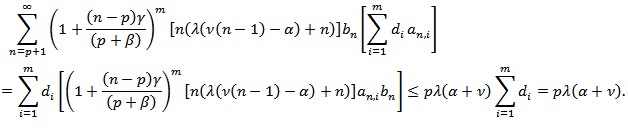
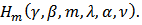 Theorem 6: If
Theorem 6: If 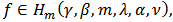 then
then 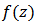 is p-valentlystarlike of order
is p-valentlystarlike of order 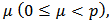 in the dick
in the dick 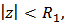 where
where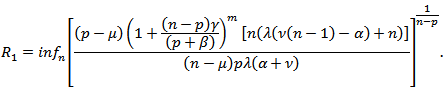 Proof: It is sufficient to show that
Proof: It is sufficient to show that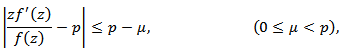 for
for 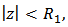 we have
we have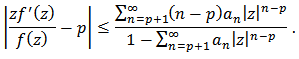 Thus
Thus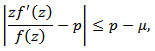 if
if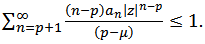
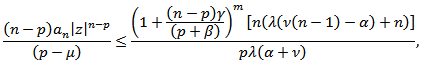 or if
or if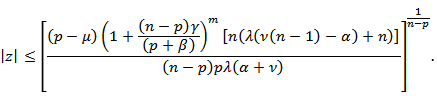 Setting
Setting 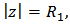 we get the desired result.Theorem 7: If
we get the desired result.Theorem 7: If 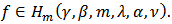 Then
Then 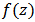 is p-valently convex of order
is p-valently convex of order 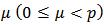 in the disk
in the disk 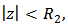 where
where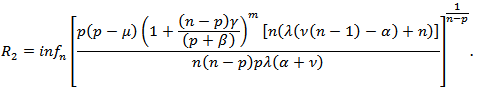 Proof: It is sufficient to show that
Proof: It is sufficient to show that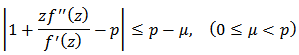 for
for 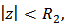 we have
we have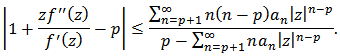 Thus
Thus 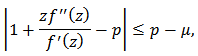 if
if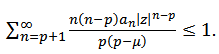
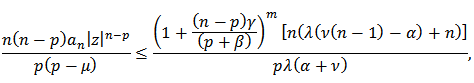 and hence
and hence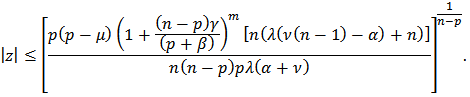 Setting
Setting 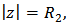 we get the desired result.Theorem 8: Let the function
we get the desired result.Theorem 8: Let the function 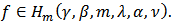 Then
Then 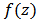 is p-valently close-to-convex of order
is p-valently close-to-convex of order 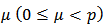 in the disk
in the disk 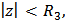 where
where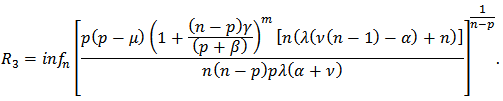 Proof: It is sufficient to show that
Proof: It is sufficient to show that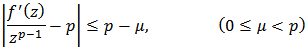 for
for 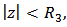 we have
we have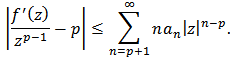 Thus
Thus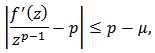 if
if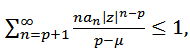
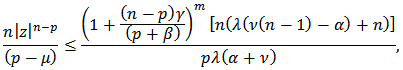 and hence
and hence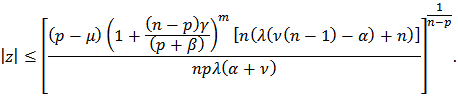 Setting
Setting 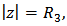 we get the desired result.
we get the desired result. be in the class
be in the class 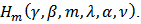 Then the weighted mean
Then the weighted mean 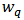 of
of 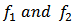 is given by
is given by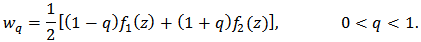 Theorem 9: Let
Theorem 9: Let 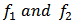 be in the class
be in the class 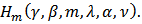 Then the weighted mean
Then the weighted mean 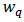 of
of 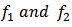 is also in the class
is also in the class 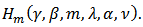 Poof: By Definition 3, we have
Poof: By Definition 3, we have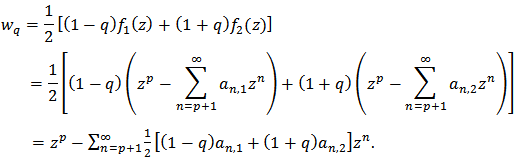
 are in the class
are in the class  so by Theorem 1, we get
so by Theorem 1, we get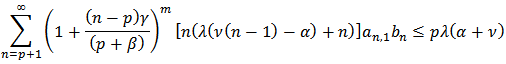 and
and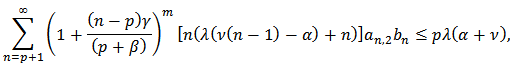 Hence
Hence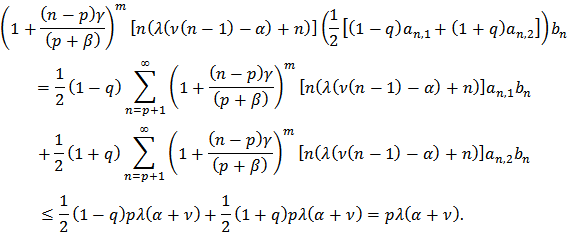 Therefore
Therefore 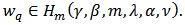 The proof is complete.
The proof is complete.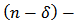 neighborhoods of the function
neighborhoods of the function 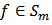 by
by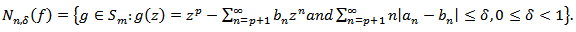
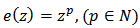
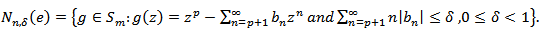
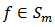 is said to be in the class
is said to be in the class 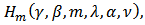 if there exist a function
if there exist a function 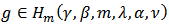 such that
such that Theorem 10: If
Theorem 10: If 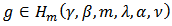 and
and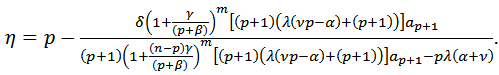
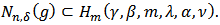 Proof: Let
Proof: Let 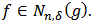 Then we have from (26) that
Then we have from (26) that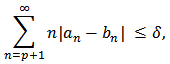 which readily implies the following coefficient inequality
which readily implies the following coefficient inequality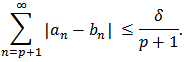 Next, since
Next, since 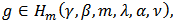 we have from Theorem 1
we have from Theorem 1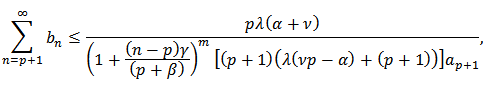 so that
so that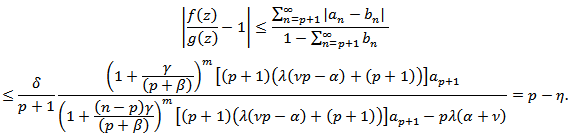 Then by Definition 3,
Then by Definition 3, 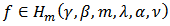 for every
for every 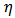 given by (28).Now, we introduce the partial sums.Theorem 11: Let
given by (28).Now, we introduce the partial sums.Theorem 11: Let 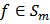 be given by (2) and define the
be given by (2) and define the 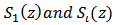 by
by 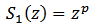 and
and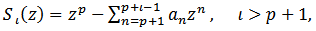
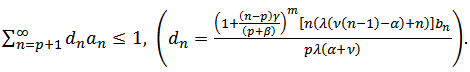
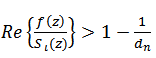
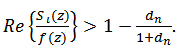
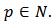 Proof: For the coefficients
Proof: For the coefficients 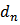 given by (31), it is not difficult to verity that
given by (31), it is not difficult to verity that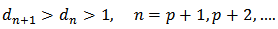 Therefore, by using the hypothesis (30), we have
Therefore, by using the hypothesis (30), we have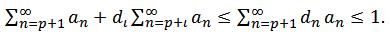
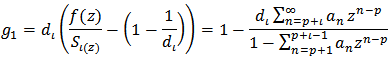 and applying (34), we find that
and applying (34), we find that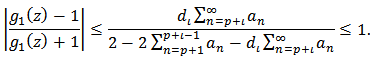 This prove (32). Therefore,
This prove (32). Therefore, 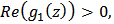 and we obtain
and we obtain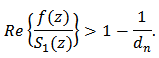 Now, in the same manner, we prove the assertion(33), by setting
Now, in the same manner, we prove the assertion(33), by setting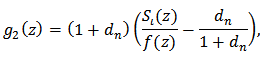 and this completes the proof.
and this completes the proof. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML