Abid A. Al-Ta'ai, Hoor M. Hussein
Department of Mathematics, College of Education, Al-Mustansiriya University
Correspondence to: Abid A. Al-Ta'ai, Department of Mathematics, College of Education, Al-Mustansiriya University.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The universal property of tensor product for representations of Lie groups and Lie algebras is a supporting conjugate of tensor product, which guarantees obtaining a linear map from a bilinear map. The main aim in this study is to look for a novel action with new properties on Lie group from the Lemma of Schure, the literature are concerned with studying the action of Lie algebra of two representations, one is usual and the other is the dual, while our interest in this work is focused on some actions on Lie group. Let G be a matrix Lie group, and 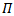 is a representation of G. In this paper we will present and study the concepts of AC-Lie group on Hom space. We recall the definition of tensor product of two representations of Lie groups and construct the definition of AC-Lie group on Hom space; then by using the equivalent relation
is a representation of G. In this paper we will present and study the concepts of AC-Lie group on Hom space. We recall the definition of tensor product of two representations of Lie groups and construct the definition of AC-Lie group on Hom space; then by using the equivalent relation 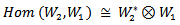 between Hom and Tensor we get a new action AC_Lie group on Tensor product. The two actions are forming smooth representations of G. Also we use the action of Lie group on Hom space
between Hom and Tensor we get a new action AC_Lie group on Tensor product. The two actions are forming smooth representations of G. Also we use the action of Lie group on Hom space 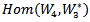 combining with another Hom space having the same structure with different vector space,
combining with another Hom space having the same structure with different vector space, 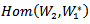 . Thus we have new action which called double action of Lie group G, denoted by AAC_Lie group which acting on
. Thus we have new action which called double action of Lie group G, denoted by AAC_Lie group which acting on 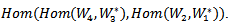 This AAC is smooth representation of G. By using the equivalent relation between Hom space and Tensor product we construct a new AAC_Lie group acting on Tensor product. The theoretical justifications are developed and proved supported by some concluding remarks and illustrations.
This AAC is smooth representation of G. By using the equivalent relation between Hom space and Tensor product we construct a new AAC_Lie group acting on Tensor product. The theoretical justifications are developed and proved supported by some concluding remarks and illustrations.
Keywords:
AC-Lie group, AAC-Lie group, Tensor space, Hom space
Cite this paper: Abid A. Al-Ta'ai, Hoor M. Hussein, The Representation of Lie Group as an Action on Hom Space and Tensor Product, American Journal of Mathematics and Statistics, Vol. 4 No. 2, 2014, pp. 113-120. doi: 10.5923/j.ajms.20140402.07.
1. Introduction
Throughout this paper, In 2004 Hall B. C. [1] wrote a book of Lie group for manifold theory and the relationship between Lie groups and Lie algebras. The reason of studying the representation is that a representation can be thought of as an action of group on some vector space. Such actions (representations) arise naturally in many branches of both mathematics and physics [5], [6], and it is important to understand them. In [1], the Schur's lemma introduced the concept of action of Lie algebra on the space of linear maps from 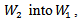 which denoted by
which denoted by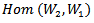 , also introduce the concept of action on tensor product of two representation of Lie algebra.Schur's lemma state: Suppose that
, also introduce the concept of action on tensor product of two representation of Lie algebra.Schur's lemma state: Suppose that 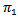 and
and 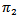 are representation of lie algebra acting. On finite – dimensional space
are representation of lie algebra acting. On finite – dimensional space 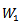 and
and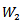 , respectively. Define an action of g on
, respectively. Define an action of g on 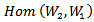
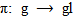
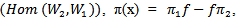 for all x∊g and f
for all x∊g and f 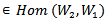 . and
. and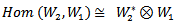 , as equivalence of representation.In [4], T. H. Majeed study the AAC of Lie group on
, as equivalence of representation.In [4], T. H. Majeed study the AAC of Lie group on 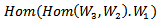 and translation it to AAC _Lie algebra on
and translation it to AAC _Lie algebra on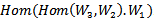 .In this paper we will present and study the concept of action on
.In this paper we will present and study the concept of action on 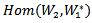 and the equivalent relation with the tensor product space. since
and the equivalent relation with the tensor product space. since 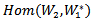 is a vector space of all linear functional from
is a vector space of all linear functional from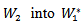 , so
, so 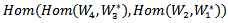 is also vector space of all linear functional from
is also vector space of all linear functional from 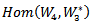 into
into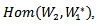 then the representation of G acting on this vector is action of G on this Hom space. Also we give an equivalent relation between AC_Lie group and AAC_Lie group on Hom and AC_Lie group with AAC_Lie group on Tensor products, and explain the actions structure by using diagram.
then the representation of G acting on this vector is action of G on this Hom space. Also we give an equivalent relation between AC_Lie group and AAC_Lie group on Hom and AC_Lie group with AAC_Lie group on Tensor products, and explain the actions structure by using diagram.
2. Basic Definition
Definition (2.1) [2]: A Lie group G is a finite dimensional smooth manifold G together with a group structure on G, such that the multiplication 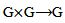 and the attaching of an inverse
and the attaching of an inverse 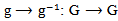 are smooth maps.Definition (2.2) [3]: A matrix Lie group is any subgroup
are smooth maps.Definition (2.2) [3]: A matrix Lie group is any subgroup 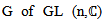 with the following property. If is any sequence of matrices in G and Am converges to some matrix A then A ∈ G, or A is not invertible.Definition (2.3) [7]: A finite-dimensional real (complex) representation of G is a Lie group homomorphism
with the following property. If is any sequence of matrices in G and Am converges to some matrix A then A ∈ G, or A is not invertible.Definition (2.3) [7]: A finite-dimensional real (complex) representation of G is a Lie group homomorphism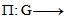
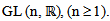 Generally, a Lie group homomorphism
Generally, a Lie group homomorphism 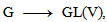 where V is a finite dimensional real (complex) vector space with dim V ≥ 1.Definition (2.4) [7]: Let G and H are two Lie groups. A map f from G to H is called a Lie group homomorphism if f is a group homomorphism and
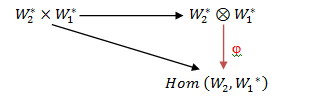
where V is a finite dimensional real (complex) vector space with dim V ≥ 1.Definition (2.4) [7]: Let G and H are two Lie groups. A map f from G to H is called a Lie group homomorphism if f is a group homomorphism and  -map on H.Definition (2.5) [1]: If U and V are finite dimensional real or complex vector spaces, then a tensor product of U and V is a vector space W, together with a bilinear map
-map on H.Definition (2.5) [1]: If U and V are finite dimensional real or complex vector spaces, then a tensor product of U and V is a vector space W, together with a bilinear map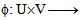
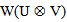 with the following property: If ψ is any bilinear map of
with the following property: If ψ is any bilinear map of 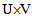 into a vector space W1, then there exists a unique linear map
into a vector space W1, then there exists a unique linear map 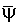 of W into W1, such that the following diagram commutes:
of W into W1, such that the following diagram commutes: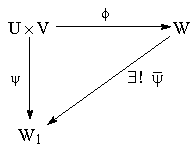
3. The Action of Lie Group on Hom Space
In this section we define an action of G on 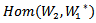 and give the equivalent relation with representation acting on the tensor space.Note (3.1):
and give the equivalent relation with representation acting on the tensor space.Note (3.1): | Diagram (1) |
Put  the vector space of all linear maps from
the vector space of all linear maps from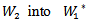 , where
, where 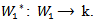 we define an action of Lie group G on
we define an action of Lie group G on 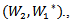 which given by:
which given by: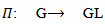
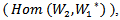 define by:
define by: 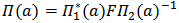 For all a∊G, and F= F2ₒ
For all a∊G, and F= F2ₒ 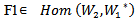 ,
, 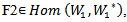
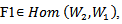
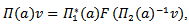
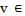
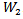 .this diagram(1) will show the structure of this action.Proposition (3.2): Let
.this diagram(1) will show the structure of this action.Proposition (3.2): Let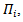 i=1, 2; be representation of lie group G acting on
i=1, 2; be representation of lie group G acting on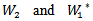 , then
, then 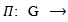
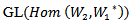 is a representation of Lie group acting on
is a representation of Lie group acting on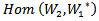 , which called AC_Lie group on
, which called AC_Lie group on 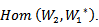 Proof:Since
Proof:Since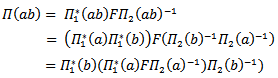 | (1) |
And 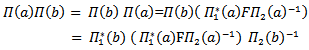 | (2) |
Then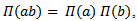 Thus by
Thus by 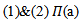 is a representation of G. The following diagram (2) shows that
is a representation of G. The following diagram (2) shows that 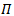 is a group homomorphism:
is a group homomorphism: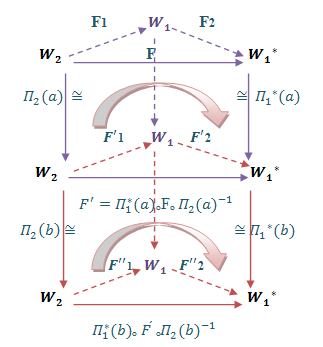 | Diagram (2) |
Where 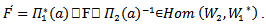 Also
Also 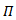 is a continuous map since the composition of continuous map is continuous. See diagram (3).
is a continuous map since the composition of continuous map is continuous. See diagram (3). 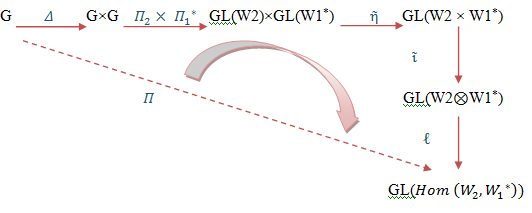 | Diagram (3) |
Hence 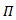 is a representation of Lie group G, since every continuous homomorphism is smoothExample (3.3): Suppose that
is a representation of Lie group G, since every continuous homomorphism is smoothExample (3.3): Suppose that 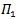 be a representation from G into
be a representation from G into 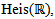 such that
such that Proposition(3.4): Let
Proposition(3.4): Let 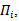 i=1,2 ;be representation of lie group G acting on
i=1,2 ;be representation of lie group G acting on 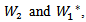 then
then 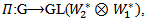 is a representation of G acting on the vector space
is a representation of G acting on the vector space 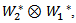 such that:
such that: 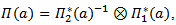 for all a∊G.
for all a∊G.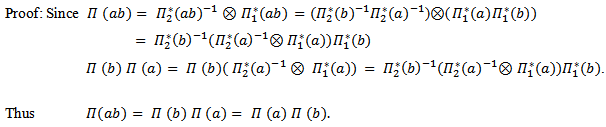
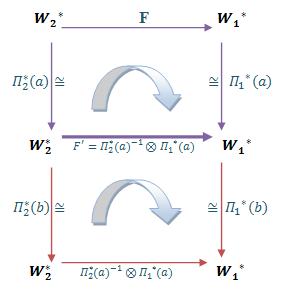 | Diagram (4) |
The diagram (4) use to show that  is a group homomorphism of G on
is a group homomorphism of G on  And also
And also  it is smooth maps. The diagram (5) is to show smoothness of this representation:
it is smooth maps. The diagram (5) is to show smoothness of this representation: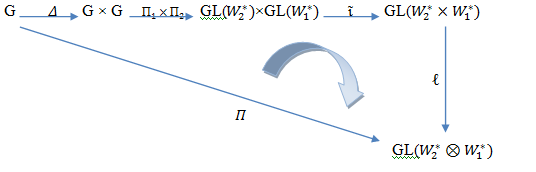 | Diagram (5) |
The diagonal map 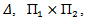 inclusion map
inclusion map 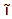 and bilinear map
and bilinear map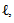 are smooth hence the composition of this are smooth. Hence
are smooth hence the composition of this are smooth. Hence 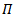 is smooth representation.Proposition (3.5): Let
is smooth representation.Proposition (3.5): Let 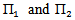 be a representation of G acting on k-finite dimensional vector space
be a representation of G acting on k-finite dimensional vector space 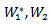 respectively, then the AC _lie group of G on
respectively, then the AC _lie group of G on 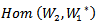 is equivalent to the AC_lie group on
is equivalent to the AC_lie group on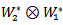 .Proof: To show that
.Proof: To show that 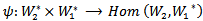 is a bilinear map, defined by:
is a bilinear map, defined by: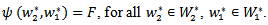 Where
Where 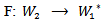 is a linear map, defined by:
is a linear map, defined by: 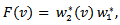 For all
For all 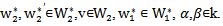
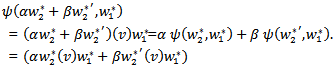 Other for all
Other for all 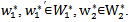
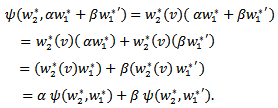 So
So 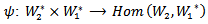 is a bilinear map, thus by using the tensor product and universal property of this tensor product, we get a unique linear map
is a bilinear map, thus by using the tensor product and universal property of this tensor product, we get a unique linear map 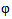
 So by universal property of tensor product
So by universal property of tensor product 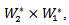 there exists a unique linear map
there exists a unique linear map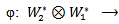
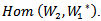 this makes the above diagram commutative.
this makes the above diagram commutative.
4. AAC-Lie Group on Hom and Tensor Product
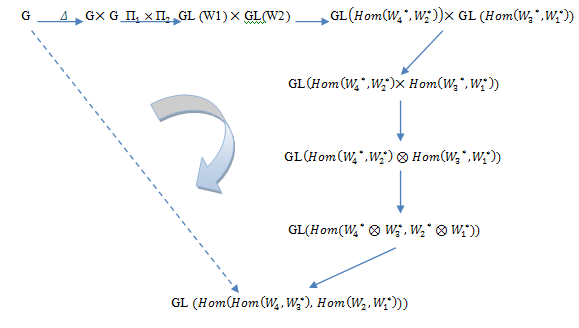
In this section we construct an action on the space of all linear functional from 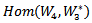 into
into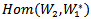 .Definition (4.1): Let
.Definition (4.1): Let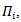 i=1,2,3,4 be a representation o f Lie group G acting on finite dimensional vector space
i=1,2,3,4 be a representation o f Lie group G acting on finite dimensional vector space 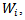 for i=1,2,3,4, then the representation of G acting on
for i=1,2,3,4, then the representation of G acting on 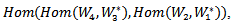 form an action, defined by:
form an action, defined by: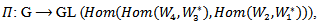 such that:
such that: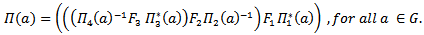 This diagram will show the structure of this representation:
This diagram will show the structure of this representation: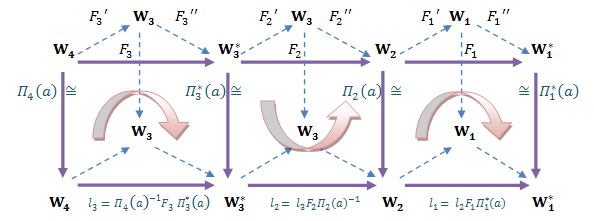 | Diagram (6) |
Proposition (4.2): Let 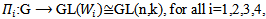 be a representation of G acting on
be a representation of G acting on 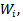 then
then 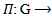
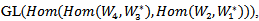 such that
such that 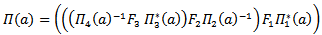
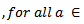
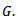 is a representation of G.Proof: Firstly we must show that
is a representation of G.Proof: Firstly we must show that 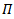 is a group homomorphism. The diagram (7) below is to show proving of group homomorphism.
is a group homomorphism. The diagram (7) below is to show proving of group homomorphism. | Diagram (7) |
Secondly to prove 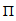 is continuous, let
is continuous, let 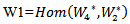 and
and 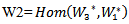 be two finite vector spaces such that
be two finite vector spaces such that 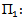
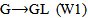 and
and 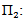
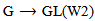 be two representation acting on W1 and W2 respectively. Diagram (8) show continuity of
be two representation acting on W1 and W2 respectively. Diagram (8) show continuity of 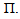
 | Diagram (8) |
Hence 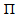 is a representation of G, since every continuous homomorphism is smooth.Proposition (4.3): Let
is a representation of G, since every continuous homomorphism is smooth.Proposition (4.3): Let 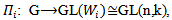 for all i=1,2,3,4, be a representation of G acting on
for all i=1,2,3,4, be a representation of G acting on 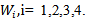 then
then 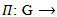
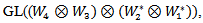 such that:
such that: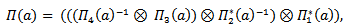 for all a∈G.Is a representation of G.Proof: Diagram (9) below illustrates the process of proof group homomorphism.
for all a∈G.Is a representation of G.Proof: Diagram (9) below illustrates the process of proof group homomorphism.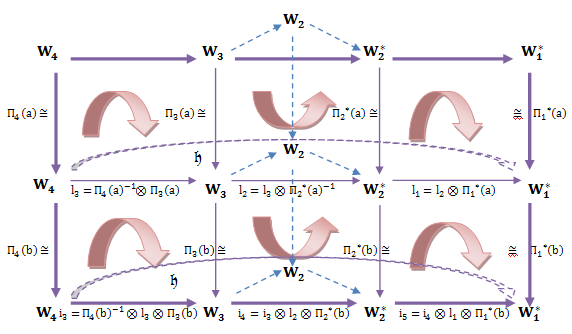 | Diagram (9) |
Diagram (10) below illustrates the process of continuity. Since the composition of continuous map is continuous. | Diagram (10) |
Hence  is a representation of G, since every continuous homomorphism is smooth.Example (4.4): Let
is a representation of G, since every continuous homomorphism is smooth.Example (4.4): Let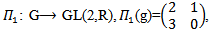 And
And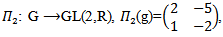
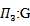
 GL(2,R),
GL(2,R), 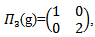 and
and 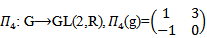 then the AAC-lie group on hom is:
then the AAC-lie group on hom is:
References
| [1] | Hall, B. C., "Lie Groups, Lie Algebras and Representations, An Elementary Introduction", Springer, USA, May, 2004. |
| [2] | Keith Jones, "Notes on Lie Groups", December 25, 2007, kjones@math.binghamton.edu |
| [3] | STILLWELL, JOHN, Naive Lie theory. Undergraduate Texts in Mathematics. Springer, New York, 2008. |
| [4] | Taghreed H. M., "The Universal Property of Tensor Product for Representations of Lie Groups", Thesis of Doctor of Philosophy, College of Education, Al-Mustansiriyah University, 2010. |
| [5] | Usenko, V. and Lev, I. B., "Spinor Representation of Lie Algebra for Complete Linear Group", Uktaine, 46, Nauky. Ave, NAS, Vol.50, Part 3, pp.1202-1206. |
| [6] | Wan, Z. X., "Lie Algebras", Translated by Lee, Che-Young, ISBN, Volume 104, 1975. |
| [7] | Wolfgang Ziller," Lie Groups. Representation Theory and Symmetric Spaces" University of Pennsylvania, Fall 2010. |
 is a representation of G. In this paper we will present and study the concepts of AC-Lie group on Hom space. We recall the definition of tensor product of two representations of Lie groups and construct the definition of AC-Lie group on Hom space; then by using the equivalent relation
is a representation of G. In this paper we will present and study the concepts of AC-Lie group on Hom space. We recall the definition of tensor product of two representations of Lie groups and construct the definition of AC-Lie group on Hom space; then by using the equivalent relation 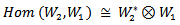 between Hom and Tensor we get a new action AC_Lie group on Tensor product. The two actions are forming smooth representations of G. Also we use the action of Lie group on Hom space
between Hom and Tensor we get a new action AC_Lie group on Tensor product. The two actions are forming smooth representations of G. Also we use the action of Lie group on Hom space 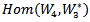 combining with another Hom space having the same structure with different vector space,
combining with another Hom space having the same structure with different vector space, 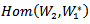 . Thus we have new action which called double action of Lie group G, denoted by AAC_Lie group which acting on
. Thus we have new action which called double action of Lie group G, denoted by AAC_Lie group which acting on 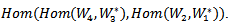 This AAC is smooth representation of G. By using the equivalent relation between Hom space and Tensor product we construct a new AAC_Lie group acting on Tensor product. The theoretical justifications are developed and proved supported by some concluding remarks and illustrations.
This AAC is smooth representation of G. By using the equivalent relation between Hom space and Tensor product we construct a new AAC_Lie group acting on Tensor product. The theoretical justifications are developed and proved supported by some concluding remarks and illustrations.
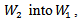 which denoted by
which denoted by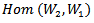 , also introduce the concept of action on tensor product of two representation of Lie algebra.Schur's lemma state: Suppose that
, also introduce the concept of action on tensor product of two representation of Lie algebra.Schur's lemma state: Suppose that  and
and  are representation of lie algebra acting. On finite – dimensional space
are representation of lie algebra acting. On finite – dimensional space 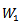 and
and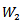 , respectively. Define an action of g on
, respectively. Define an action of g on 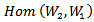
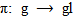
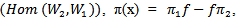 for all x∊g and f
for all x∊g and f 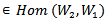 . and
. and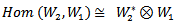 , as equivalence of representation.In [4], T. H. Majeed study the AAC of Lie group on
, as equivalence of representation.In [4], T. H. Majeed study the AAC of Lie group on 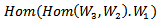 and translation it to AAC _Lie algebra on
and translation it to AAC _Lie algebra on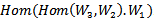 .In this paper we will present and study the concept of action on
.In this paper we will present and study the concept of action on 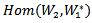 and the equivalent relation with the tensor product space. since
and the equivalent relation with the tensor product space. since 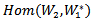 is a vector space of all linear functional from
is a vector space of all linear functional from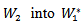 , so
, so 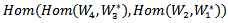 is also vector space of all linear functional from
is also vector space of all linear functional from 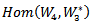 into
into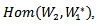 then the representation of G acting on this vector is action of G on this Hom space. Also we give an equivalent relation between AC_Lie group and AAC_Lie group on Hom and AC_Lie group with AAC_Lie group on Tensor products, and explain the actions structure by using diagram.
then the representation of G acting on this vector is action of G on this Hom space. Also we give an equivalent relation between AC_Lie group and AAC_Lie group on Hom and AC_Lie group with AAC_Lie group on Tensor products, and explain the actions structure by using diagram.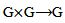 and the attaching of an inverse
and the attaching of an inverse 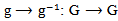 are smooth maps.Definition (2.2) [3]: A matrix Lie group is any subgroup
are smooth maps.Definition (2.2) [3]: A matrix Lie group is any subgroup 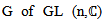 with the following property. If is any sequence of matrices in G and Am converges to some matrix A then A ∈ G, or A is not invertible.Definition (2.3) [7]: A finite-dimensional real (complex) representation of G is a Lie group homomorphism
with the following property. If is any sequence of matrices in G and Am converges to some matrix A then A ∈ G, or A is not invertible.Definition (2.3) [7]: A finite-dimensional real (complex) representation of G is a Lie group homomorphism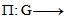
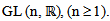 Generally, a Lie group homomorphism
Generally, a Lie group homomorphism 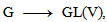 where V is a finite dimensional real (complex) vector space with dim V ≥ 1.Definition (2.4) [7]: Let G and H are two Lie groups. A map f from G to H is called a Lie group homomorphism if f is a group homomorphism and
where V is a finite dimensional real (complex) vector space with dim V ≥ 1.Definition (2.4) [7]: Let G and H are two Lie groups. A map f from G to H is called a Lie group homomorphism if f is a group homomorphism and 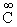 -map on H.Definition (2.5) [1]: If U and V are finite dimensional real or complex vector spaces, then a tensor product of U and V is a vector space W, together with a bilinear map
-map on H.Definition (2.5) [1]: If U and V are finite dimensional real or complex vector spaces, then a tensor product of U and V is a vector space W, together with a bilinear map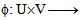
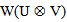 with the following property: If ψ is any bilinear map of
with the following property: If ψ is any bilinear map of 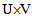 into a vector space W1, then there exists a unique linear map
into a vector space W1, then there exists a unique linear map 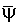 of W into W1, such that the following diagram commutes:
of W into W1, such that the following diagram commutes:
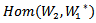 and give the equivalent relation with representation acting on the tensor space.Note (3.1):
and give the equivalent relation with representation acting on the tensor space.Note (3.1):
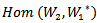 the vector space of all linear maps from
the vector space of all linear maps from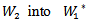 , where
, where 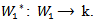 we define an action of Lie group G on
we define an action of Lie group G on 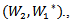 which given by:
which given by: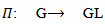
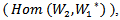 define by:
define by: 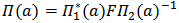 For all a∊G, and F= F2ₒ
For all a∊G, and F= F2ₒ 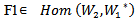 ,
, 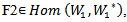
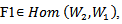
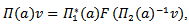
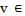
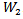 .this diagram(1) will show the structure of this action.Proposition (3.2): Let
.this diagram(1) will show the structure of this action.Proposition (3.2): Let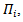 i=1, 2; be representation of lie group G acting on
i=1, 2; be representation of lie group G acting on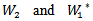 , then
, then 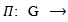
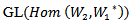 is a representation of Lie group acting on
is a representation of Lie group acting on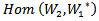 , which called AC_Lie group on
, which called AC_Lie group on 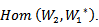 Proof:Since
Proof:Since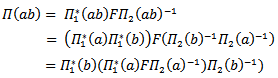
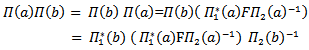
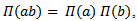 Thus by
Thus by 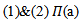 is a representation of G. The following diagram (2) shows that
is a representation of G. The following diagram (2) shows that 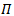 is a group homomorphism:
is a group homomorphism:
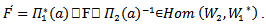 Also
Also 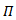 is a continuous map since the composition of continuous map is continuous. See diagram (3).
is a continuous map since the composition of continuous map is continuous. See diagram (3). 
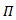 is a representation of Lie group G, since every continuous homomorphism is smoothExample (3.3): Suppose that
is a representation of Lie group G, since every continuous homomorphism is smoothExample (3.3): Suppose that 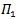 be a representation from G into
be a representation from G into 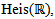 such that
such that Proposition(3.4): Let
Proposition(3.4): Let 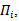 i=1,2 ;be representation of lie group G acting on
i=1,2 ;be representation of lie group G acting on 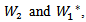 then
then 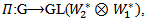 is a representation of G acting on the vector space
is a representation of G acting on the vector space 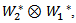 such that:
such that: 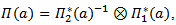 for all a∊G.
for all a∊G.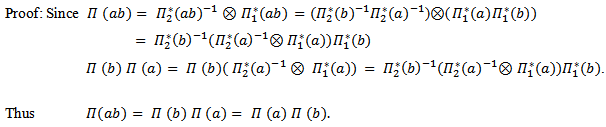

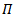 is a group homomorphism of G on
is a group homomorphism of G on  And also
And also 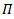 it is smooth maps. The diagram (5) is to show smoothness of this representation:
it is smooth maps. The diagram (5) is to show smoothness of this representation:
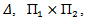 inclusion map
inclusion map 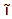 and bilinear map
and bilinear map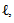 are smooth hence the composition of this are smooth. Hence
are smooth hence the composition of this are smooth. Hence 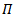 is smooth representation.Proposition (3.5): Let
is smooth representation.Proposition (3.5): Let 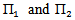 be a representation of G acting on k-finite dimensional vector space
be a representation of G acting on k-finite dimensional vector space 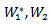 respectively, then the AC _lie group of G on
respectively, then the AC _lie group of G on 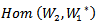 is equivalent to the AC_lie group on
is equivalent to the AC_lie group on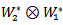 .Proof: To show that
.Proof: To show that 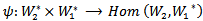 is a bilinear map, defined by:
is a bilinear map, defined by: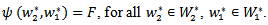 Where
Where 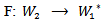 is a linear map, defined by:
is a linear map, defined by: 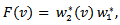 For all
For all 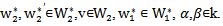
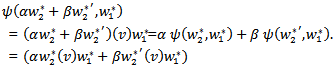 Other for all
Other for all 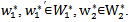
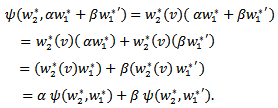 So
So 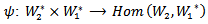 is a bilinear map, thus by using the tensor product and universal property of this tensor product, we get a unique linear map
is a bilinear map, thus by using the tensor product and universal property of this tensor product, we get a unique linear map 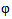
 So by universal property of tensor product
So by universal property of tensor product 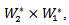 there exists a unique linear map
there exists a unique linear map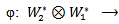
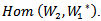 this makes the above diagram commutative.
this makes the above diagram commutative.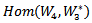 into
into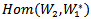 .Definition (4.1): Let
.Definition (4.1): Let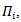 i=1,2,3,4 be a representation o f Lie group G acting on finite dimensional vector space
i=1,2,3,4 be a representation o f Lie group G acting on finite dimensional vector space 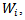 for i=1,2,3,4, then the representation of G acting on
for i=1,2,3,4, then the representation of G acting on 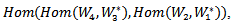 form an action, defined by:
form an action, defined by: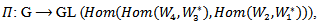 such that:
such that: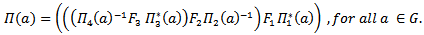 This diagram will show the structure of this representation:
This diagram will show the structure of this representation:
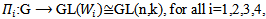 be a representation of G acting on
be a representation of G acting on 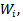 then
then 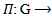
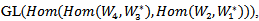 such that
such that 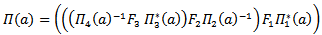
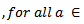
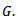 is a representation of G.Proof: Firstly we must show that
is a representation of G.Proof: Firstly we must show that 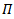 is a group homomorphism. The diagram (7) below is to show proving of group homomorphism.
is a group homomorphism. The diagram (7) below is to show proving of group homomorphism.
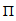 is continuous, let
is continuous, let 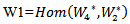 and
and 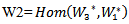 be two finite vector spaces such that
be two finite vector spaces such that 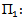
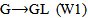 and
and 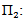
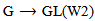 be two representation acting on W1 and W2 respectively. Diagram (8) show continuity of
be two representation acting on W1 and W2 respectively. Diagram (8) show continuity of 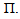

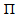 is a representation of G, since every continuous homomorphism is smooth.Proposition (4.3): Let
is a representation of G, since every continuous homomorphism is smooth.Proposition (4.3): Let 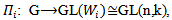 for all i=1,2,3,4, be a representation of G acting on
for all i=1,2,3,4, be a representation of G acting on 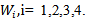 then
then 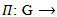
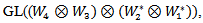 such that:
such that: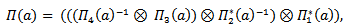 for all a∈G.Is a representation of G.Proof: Diagram (9) below illustrates the process of proof group homomorphism.
for all a∈G.Is a representation of G.Proof: Diagram (9) below illustrates the process of proof group homomorphism.

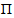 is a representation of G, since every continuous homomorphism is smooth.Example (4.4): Let
is a representation of G, since every continuous homomorphism is smooth.Example (4.4): Let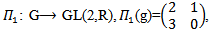 And
And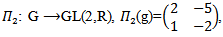
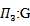
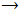 GL(2,R),
GL(2,R), 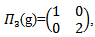 and
and 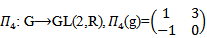 then the AAC-lie group on hom is:
then the AAC-lie group on hom is:
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML