-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2014; 4(2): 80-106
doi:10.5923/j.ajms.20140402.05
Trimmed L-Moments: Analogy of Classical L-Moments
1Department of Statistics and Probability, Faculty of Informatics and Statistics, University of Economics, Prague, 130 67, Czech Republic
2Department of Informatics and Mathematics, Faculty of Economic Studies, University of Finance and Administration, Prague, 101 00, Czech Republic
Correspondence to: Diana Bílková, Department of Statistics and Probability, Faculty of Informatics and Statistics, University of Economics, Prague, 130 67, Czech Republic.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Application of the method of moments for the parametric distribution is common in the construction of a suitable parametric distribution. However, moment method of parameter estimation does not produce good results. An alternative approach when constructing an appropriate parametric distribution for the considered data file is to use the so-called order statistics. This paper deals with the use of the order statistics as the methods of L-moments and TL-moments of parameter estimation. L-moments have some theoretical advantages over conventional moments. L-moments have been introduced as a robust alternative to classical moments of probability distributions. However, L-moments and their estimations lack some robust features that belong to the TL-moments. TL-moments represent an alternative robust version of L-moments, which are called trimmed L-moments. This paper deals with the use of L-moments and TL-moments in the construction of models of wage distribution. Three-parametric lognormal curves represent the basic theoretical distribution whose parameters were simultaneously estimated by three methods of point parameter estimation and accuracy of these methods was then evaluated. There are method of TL-moments, method of L-moments and maximum likelihood method in combination with Cohen’s method. A total of 328 wage distribution has been the subject of research.
Keywords: Order statistics, L-moments, TL-moments, Maximum likelihood method, Probability density function, Distribution function, Quantile function, Lognormal curves, Model of wage distribution
Cite this paper: Diana Bílková, Trimmed L-Moments: Analogy of Classical L-Moments, American Journal of Mathematics and Statistics, Vol. 4 No. 2, 2014, pp. 80-106. doi: 10.5923/j.ajms.20140402.05.
Article Outline
1. Introduction
- Moments and cumulants are traditionally used to characterize the probability distribution or the observed data set in statistics. It is sometimes difficult to determine exactly what information about the shape of the distribution is expressed by its moments of third and higher order. Especially in the case of a small sample, numerical values of sample moments can be very different from the values of theoretical moments of the probability distribution from which the random sample comes. Particularly in the case of small samples, parameter estimations of the probability distribution obtained using the moment method are often markedly less accurate than estimates obtained using other methods, such as maximum likelihood method. An alternative approach is to use the order statistics. Let X be a random variable having a distribution with distribution function F(x) and with quantile function x(F), and let X1, X2, …, Xn is a random sample of sample size n from this distribution. Then
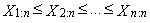 are the order statistics of random sample of sample size n, which comes from the distribution of random variable X.L-moments are analogous to conventional moments and are estimated based on linear combinations of the order statistics, i.e. L-statistics. L-moments are an alternative system describing the shape of the probability distribution. L-moments present the basis for a general theory, which includes the characterization and description of the theoretical probability distribution, characterization and description of the obtained sample data sets, parameter estimation of theoretical probability distribution and hypothesis testing of parameter values for the theoretical probability distribution. The theory of L-moments includes such established procedures such as the use of the order statistics and Gini’s middle difference and leads to some promising innovations in the area of measuring skewness and kurtosis of the distribution and provides relatively new methods of parameter estimation for individual distribution. L-moments can be defined for any random variable whose the expected value exists. The main advantage of the L-moments than conventional moments consists in the fact that L-moments can be estimated on the basis of linear functions of the data and are more resistant to the influence of sample variation. Compared to conventional moments, L-moments are more robust to the existence of outliers in the data and allow better conclusions obtained on the basis of small samples for basic probability distribution. L-moments often bring even more efficient parameter estimations of parametric distribution than the estimations obtained using maximum likelihood method, especially for small samples. Theoretical advantages of L-moments over conventional moments lie in the ability to characterize a wider range of distribution and in greater resistance to the presence of outliers in the data when estimating from the sample. Compared with conventional moments, experience also shows that L-moments are less prone to bias estimation and approximation by asymptotic normal distribution is more accurate in finite samples.Alternative robust version of L-moments will be now presented. This robust modification of L-moments is called “trimmed L-moments” and “labeled TL-moments”.This is a relatively new category of moment characteristics of the probability distribution. There are the characteristics of the level, variability, skewness and kurtosis of probability distributions constructed using TL-moments that are robust extending of L-moments. L-moments alone were introduced as a robust alternative to classical moments of probability distributions. However, L-moments and their estimations lack some robust properties that belong to the TL-moments.Sample TL-moments are linear combinations of the sample order statistics, which assign zero weight to a predetermined number of sample outliers. Sample TL-moments are unbiased estimations of the corresponding TL-moments of probability distributions. Some theoretical and practical aspects of TL-moments are still under research or remain for future research. Efficiency of TL-statistics depends on the choice of α proportion, for example, the first sample TL-moments
are the order statistics of random sample of sample size n, which comes from the distribution of random variable X.L-moments are analogous to conventional moments and are estimated based on linear combinations of the order statistics, i.e. L-statistics. L-moments are an alternative system describing the shape of the probability distribution. L-moments present the basis for a general theory, which includes the characterization and description of the theoretical probability distribution, characterization and description of the obtained sample data sets, parameter estimation of theoretical probability distribution and hypothesis testing of parameter values for the theoretical probability distribution. The theory of L-moments includes such established procedures such as the use of the order statistics and Gini’s middle difference and leads to some promising innovations in the area of measuring skewness and kurtosis of the distribution and provides relatively new methods of parameter estimation for individual distribution. L-moments can be defined for any random variable whose the expected value exists. The main advantage of the L-moments than conventional moments consists in the fact that L-moments can be estimated on the basis of linear functions of the data and are more resistant to the influence of sample variation. Compared to conventional moments, L-moments are more robust to the existence of outliers in the data and allow better conclusions obtained on the basis of small samples for basic probability distribution. L-moments often bring even more efficient parameter estimations of parametric distribution than the estimations obtained using maximum likelihood method, especially for small samples. Theoretical advantages of L-moments over conventional moments lie in the ability to characterize a wider range of distribution and in greater resistance to the presence of outliers in the data when estimating from the sample. Compared with conventional moments, experience also shows that L-moments are less prone to bias estimation and approximation by asymptotic normal distribution is more accurate in finite samples.Alternative robust version of L-moments will be now presented. This robust modification of L-moments is called “trimmed L-moments” and “labeled TL-moments”.This is a relatively new category of moment characteristics of the probability distribution. There are the characteristics of the level, variability, skewness and kurtosis of probability distributions constructed using TL-moments that are robust extending of L-moments. L-moments alone were introduced as a robust alternative to classical moments of probability distributions. However, L-moments and their estimations lack some robust properties that belong to the TL-moments.Sample TL-moments are linear combinations of the sample order statistics, which assign zero weight to a predetermined number of sample outliers. Sample TL-moments are unbiased estimations of the corresponding TL-moments of probability distributions. Some theoretical and practical aspects of TL-moments are still under research or remain for future research. Efficiency of TL-statistics depends on the choice of α proportion, for example, the first sample TL-moments 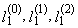 have the smallest variance (the highest efficiency) among other estimations from random samples from normal, logistic and double exponential distribution.When constructing the TL-moments, the expected values of the order statistics of random sample in the definition of L-moments of probability distributions are replaced by the expected values of the order statistics of a larger random sample, where the sample size grows like this, so that it will correspond to the total size of modification, as shown below.TL-moments have certain advantages over conventional L-moments and central moments. TL-moment of probability distribution may exist even if the corresponding L-moment or central moment of the probability distribution does not exist, as it is the case of Cauchy’s distribution. Sample TL-moments are more resistant to existence of outliers in the data. The method of TL-moments is not intended to replace the existing robust methods, but rather as their supplement, especially in situations where we have outliers in the data.
have the smallest variance (the highest efficiency) among other estimations from random samples from normal, logistic and double exponential distribution.When constructing the TL-moments, the expected values of the order statistics of random sample in the definition of L-moments of probability distributions are replaced by the expected values of the order statistics of a larger random sample, where the sample size grows like this, so that it will correspond to the total size of modification, as shown below.TL-moments have certain advantages over conventional L-moments and central moments. TL-moment of probability distribution may exist even if the corresponding L-moment or central moment of the probability distribution does not exist, as it is the case of Cauchy’s distribution. Sample TL-moments are more resistant to existence of outliers in the data. The method of TL-moments is not intended to replace the existing robust methods, but rather as their supplement, especially in situations where we have outliers in the data.2. L-Moments
2.1. L-Moments of Probability Distributions
- Let X be a continuous random variable that has a distribution with distribution function F(x) and with quantile function x(F). Let
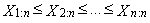 are the order statistics of random sample of sample size n, which comes from the distribution of random variable X. L-moment of the r-th order of random variable X is defined
are the order statistics of random sample of sample size n, which comes from the distribution of random variable X. L-moment of the r-th order of random variable X is defined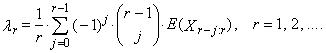 | (1) |
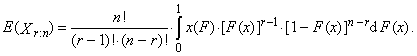 | (2) |
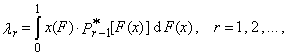 | (3) |
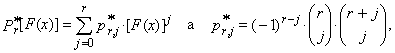 | (4) |
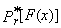 represents the r-th shifted Legendre polynomial. We also obtain substituting (2) into the equation (1)
represents the r-th shifted Legendre polynomial. We also obtain substituting (2) into the equation (1) 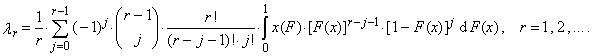 | (5) |
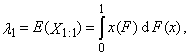 | (6) |
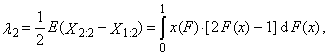 | (7) |
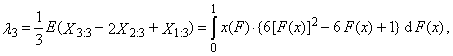 | (8) |
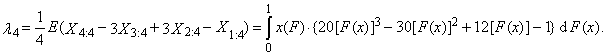 | (9) |
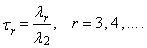 | (10) |
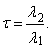 | (11) |
|
2.2. Sample L-Moments
- We usually estimate L-moments using random sample, which is taken from an unknown distribution. Since the r-th L-moment λr is a function of the expected values of the order statistics of random sample of sample size r, it is natural to estimate it using the so-called U-statistic, i.e. the corresponding function of the sample order statistics (averaged over partial subsets of sample size r, which can be formed from the obtained random sample of sample size n).Let x1, x2, …,xn is a sample and
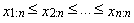 is an ordered sample. Then the r-th sample L-moment can be written as
is an ordered sample. Then the r-th sample L-moment can be written as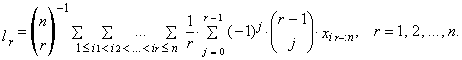 | (12) |
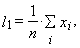 | (13) |
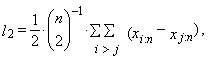 | (14) |
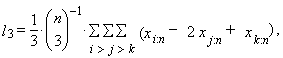 | (15) |
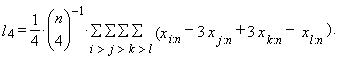 | (16) |
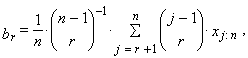 | (17) |
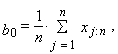 | (18) |
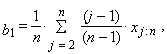 | (19) |
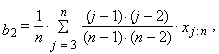 | (20) |
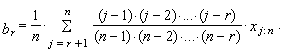 | (21) |
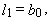 | (22) |
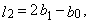 | (23) |
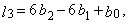 | (24) |
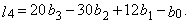 | (25) |
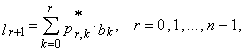 | (26) |
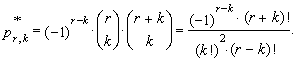 | (27) |
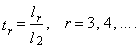 | (28) |
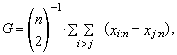 | (29) |
|
3. TL-Moments
3.1. TL-Moments of Probability Distributions
- In this alternative robust modification of L-moments, the expected value E(Xr-j:r) is replaced by the expected value E(Xr+t1−j:r+t1+t2). Thus, for each r we increase the sample size of random sample from the original r to r + t1 + t2 and we work only with the expected values of these r treated order statistics Xt1+1:r+t1+t2, Xt1+2:r+t1+t2, …, Xt1+r:r+t1+t2 by trimming the t1 smallest and the t2 largest from the conceptual sample. This modification is called the r-th trimmed L-moment (TL-moment) and is marked
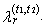 Thus, TL-moment of the r-th order of random variable X is defined
Thus, TL-moment of the r-th order of random variable X is defined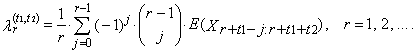 | (30) |
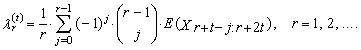 | (31) |
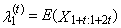 is the expected value of median from conceptual random sample of sample size 1 + 2t. It is necessary here to note that
is the expected value of median from conceptual random sample of sample size 1 + 2t. It is necessary here to note that 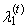 is equal to zero for distributions, which are symmetrical around zero.First four TL-moments have the form for t = 1
is equal to zero for distributions, which are symmetrical around zero.First four TL-moments have the form for t = 1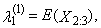 | (32) |
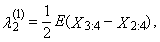 | (33) |
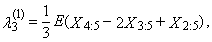 | (34) |
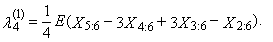 | (35) |
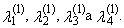 The expected value E(Xr:n) can be written using the formula (2). Using equation (2) we can re-express the right side of equation (31)
The expected value E(Xr:n) can be written using the formula (2). Using equation (2) we can re-express the right side of equation (31)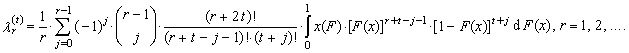 | (36) |
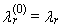 is a normal the r-th L-moment without any trimming.Expressions (32)-(35) for the first four TL-moments, where t = 1, can be written in an alternative manner
is a normal the r-th L-moment without any trimming.Expressions (32)-(35) for the first four TL-moments, where t = 1, can be written in an alternative manner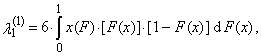 | (37) |
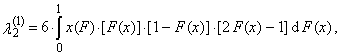 | (38) |
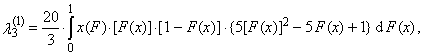 | (39) |
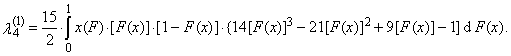 | (40) |
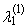 (the expected value of median of conceptual random sample of sample size three) exists for Cauchy’s distribution, although the first L-moment λ1 does not exist.TL-skewness
(the expected value of median of conceptual random sample of sample size three) exists for Cauchy’s distribution, although the first L-moment λ1 does not exist.TL-skewness 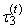 and TL-kurtosis
and TL-kurtosis 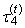 are defined analogously as L-skewness
are defined analogously as L-skewness 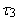 and L-kurtosis
and L-kurtosis 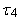
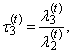 | (41) |
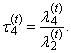 | (42) |
3.2. Sample TL-Moments
- Let x1, x2, …, xn is a sample and
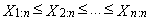 is an ordered sample. Expression
is an ordered sample. Expression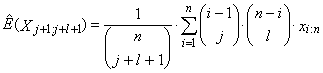 | (43) |
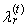 in (31)
in (31) 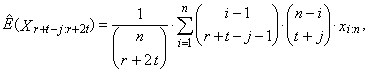 | (44) |
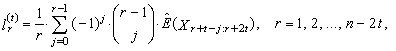 | (45) |
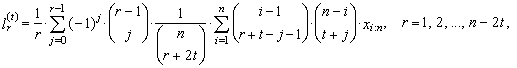 | (46) |
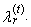 Note that for each j = 0, 1, …, r − 1, values xi:n in (46) are nonzero only for r + t – j ≤ i ≤ n – t −j due to the combinatorial numbers. Simple adjustment of the equation (46) provides an alternative linear form
Note that for each j = 0, 1, …, r − 1, values xi:n in (46) are nonzero only for r + t – j ≤ i ≤ n – t −j due to the combinatorial numbers. Simple adjustment of the equation (46) provides an alternative linear form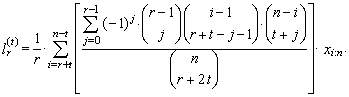 | (47) |
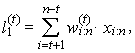 | (48) |
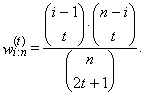 | (49) |
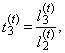 | (50) |
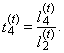 | (51) |
|
4. Lognormal Curves
4.1. Three-Parametric Lognormal Curves
- Random variable X has three-parametric lognormal distribution with parameters µ, σ2 and θ, where –∞ < µ < ∞, σ2 > 0, –∞ < θ < ∞, if its probability density function have the form
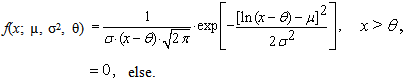 | (52) |
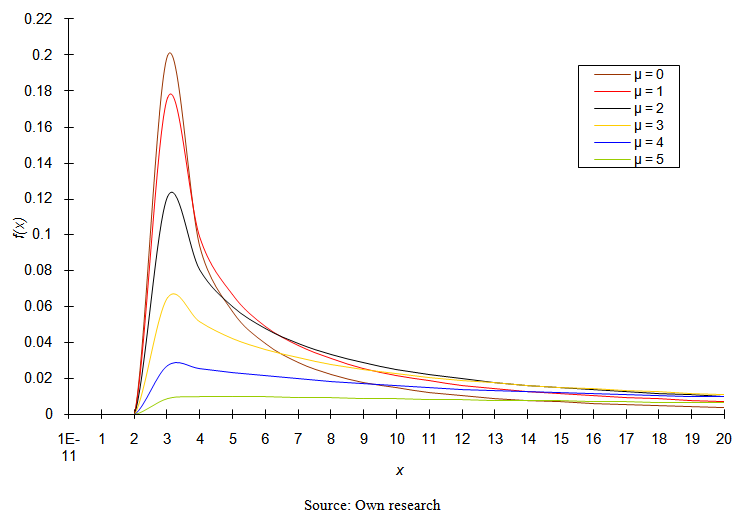 | Figure 1. Probability density function of three-parametric lognormal distribution for the values of parameters σ = 2 (σ2 = 4); θ = 2 |
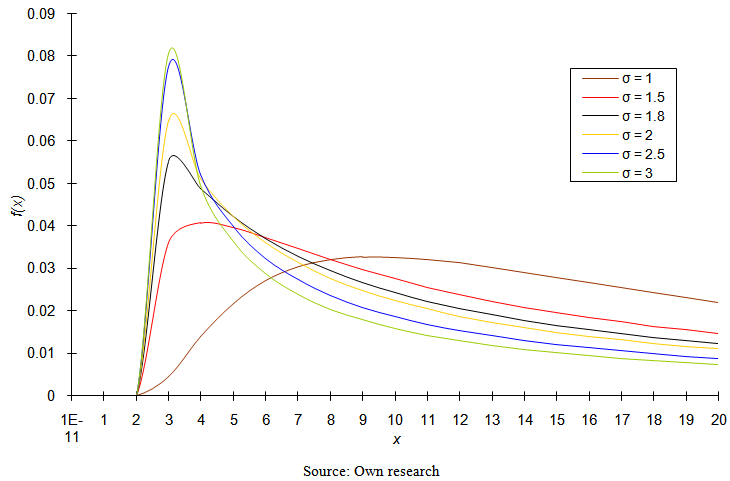 | Figure 2. Probability density function of three-parametric lognormal distribution for the values of parameters μ = 3; θ = 2 |
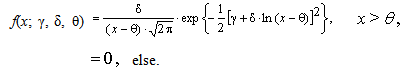 | (53) |
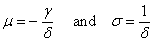 between the expressions for probability density functions (52) and (53).If we substitute θ = 0 (distribution minimum) into expressions for the probability density function of three-parametric lognormal distribution (52) and (53), we obtain formulas for the probability density function of two-parametric lognormal distribution.Distribution function of three-parametric lognormal distribution has the form
between the expressions for probability density functions (52) and (53).If we substitute θ = 0 (distribution minimum) into expressions for the probability density function of three-parametric lognormal distribution (52) and (53), we obtain formulas for the probability density function of two-parametric lognormal distribution.Distribution function of three-parametric lognormal distribution has the form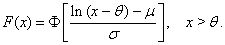 | (54) |
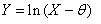 | (55) |
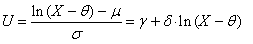 | (56) |
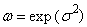 the r-th common and central moments of three-parametric lognormal distribution have the form
the r-th common and central moments of three-parametric lognormal distribution have the form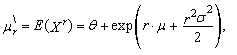 | (57) |
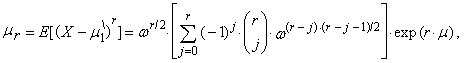 | (58) |
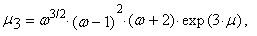 | (59) |
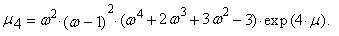 | (60) |
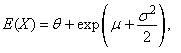 | (61) |
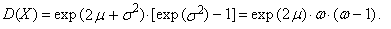 | (62) |
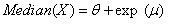 | (63) |
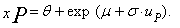 | (64) |
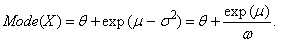 | (65) |
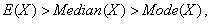 | (66) |
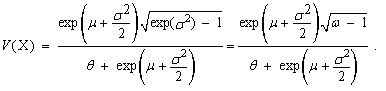 | (67) |
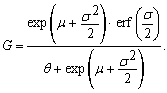 | (68) |
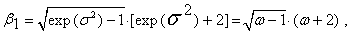 | (69) |
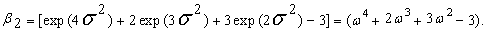 | (70) |
4.2. Four-Parametric Lognormal Curves
- Random variable X has four-parametric lognormal distribution with parameters µ, σ2, θ a τ, where –∞ < µ < ∞, σ2 > 0, –∞ < θ < τ < ∞, if its probability density function has the form
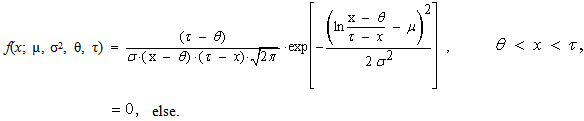 | (71) |
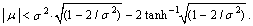
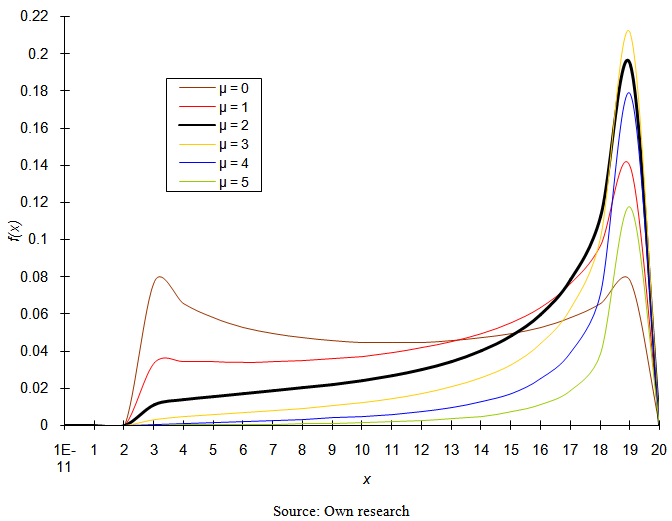 | Figure 3. Probability density function of four-parametric lognormal distribution for the values of parameters σ = 2 (σ2 = 4); θ = 2; τ = 20 |
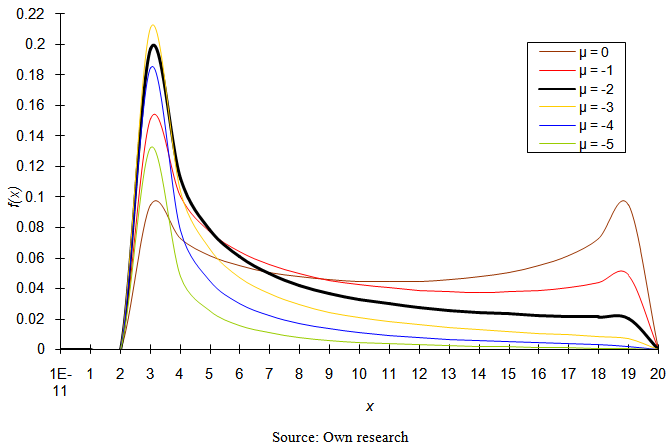 | Figure 4. Probability density function of four-parametric lognormal distribution for the values of parameters σ = 2 (σ2 = 4); θ = 2; τ = 20 |
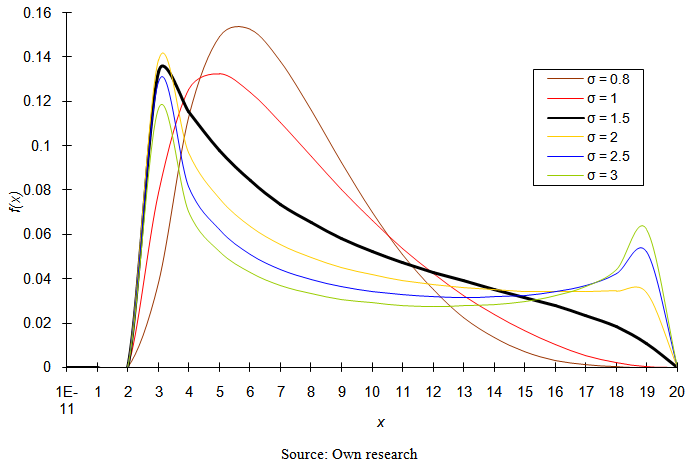 | Figure 5. Probability density function of four-parametric lognormal distribution for the values of parameters μ = –1; θ = 2; τ = 20 |
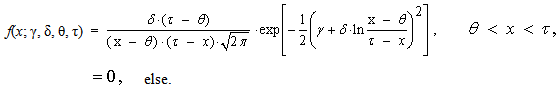 | (72) |
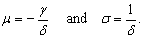 If the random variable X has four-parametric lognormal distribution LN(µ, σ2, θ, τ), then the random variable
If the random variable X has four-parametric lognormal distribution LN(µ, σ2, θ, τ), then the random variable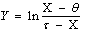 | (73) |
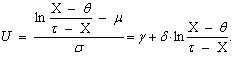 | (74) |
5. Methods of Parameter Estimation
- We focus here only on the parameter estimation of three-parametric lognormal distribution, which is the basic theoretical probability distribution of this research. Various methods of parametric estimation can be used for estimating the parameters of three-parametric lognormal distribution. There are for example the maximum likelihood method, moment method, quantile method, Kemsley’s method, Cohen’s method, L-moment method, TL-moment method, graphical method, etc. We focus on maximum likelihood method and on lesser-known methods of parametric estimation, i.e. Kemsley’s method and Cohen’s method.
5.1. Maximum Likelihood Method
- Let the random sample of the sample size n comes from three-parametric lognormal distribution with probability density function (52) or (53). Then the likelihood function has the form
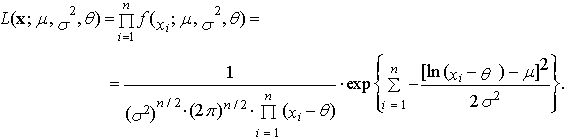 | (75) |
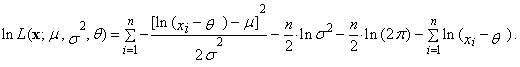 | (76) |
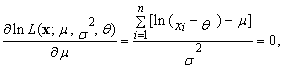 | (77) |
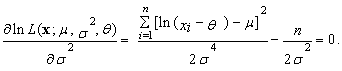 | (78) |
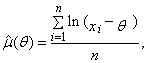 | (79) |
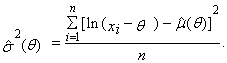 | (80) |
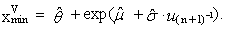 | (81) |
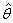 satisfying the equation
satisfying the equation 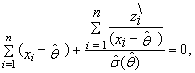 | (82) |
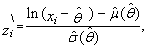 | (83) |
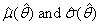 satisfy equations (79) and (80) with the parameter θ replaced by
satisfy equations (79) and (80) with the parameter θ replaced by 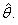 We may also obtain the limits of variances
We may also obtain the limits of variances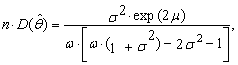 | (84) |
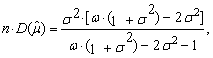 | (85) |
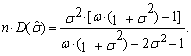 | (86) |
5.2. Kemsley’s Method
- Kemsley used the estimation method, which is a combination of moment and quantile methods of parametric estimation. This method of parametric estimation put into equality the sample quantiles
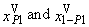 and the corresponding theoretical quantiles of the probability distribution. We get the last equation so that we put sample average equal to the expected value of the probability distribution (“K” means Kemsley’s estimation).
and the corresponding theoretical quantiles of the probability distribution. We get the last equation so that we put sample average equal to the expected value of the probability distribution (“K” means Kemsley’s estimation). 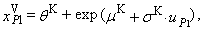 | (87) |
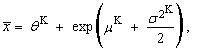 | (88) |
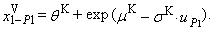 | (89) |
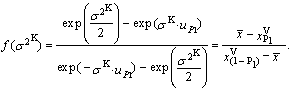 | (90) |
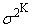 determines approximately using Figure 6. Then we obtain the values of the remaining two parameters using the expressions
determines approximately using Figure 6. Then we obtain the values of the remaining two parameters using the expressions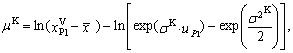 | (91) |
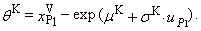 | (92) |
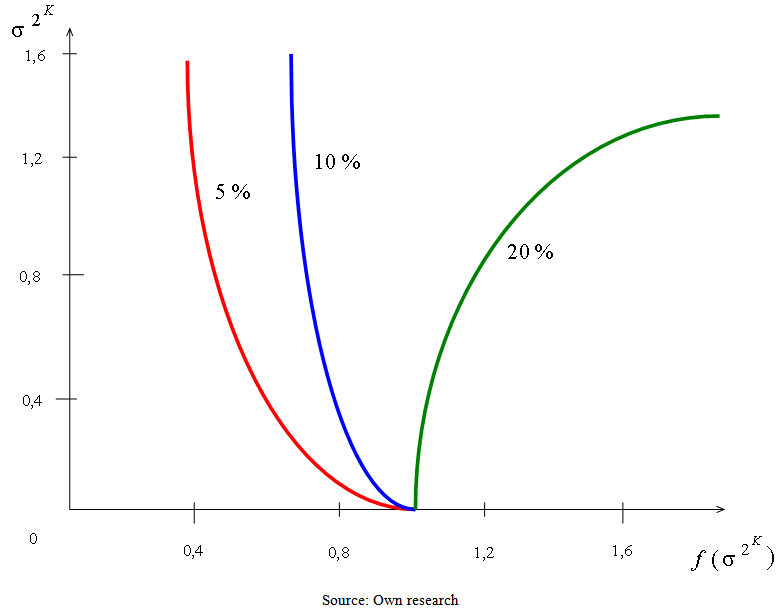 | Figure 6. Graph 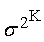 for Kemsley’s method of parametric estimation for p1 = 0,05; 0,10 and 0,20 for Kemsley’s method of parametric estimation for p1 = 0,05; 0,10 and 0,20 |
5.3. Cohen’s Method of the Smallest Sample Value
- It is known that parameter θ determines the beginning of three-parametric lognormal distribution. In this case, an appropriate estimation would be a function of the smallest sample value. This method constitutes an alternative to the method of maximum likelihood. This keeps the equations (79) and (80) and needed the third equation is based on the smallest sample value xmin. If the value xmin is contained nmin-times in the sample, then the sample quantile of order nmin/n in the third equation is putted into equality to the corresponding theoretical quantile of the distribution. Thus, Cohen’s method represents a combination of maximum likelihood method and the quantile method. We can get the parameter estimations obtained by Cohen’s method with the system of equations (“C” means Cohen’s estimation)
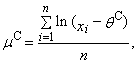 | (93) |
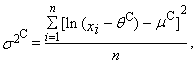 | (94) |
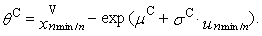 | (95) |
6. Appropriateness of the Model
- It is also necessary to assess the suitability of constructed model or choose a model from several alternatives, which is made by some criterion, which can be a sum of absolute deviations of the observed and theoretical frequencies for all intervals
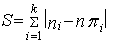 | (96) |
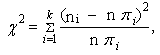 | (97) |
 because in goodness of fit tests in the case of wage distribution we meet frequently with the fact that we work with large sample sizes and therefore the tests would almost always lead to the rejection of the null hypothesis. This results not only from the fact that with such large sample sizes the power of the test is so high at the chosen significance level that the test uncovers all the slightest deviations of the actual wage distribution and a model, but it also results from the principle of construction of the test. But practically we are not interested in such small deviations, so only gross agreement of the model with reality is sufficient and we so called “borrow” the model (curve). Test criterion χ2 can be used in that direction only tentatively. When evaluating the suitability of the model we proceed to a large extent subjective and we rely on experience and logical analysis.
because in goodness of fit tests in the case of wage distribution we meet frequently with the fact that we work with large sample sizes and therefore the tests would almost always lead to the rejection of the null hypothesis. This results not only from the fact that with such large sample sizes the power of the test is so high at the chosen significance level that the test uncovers all the slightest deviations of the actual wage distribution and a model, but it also results from the principle of construction of the test. But practically we are not interested in such small deviations, so only gross agreement of the model with reality is sufficient and we so called “borrow” the model (curve). Test criterion χ2 can be used in that direction only tentatively. When evaluating the suitability of the model we proceed to a large extent subjective and we rely on experience and logical analysis.7. Database
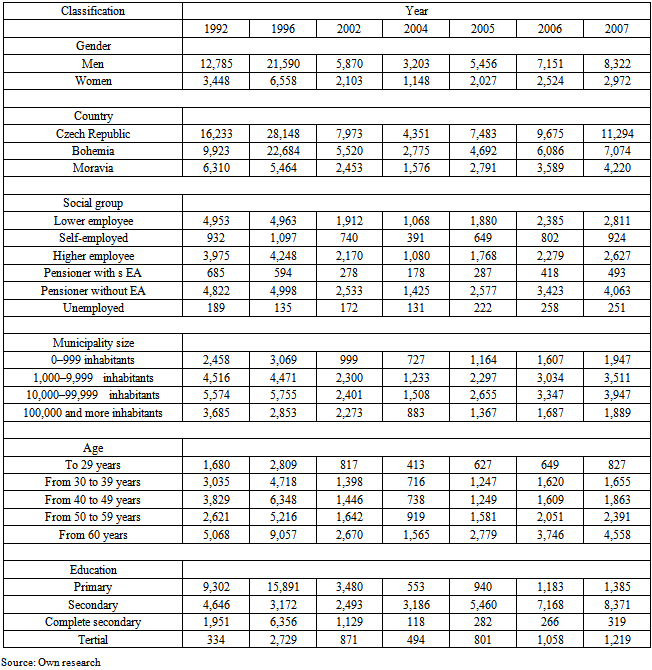
- In the past L-moments were mainly used in hydrology, climatology and meteorology in the research of extreme precipitation, see for example [14]. There are mainly small data sets in this case. This study presents an application of L-moments and TL-moments on large sets of economic data, Table 4 presents the sample sizes of obtained sample sets of households.
|
 | Figure 7. Map of the Czech republic (Bohemia and Moravia) |
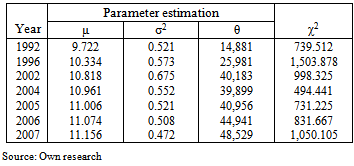
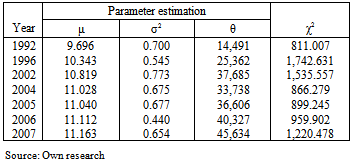
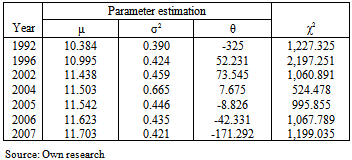
8. Results and Discussion
- Method of TL-moments provided the most accurate results in almost all cases, with the negligible exceptions. Method of L-moments results as the second in more than half of the cases, although the differences between the method of L-moments and maximum likelihood method are not distinctive enough to turn in the number of cases where the method of L-moments came out better than maximum likelihood method. Tables 5–7 are the typical representative of the results for all 168 income distributions. These tables provide the results for the total household set in the Czech Republic. They contain the estimated values of the parameters of three-parametric lognormal distribution, which were obtained simultaneously using the method of TL-moments, method of L-moments and maximum likelihood method, and the value of test criterion (97). This is evident from the values of the criterion that the method of L-moments brought more accurate results than maximum likelihood method in four of seven cases. The most accurate results were obtained using the method of TL-moments in all seven cases.
|
|
|
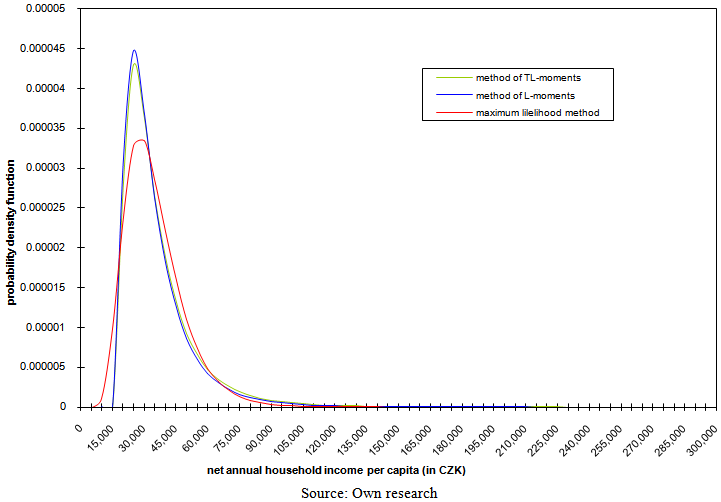 | Figure 8. Model probability density functions of three-parametric lognormal curves in 1992 with parameters estimated using three various robust methods of point parameter estimation |
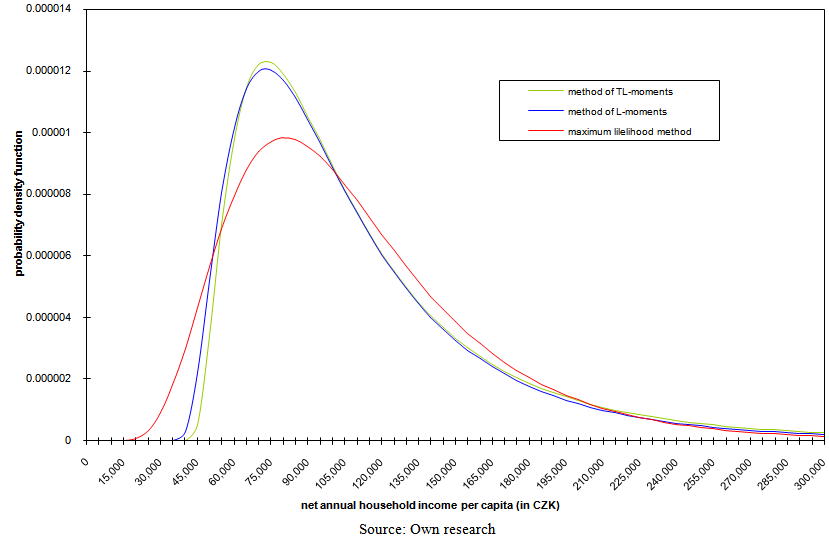 | Figure 9. Model probability density functions of three-parametric lognormal curves in 2004 with parameters estimated using three various robust methods of point parameter estimation |
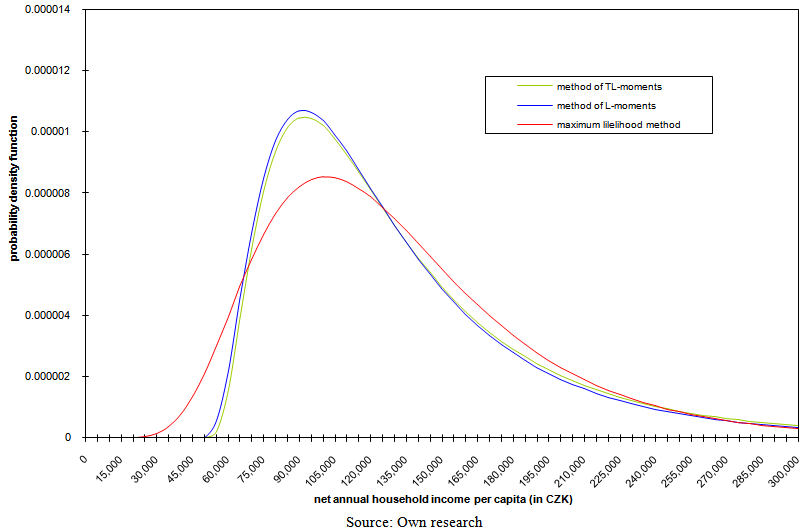 | Figure 10. Model probability density functions of three-parametric lognormal curves in 2007 with parameters estimated using three various robust methods of point parameter estimation |
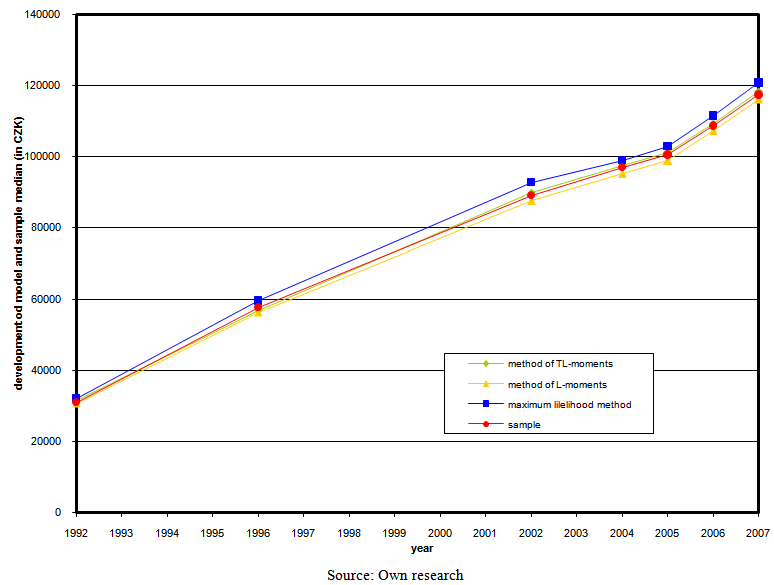 | Figure 11. Development of model and sample median of net annual household income per capita (in CZK) |
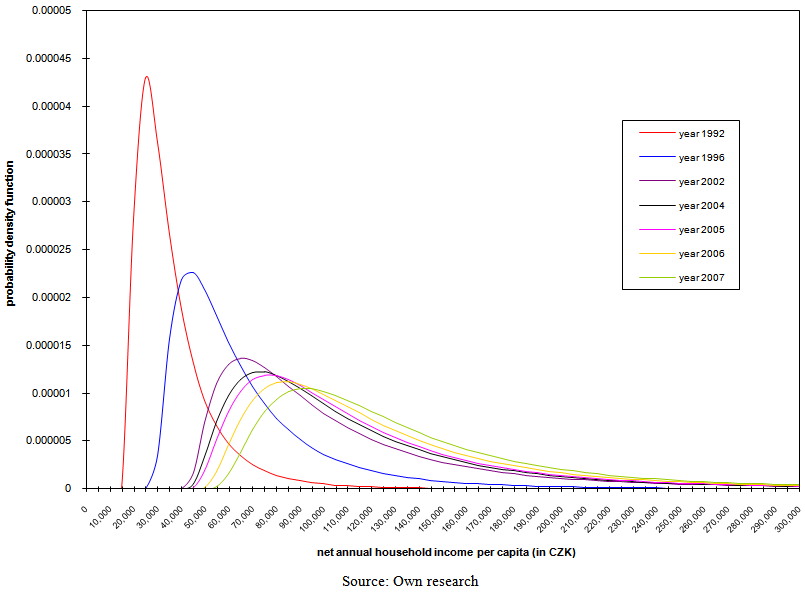 | Figure 12. Development of probability density function of three-parameter lognormal curves with parameters estimated using the method of TL-moments |
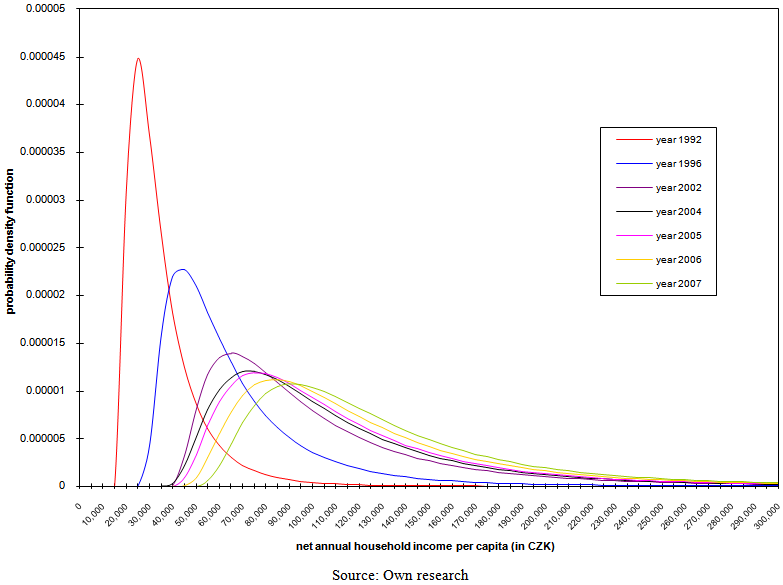 | Figure 13. Development of probability density function of three-parameter lognormal curves with parameters estimated using the method of L-moments |
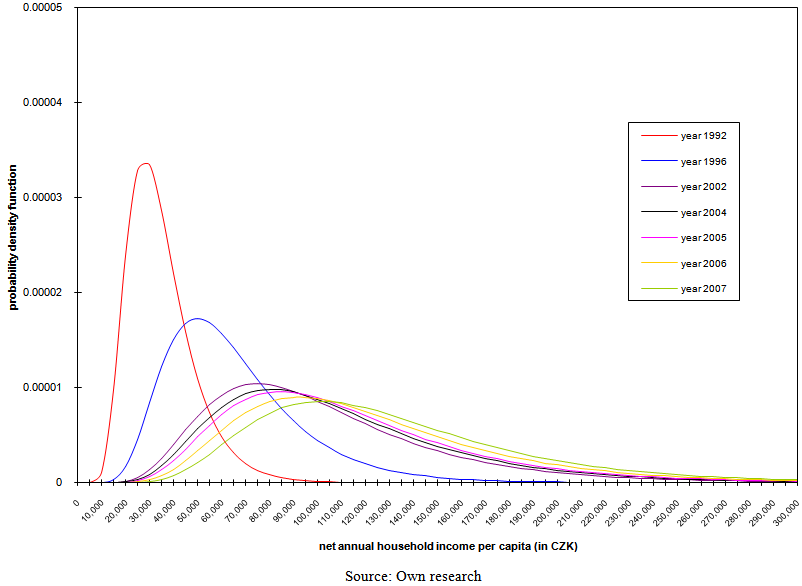 | Figure 14. Development of probability density function of three-parameter lognormal curves with parameters estimated using the maximum likelihood method |
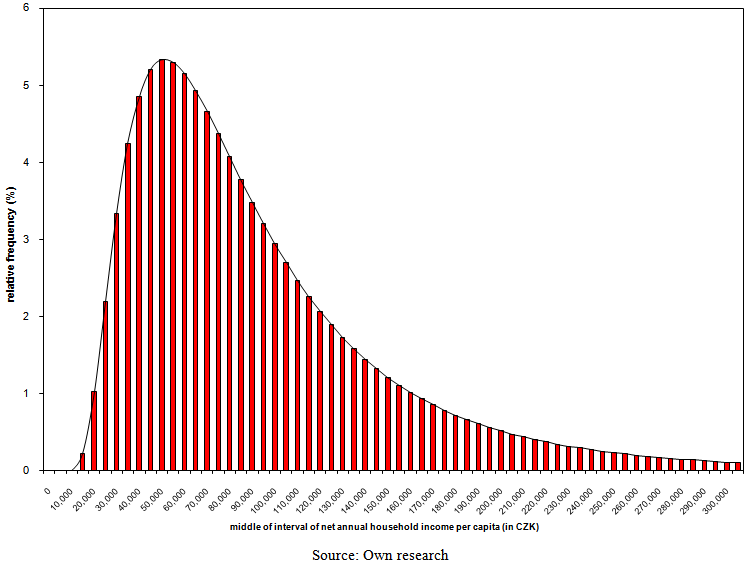 | Figure 15. Model ratios of employees by the band of net annual household income per capita with parameters of three-parametric lognormal curves estimated by the method of TL-moments in 2007 |
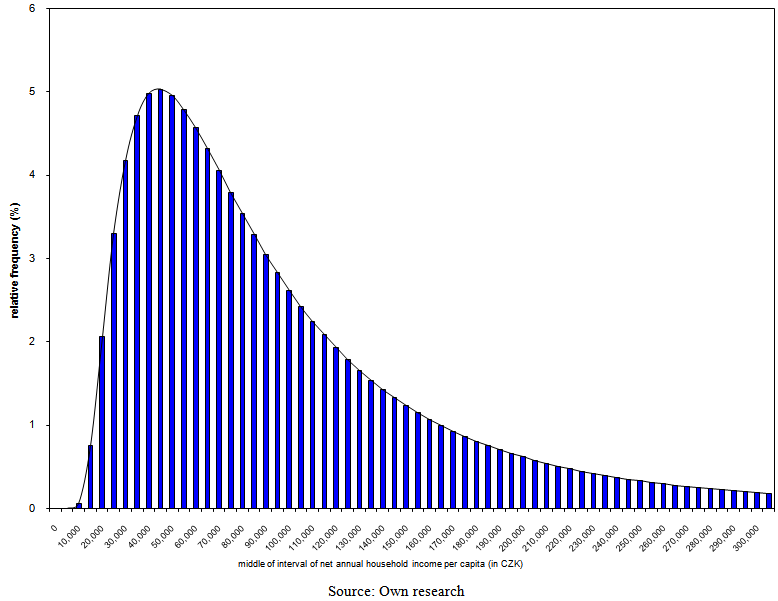 | Figure 16. Model ratios of employees by the band of net annual household income per capita with parameters of three-parametric lognormal curves estimated by the method of L-moments in 2007 |
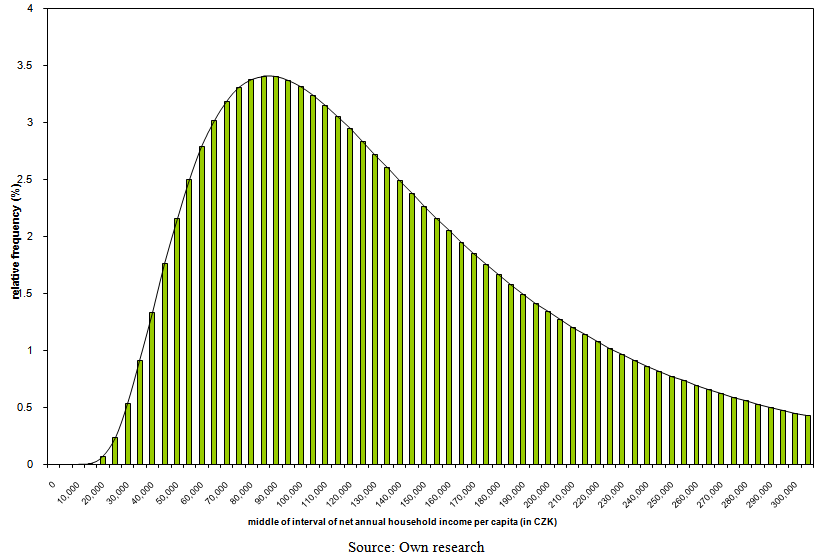 | Figure 17. Model ratios of employees by the band of net annual household income per capita with parameters of three-parametric lognormal curves estimated by the maximum likelihood method in 2007 |
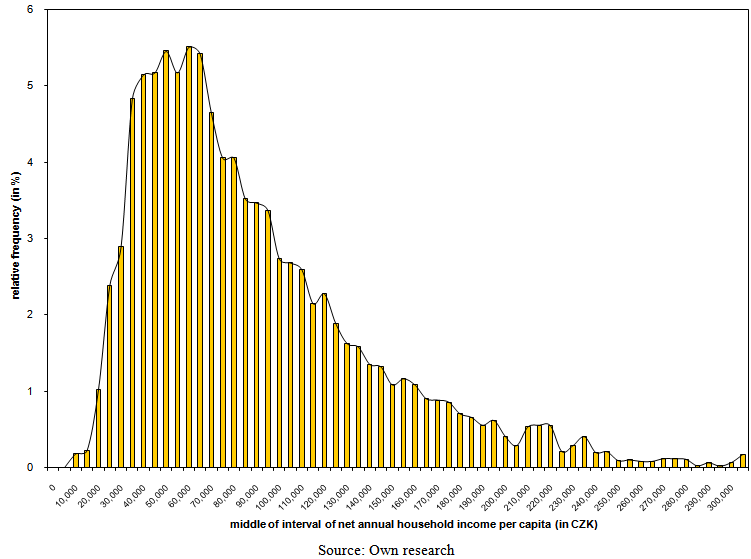 | Figure 18. Sample ratios of employees by the band of net annual household income per capita in 2007 |
9. Conclusions
- Relatively new class of moment characteristics of probability distributions were here introduced. There are the characteristics of location (level), variability, skewness and kurtosis of probability distributions constructed using L-moments and TL-moments that are robust extension of L-moments. Own L-moments have been introduced as a robust alternative to classical moments of probability distributions. However, L-moments and their estimations lack some robust features that belong to TL-moments.Sample TL-moments are linear combinations of the sample order statistics, which assign zero weight to a predetermined number of sample outliers. Sample TL-moments are unbiased estimations of the corresponding TL-moments of probability distributions. Some theoretical and practical aspects of TL-moments are still the subject of research or they remain for future research. Efficiency of TL-statistics depends on the choice of α, for example,
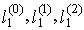 have the smallest variance (the highest efficiency) among other estimations for random samples from normal, logistic and double exponential distribution.The above methods can be also used for modeling the wage distribution or other analysis of economic data (among other methods, see for example [15] or [16]).
have the smallest variance (the highest efficiency) among other estimations for random samples from normal, logistic and double exponential distribution.The above methods can be also used for modeling the wage distribution or other analysis of economic data (among other methods, see for example [15] or [16]).ACKNOWLEDGEMENTS
- This paper was subsidized by the funds of institutional support of a long-term conceptual advancement of science and research number IP400040 at the Faculty of Informatics and Statistics, University of Economics, Prague, Czech Republic.
Notes
- 1) Ix(p, q) is incomplete beta function2) Φ−1(·) is quantile function of standardized normal distribution
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML