Ammar Seddiq Mahmood1, Shukriyah Sabir Ali2
1Department of Mathematics, College of Education, University of Mosul, Iraq
2Department of Mathematics, College of Computers Sciences and Mathematics, University of Mosul, Iraq
Correspondence to: Shukriyah Sabir Ali, Department of Mathematics, College of Computers Sciences and Mathematics, University of Mosul, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Forany partition μ =(μ1, μ2, μ3) of a non - negative integer number r there exist a diagram (A) of β - numbers for each e where e is a positive integer number greater than or equal to two; which introduced by James in 1978. These diagrams (A) play an enormous role in Iwahori-Hecke algebras and q-Schur algebras; as presented by Fayers in 2007. Mahmood gave new diagrams by applying the upside- down application on the main diagram (A) in 2013. Another new diagrams were presented by the authors by applying the direct rotation application on the main diagram (A) in 2013. In the present paper, we introduced some other new diagrams (A1), (A2) and (A3) by employing the composition of upside- down application with direct rotation application of three different degrees namely 90°, 180° and 270° respectively on the main diagram (A). We concluded that we can find the successive main diagrams, (A1), (A2) and (A3) for the guides b2, b3,. . . and be depending on the main diagrams (A1), (A2) and (A3) for b1 and set these facts as rules named Rule (3.1.2), Rule (3.2.2) and Rule (3.3.2) respectively.
Keywords:
β - numbers, Diagram (A), Direct Rotation, Intersection, Partition, Upside-Down
Cite this paper: Ammar Seddiq Mahmood, Shukriyah Sabir Ali, (Upside-Down o Direct Rotation) β - Numbers, American Journal of Mathematics and Statistics, Vol. 4 No. 2, 2014, pp. 58-64. doi: 10.5923/j.ajms.20140402.02.
1. Introduction
Partition theory has a pivotal impact on number theory and has in addition an applied impact on representation theory which is one of the most important elements of modern algebra. This is represented by many studies on this topic, for example [1,3,4]. The present paper deals basically with the subject of representation theory where Young diagram plays an important role in the drafting of the first step of many types of algebras. What benefits us here is (lwahori - Hecke algebras and q-Schur algebras). James (1978), put the new version instead of Young's special diagram of specific composition of positive integer numbers which the sum of them is a non negative integer number called r. He noticed that the new diagram won't work unless the composition is a partition which satisfies the condition (µi ≥ µi+1,∀i) and he called this, Diagram (A). Then he continued putting a new condition when he said there exists e, where e is an integer number greater than or equal to 2. It is according to this number that we will divide the runners of diagram (A). Initially e was taken as a prime integer number, so the results were specific. Fayers (2007), abolished the condition on e being a prime number. Accordingly, the results were too many to give others new scientific capabilities. This subject has a connection with representation theory of lwahori- Hecke algebras and q-Schur algebras [4]. An excellent introduction to the representation theory of Iwahori–Hecke algebras and q-Schur algebras can be found in [3], which also contains the definition of integer partition. More detail on the latter and β - numbers was given by James (1978). Counting the β - numbers for any partition 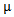 of r requires the definition of an integer b which was showed later by Mohammad (2008), that it must be greater than or equal to the number of parts of
of r requires the definition of an integer b which was showed later by Mohammad (2008), that it must be greater than or equal to the number of parts of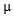 . A. S. Mahmood (2011), introduced the definition of main diagram (s) (A) and the idea of their intersection. S. M. Mahmood (2011), concluded that the conversion of any partition μ of r to diagram (A) of β-numbers makes it easy to identify many properties inherent in the partition much more than putting it in Young diagrams as boxes adjacent to each other. Mahmood (2013), gave new diagrams by applying the upside-down application on the main diagram (A). Other new diagrams were presented by the authors (2013), by applying the direct rotation application on the main diagram (A). In the present paper, we think of introducing other diagrams by employing the composition of the application in [8] with the application in [9] on the main diagram (A). The following questions were posed:1. Can we find the new partition from the old one directly?2. Is the movement of the beads in the new main diagrams regular or not ? If it is regular, can we design the new main diagrams for the guides b2, b3, . . ., and be depending on the new main diagram for b1 ?3. Is there any relation between the intersection of the diagrams in the normal case and the new case ?To answer these questions, the paper is organized as follows. In section two, we suggest the background and notations. In section three, we put forth the new diagrams of (upside-down o direct rotation β-numbers. In section four, we summarize the rules for designing the new main diagrams for the guides b2,b3,. . ., and be depending on the new main diagram for b1.
. A. S. Mahmood (2011), introduced the definition of main diagram (s) (A) and the idea of their intersection. S. M. Mahmood (2011), concluded that the conversion of any partition μ of r to diagram (A) of β-numbers makes it easy to identify many properties inherent in the partition much more than putting it in Young diagrams as boxes adjacent to each other. Mahmood (2013), gave new diagrams by applying the upside-down application on the main diagram (A). Other new diagrams were presented by the authors (2013), by applying the direct rotation application on the main diagram (A). In the present paper, we think of introducing other diagrams by employing the composition of the application in [8] with the application in [9] on the main diagram (A). The following questions were posed:1. Can we find the new partition from the old one directly?2. Is the movement of the beads in the new main diagrams regular or not ? If it is regular, can we design the new main diagrams for the guides b2, b3, . . ., and be depending on the new main diagram for b1 ?3. Is there any relation between the intersection of the diagrams in the normal case and the new case ?To answer these questions, the paper is organized as follows. In section two, we suggest the background and notations. In section three, we put forth the new diagrams of (upside-down o direct rotation β-numbers. In section four, we summarize the rules for designing the new main diagrams for the guides b2,b3,. . ., and be depending on the new main diagram for b1.
2. Background and Notations
2.1. Diagram (A) of β-Numbers
Let r be a non-negative integer, A partition 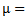
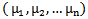 of r is a sequence of non - negative integers such that
of r is a sequence of non - negative integers such that 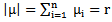 and
and 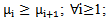 [3]. For example,
[3]. For example, 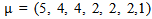 is a partition of r =20. β-numbers was defined by; see James in [2]: "Fix
is a partition of r =20. β-numbers was defined by; see James in [2]: "Fix 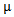 is a partition of r, choose an integer b greater than or equal to the number of parts of
is a partition of r, choose an integer b greater than or equal to the number of parts of 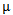 and define
and define 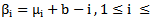
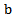 . The set { β1, β2,..., βb } is said to be the set of β -numbers for
. The set { β1, β2,..., βb } is said to be the set of β -numbers for 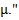 For the above example, if we take b =7, then the set of β-numbers is{11, 9, 8,5,4, 3,1}.Now, let e be a positive integer number greater than or equal to 2, we can represent β - numbers by a diagram called diagram (A).
For the above example, if we take b =7, then the set of β-numbers is{11, 9, 8,5,4, 3,1}.Now, let e be a positive integer number greater than or equal to 2, we can represent β - numbers by a diagram called diagram (A). Where every β will be represented by a bead ( ● ) which takes its location in diagram (A). Returning to the above example, diagram (A) of β -numbers for e =2 and e =3 is as shown below in diagram 1 and 2 respectively:
Where every β will be represented by a bead ( ● ) which takes its location in diagram (A). Returning to the above example, diagram (A) of β -numbers for e =2 and e =3 is as shown below in diagram 1 and 2 respectively: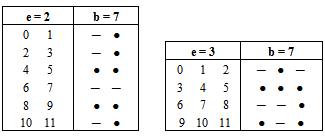 Diagram 1.
Diagram 1.  Diagram 2.Note: Throughout this paper, e denotes a fixed integer greater than or equal to 2. we mean by diagram (A); diagram (A) of β-numbers.
Diagram 2.Note: Throughout this paper, e denotes a fixed integer greater than or equal to 2. we mean by diagram (A); diagram (A) of β-numbers.
2.2. The Main Diagrams (A)
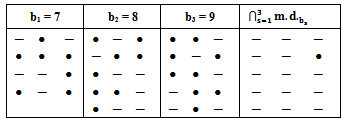
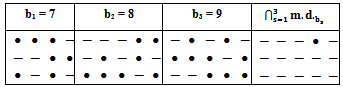
Mahmood in [6] introduced the definition of main diagram(s) (A) and the idea of the intersection of these main diagrams. in the following subsections, we repeat the principals results, as follows: Since the value of b ≥ n; [5], then we deal with an infinite numbers of values of b. Here we want to mention that for each value of b there is a special diagram (A) of β - numbers for it, but there is a repeated part of one's diagram with the other values of b where a "Down –shifted" or "Up- shifted", occurs when we take the following:(b1 if b = n), (b2 if b = n+1), . . . and (be if b = n+(e-1)).Definition (2.2.1.): [6] The values of b1, b2, . . . and be are called the guides of any diagram (A) of β-numbers.From the above example where 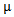 = (5, 4, 4, 2, 2, 2,1), r = 20, if e = 2 then there are two guides, the first is b1 = 7 since n = 7 and the second is b2 = 8, the β - numbers are given in table 1:
= (5, 4, 4, 2, 2, 2,1), r = 20, if e = 2 then there are two guides, the first is b1 = 7 since n = 7 and the second is b2 = 8, the β - numbers are given in table 1:Table 1. β- Numbers
 |
| |
|
We define any diagram (A) that corresponds any b guides as a "main diagram" or "guide diagram".Theorem (2.2.2.): [6] There is e of main diagrams for any partition  of r.Hence, for our example, we have two main diagrams for e=2 as shown in diagram 3:
of r.Hence, for our example, we have two main diagrams for e=2 as shown in diagram 3: 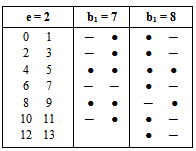 | Diagram 3. |
And the idea of "Down –shifted" or "Up- shifted", is declared in diagram 4 below: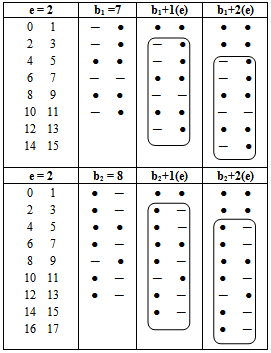 | Diagram 4. Illustrates the Idea of "Down- shifted" |
2.3. Some Kinds of Partition
Any partition 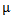 of r is called w-regular; w ≥ 2, if there does not exist i ≥ 1 such that
of r is called w-regular; w ≥ 2, if there does not exist i ≥ 1 such that 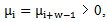 and
and 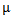 is called w-restricted if
is called w-restricted if 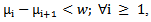 [3].From the above example, where
[3].From the above example, where 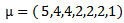 then
then 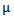 is 4-regular and 3-restricted.
is 4-regular and 3-restricted.
2.4. The Intersection of the Main Diagrams
The idea of the intersection of any main diagrams is defined by the following:1. Let τ be the number of redundant part of the partition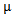 of r, then we have:
of r, then we have: 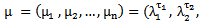
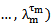 such that
such that 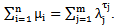 2. We denote the intersection of main diagrams by
2. We denote the intersection of main diagrams by 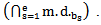 3. The intersection result as a numerical value will be denoted by
3. The intersection result as a numerical value will be denoted by 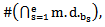 and it is equal to
and it is equal to 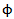 in the case of no existence of any bead, or γ in the case that γ common beads exist in the main diagrams.For our example, the intersection of the two main diagrams is as shown in diagram 5:
in the case of no existence of any bead, or γ in the case that γ common beads exist in the main diagrams.For our example, the intersection of the two main diagrams is as shown in diagram 5: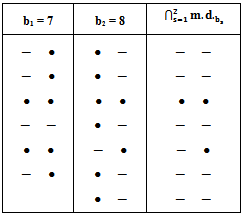 | Diagram 5. |
Notice that, 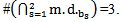 The two principle theorems about the idea of the intersection of any main diagrams are:Theorem (2.4.1.): [6] For any e ≥ 2, the following holds:1-
The two principle theorems about the idea of the intersection of any main diagrams are:Theorem (2.4.1.): [6] For any e ≥ 2, the following holds:1- 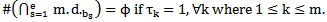 2- Let
2- Let 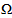 be the number of parts of
be the number of parts of 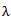 which satisfies the condition
which satisfies the condition 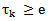 for some k, then:
for some k, then: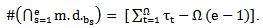 Theorem (2.4.2.): [6]1- Let
Theorem (2.4.2.): [6]1- Let 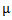 be a partition of r and
be a partition of r and 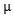 is w-regular, then:
is w-regular, then: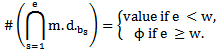 2- Let
2- Let 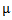 be a partition of r and
be a partition of r and 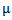 is h-restricted, then:
is h-restricted, then: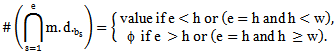 Also, S. M. Mahmood in [7] gave the same subject by using a new technique which supported the results of Mahmood in [6].
Also, S. M. Mahmood in [7] gave the same subject by using a new technique which supported the results of Mahmood in [6].
3. (Upside-Down o Direct Rotation) β - Numbers
In the present paper, we introduce some new diagrams depending on the old diagram (A) by employing the composition of upside-down application with direct rotation application of three different degrees namely 90o, 180o and 270o respectively .As a preliminary step toward the subject, we give the following notations:1. By direct rotation; we mean: counter clockwise rotation. 2. All the rotations are about the origin. 3. Composition is the combination of two or more mappings to form a single new mapping. Here, we remind with the definition of composition of two mappings: Let f : S → T and g: T → U be two mappings. We define the composition of f followed by g, denoted by g ο f, to be the mapping (g ο f)(x) = g (f (x)), for all x ∈ S.Note carefully that in the notation (g ο f ) the mapping on the right is applied first. See figure 1.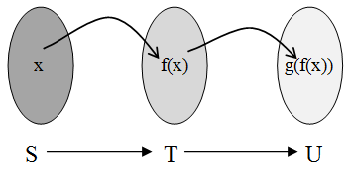 | Figure 1. |
4. The new diagrams created by the composition application have another partitions of the origin partition and if we use the idea of the intersection, the partition of the beads will not be the same (or will not be the sum) in 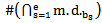 in the normal main diagrams.To realize these facts, we study the composition application for each degree apart on the previous example where
in the normal main diagrams.To realize these facts, we study the composition application for each degree apart on the previous example where 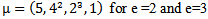 as follows:
as follows:
3.1. (Upside-Down o Direct Rotation of degree 90o) β - Numbers
The diagrams introduced by this application is denoted by (A1) and are shown in diagram 6.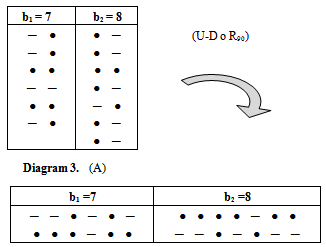 | Diagram 6. (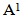 ) ) |
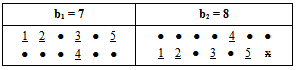
Now, if we use the old technique for finding any partition of any diagram (A1), the value of the partition will not be equal to the origin partition? so, we delete any effect of (-) in (A) after the position of β1, and we start with number 1 for the first (-) a (left to right) in any row exist in (A), and with number 2 for the second (-) and ..., etc, and we stop with last (-) before the position β1 in (A) as shown in diagram 7. Now, to apply "upside-down o direct rotation of degree 90o" on (A), the new version (A1) has the same partition of (A), see diagram 8.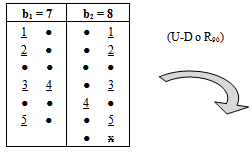 | Diagram 7. (A) |
 | Diagram 8. ( ) ) |
Remark (3.1.1.): The main diagram (A1) in case b1 = n, plays a main role to design all the main diagrams (A1) for (b2 = n+1), ... and (be= n+(e-1)), as follows:Rule (3.1.2.): Since the main diagram (A1) in the case b1, we can find the successive main diagrams (A1) for b2, b3, ... and be , as follows:1. 1st row in the case 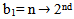 row in the case b2 and to one
row in the case b2 and to one 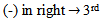 row in the case b3 and to add one (-) in right
row in the case b3 and to add one (-) in right  last row in the case be and to add one (-) in right of main diagram (A1).2. 2nd row in the case
last row in the case be and to add one (-) in right of main diagram (A1).2. 2nd row in the case 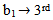 row in the case b2 and to add one (-) in right
row in the case b2 and to add one (-) in right  last row in the case be-1 and to add one
last row in the case be-1 and to add one 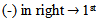 row in the case be and to add one (●) in left.
row in the case be and to add one (●) in left.  e. last row in the case
e. last row in the case 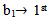 row in the case b2 and to add one (●) in left
row in the case b2 and to add one (●) in left 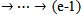 row in the case be and to add one (●) in left. This rule is clarified in diagram 9. For the above example, where
row in the case be and to add one (●) in left. This rule is clarified in diagram 9. For the above example, where 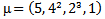 and e = 3.
and e = 3.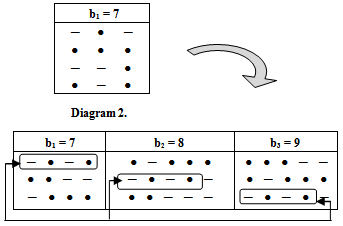 | Diagram 9. |
Theorem (3.1.3.): All the results in [6] about the main diagram (A) is the same of the diagram (A1) but in (upside-down o direct rotation of degree 90o ) position. One of these results is the intersection of the main diagrams. so, the fact mentioned in theorem (3.1.3.) is clear in diagram 10 comparing it with diagram 5, for e = 2 and for e=3, see the two diagrams 11 and 12: | Diagram 10. The intersection of the main diagrams ( ) for e=2 ) for e=2 |
Notice that, 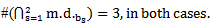
 | Diagram 11. The intersection of the main diagrams (A) for e=3 |
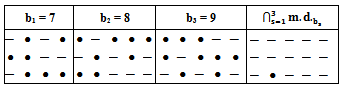 | Diagram 12. The intersection of the main diagrams (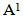 ) for e=3 ) for e=3 |
Notice that, 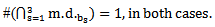
3.2. (Upside-Down o Direct Rotation of degree 180o) β - Numbers
The diagrams introduced by this application is denoted by (A2) and are shown in diagram 13.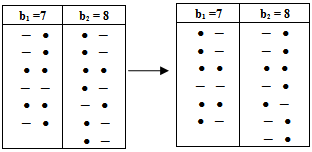 Diagram 3. (A)
Diagram 3. (A)  Diagram 13. (A2)Again, if we use the old technique for finding any partition of any diagram (A2), the value of the partition will not be equal to the origin partition? so, we delete any effect of (-) in (A) after the position of β1, and we start with number 1 for the first (-) a (left to right) in any row exist in (A), and with number 2 for the second (-) and ..., etc, and we stop with last (-) before the position β1 in (A) as shown in diagram 7. Now, to apply "upside-down o Direct rotation of degree 1805 " on (A), the new version (A2) has the same partition of (A), see diagram 14.
Diagram 13. (A2)Again, if we use the old technique for finding any partition of any diagram (A2), the value of the partition will not be equal to the origin partition? so, we delete any effect of (-) in (A) after the position of β1, and we start with number 1 for the first (-) a (left to right) in any row exist in (A), and with number 2 for the second (-) and ..., etc, and we stop with last (-) before the position β1 in (A) as shown in diagram 7. Now, to apply "upside-down o Direct rotation of degree 1805 " on (A), the new version (A2) has the same partition of (A), see diagram 14.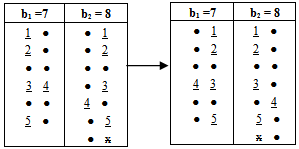 Diagram 7. (A)
Diagram 7. (A)  Diagram 14. (A2)Remark(3.2.1.): The main diagram (A2) in case b1 = n, plays a main role to design all the main diagrams (A2) for (b2 = n+1), ... and (be= n+(e-1)), as follows:Rule (3.2.2.): Since the main diagram (A2) in the case b1, we can find the successive main diagrams (A2) for b2, b3, ... and be , as follows:1. 1st column in the case
Diagram 14. (A2)Remark(3.2.1.): The main diagram (A2) in case b1 = n, plays a main role to design all the main diagrams (A2) for (b2 = n+1), ... and (be= n+(e-1)), as follows:Rule (3.2.2.): Since the main diagram (A2) in the case b1, we can find the successive main diagrams (A2) for b2, b3, ... and be , as follows:1. 1st column in the case 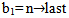 column in the case b2 and to add one (●) in up
column in the case b2 and to add one (●) in up  column in the case b3 and to add one (●) in up
column in the case b3 and to add one (●) in up  column in the case be and to add one (●) in up of main diagram (A2 ).2. 2nd column in the case
column in the case be and to add one (●) in up of main diagram (A2 ).2. 2nd column in the case 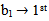 column in the case b2 and to add one (-) in
column in the case b2 and to add one (-) in 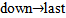 column in the case b3 and to add one (●) in up
column in the case b3 and to add one (●) in up 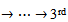 column in the case be and to add one (●) in up.
column in the case be and to add one (●) in up. e. last column in the case
e. last column in the case 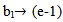 column in the case b2 and to add one (-) in
column in the case b2 and to add one (-) in 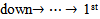 column in the case be and to add one (-) in down. To check this rule For our example, where
column in the case be and to add one (-) in down. To check this rule For our example, where 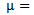
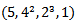 and e = 3, see diagram 15 below:
and e = 3, see diagram 15 below: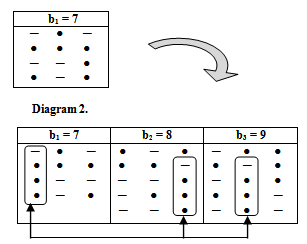 | Diagram 15. |
Theorem (3.2.3.): All the results in [6] about the main diagram (A) is the same of the diagram (A2) but in (upside-down o direct rotation of degree 180o ) position.Now, as we said before, the intersection of the main diagrams is one of these results, hence see diagram 16 and compare it with diagram 5 for e=2 and for e=3, see diagram 17and compare it with diagram 11 above: 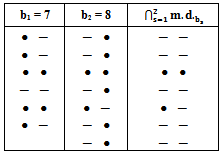 | Diagram 16. The intersection of the main diagrams (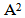 ) for e=2 ) for e=2 |
Again, 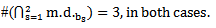
 | Diagram 17. The intersection of the main diagrams (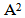 ) for e=3 ) for e=3 |
Also, 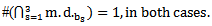
3.3. (Upside-Down o Direct Rotation of Degree 270o) β - Numbers
The diagrams introduced by this application is denoted by (A3) and are shown in diagram 18.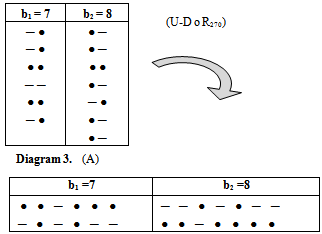 | Diagram 18. (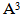 ) ) |
Again, if we use the old technique for finding any partition of any diagram (A3), the value of the partition will not be equal to the origin partition? so, we delete any effect of (-) in (A) after the position of β1, and we start with number 1 for the first (-) a (left to right) in any row exist in (A), and with number 2 for the second (-) and ...,etc, and we stop with last (-) before the position β1 in (A) as shown in diagram 7. Now, to apply "upside-down o Direct rotation of degree 2705 " on (A), the new version (A3) has the same partition of (A), see diagram 19.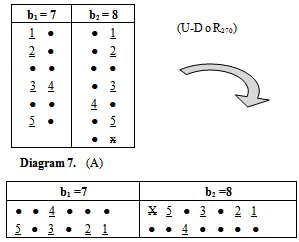 | Diagram 19. (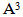 ) ) |
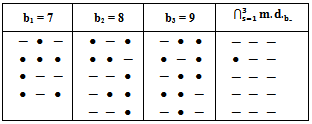
Remark (3.3.1.): The main diagram (A3) in case b1 = n, plays a main role to design all the main diagrams (A3) for (b2 = n+1), ... and (be= n+(e-1)), as follows:Rule (3.3.2): Since the main diagram (A3) in the case b1, we can find the successive main diagrams (A3) for b2, b3, ... and be , as follows:1. 1st row in the case 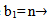 last row in the case b2 and to add one (●) in
last row in the case b2 and to add one (●) in 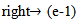 row in the case b3 and to add one (●) in
row in the case b3 and to add one (●) in  row in the case be and to add one (●) in right of main diagram (A3).2. 2nd row in the case
row in the case be and to add one (●) in right of main diagram (A3).2. 2nd row in the case  row in the case b2 and to add one (-) in left
row in the case b2 and to add one (-) in left  row in the cas b3 and to add one (●) in right
row in the cas b3 and to add one (●) in right  row in the case be and to add one (●) in right.
row in the case be and to add one (●) in right. e) last row in the case
e) last row in the case  row in the case b2 and to add one (-) in left
row in the case b2 and to add one (-) in left  row in the case be and to add one (-) in left. To materialize rule (3.3.2) For the our example for e = 3, see diagram 20:
row in the case be and to add one (-) in left. To materialize rule (3.3.2) For the our example for e = 3, see diagram 20: 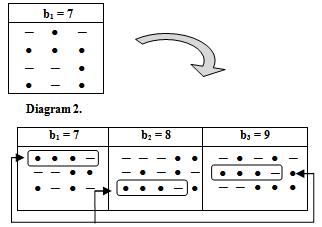 | Diagram 20. |
Theorem (3.3.3.): All the results in [6] about the main diagram (A) is the same of the diagram (A3) but in (upside-down o direct rotation of degree 270o ) position. To perceive theorem (3.3.3.) for this type of rotation, on our example, observe diagrams 21 and compare it with diagram 5 for e=2 and diagram 22 to be compared with diagram 11 for e=3: | Diagram 21. The intersection of the main diagrams ( ) for e=2 ) for e=2 |
Notice that, 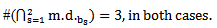
 | Diagram 22. The intersection of the main diagrams (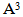 ) for e=3 ) for e=3 |
Also, 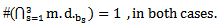
4. Conclusions
1. A procedure is suggested for the diagrams (A1), (A2) and (A3) of β - numbers which they represent the composition of upside - down application with the direct rotation application of degrees 90o, 180o, and 270o respectively, on diagram (A) of β-numbers to have the same partition of diagram (A) of β-numbers.2. Furthermore, for each composition, a rule for designing all the main diagrams of the composition for b2, b3, . . . , and be is set depending on the main diagram of the composition for b1.3. We find out that the intersection of the main diagrams of each composition is the same of the main diagram (A) but in the composition position.4. And finally:a) (Upside-Down o Direct Rotation of degree 90o ) β - Numbers = (Direct Rotation of degree 270o o Upside-Down) β - Numbersb) (Upside-Down o Direct Rotation of degree 180o)
β - Numbers = (Direct Rotation of degree 270o o Upside-Down) β - Numbersb) (Upside-Down o Direct Rotation of degree 180o) β - Numbers = (Direct Rotation of degree 180o o Upside-Down) β - Numbersc) (Upside-Down o Direct Rotation of degree 270o)
β - Numbers = (Direct Rotation of degree 180o o Upside-Down) β - Numbersc) (Upside-Down o Direct Rotation of degree 270o) β - Numbers = (Direct Rotation of degree 90o o Upside-Down) β - Numbers
β - Numbers = (Direct Rotation of degree 90o o Upside-Down) β - Numbers
References
| [1] | George E. Andrews, The Theory of Partitions, Encyclopedia of Mathematics and its Applications, Vol.2, Addison-Wesley publishing company, London, 1976. |
| [2] | G. James, Some combinatorial results involving Young diagrams, Math. Proc. Cambridge Philos. Soc.,83,1-10, 1978. |
| [3] | A. Mathas, Iwahori-Hecke Algebras and Schur Algebras of the Symmetric Groups, Amer. Math. Soc. University Lecture Series, 15, 1999. |
| [4] | M. Fayers, Another runner removal theorem for r- decomposition number of lwahori –Hecke algebras and q- Schur algebras, J. algebra, 310, 396- 404,2007. |
| [5] | H. S. Mohammad, Algorithms of The Core of Algebraic Young's Tableaux, M. Sc. Thesis, College of Education, University of Mosul, 2008. |
| [6] | A. S. Mahmood, On the intersection of Young's diagrams core, J. Education and Science (Mosul University), 24, no. 3, 143- 159, 2011. |
| [7] | S. M. Mahmood, On e- Regular and the Intersection of Young's Diagrams Core, M. Sc. Thesis, College of Education, University of Mosul, 2011. |
| [8] | A. S. Mahmood, Upside - down β - numbers, Australian J. of Basic and Applied Sciences 7, no 7, 986- 990, 2013. |
| [9] | A. S. Mahmood, and Sh. S. Ali, Direct Rotation β- numbers, Journal of Advances in Mathematics, Vol 5, No. 2, 642-650, 2013. |

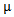 of r requires the definition of an integer b which was showed later by Mohammad (2008), that it must be greater than or equal to the number of parts of
of r requires the definition of an integer b which was showed later by Mohammad (2008), that it must be greater than or equal to the number of parts of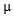 . A. S. Mahmood (2011), introduced the definition of main diagram (s) (A) and the idea of their intersection. S. M. Mahmood (2011), concluded that the conversion of any partition μ of r to diagram (A) of β-numbers makes it easy to identify many properties inherent in the partition much more than putting it in Young diagrams as boxes adjacent to each other. Mahmood (2013), gave new diagrams by applying the upside-down application on the main diagram (A). Other new diagrams were presented by the authors (2013), by applying the direct rotation application on the main diagram (A). In the present paper, we think of introducing other diagrams by employing the composition of the application in [8] with the application in [9] on the main diagram (A). The following questions were posed:1. Can we find the new partition from the old one directly?2. Is the movement of the beads in the new main diagrams regular or not ? If it is regular, can we design the new main diagrams for the guides b2, b3, . . ., and be depending on the new main diagram for b1 ?3. Is there any relation between the intersection of the diagrams in the normal case and the new case ?To answer these questions, the paper is organized as follows. In section two, we suggest the background and notations. In section three, we put forth the new diagrams of (upside-down o direct rotation β-numbers. In section four, we summarize the rules for designing the new main diagrams for the guides b2,b3,. . ., and be depending on the new main diagram for b1.
. A. S. Mahmood (2011), introduced the definition of main diagram (s) (A) and the idea of their intersection. S. M. Mahmood (2011), concluded that the conversion of any partition μ of r to diagram (A) of β-numbers makes it easy to identify many properties inherent in the partition much more than putting it in Young diagrams as boxes adjacent to each other. Mahmood (2013), gave new diagrams by applying the upside-down application on the main diagram (A). Other new diagrams were presented by the authors (2013), by applying the direct rotation application on the main diagram (A). In the present paper, we think of introducing other diagrams by employing the composition of the application in [8] with the application in [9] on the main diagram (A). The following questions were posed:1. Can we find the new partition from the old one directly?2. Is the movement of the beads in the new main diagrams regular or not ? If it is regular, can we design the new main diagrams for the guides b2, b3, . . ., and be depending on the new main diagram for b1 ?3. Is there any relation between the intersection of the diagrams in the normal case and the new case ?To answer these questions, the paper is organized as follows. In section two, we suggest the background and notations. In section three, we put forth the new diagrams of (upside-down o direct rotation β-numbers. In section four, we summarize the rules for designing the new main diagrams for the guides b2,b3,. . ., and be depending on the new main diagram for b1.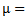
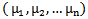 of r is a sequence of non - negative integers such that
of r is a sequence of non - negative integers such that 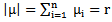 and
and 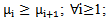 [3]. For example,
[3]. For example, 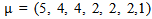 is a partition of r =20. β-numbers was defined by; see James in [2]: "Fix
is a partition of r =20. β-numbers was defined by; see James in [2]: "Fix 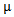 is a partition of r, choose an integer b greater than or equal to the number of parts of
is a partition of r, choose an integer b greater than or equal to the number of parts of 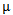 and define
and define 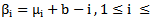
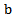 . The set { β1, β2,..., βb } is said to be the set of β -numbers for
. The set { β1, β2,..., βb } is said to be the set of β -numbers for 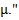 For the above example, if we take b =7, then the set of β-numbers is{11, 9, 8,5,4, 3,1}.Now, let e be a positive integer number greater than or equal to 2, we can represent β - numbers by a diagram called diagram (A).
For the above example, if we take b =7, then the set of β-numbers is{11, 9, 8,5,4, 3,1}.Now, let e be a positive integer number greater than or equal to 2, we can represent β - numbers by a diagram called diagram (A). Where every β will be represented by a bead ( ● ) which takes its location in diagram (A). Returning to the above example, diagram (A) of β -numbers for e =2 and e =3 is as shown below in diagram 1 and 2 respectively:
Where every β will be represented by a bead ( ● ) which takes its location in diagram (A). Returning to the above example, diagram (A) of β -numbers for e =2 and e =3 is as shown below in diagram 1 and 2 respectively: Diagram 1.
Diagram 1.  Diagram 2.Note: Throughout this paper, e denotes a fixed integer greater than or equal to 2. we mean by diagram (A); diagram (A) of β-numbers.
Diagram 2.Note: Throughout this paper, e denotes a fixed integer greater than or equal to 2. we mean by diagram (A); diagram (A) of β-numbers.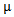 = (5, 4, 4, 2, 2, 2,1), r = 20, if e = 2 then there are two guides, the first is b1 = 7 since n = 7 and the second is b2 = 8, the β - numbers are given in table 1:
= (5, 4, 4, 2, 2, 2,1), r = 20, if e = 2 then there are two guides, the first is b1 = 7 since n = 7 and the second is b2 = 8, the β - numbers are given in table 1: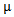 of r.Hence, for our example, we have two main diagrams for e=2 as shown in diagram 3:
of r.Hence, for our example, we have two main diagrams for e=2 as shown in diagram 3: 

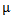 of r is called w-regular; w ≥ 2, if there does not exist i ≥ 1 such that
of r is called w-regular; w ≥ 2, if there does not exist i ≥ 1 such that 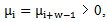 and
and 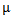 is called w-restricted if
is called w-restricted if 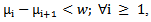 [3].From the above example, where
[3].From the above example, where 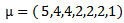 then
then 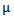 is 4-regular and 3-restricted.
is 4-regular and 3-restricted.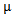 of r, then we have:
of r, then we have: 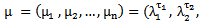
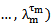 such that
such that 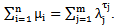 2. We denote the intersection of main diagrams by
2. We denote the intersection of main diagrams by 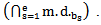 3. The intersection result as a numerical value will be denoted by
3. The intersection result as a numerical value will be denoted by 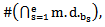 and it is equal to
and it is equal to 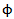 in the case of no existence of any bead, or γ in the case that γ common beads exist in the main diagrams.For our example, the intersection of the two main diagrams is as shown in diagram 5:
in the case of no existence of any bead, or γ in the case that γ common beads exist in the main diagrams.For our example, the intersection of the two main diagrams is as shown in diagram 5:
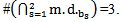 The two principle theorems about the idea of the intersection of any main diagrams are:Theorem (2.4.1.): [6] For any e ≥ 2, the following holds:1-
The two principle theorems about the idea of the intersection of any main diagrams are:Theorem (2.4.1.): [6] For any e ≥ 2, the following holds:1- 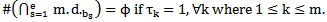 2- Let
2- Let 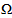 be the number of parts of
be the number of parts of 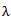 which satisfies the condition
which satisfies the condition 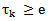 for some k, then:
for some k, then: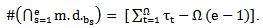 Theorem (2.4.2.): [6]1- Let
Theorem (2.4.2.): [6]1- Let 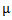 be a partition of r and
be a partition of r and 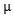 is w-regular, then:
is w-regular, then: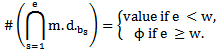 2- Let
2- Let 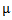 be a partition of r and
be a partition of r and 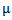 is h-restricted, then:
is h-restricted, then: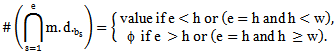 Also, S. M. Mahmood in [7] gave the same subject by using a new technique which supported the results of Mahmood in [6].
Also, S. M. Mahmood in [7] gave the same subject by using a new technique which supported the results of Mahmood in [6].
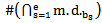 in the normal main diagrams.To realize these facts, we study the composition application for each degree apart on the previous example where
in the normal main diagrams.To realize these facts, we study the composition application for each degree apart on the previous example where 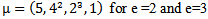 as follows:
as follows:
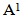 )
)

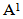 )
)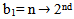 row in the case b2 and to one
row in the case b2 and to one 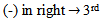 row in the case b3 and to add one (-) in right
row in the case b3 and to add one (-) in right  last row in the case be and to add one (-) in right of main diagram (A1).2. 2nd row in the case
last row in the case be and to add one (-) in right of main diagram (A1).2. 2nd row in the case 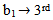 row in the case b2 and to add one (-) in right
row in the case b2 and to add one (-) in right  last row in the case be-1 and to add one
last row in the case be-1 and to add one 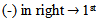 row in the case be and to add one (●) in left.
row in the case be and to add one (●) in left.  e. last row in the case
e. last row in the case 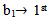 row in the case b2 and to add one (●) in left
row in the case b2 and to add one (●) in left 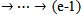 row in the case be and to add one (●) in left. This rule is clarified in diagram 9. For the above example, where
row in the case be and to add one (●) in left. This rule is clarified in diagram 9. For the above example, where 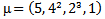 and e = 3.
and e = 3.

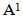 ) for e=2
) for e=2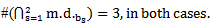


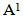 ) for e=3
) for e=3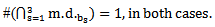
 Diagram 3. (A)
Diagram 3. (A)  Diagram 13. (A2)Again, if we use the old technique for finding any partition of any diagram (A2), the value of the partition will not be equal to the origin partition? so, we delete any effect of (-) in (A) after the position of β1, and we start with number 1 for the first (-) a (left to right) in any row exist in (A), and with number 2 for the second (-) and ..., etc, and we stop with last (-) before the position β1 in (A) as shown in diagram 7. Now, to apply "upside-down o Direct rotation of degree 1805 " on (A), the new version (A2) has the same partition of (A), see diagram 14.
Diagram 13. (A2)Again, if we use the old technique for finding any partition of any diagram (A2), the value of the partition will not be equal to the origin partition? so, we delete any effect of (-) in (A) after the position of β1, and we start with number 1 for the first (-) a (left to right) in any row exist in (A), and with number 2 for the second (-) and ..., etc, and we stop with last (-) before the position β1 in (A) as shown in diagram 7. Now, to apply "upside-down o Direct rotation of degree 1805 " on (A), the new version (A2) has the same partition of (A), see diagram 14. Diagram 7. (A)
Diagram 7. (A)  Diagram 14. (A2)Remark(3.2.1.): The main diagram (A2) in case b1 = n, plays a main role to design all the main diagrams (A2) for (b2 = n+1), ... and (be= n+(e-1)), as follows:Rule (3.2.2.): Since the main diagram (A2) in the case b1, we can find the successive main diagrams (A2) for b2, b3, ... and be , as follows:1. 1st column in the case
Diagram 14. (A2)Remark(3.2.1.): The main diagram (A2) in case b1 = n, plays a main role to design all the main diagrams (A2) for (b2 = n+1), ... and (be= n+(e-1)), as follows:Rule (3.2.2.): Since the main diagram (A2) in the case b1, we can find the successive main diagrams (A2) for b2, b3, ... and be , as follows:1. 1st column in the case 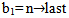 column in the case b2 and to add one (●) in up
column in the case b2 and to add one (●) in up  column in the case b3 and to add one (●) in up
column in the case b3 and to add one (●) in up  column in the case be and to add one (●) in up of main diagram (A2 ).2. 2nd column in the case
column in the case be and to add one (●) in up of main diagram (A2 ).2. 2nd column in the case  column in the case b2 and to add one (-) in
column in the case b2 and to add one (-) in  column in the case b3 and to add one (●) in up
column in the case b3 and to add one (●) in up 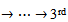 column in the case be and to add one (●) in up.
column in the case be and to add one (●) in up. e. last column in the case
e. last column in the case  column in the case b2 and to add one (-) in
column in the case b2 and to add one (-) in  column in the case be and to add one (-) in down. To check this rule For our example, where
column in the case be and to add one (-) in down. To check this rule For our example, where 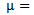
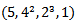 and e = 3, see diagram 15 below:
and e = 3, see diagram 15 below:

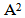 ) for e=2
) for e=2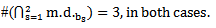

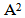 ) for e=3
) for e=3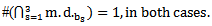

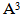 )
)
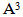 )
)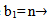 last row in the case b2 and to add one (●) in
last row in the case b2 and to add one (●) in  row in the case b3 and to add one (●) in
row in the case b3 and to add one (●) in  row in the case be and to add one (●) in right of main diagram (A3).2. 2nd row in the case
row in the case be and to add one (●) in right of main diagram (A3).2. 2nd row in the case  row in the case b2 and to add one (-) in left
row in the case b2 and to add one (-) in left  row in the cas b3 and to add one (●) in right
row in the cas b3 and to add one (●) in right  row in the case be and to add one (●) in right.
row in the case be and to add one (●) in right. e) last row in the case
e) last row in the case  row in the case b2 and to add one (-) in left
row in the case b2 and to add one (-) in left  row in the case be and to add one (-) in left. To materialize rule (3.3.2) For the our example for e = 3, see diagram 20:
row in the case be and to add one (-) in left. To materialize rule (3.3.2) For the our example for e = 3, see diagram 20: 

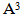 ) for e=2
) for e=2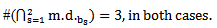

 ) for e=3
) for e=3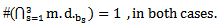
 β - Numbers = (Direct Rotation of degree 270o o Upside-Down) β - Numbersb) (Upside-Down o Direct Rotation of degree 180o)
β - Numbers = (Direct Rotation of degree 270o o Upside-Down) β - Numbersb) (Upside-Down o Direct Rotation of degree 180o) β - Numbers = (Direct Rotation of degree 180o o Upside-Down) β - Numbersc) (Upside-Down o Direct Rotation of degree 270o)
β - Numbers = (Direct Rotation of degree 180o o Upside-Down) β - Numbersc) (Upside-Down o Direct Rotation of degree 270o) β - Numbers = (Direct Rotation of degree 90o o Upside-Down) β - Numbers
β - Numbers = (Direct Rotation of degree 90o o Upside-Down) β - Numbers Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML