-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(6): 445-453
doi:10.5923/j.ajms.20130306.20
Some Embedding Theorems and Properties of Riesz Potentials
Rahim M. Rzaev1, Fuad N. Aliyev2
1Institute of Mathematics and Mechanics of National Academy of Sciences of Azerbaijan; Baku; AZ1141, Azerbaijan
2Azerbaijan State Pedagogical University; Baku; AZ1000, Azerbaijan
Correspondence to: Rahim M. Rzaev, Institute of Mathematics and Mechanics of National Academy of Sciences of Azerbaijan; Baku; AZ1141, Azerbaijan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
It is well known that potential type integrals play an important role in research of the partial differential equations. The present paper studies properties of Riesz potential in terms of local oscillation of functions.
Keywords: local oscillation, bounded mean oscillation, Morrey spaces, Riesz potential
Cite this paper: Rahim M. Rzaev, Fuad N. Aliyev, Some Embedding Theorems and Properties of Riesz Potentials, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 445-453. doi: 10.5923/j.ajms.20130306.20.
Article Outline
1. Introduction
- Let
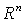 be
be 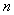 -dimensional Euclidean space of the points
-dimensional Euclidean space of the points 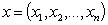 , and
, and 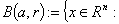
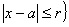 be a closed ball in
be a closed ball in 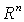 of radius
of radius 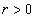 with the center at point
with the center at point 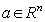 . Denote by
. Denote by 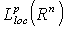 ,
, 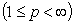 , a class of all local
, a class of all local 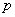 -power summable functions defined on
-power summable functions defined on 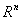 and by
and by 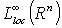 the class of all local bounded functions defined on
the class of all local bounded functions defined on 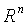 . By
. By 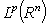 we mean the usual Lebesgue space on
we mean the usual Lebesgue space on 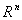 , and we denote by
, and we denote by 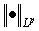 the corresponding norm, that is
the corresponding norm, that is 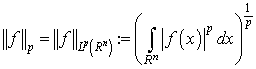 if
if 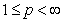 , and
, and 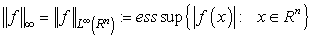 . Denote by
. Denote by 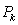 the totality of all polynomials on
the totality of all polynomials on  whose degrees are equal to or less than
whose degrees are equal to or less than  . Let
. Let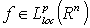 ,
, 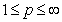 ,
, 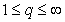 ,
, 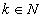 (
(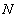 is the set of all positive integers). Define the following functions
is the set of all positive integers). Define the following functions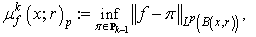
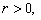
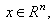
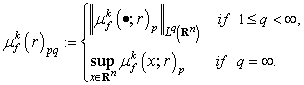 Let
Let 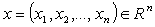 ,
, 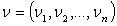 ,
, 
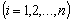 be non-negative integers,
be non-negative integers, 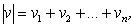
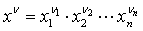 . Apply the orthogonalization process by the scalar product
. Apply the orthogonalization process by the scalar product 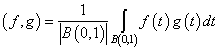 to the system of the power functions
to the system of the power functions 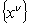 ,
, 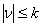 ,
, 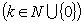 arranged by partially lexicographic order1 [1], where
arranged by partially lexicographic order1 [1], where 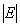 is the Lebesque measure of the set
is the Lebesque measure of the set 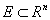 . Denote by
. Denote by 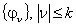 the obtained orthogonal normed system. Let
the obtained orthogonal normed system. Let 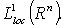 . Suppose that ([2],[3]):
. Suppose that ([2],[3]): 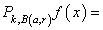
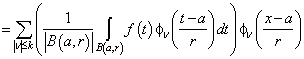 .It is obvious that
.It is obvious that 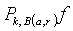 is a polynomial degree of which is equal or less than
is a polynomial degree of which is equal or less than 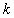 .Denote
.Denote 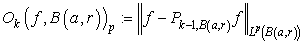 for
for 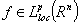
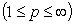 . Let us call
. Let us call 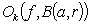 local oscillation of
local oscillation of 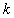 -th order of the function
-th order of the function 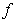 on the ball
on the ball 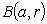 in the metric of
in the metric of 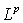 . Note that if
. Note that if  then
then 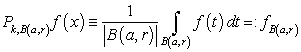 ,and therefore
,and therefore 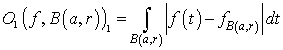 .It is known that (cf.[4]) for each polynomial
.It is known that (cf.[4]) for each polynomial 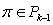 and each ball
and each ball 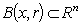 the inequality
the inequality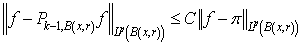 is true, where the positive constant
is true, where the positive constant 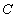 does not depend on
does not depend on 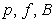 and
and 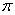 . Hence it follows that
. Hence it follows that
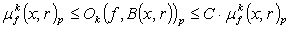 .It should be mentioned that the theory of spaces defined by local oscillation has been developed by several authors, for instance F.John and L.Nirenberg[5], S.Campanato[6], N.G.Meyers[7], S.Spanne[8], J. Peetre[9], D.Sarason[10] etc. (see also[11],[12]).Let
.It should be mentioned that the theory of spaces defined by local oscillation has been developed by several authors, for instance F.John and L.Nirenberg[5], S.Campanato[6], N.G.Meyers[7], S.Spanne[8], J. Peetre[9], D.Sarason[10] etc. (see also[11],[12]).Let 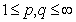 ,
, 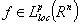 . We introduce the following denotations
. We introduce the following denotations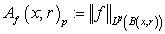 ,
, 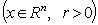 ,
, 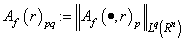 ,
, 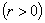 . Let
. Let 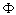 be a class of all positive monotonically increasing on
be a class of all positive monotonically increasing on 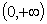 functions. Let
functions. Let 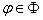 ,
, 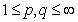 . By
. By 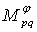 we denote the set of all the functions
we denote the set of all the functions 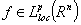 , for which
, for which 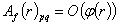 ,
, 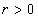 .We introduce the norm in the space
.We introduce the norm in the space 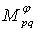 by the equality
by the equality 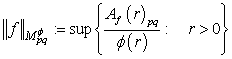 .If
.If 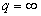 and
and 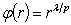 ,
, 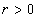 ,
, 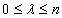 , then
, then 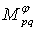
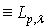 , where
, where 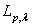 is the Morrey space, i.e.
is the Morrey space, i.e. 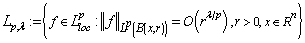 . Let
. Let 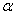 is a positive number. We denote by
is a positive number. We denote by 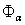 a set of all
a set of all 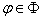 such that
such that 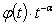 almost decreases on
almost decreases on 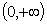 . If
. If 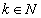 ,
, 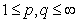 ,
, 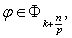 then we denote by
then we denote by 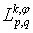 the set of all functions
the set of all functions 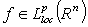 such that
such that 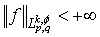 , where
, where 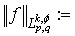
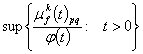 .If we consider the class
.If we consider the class 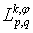 as a subset in the quotient space
as a subset in the quotient space 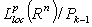 , then
, then 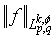 is the norm on
is the norm on 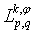 . In the introduced norm the space
. In the introduced norm the space 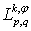 is a Banach space. If
is a Banach space. If 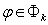 ,
, 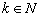 , then we will denote by
, then we will denote by 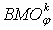 the class of all the functions
the class of all the functions 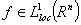 for which the following relation
for which the following relation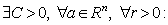
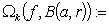
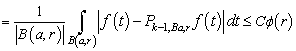 is valid.We define the norm on
is valid.We define the norm on 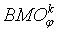 by the equality
by the equality 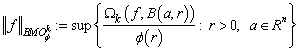 .In particular, if
.In particular, if 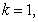
 then
then 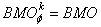 , where
, where 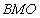 is the space of all local summable functions of bounded mean oscillation. The class
is the space of all local summable functions of bounded mean oscillation. The class 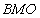 for the first time was introduced in[5].It is easy to see that if
for the first time was introduced in[5].It is easy to see that if 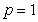 ,
, 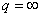 ,
, 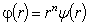 , then
, then 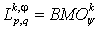 and their norms are equivalent. Consider also a class
and their norms are equivalent. Consider also a class 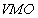 which was introduced in[10]:
which was introduced in[10]: 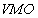 is the class of all
is the class of all 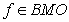 for which the relation
for which the relation 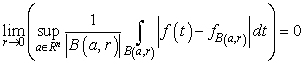 is valid. For
is valid. For 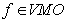 we define
we define 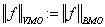 . Let
. Let 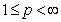 . By
. By 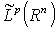 we mean the weak Lebesgue space on
we mean the weak Lebesgue space on 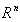 , and we denote
, and we denote 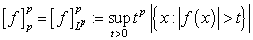 .Potential type integrals play an important role in the mathematical analysis. For the properties of Riesz potentials in terms of mean oscillations we refer the readers to[9],[4],[16] and the related papers for further information. In this paper we study the properties of Riesz potential of a function
.Potential type integrals play an important role in the mathematical analysis. For the properties of Riesz potentials in terms of mean oscillations we refer the readers to[9],[4],[16] and the related papers for further information. In this paper we study the properties of Riesz potential of a function 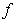 in terms of local oscillation of functions when
in terms of local oscillation of functions when 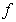 belongs to
belongs to 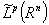 ,
, 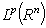 or general Morrey type spaces. The structure of the paper is as follows. In section 2 some inequalities and embedding theorems is proved. The mean results of the paper are given in Theorems 5, 6 and 7, which was proved in section 3.
or general Morrey type spaces. The structure of the paper is as follows. In section 2 some inequalities and embedding theorems is proved. The mean results of the paper are given in Theorems 5, 6 and 7, which was proved in section 3. 2. Some Inequalities and Embedding Theorems
- Proposition 1. Let
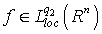 ,
, 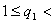
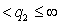 . Then the inequality
. Then the inequality 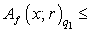
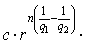
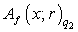
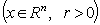 is true, where the constant
is true, where the constant 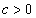 depends only on
depends only on 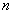 ,
, 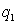 and
and 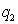 . Proof. Let
. Proof. Let 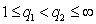 . Applying the Hölder’s Inequality we obtain
. Applying the Hölder’s Inequality we obtain 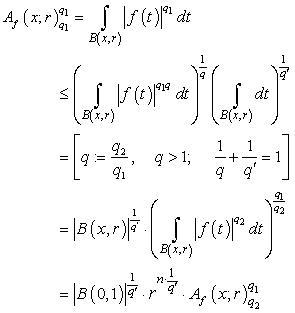 . Therefore
. Therefore 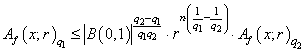 ,
, 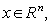
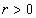 .The case
.The case 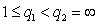 is obvious. Corollary 1. If
is obvious. Corollary 1. If 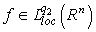 ,
, 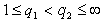 ,
, 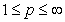 , then the inequality
, then the inequality 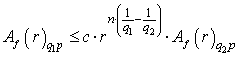 ,
, 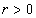 , is true. Proposition 2. Let
, is true. Proposition 2. Let 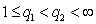 . Then there exists a function
. Then there exists a function 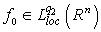 such that
such that 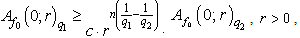 | (1) |
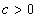 is independent of
is independent of 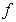 and
and 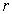 . Proof. Let
. Proof. Let 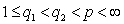 and
and 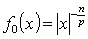 ,
, 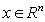 . Then we have
. Then we have 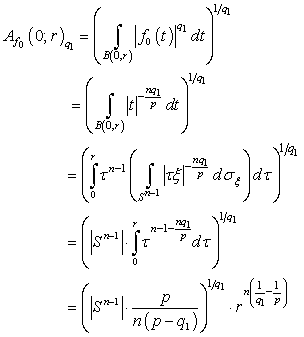 ,
,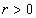 , and similarly
, and similarly 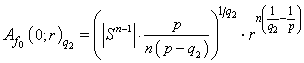 ,
, 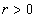 , where
, where 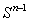 is the unit sphere,
is the unit sphere, 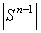 is a surface area of
is a surface area of 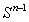 . From here we obtain the inequality (1). Proposition 3. Let
. From here we obtain the inequality (1). Proposition 3. Let 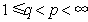 ,
, 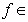
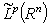 . Then
. Then 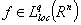 and there exists a constant
and there exists a constant 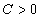 independent of
independent of 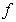 , such that
, such that 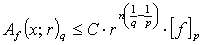 | (2) |
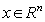 and
and 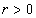 . Proof. It follows from well known equality (see[17], Chapter 1, Lemma 4.1) that (for any positive constant
. Proof. It follows from well known equality (see[17], Chapter 1, Lemma 4.1) that (for any positive constant 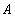 )
) 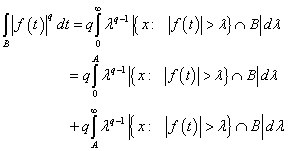
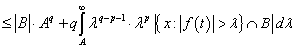
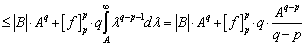 .Now choosing
.Now choosing 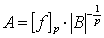 we obtain
we obtain 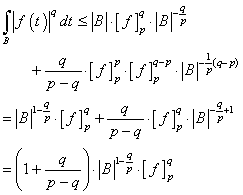 From here we obtain the inequality (1) with
From here we obtain the inequality (1) with 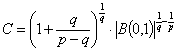 . Remark 1. In the case
. Remark 1. In the case 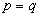 the inequality (2), in general, is not true. For instance, the function
the inequality (2), in general, is not true. For instance, the function 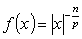 belong to
belong to 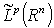 , but
, but 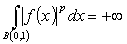 . Proposition 4. Let
. Proposition 4. Let 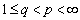 ,
, 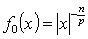 ,
, 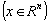 . Then
. Then 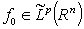 and there exists a constant
and there exists a constant 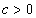 , depends only on
, depends only on 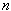 ,
, 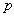 ,
, 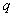 , such that
, such that 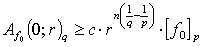 | (3) |
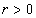 . Proof. We have
. Proof. We have 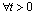
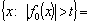
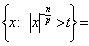
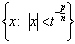 .Therefore
.Therefore 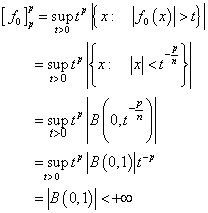 .This means that
.This means that 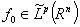 and
and 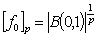 . Further we obtain
. Further we obtain 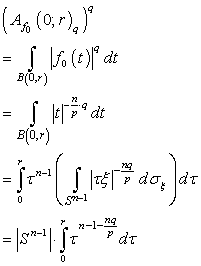
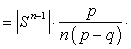
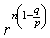 ,
, 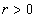 , where
, where 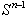 is the unit sphere,
is the unit sphere, 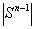 is a surface area of
is a surface area of 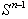 . From here
. From here 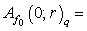
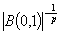
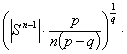
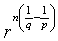
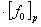 ,
, 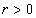 . The previous proposition shows that it is impossible to improve the estimation (2). Proposition 5. Let
. The previous proposition shows that it is impossible to improve the estimation (2). Proposition 5. Let 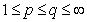 ,
, 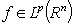 . Then the inequality
. Then the inequality 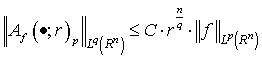 | (4) |
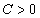 is independent of
is independent of 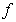 ,
, 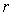 . Proof. At first we consider the case
. Proof. At first we consider the case 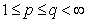 . Then we have
. Then we have 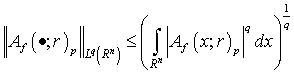
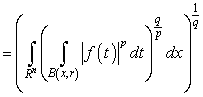
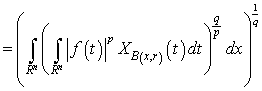
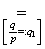
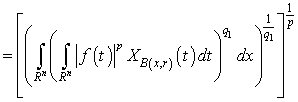 ,where
,where 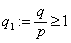 . Further, applying the Minkowski’s Inequality we have
. Further, applying the Minkowski’s Inequality we have 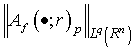
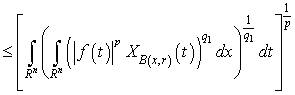
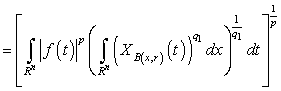
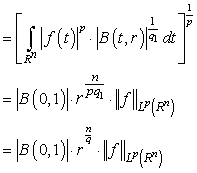 ,where
,where 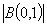 is the volume of the unit ball
is the volume of the unit ball 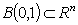 . In the case
. In the case 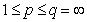 the proof of inequality (4) is obvious. The following proposition shows that it is impossible to improve the estimation (4) in the case
the proof of inequality (4) is obvious. The following proposition shows that it is impossible to improve the estimation (4) in the case 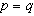 . Proposition 6. Let
. Proposition 6. Let 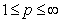 . Then there exists the function
. Then there exists the function 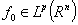 such that for
such that for 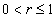 the inequality
the inequality 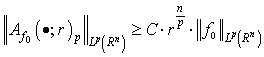 | (5) |
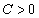 is independent of
is independent of 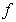 and
and 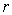 . Proof. Let
. Proof. Let 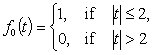 .If
.If 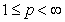 ,
, 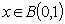 ,
, 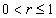 , then we obtain
, then we obtain 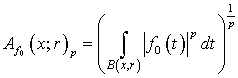
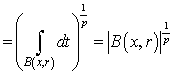 .If
.If 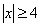 ,
, 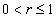 , then
, then 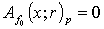 . Besides, for all
. Besides, for all 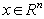 ,
, 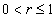
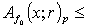
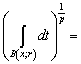
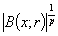 .Thus the function
.Thus the function 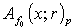 is integrable on the
is integrable on the 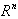 with respect to argument
with respect to argument 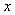 . Further we obtain that if
. Further we obtain that if 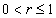 , then
, then 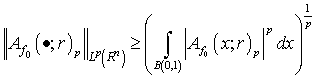
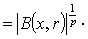
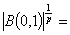
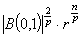 .It is obvious that
.It is obvious that 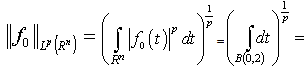
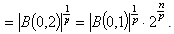 Therefore we obtain that
Therefore we obtain that 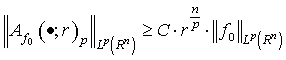 ,
, 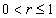 .In the case
.In the case 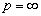 the arguments are similar. With help of Proposition 3, Proposition 5 and Corollary 1 we obtain correspondingly, the following theorems. Theorem 1. Let
the arguments are similar. With help of Proposition 3, Proposition 5 and Corollary 1 we obtain correspondingly, the following theorems. Theorem 1. Let 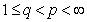 . Then
. Then 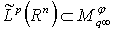 and
and 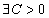
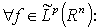
 , where
, where 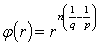 ,
, 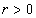 . Theorem 2. Let
. Theorem 2. Let 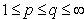 ,
, 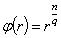
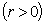 . Then
. Then 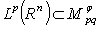 and
and 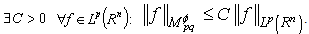 Theorem 3. Let
Theorem 3. Let 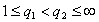 ,
, 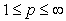 and
and 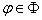 . Then
. Then 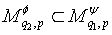 and
and 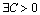
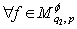 :
: 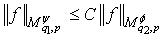 , where
, where 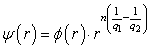 ,
, 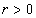 .
. 3. Properties of Riesz Potentials
- Consider the following potential type integral operator
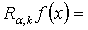
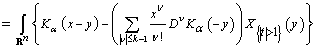
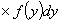 where
where 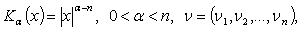
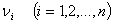 are non-negative integers,
are non-negative integers, 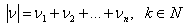 ,
, 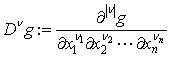 ,
,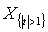 is the characteristic function of the set
is the characteristic function of the set 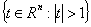 . Operator
. Operator 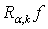 is a certain modification of the Riesz potential
is a certain modification of the Riesz potential 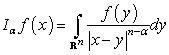 .It should be noted that if
.It should be noted that if 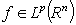 and
and 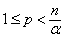 , then the integral
, then the integral 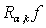 differs from integral
differs from integral 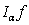 by a polynomial power of which is equal or less than
by a polynomial power of which is equal or less than 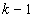 . If
. If 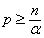 , then the potential
, then the potential 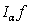 is defined not for all functions
is defined not for all functions 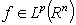 . Moreover, if
. Moreover, if 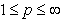 and
and 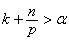 , for example, then for
, for example, then for 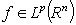 integral
integral 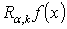 absolutely converges almost everywhere. Note that modified Riesz potential similar to the
absolutely converges almost everywhere. Note that modified Riesz potential similar to the 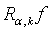 was considered, for example, in T.Kurokawa[13], T.Shimomura and Y. Mizuta[14] etc. (see also[15]).The following assertion holds true. Theorem 4[16]. Let
was considered, for example, in T.Kurokawa[13], T.Shimomura and Y. Mizuta[14] etc. (see also[15]).The following assertion holds true. Theorem 4[16]. Let 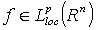 ,
, 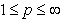 ,
, 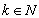 ,
, 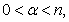
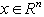 and
and 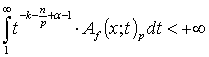 .Then the inequality
.Then the inequality 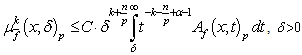 | (6) |
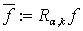 , and constant
, and constant 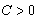 does not depend on
does not depend on 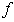 ,
, 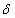 and
and 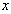 . Corollary 2. Let
. Corollary 2. Let 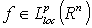 ,
, 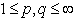 ,
, 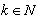 ,
, 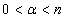 and
and 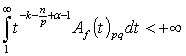 .Then inequality
.Then inequality 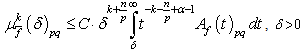 | (7) |
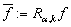 , and constant
, and constant 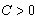 does not depend on
does not depend on 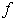 and
and 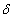 . Theorem 5. Let
. Theorem 5. Let 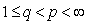 ,
, 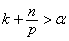 . If
. If 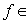
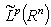 , then
, then 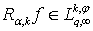 and
and 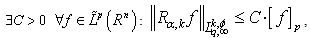 where
where 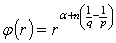 ,
, 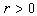 . Proof. With help of Proposition 3 and Theorem 4 we have
. Proof. With help of Proposition 3 and Theorem 4 we have 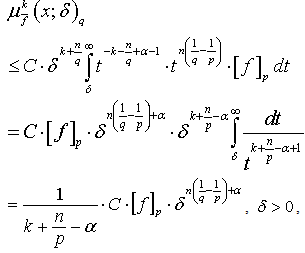 where
where 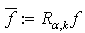 . From here the theorem statement easily turns out. Corollary 3. Let
. From here the theorem statement easily turns out. Corollary 3. Let 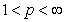 ,
, 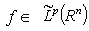 ,
, 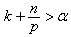 ,
, 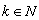 ,
, 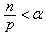 . Then
. Then 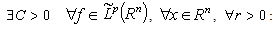
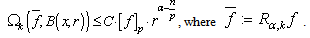 Corollary 4. Let
Corollary 4. Let 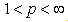 ,
, 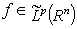 ,
, 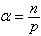 . Then
. Then 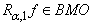 and
and 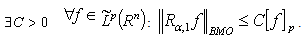 Corollary 5. If
Corollary 5. If 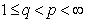 ,
, 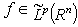 ,
, 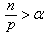 , then
, then 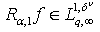 , where
, where 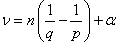 , and
, and 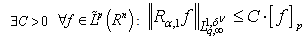 . Theorem 6. Let
. Theorem 6. Let 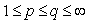 ,
, 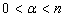 ,
, 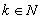 ,
, 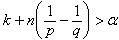 ,
, 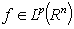 . Then
. Then 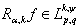 and
and 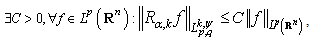 where
where 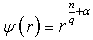 ,
, 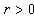 . In the case
. In the case 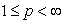 ,
, 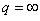 in addition
in addition 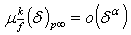 ,
, 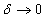 , where
, where 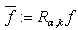 . Proof. Taking into account the inequalities (4) and (7), it is easy to obtain the inequality
. Proof. Taking into account the inequalities (4) and (7), it is easy to obtain the inequality 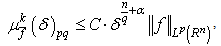 | (8) |
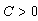 is independent of
is independent of 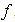 ,
, 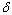 . From here we obtain that
. From here we obtain that 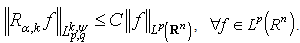 If
If 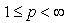 ,
, 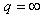 , then
, then 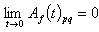 . Therefore if
. Therefore if 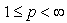 ,
, 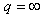 and
and 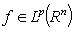 , then from estimation (7), in addition, we have
, then from estimation (7), in addition, we have 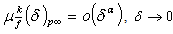 . Corollary 6. Let
. Corollary 6. Let 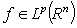 ,
, 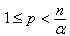 ,
, 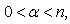
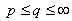 ,
, 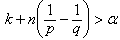 . Then
. Then 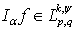 and
and 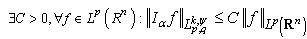 , where
, where 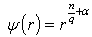 ,
, 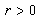 . In the case
. In the case 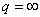 , in addition, we have
, in addition, we have 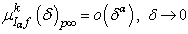 .Corollary 7. Let
.Corollary 7. Let 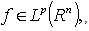
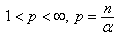 . Then
. Then 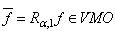 and
and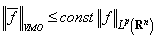 . Corollary 8. Let
. Corollary 8. Let 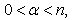
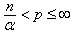 ,
, 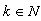 ,
, 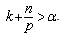 If
If 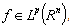 , then
, then 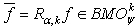 and
and 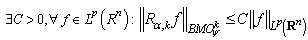 , where
, where 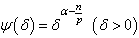 . If
. If 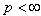 , then in addition,
, then in addition, 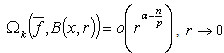 . Theorem 7. Let
. Theorem 7. Let 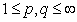 ,
, 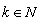 ,
, 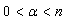 ,
, 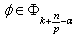 and
and 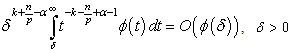 .If
.If 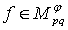 , then
, then 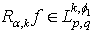 and
and 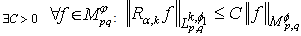 , where
, where 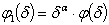 ,
, 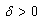 . Let
. Let 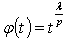 ,
, 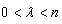 . Then
. Then 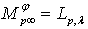 and
and 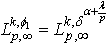 . From Theorem 7 we obtain that if
. From Theorem 7 we obtain that if 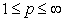 ,
, 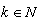 ,
, 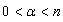 ,
, 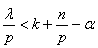 , then
, then 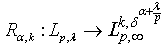 , i.e. the operator
, i.e. the operator 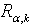 boundedly acts from
boundedly acts from 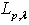 into
into 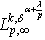 . Corollary 9. If
. Corollary 9. If 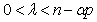 , then
, then 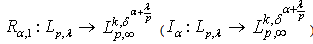 . Corollary 10. If
. Corollary 10. If 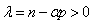 , then
, then 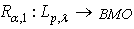 . Corollary 11. If
. Corollary 11. If 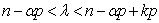 ,
, 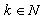 ,
, 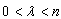 , then
, then 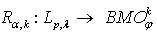 , where
, where 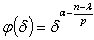 .
. Notes
- 1. It means that
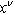 precedes
precedes 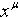 if either
if either 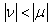 , or
, or 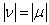 but the first nonzero difference
but the first nonzero difference 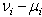 is negative.
is negative. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML -th order mean oscillation. Dokl. Akad. Nauk (Russia), 1997, v.356, No5, pp.602-604. (Russian)
-th order mean oscillation. Dokl. Akad. Nauk (Russia), 1997, v.356, No5, pp.602-604. (Russian) spaces. J. Functional Analysis, 1969, v.4, p.71-87.
spaces. J. Functional Analysis, 1969, v.4, p.71-87. . Analysis Mathematica, 1999, v.25, pp.205-210.
. Analysis Mathematica, 1999, v.25, pp.205-210. . Embedding theorems. Harmonic analysis. Proc. Inst. Math. and Mech. of NAS of Azerb., Baku, 2007, Issue 13, pp.281-294.
. Embedding theorems. Harmonic analysis. Proc. Inst. Math. and Mech. of NAS of Azerb., Baku, 2007, Issue 13, pp.281-294.