Reetu, S. C. Malik
Department of Statistics, M.D. University, Rohtak, 124001, India
Correspondence to: S. C. Malik, Department of Statistics, M.D. University, Rohtak, 124001, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The main intension of this paper is to determine reliability measures of a parallel system of two identical units under the aspect of priority to preventive maintenance over repair and replacement of the unit. The unit has two modes-operative and complete failure. The operation of at least one unit is sufficient for smooth functioning of the system. A single repair facility is provided immediately to conduct repair activities. The unit undergoes for preventive maintenance after fixed maximum operation time. However, the unit is replaced by new one if its repair is not possible by server in the given maximum repair time ‘t’. Priority is given to preventive maintenance of one unit over repair and replacement of the other unit. The unit works as new after preventive maintenance and repair. The random variables associated with failure, preventive maintenance, repair and replacement times of the unit are statistically independent. The distributions of failure time and the times to which unit undergoes to preventive maintenance and replacement are taken as negative exponential. But, the distributions of preventive maintenance, repair and replacement times are assumed as arbitrary. The semi-Markov process and regenerative point technique are used to derive expressions for system performance measures in steady state. A particular case is considered to depict the graphical behavior of mean time to system failure (MTSF), availability and profit function. The cost benefit analysis of the system model is done under different repair cost policies.
Keywords:
Parallel System, Preventive Maintenance, Maximum Operation Time, Maximum Repair, Priority, Reliability Measures
Cite this paper: Reetu, S. C. Malik, A Parallel System with Priority to Preventive Maintenance Subject to Maximum Operation and Repair Times, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 436-444. doi: 10.5923/j.ajms.20130306.19.
1. Introduction
The requirements of parallel operation of the components in repairable systems have been increasing day by day to maintain reliability and sharing of working stress. Therefore, reliability models of parallel systems have been proposed by the researchers including Kishan and Kumar[1] and Kumar et al.[2] under the assumptions that faults are rectifiable and systems can work for a long time without requiring any maintenance. But continued operations and ageing of operable systems reduce their performance, reliability and safety. Thus, to slow the deterioration process as well as to restore the system in a younger age or state, the preventive maintenance can be conducted after maximum operation time. Malik and Nandal[3] discussed a cold standby system introducing the concept of preventive maintenance after a maximum operation time. Also, sometimes it becomes necessary to make replacement of a failed component (or a unit) by new one when its repair is not possible by the server in a pre-specific time in order to avoid unnecessary expanses on repair. Kumar et al.[4] analyzed a computer system with maximum operation and repair times. Furthermore, the concept of priority in repair disciplines proved as the one to reduce down time of the system and to minimize the operating cost. Malik and Sureria[5] investigated probabilistically a computer system with priority to hardware repair over software replacement.Incorporating the ideas of preventive maintenance, replacement of the unit and priority in repair disciplines, here a parallel system of two identical units is analyzed stochastically in detail adopting semi-Markov process and regenerative point technique. The unit has direct complete failure from normal mode. The operation of at least one unit is sufficient for smooth functioning of the system. There is a single server who visits the system immediately to conduct repair activities. The unit undergoes for preventive maintenance after a fixed maximum operation time. However, the unit is replaced by new one if its repair is not possible by server in the given maximum repair time‘t’. Priority is given to preventive maintenance of one unit over repair and replacement of the other unit. The unit works as new after preventive maintenance and repair. All random variables are statistically independent. The distributions of failure time and the times to which unit undergoes to preventive maintenance and replacement are taken as negative exponential whereas preventive maintenance, repair and replacement times are arbitrarily distributed with different probability density functions. The expressions for system performance measures in steady state are derived. A particular case is considered to depict the graphical behavior of mean time to system failure (MTSF), availability and profit function. The cost benefit analysis of the system model is done under different repair cost policies.
2. Notations
E: Set of regenerative states 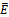 : Set of non-regenerative statesλ: Constant failure rateα0: The rate by which system undergoes for preventive maintenance (called maximum constant rate of operation time)β0: The rate by which system undergoes for replacement (called maximum constant rate of repair time)FUr /FWr: The unit is failed and under repair/waiting for repairFURp: The unit is failed and under replacementUPm: The unit is under preventive maintenanceWPm: The unit is waiting for preventive maintenanceFUR/FWR: The unit is failed and under repair / waiting for repair continuously from previous stateFURP: The unit is failed and under replacement continuously from previous stateUPM: The unit is under preventive maintenance continuously from previous stateWPM: The unit is waiting for preventive maintenance continuously from previous stateg(t)/G(t): pdf/cdf of repair time of the unit f(t)/F(t): pdf/cdf of preventive maintenance time of the unitr(t)/R(t): pdf/cdf of replacement time of the unitqij (t)/ Qij(t): pdf / cdf of passage time from regenerative state Si to a regenerative state Sj or to a failed state Sj without visiting any other regenerative state in (0, t]qij.kr (t)/Qij.kr(t): pdf/cdf of direct transition time from regenerative state Si to a regenerative state Sj or to a failed state Sj visiting state Sk,Sr once in (0, t]Mi(t) : Probability that the system up initially in state Si ∈ E is up at time t without visiting to any regenerative stateWi(t) :Probability that the server is busy in the state Si up to time ‘t’ without making any transition to any other regenerative state or returning to the same state via one or more non-regenerative states.mij: Contribution to mean sojourn time (μi) in state Si when system transits directly to state Sj so that
: Set of non-regenerative statesλ: Constant failure rateα0: The rate by which system undergoes for preventive maintenance (called maximum constant rate of operation time)β0: The rate by which system undergoes for replacement (called maximum constant rate of repair time)FUr /FWr: The unit is failed and under repair/waiting for repairFURp: The unit is failed and under replacementUPm: The unit is under preventive maintenanceWPm: The unit is waiting for preventive maintenanceFUR/FWR: The unit is failed and under repair / waiting for repair continuously from previous stateFURP: The unit is failed and under replacement continuously from previous stateUPM: The unit is under preventive maintenance continuously from previous stateWPM: The unit is waiting for preventive maintenance continuously from previous stateg(t)/G(t): pdf/cdf of repair time of the unit f(t)/F(t): pdf/cdf of preventive maintenance time of the unitr(t)/R(t): pdf/cdf of replacement time of the unitqij (t)/ Qij(t): pdf / cdf of passage time from regenerative state Si to a regenerative state Sj or to a failed state Sj without visiting any other regenerative state in (0, t]qij.kr (t)/Qij.kr(t): pdf/cdf of direct transition time from regenerative state Si to a regenerative state Sj or to a failed state Sj visiting state Sk,Sr once in (0, t]Mi(t) : Probability that the system up initially in state Si ∈ E is up at time t without visiting to any regenerative stateWi(t) :Probability that the server is busy in the state Si up to time ‘t’ without making any transition to any other regenerative state or returning to the same state via one or more non-regenerative states.mij: Contribution to mean sojourn time (μi) in state Si when system transits directly to state Sj so that 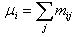 and mij =
and mij = 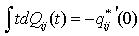
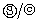 : Symbol for Laplace-Stieltjes convolution/Laplace convolution*/**: Symbol for Laplace Transformation /Laplace Stieltjes Transformation
: Symbol for Laplace-Stieltjes convolution/Laplace convolution*/**: Symbol for Laplace Transformation /Laplace Stieltjes Transformation
3. Transition Probabilities and Mean Sojourn Times
Simple probabilistic considerations yield the following expressions for the non-zero elements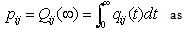 | (1) |
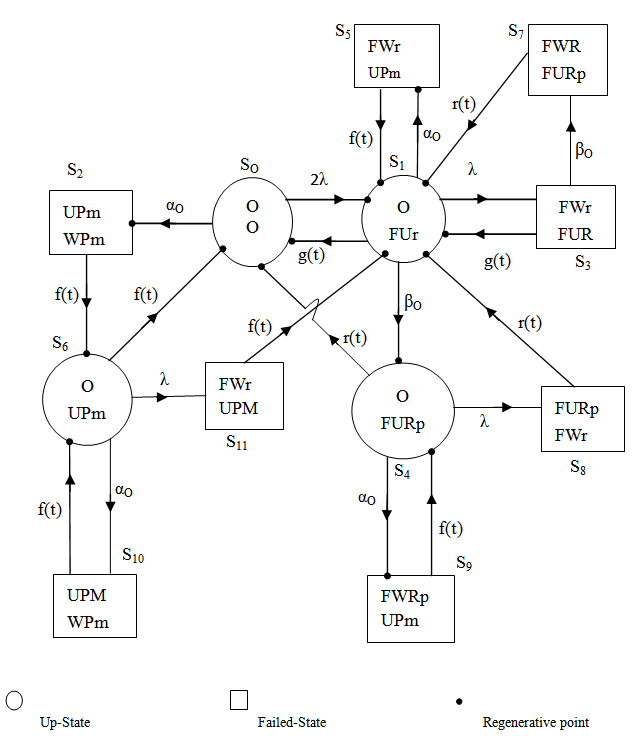 | Figure 1. State Transition Diagram |
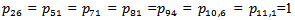 | (2) |
It can be easily verify that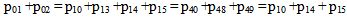
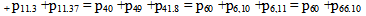
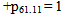 The mean sojourn times
The mean sojourn times 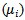 is in the state Si are
is in the state Si are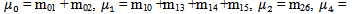
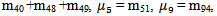
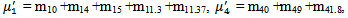
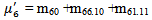
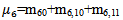 | (3) |
4. Reliability and Mean Time to System Failure (MTSF)
Let 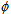 i(t) be the cdf of first passage time from regenerative state Si to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for
i(t) be the cdf of first passage time from regenerative state Si to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for 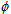 i(t):
i(t):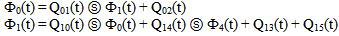
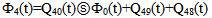 | (4) |
Taking LST of above relations (4) and solving for 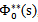 , we have
, we have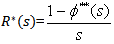 | (5) |
The reliability of the system model can be obtained by taking Inverse Laplace transform of (5). The mean time to system failure (MTSF) is given by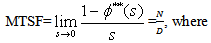 | (6) |
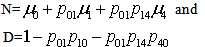 | (7) |
5. Steady State Availability
Let Ai(t) be the probability that the system is in up-state at instant ‘t’ given that the system entered regenerative state Si at t = 0. The recursive relations for 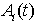 are given as:
are given as: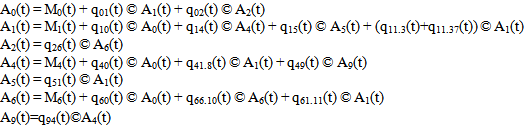 | (8) |
Where 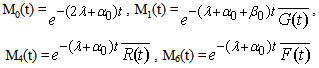 | (9) |
Taking LT of above relations (8) and solving for A0*(s).The steady state availability is given by 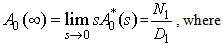 | (10) |
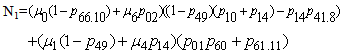 | (11) |
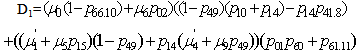 | (12) |
6. Busy Period Analysis for Server
(a) Due to Repair Let 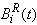 be the probability that the server is busy in repair the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for
be the probability that the server is busy in repair the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for 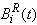 are as follows:
are as follows: 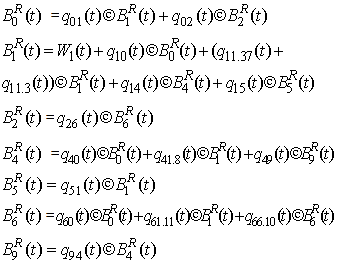 | (13) |
where, 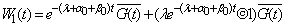 | (14) |
Taking LT of above relations (13) and solving for 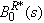 . The time for which server is busy due to repair is given by
. The time for which server is busy due to repair is given by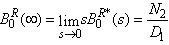 | (15) |
where 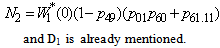 | (16) |
(b) Due to ReplacementLet 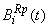 be the probability that the server is busy in replacement the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for
be the probability that the server is busy in replacement the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for 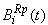 are as follows:
are as follows: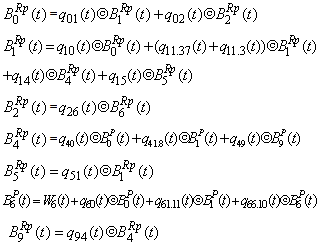 | (17) |
where, 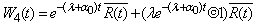 | (18) |
Taking LT of above relations (17) and solving for 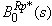 . The time for which server is busy due to replacement is given by
. The time for which server is busy due to replacement is given by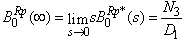 | (19) |
Where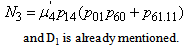 | (20) |
(c) Due to Preventive MaintenanceLet 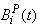 be the probability that the server is busy in preventive maintenance the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0.The recursive relations for
be the probability that the server is busy in preventive maintenance the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0.The recursive relations for 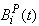 are as follows:
are as follows: 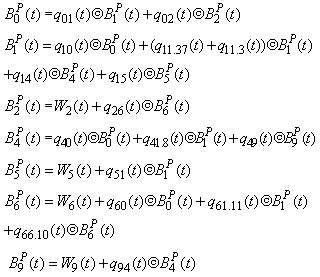 | (21) |
Where 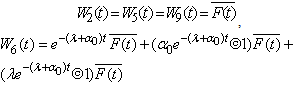 | (22) |
Taking LT of above relations (21) and solving for 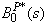 . The time for which server is busy due to preventive maintenance is given by
. The time for which server is busy due to preventive maintenance is given by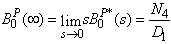 | (23) |
Where,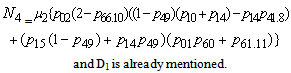 | (24) |
7. Expected Number of Repairs
Let 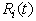 be the expected number of repairs by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for
be the expected number of repairs by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for 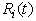 are given as:
are given as: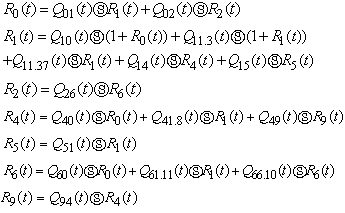 | (25) |
Taking LST of above relations (25) and solving for 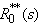 . The expected no. of repairs per unit time by the server are giving by
. The expected no. of repairs per unit time by the server are giving by 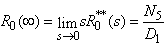 | (26) |
where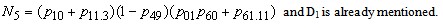 | (27) |
8. Expected Number of Replacements
Let 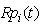 be the expected number of replacements by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for
be the expected number of replacements by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for 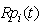 are given as:
are given as: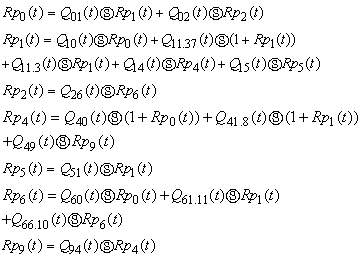 | (28) |
Taking LST of above relations (28) and solving for 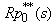 . The expected number of replacements per unit time are given by
. The expected number of replacements per unit time are given by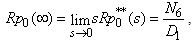 | (29) |
where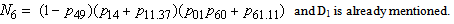 | (30) |
9. Expected Number of Preventive Maintenances
Let 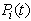 be the expected number of preventive maintenance by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for
be the expected number of preventive maintenance by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for 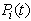 are given as:
are given as: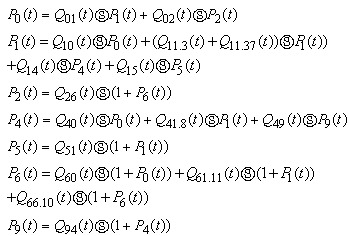 | (31) |
Taking LST of above relations (31) and solving for 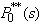 . The expected number of preventive maintenances per unit time are given by
. The expected number of preventive maintenances per unit time are given by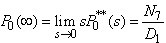 | (32) |
where 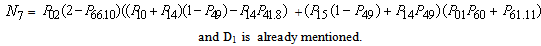 | (33) |
10. Cost-Benefit Analysis
The profit incurred to the system model in steady state can be obtained as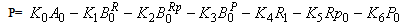 WhereK0 = Revenue per unit up-time of the system K1 = Cost per unit time for which server is busy due to repair K2 = Cost per unit time for which server is busy due to replacementK3 = Cost per unit time for which server is busy due to preventive maintenanceK4 = Cost per unit time repair K5 = Cost per unit time replacement K6 = Cost per unit time preventive maintenance
WhereK0 = Revenue per unit up-time of the system K1 = Cost per unit time for which server is busy due to repair K2 = Cost per unit time for which server is busy due to replacementK3 = Cost per unit time for which server is busy due to preventive maintenanceK4 = Cost per unit time repair K5 = Cost per unit time replacement K6 = Cost per unit time preventive maintenance
11. Particular Case
Suppose 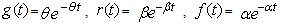 We can obtain the following results:
We can obtain the following results: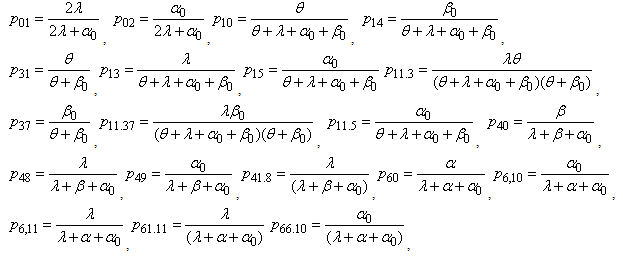 Also
Also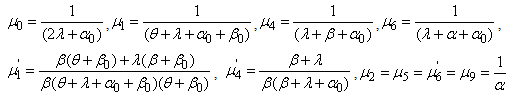 And
And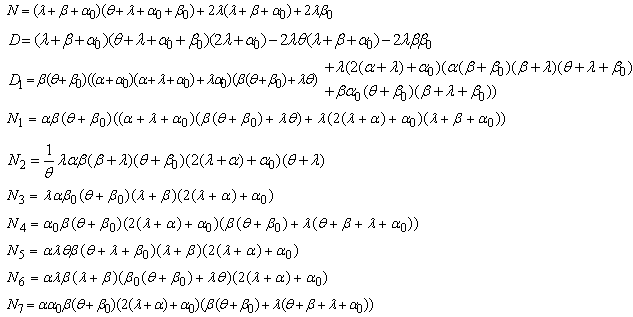
12. Conclusions
The theoretical results related to mean time to system failure (MTSF), availability and profit function are authenticated through graphs drawn for arbitrary values of various parameters and costs as shown respectively in figures 2, 3 and 4. It is found that MTSF decreases with the increase of failure rate (λ) and the rate (α0) by which unit under goes for preventive maintenance while MTSF keeps on increasing with the increase of repair rate (θ), the rate (β0) by which unit under goes for replacement and replacement rate (β). However, there is no effect of preventive maintenance rate (α) on MTSF. Figures 3 and 4 indicate that availability and profit of the system model go on decreasing with the increase of rates λ, β0 and α0. On the other hand, their values go on increasing with the increase of rates θ, β and α. Thus, the study reveals that a parallel system of two identical units in which priority is given to preventive maintenance of one unit over repair and replacement of the other unit can be made more profitable by increasing preventive maintenance and repair rates of the unit instead of its replacement by new one.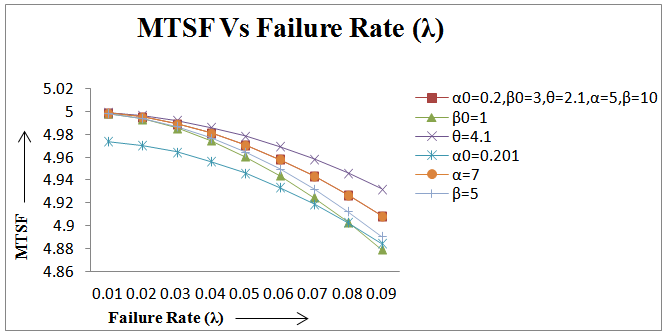 | Figure 2. MTSF Vs Failure Rate (λ) |
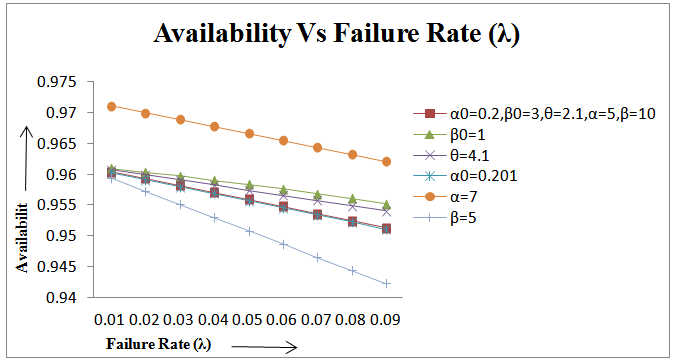 | Figure 3. Availability Vs Failure Rate (λ) |
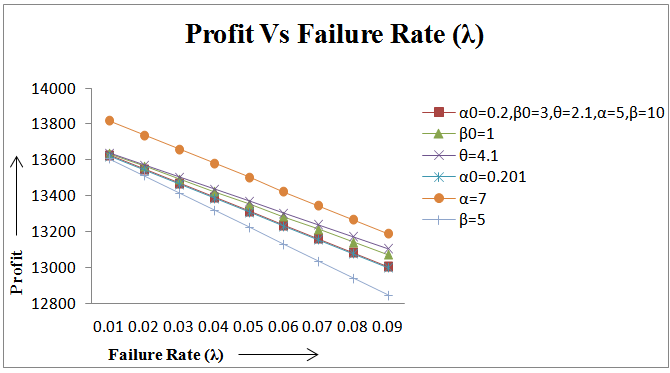 | Figure 4. Profit Vs Failure Rate (λ) |
ACKNOWLEDGEMENTS
The author Ms. Reetu is grateful to the Department of Science and Technology (DST), Govt. of India for providing financial helps under INSPIRE scheme. The authors are also grateful to the reviewer(s) for suggesting good points to make the study more important and useful.
References
| [1] | Kishan, R. and Kumar, M. (2009): Stochastic Analysis of a Two-Unit Parallel System with Preventive Maintenance. Journal of Reliability and Statistical Studies, Vol. 22, pp. 31-38. |
| [2] | Kumar, Jitender, Kadyan, M.S. and Malik, S.C. (2010): Cost-benefit analysis of a two-unit parallel system subject to degradation after repair. Journal of Applied Mathematical Sciences, Vol.4 (56), pp.2749-2758. |
| [3] | Malik, S.C. and Nandal, P. (2010): Cost-analysis of stochastic models with priority to repair over preventive maintenance subject to maximum operation time. Learning Manual on Modeling, Optimization and Their Applications, Edited Book, Excel India Publishers, pp 165-178. |
| [4] | Kumar, A., Malik, S,C. and Barak, M.S. (2012): Reliability Modeling of a Computer System with Independent H/W and S/W Failures Subject to Maximum Operation and Repair Times. International Journal of Mathematical Archive, Vol.3 (7), pp. 2622-2630. |
| [5] | Malik, S.C. and Sureria, J.K. (2012): Probabilistic Analysis of a Computer System With Priority to H/w Repair over S/w Replacement. International Journal of Statistics and Analysis, Vol.2 (4),pp.379- 389. |
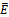 : Set of non-regenerative statesλ: Constant failure rateα0: The rate by which system undergoes for preventive maintenance (called maximum constant rate of operation time)β0: The rate by which system undergoes for replacement (called maximum constant rate of repair time)FUr /FWr: The unit is failed and under repair/waiting for repairFURp: The unit is failed and under replacementUPm: The unit is under preventive maintenanceWPm: The unit is waiting for preventive maintenanceFUR/FWR: The unit is failed and under repair / waiting for repair continuously from previous stateFURP: The unit is failed and under replacement continuously from previous stateUPM: The unit is under preventive maintenance continuously from previous stateWPM: The unit is waiting for preventive maintenance continuously from previous stateg(t)/G(t): pdf/cdf of repair time of the unit f(t)/F(t): pdf/cdf of preventive maintenance time of the unitr(t)/R(t): pdf/cdf of replacement time of the unitqij (t)/ Qij(t): pdf / cdf of passage time from regenerative state Si to a regenerative state Sj or to a failed state Sj without visiting any other regenerative state in (0, t]qij.kr (t)/Qij.kr(t): pdf/cdf of direct transition time from regenerative state Si to a regenerative state Sj or to a failed state Sj visiting state Sk,Sr once in (0, t]Mi(t) : Probability that the system up initially in state Si ∈ E is up at time t without visiting to any regenerative stateWi(t) :Probability that the server is busy in the state Si up to time ‘t’ without making any transition to any other regenerative state or returning to the same state via one or more non-regenerative states.mij: Contribution to mean sojourn time (μi) in state Si when system transits directly to state Sj so that
: Set of non-regenerative statesλ: Constant failure rateα0: The rate by which system undergoes for preventive maintenance (called maximum constant rate of operation time)β0: The rate by which system undergoes for replacement (called maximum constant rate of repair time)FUr /FWr: The unit is failed and under repair/waiting for repairFURp: The unit is failed and under replacementUPm: The unit is under preventive maintenanceWPm: The unit is waiting for preventive maintenanceFUR/FWR: The unit is failed and under repair / waiting for repair continuously from previous stateFURP: The unit is failed and under replacement continuously from previous stateUPM: The unit is under preventive maintenance continuously from previous stateWPM: The unit is waiting for preventive maintenance continuously from previous stateg(t)/G(t): pdf/cdf of repair time of the unit f(t)/F(t): pdf/cdf of preventive maintenance time of the unitr(t)/R(t): pdf/cdf of replacement time of the unitqij (t)/ Qij(t): pdf / cdf of passage time from regenerative state Si to a regenerative state Sj or to a failed state Sj without visiting any other regenerative state in (0, t]qij.kr (t)/Qij.kr(t): pdf/cdf of direct transition time from regenerative state Si to a regenerative state Sj or to a failed state Sj visiting state Sk,Sr once in (0, t]Mi(t) : Probability that the system up initially in state Si ∈ E is up at time t without visiting to any regenerative stateWi(t) :Probability that the server is busy in the state Si up to time ‘t’ without making any transition to any other regenerative state or returning to the same state via one or more non-regenerative states.mij: Contribution to mean sojourn time (μi) in state Si when system transits directly to state Sj so that 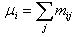 and mij =
and mij = 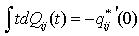
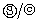 : Symbol for Laplace-Stieltjes convolution/Laplace convolution*/**: Symbol for Laplace Transformation /Laplace Stieltjes Transformation
: Symbol for Laplace-Stieltjes convolution/Laplace convolution*/**: Symbol for Laplace Transformation /Laplace Stieltjes Transformation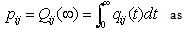
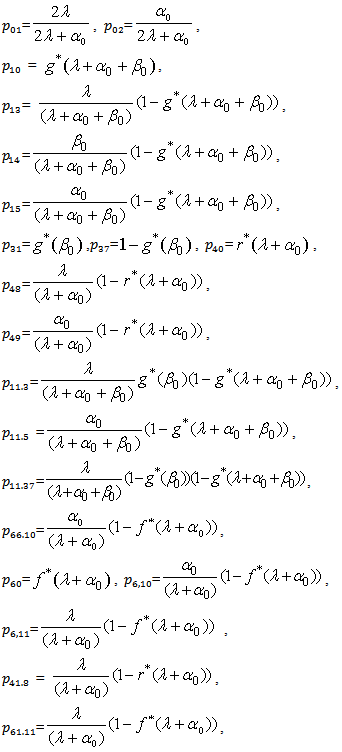

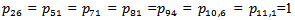
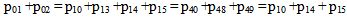
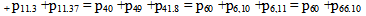
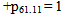 The mean sojourn times
The mean sojourn times 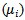 is in the state Si are
is in the state Si are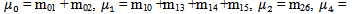
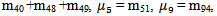
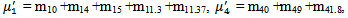
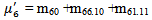
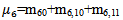
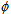 i(t) be the cdf of first passage time from regenerative state Si to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for
i(t) be the cdf of first passage time from regenerative state Si to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for 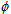 i(t):
i(t):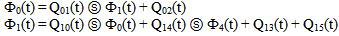
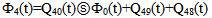
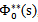 , we have
, we have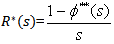
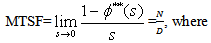
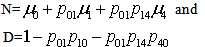
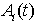 are given as:
are given as: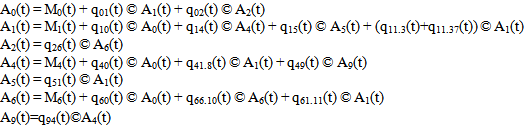
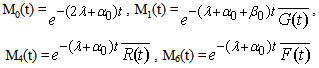
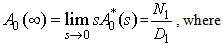
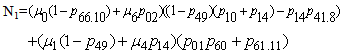
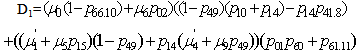
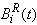 be the probability that the server is busy in repair the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for
be the probability that the server is busy in repair the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for 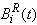 are as follows:
are as follows: 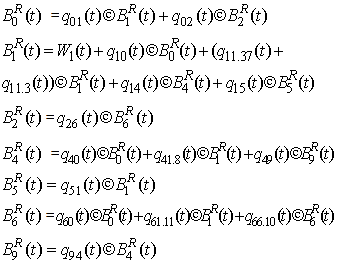
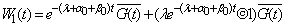
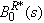 . The time for which server is busy due to repair is given by
. The time for which server is busy due to repair is given by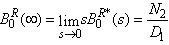
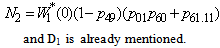
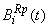 be the probability that the server is busy in replacement the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for
be the probability that the server is busy in replacement the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0. The recursive relations for 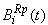 are as follows:
are as follows: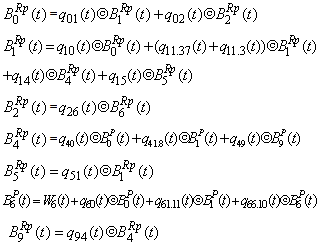
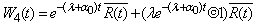
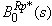 . The time for which server is busy due to replacement is given by
. The time for which server is busy due to replacement is given by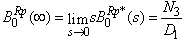
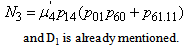
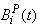 be the probability that the server is busy in preventive maintenance the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0.The recursive relations for
be the probability that the server is busy in preventive maintenance the unit at an instant ‘t’ given that the system entered regenerative state Si at t=0.The recursive relations for 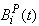 are as follows:
are as follows: 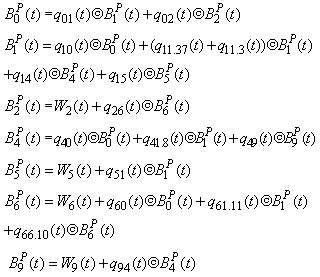
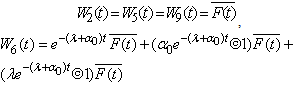
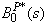 . The time for which server is busy due to preventive maintenance is given by
. The time for which server is busy due to preventive maintenance is given by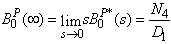
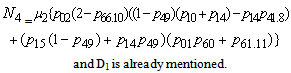
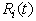 be the expected number of repairs by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for
be the expected number of repairs by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for 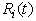 are given as:
are given as: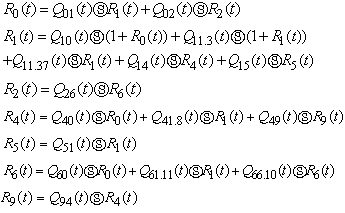
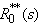 . The expected no. of repairs per unit time by the server are giving by
. The expected no. of repairs per unit time by the server are giving by 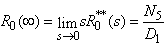
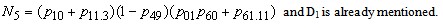
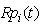 be the expected number of replacements by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for
be the expected number of replacements by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for 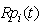 are given as:
are given as: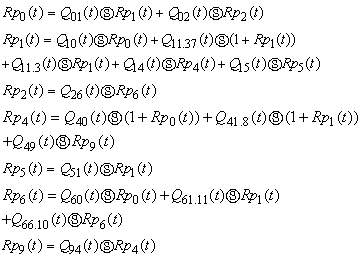
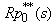 . The expected number of replacements per unit time are given by
. The expected number of replacements per unit time are given by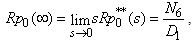
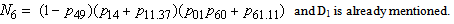
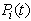 be the expected number of preventive maintenance by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for
be the expected number of preventive maintenance by the server in (0, t] given that the system entered the regenerative state Si at t = 0. The recursive relations for 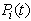 are given as:
are given as: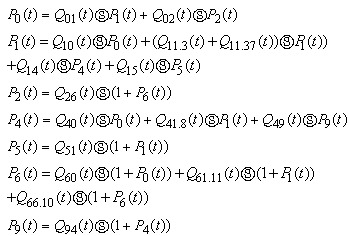
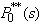 . The expected number of preventive maintenances per unit time are given by
. The expected number of preventive maintenances per unit time are given by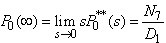
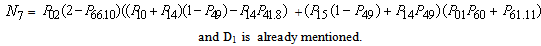
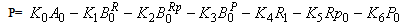 WhereK0 = Revenue per unit up-time of the system K1 = Cost per unit time for which server is busy due to repair K2 = Cost per unit time for which server is busy due to replacementK3 = Cost per unit time for which server is busy due to preventive maintenanceK4 = Cost per unit time repair K5 = Cost per unit time replacement K6 = Cost per unit time preventive maintenance
WhereK0 = Revenue per unit up-time of the system K1 = Cost per unit time for which server is busy due to repair K2 = Cost per unit time for which server is busy due to replacementK3 = Cost per unit time for which server is busy due to preventive maintenanceK4 = Cost per unit time repair K5 = Cost per unit time replacement K6 = Cost per unit time preventive maintenance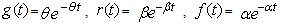 We can obtain the following results:
We can obtain the following results: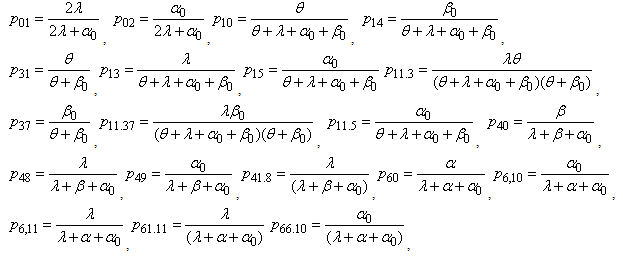 Also
Also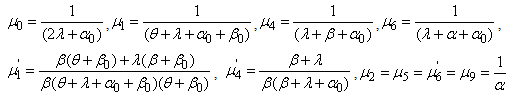 And
And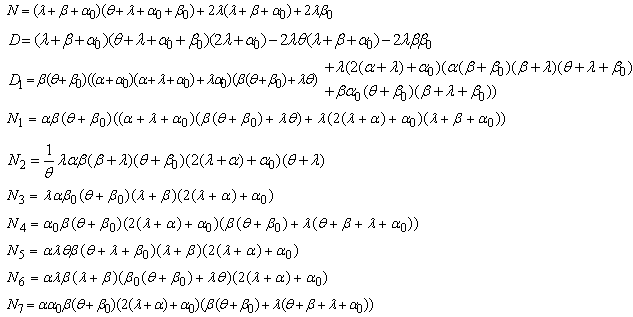



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML