-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(6): 421-427
doi:10.5923/j.ajms.20130306.17
On Bases in Banach Spaces
Hashimov Ch. M.
Ganja State University, Ganja, Azerbaijan
Correspondence to: Hashimov Ch. M., Ganja State University, Ganja, Azerbaijan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Some problems of bases in Banach spaces are considered. With the help of some complete and minimal system, a new Banach space is determined for which the given system forms a monotone basis. Some relations between the space of coefficients of this system and 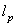 are established. Banach space generated by the Fourier coefficients of the functions from
are established. Banach space generated by the Fourier coefficients of the functions from 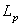 is also considered. The basis properties of the system of exponents in this space are studied. We also consider the example of an exponential bases in the weighted space on the real line.
is also considered. The basis properties of the system of exponents in this space are studied. We also consider the example of an exponential bases in the weighted space on the real line.
Keywords: Non-degenerate System, Basis, the Muckenhoupt Condition, an Exponential Bases
Cite this paper: Hashimov Ch. M., On Bases in Banach Spaces, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 421-427. doi: 10.5923/j.ajms.20130306.17.
Article Outline
1. Introduction
- The study of bases in different linear structures plays an important scientific and practical interest in many areas mathematics and natural science. There are numerous monographs as Singer I.[1;2], Day М.М.[3], Young R.[4], Heil Ch.[5], Christensen O.[6;7], Charles K. Chui[8] and others, and even review articles ( see e.g.[9]) devoted to them. From the point of view of applications recently interest in the study of various generalizations of bases (frames and their modifications) is increased. More details about related problems can be found in[4-8]. In this theory, the special role played the Banach space of sequences of scalars, including the space of coefficients having a canonical basis. In this paper in the term of the Banach space of coefficients generated by the non-degenerate system of some Banach space is considered. In the case of completeness and minimality of this system in above stated space (even if doesn’t form a basis), it is shown that it forms a basis for the obtained space. Some concrete examples are given. We also consider the example of an exponential bases in the weighted space on the real line.
2. Needful concepts and facts
- We will use the usual notations:
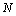 will be a set of all positive integers;
will be a set of all positive integers; 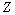 is the set of all integers;
is the set of all integers; 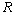 is the set of all real numbers;
is the set of all real numbers; 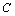 will stand for the field of complex numbers; Banach space will be referred to as
will stand for the field of complex numbers; Banach space will be referred to as 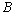 -space;
-space; 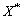 will stand for a space conjugated to
will stand for a space conjugated to 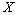 ;
; 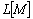 is a linear span of the set
is a linear span of the set 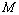 ;
; 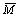 is a closure of the set
is a closure of the set 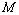 in the corresponding topology;
in the corresponding topology; 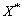 will stand for a space conjugated to
will stand for a space conjugated to 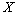 ;
; 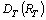 a domain of definition (a range of values) of the operator
a domain of definition (a range of values) of the operator 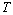 ;
; 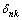 is the Kronecker symbol;
is the Kronecker symbol; 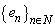 is canonical system, where
is canonical system, where 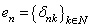 . We will need some concepts and facts from the theory of basis.Definition 1. System
. We will need some concepts and facts from the theory of basis.Definition 1. System 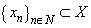 is called complete in
is called complete in 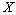 if
if 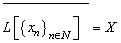 .Definition 2. System
.Definition 2. System 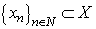 is called minimal in
is called minimal in 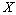 if
if 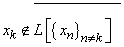 ,
, 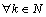 .The following criteria of completeness and minimality are available.Statement 1. System
.The following criteria of completeness and minimality are available.Statement 1. System 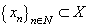 is complete in
is complete in 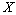 if and only if
if and only if 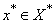 :
: 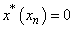 ,
, 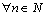 , implies
, implies 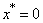 .Statement 2. System
.Statement 2. System 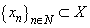 is minimal in
is minimal in 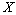 if and only if
if and only if 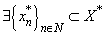 :
: 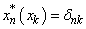 ,
, 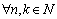 .Also recall the definition of a basis.Definition 3. System
.Also recall the definition of a basis.Definition 3. System 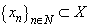 forms a basis for
forms a basis for 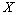 if
if 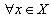
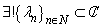 :
: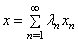 .Basicity criteria. The following basicity criteria of systems in
.Basicity criteria. The following basicity criteria of systems in 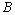 -spaces is true.Theorem 1. System
-spaces is true.Theorem 1. System 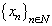 forms a basis for
forms a basis for 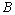 -space
-space 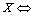 the following conditions are fulfilled:1)
the following conditions are fulfilled:1) 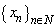 is complete in
is complete in 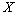 ;2)
;2) 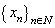 is minimal in
is minimal in 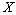 ;3) Projectors
;3) Projectors 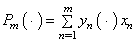 are uniformly bounded , i.e.
are uniformly bounded , i.e. 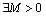 :
: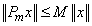 ,
, 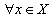 ,where
,where 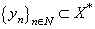 is an appropriate biorthogonal system to
is an appropriate biorthogonal system to 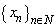 , and
, and 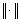 is a norm in
is a norm in 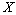 .Bases
.Bases 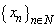 are called a monotone basis in
are called a monotone basis in 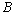 -space
-space 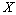 , if the following inequality holds
, if the following inequality holds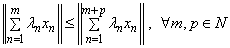 .Let
.Let 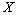 be some
be some 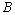 -space and
-space and 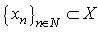 be minimal system with conjugate system
be minimal system with conjugate system 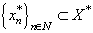 . Let
. Let 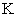 be some
be some 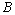 -space of sequences of scalars.If
-space of sequences of scalars.If 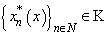 ,
, 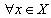 we will said that the system
we will said that the system 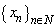 has
has 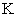 -property.
-property.3. Space 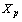
- Let
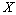 be
be 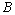 -space,
-space, 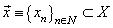 be complete and minimal with the conjugate system
be complete and minimal with the conjugate system 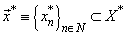 in it. Assume
in it. Assume 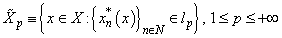 .It is easy to see that
.It is easy to see that 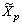 is a normed space with a norm
is a normed space with a norm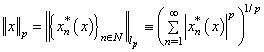
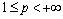 ,
,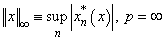 .The completion of
.The completion of 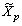 with respect to the norm
with respect to the norm 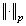 will be denoted by
will be denoted by 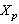 . We have
. We have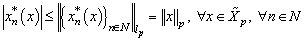 .Hence it directly follows that the functional
.Hence it directly follows that the functional 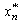 is bounded on
is bounded on 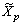 , for
, for 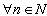 and its extension by continuity on
and its extension by continuity on 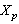 denote by
denote by 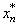 . Thus,
. Thus, 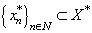 . From
. From 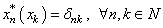 , follows that the system
, follows that the system 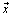 is minimal in
is minimal in 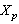 . Consider the projectors
. Consider the projectors 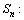
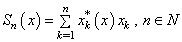 .We have
.We have 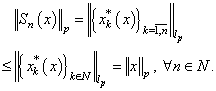 Consequently, the family
Consequently, the family 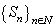 is uniformly bounded in
is uniformly bounded in 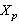 . Completeness of the system
. Completeness of the system 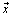 in
in 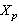 is obvious. Then from the basicity criteria we obtain the validity of the following theorem.Theorem 2. Let
is obvious. Then from the basicity criteria we obtain the validity of the following theorem.Theorem 2. Let 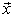 be complete and minimal system in
be complete and minimal system in 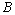 -space
-space 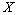 ,
, 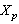 be
be 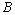 -space with a norm
-space with a norm 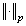 generated by
generated by 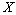 ,
, 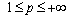 . Then this system forms a monotone basis for
. Then this system forms a monotone basis for 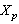 .Indeed, the fact that the system
.Indeed, the fact that the system 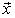 forms a basis for
forms a basis for 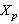 , is proved. It is easy to see that it holds
, is proved. It is easy to see that it holds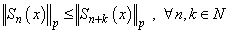 .Consequently, the system
.Consequently, the system 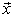 forms a monotone basis for
forms a monotone basis for 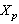 . Consider the operator
. Consider the operator 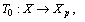
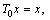
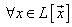 . It is clear that
. It is clear that 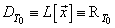 .
. 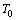 is an invertible operator, since
is an invertible operator, since 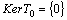 . Let
. Let 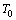 be bounded on
be bounded on 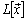 , i.e.
, i.e. 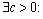
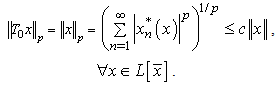 | (1) |
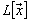 is a dense in
is a dense in 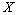 , continuing the operator
, continuing the operator 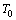 of the continuity from (1) we obtain
of the continuity from (1) we obtain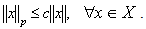 | (2) |
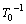 is bounded, then holds
is bounded, then holds 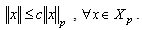 | (3) |
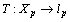 , defined by the expression
, defined by the expression 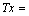
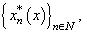
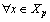 . Consequently,
. Consequently, 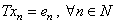 , where
, where 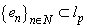 is a canonical system. We have
is a canonical system. We have 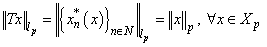 .It is clear that if the system
.It is clear that if the system 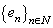 is complete in
is complete in 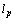 , then the operator
, then the operator 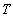 provides an isometric isomorphism between
provides an isometric isomorphism between 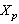 and
and 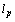 . Consequently, for
. Consequently, for 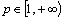 , the spaces
, the spaces 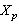 and
and 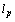 are isomorphic. Assume that the spaces
are isomorphic. Assume that the spaces 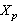 and
and 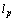 are isomorphic and the inequalities (2), (3) hold. Then it is easy to see that the operator
are isomorphic and the inequalities (2), (3) hold. Then it is easy to see that the operator 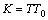 provides an isomorphism between
provides an isomorphism between 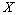 and
and 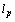 , moreover,
, moreover, 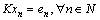 . Consequently, in this case the system
. Consequently, in this case the system 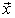 forms a basis for
forms a basis for 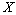 and its space of coefficients
and its space of coefficients 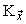 coincides with the space
coincides with the space 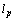 . Isomorphism between the spaces
. Isomorphism between the spaces 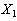 and
and 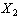 will be denoted as
will be denoted as 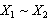 . So, let
. So, let 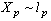 , i.e.
, i.e. 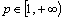 and the inequality (2) holds. Hence,
and the inequality (2) holds. Hence, 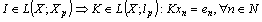 . Then by the results of[10] we obtain that the system
. Then by the results of[10] we obtain that the system 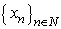 has
has 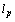 -property. Conversely, if the inequality (3) holds, then according to the results of[10], the system
-property. Conversely, if the inequality (3) holds, then according to the results of[10], the system 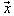 is
is 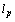 -system in
-system in 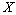 . Thus, if the inequality (2) holds, then
. Thus, if the inequality (2) holds, then 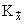
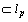 , if the inequality (3), then conversely,
, if the inequality (3), then conversely, 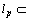
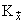 . As a result, we obtain the validity of the following theorem.Theorem 3. Let
. As a result, we obtain the validity of the following theorem.Theorem 3. Let 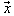 be complete and minimal system in
be complete and minimal system in 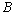 -space
-space 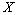 ,
, 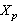 be
be 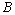 - space generated by
- space generated by 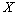 ,
, 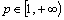 . Then
. Then 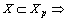
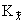
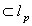 , and
, and 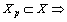
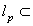
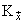 . If
. If 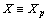 , then it is clear that
, then it is clear that 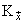
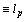 and
and 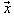 forms a basis for
forms a basis for 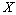 .
.4. Space 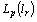
- Let
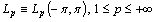 , be an ordinary Lebesgue space of functions. We denote by
, be an ordinary Lebesgue space of functions. We denote by 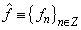 , the Fourier transform of the function
, the Fourier transform of the function 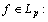
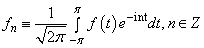 .Let
.Let 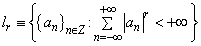 . Put
. Put 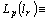
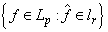 , where
, where 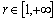 is some number and accept the norm
is some number and accept the norm 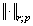 in
in 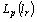 :
: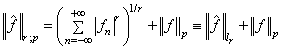 ,where
,where 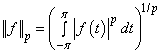 . It is clear that
. It is clear that 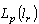 is the normalized, linear space. We show that it is Banach space too. Let
is the normalized, linear space. We show that it is Banach space too. Let 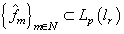 be some fundamental sequence:
be some fundamental sequence: 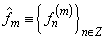 ,
, 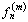 be Fourier coefficient of functions
be Fourier coefficient of functions 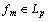 . From the completeness of space
. From the completeness of space 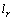 follows that
follows that 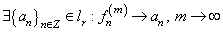 . On the other hand, from the evaluation of
. On the other hand, from the evaluation of 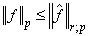 , it directly follows that
, it directly follows that 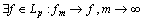 . It is easy to see that
. It is easy to see that 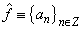 and
and 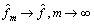 in
in 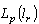 . Take
. Take 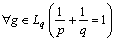 and consider the functional
and consider the functional 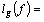
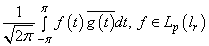 .It is easy to see that
.It is easy to see that 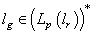 , as a result,
, as a result, 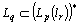 and the function in
and the function in 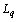 we will identify with the corresponding functionals. It is clear that, the system
we will identify with the corresponding functionals. It is clear that, the system 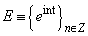 is a system biorthogonal to
is a system biorthogonal to 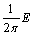 in
in 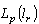 .Consider the completeness of the system
.Consider the completeness of the system 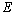 in
in 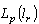 . First, consider the case
. First, consider the case 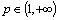 . In this case the system
. In this case the system 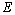 forms a basis for
forms a basis for 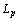 . Take
. Take 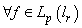 . Let
. Let 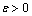 be an arbitrary number. It is obvious that
be an arbitrary number. It is obvious that 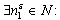
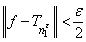 , where
, where 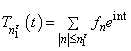 . On the other hand
. On the other hand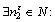
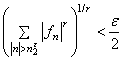 . Put
. Put 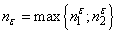 and assume
and assume 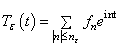 . We have
. We have 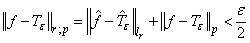
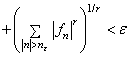 .This immediately implies the completeness of the system
.This immediately implies the completeness of the system 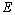 in
in 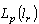 . Consider the projectors
. Consider the projectors 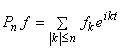 .
.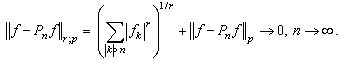 Consequently, the system
Consequently, the system 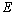 forms a basis for
forms a basis for 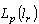 ,
, 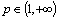 .Consider the case
.Consider the case 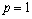 . It is obvious that
. It is obvious that 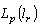 is continuously embedded in
is continuously embedded in 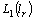 , i.e.
, i.e. 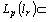
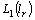 ,
, 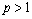 . As a result
. As a result 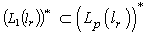 . Let the functional
. Let the functional 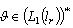 cancels out the system
cancels out the system 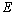 . Since
. Since 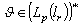 and
and 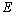 forms a basis for
forms a basis for 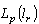 , then it is clear that
, then it is clear that 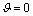 . Thus, the following theorem is true. Theorem 4. System
. Thus, the following theorem is true. Theorem 4. System 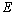 forms a basis for
forms a basis for 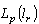 if
if  ; is complete and minimal in it if
; is complete and minimal in it if 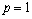 ,
, 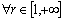 .Separately, we consider the case
.Separately, we consider the case 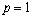 . Let
. Let 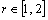 . By Statement 1 implies the system
. By Statement 1 implies the system 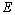 is complete and minimal in
is complete and minimal in 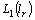 . Take
. Take 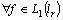 . Consequently,
. Consequently, 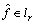 . Hence,
. Hence, 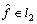 , and
, and 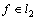 . Consider the partial sums
. Consider the partial sums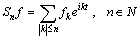 .We have
.We have 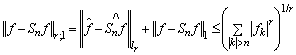
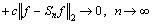 ,where
,where 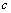 is an absolute constant. So the following theorem is true. Theorem 5. The system of exponents forms a basis for
is an absolute constant. So the following theorem is true. Theorem 5. The system of exponents forms a basis for 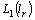 , for
, for 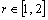 .It is absolutely clear that
.It is absolutely clear that 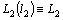 .
.5. On exponential Bases in 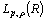
5.1. Abstract Case
- Let
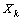
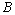 -space with a norm
-space with a norm 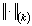 ,
, 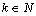 . Assume
. Assume 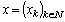 ,
, 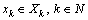 . Let us define linear operations of addition and multiplication by scalars coordinate-wise. Define
. Let us define linear operations of addition and multiplication by scalars coordinate-wise. Define 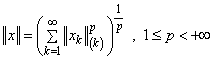 .We denote the obtained
.We denote the obtained 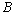 -space by
-space by 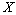 . It is absolutely clear that the subspace of the elements of the form
. It is absolutely clear that the subspace of the elements of the form 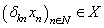 is isometrically isomorphic to
is isometrically isomorphic to 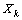 . Therefore, accurate to within an isometry, the direct expansion
. Therefore, accurate to within an isometry, the direct expansion 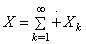 holds. Assume that the system
holds. Assume that the system 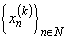 forms a basis for
forms a basis for 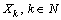 . Consider the system
. Consider the system 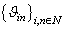 , where
, where 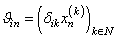 ,
, 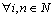 . It is obvious that
. It is obvious that 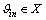 ,
, 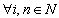 . Denote by
. Denote by  ,
, 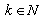 , the system biorthogonal to
, the system biorthogonal to 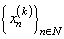 . Before proceeding with further considerations, we define the following space. Let
. Before proceeding with further considerations, we define the following space. Let 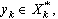
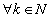 and
and 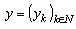 . Define the norm as follows.
. Define the norm as follows.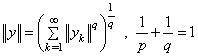 .We define the linear operations in a set of such elements coordinate-wise. Denote the obtained
.We define the linear operations in a set of such elements coordinate-wise. Denote the obtained 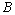 -space by
-space by 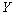 . Let us show that
. Let us show that 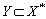 . Take
. Take 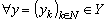 and define
and define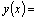
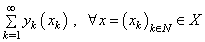 .We have
.We have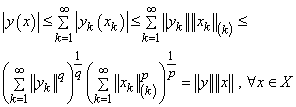 .It is clear that
.It is clear that 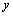 is a linear continuous functional on
is a linear continuous functional on 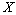 . Consequently,
. Consequently, 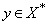 . Thus,
. Thus, 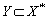 . Consider the system
. Consider the system 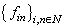 , where
, where 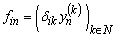 ,
, 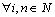 . It is clear that
. It is clear that 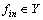 ,
, 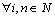 . We have
. We have 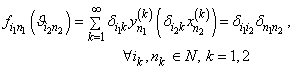 .Consequently,
.Consequently, 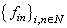 is a system biorthogonal to
is a system biorthogonal to 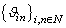 . Take
. Take 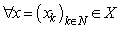 and consider partial sums
and consider partial sums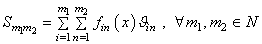 .We have
.We have 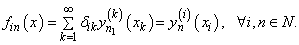 Taking into account an expression for the
Taking into account an expression for the 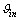 , we have
, we have 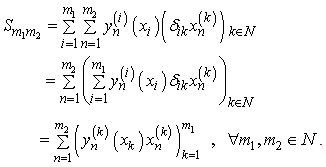 Hence
Hence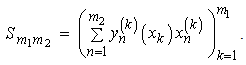 Since,
Since, 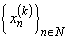 forms a basis for
forms a basis for 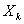 , passing to the limit as
, passing to the limit as 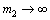 yields
yields 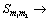
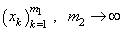 . In fact
. In fact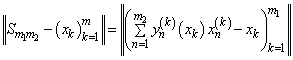
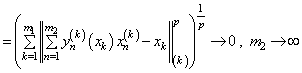 .As a result, we obtain
.As a result, we obtain 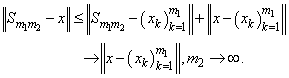 It is clear that
It is clear that 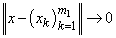 ,
, 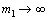 . Thus, the following theorem is true. Theorem 6. Let the system
. Thus, the following theorem is true. Theorem 6. Let the system 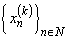 forms a basis for
forms a basis for 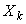 ,
,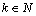 . Then the system
. Then the system 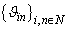 forms a basis for
forms a basis for 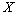 , where
, where 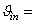
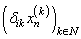 ,
, 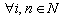 .
.5.2. 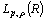 Realization
Realization
- Here we consider the realization of this approach on the example of the weighted Lebesgue space
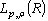 with the norm
with the norm 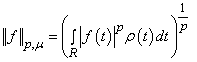 ,where
,where 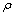 is some weight function. Let
is some weight function. Let 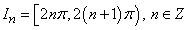 , and
, and 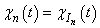 be a characteristic function on half-interval
be a characteristic function on half-interval 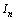 . Suppose
. Suppose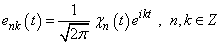 .Let us assume that the weight function
.Let us assume that the weight function 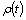 satisfies the Muckenhoupt condition[11]
satisfies the Muckenhoupt condition[11]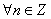 | (4) |
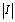 is a Lebesgue measure of the set
is a Lebesgue measure of the set 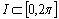 . Then the system of exponents
. Then the system of exponents 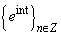 forms a basis for
forms a basis for 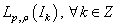 (see, e.g.[12-14]). The system biorthogonal to it has the form
(see, e.g.[12-14]). The system biorthogonal to it has the form 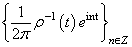 . Since the conjugate of
. Since the conjugate of 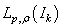 is identified with the space
is identified with the space 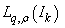 and the every functional
and the every functional 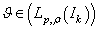 is related to the element
is related to the element 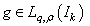 through
through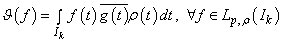 .Consequently,
.Consequently, 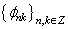 is a system biorthogonal to
is a system biorthogonal to 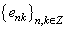 in
in 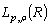 , where
, where 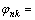
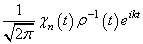 . Take
. Take 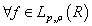 . Denote by
. Denote by 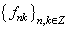 the biorthogonal coefficients of the function
the biorthogonal coefficients of the function 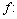
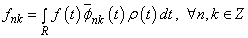 . Consider the partial sums
. Consider the partial sums 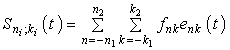 .
.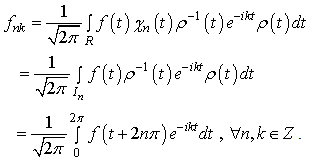 Taking into account the expression for
Taking into account the expression for 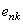 we obtain
we obtain 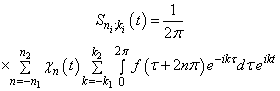 .We have
.We have 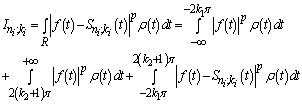 .Moreover
.Moreover 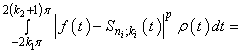
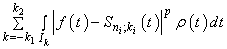 On the other hand
On the other hand 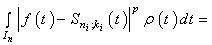
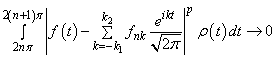 ,
,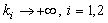 .As a result
.As a result 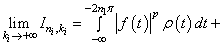
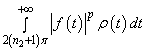 ,and, consequently
,and, consequently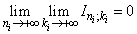 .Thus, the following theorem is true.Theorem 7. System
.Thus, the following theorem is true.Theorem 7. System 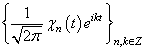 forms a basis for
forms a basis for 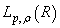 ,
, 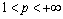 , if the function
, if the function 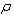 satisfies the Muckenhoupt condition (4).From this theorem we immediately obtainCorollary 1. System
satisfies the Muckenhoupt condition (4).From this theorem we immediately obtainCorollary 1. System 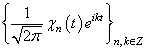 forms an orthonormal basis for
forms an orthonormal basis for 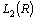 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML -Bessel and
-Bessel and  -Hilbert systems.
-Hilbert systems. 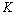 -bases. Dokl. RAN, 429(3), 1-3, 2009.
-bases. Dokl. RAN, 429(3), 1-3, 2009.