Taalaibek D. Omurov
Doctor of Physics and Mathematics, professor of Z. Balasagyn Kyrgyz National University, Bishkek, Kyrgyzstan
Correspondence to: Taalaibek D. Omurov, Doctor of Physics and Mathematics, professor of Z. Balasagyn Kyrgyz National University, Bishkek, Kyrgyzstan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Existence and conditional-smooth solution of the Navier-Stokes equation is one of the most important problems in mathematics of the century, which describes the motion of viscous Newtonian fluid and which is a basic of hydrodynamic [1]. Therefore in this work we solve a nonstationary problem Navier-Stokes for incompressible fluid.
Keywords:
Navier-Stokes, Problem, Conditional-smooth, Solution, Fluid, Flow, Viscosity, Convective the Acceleration, Differentiation, Algorithm, Newton’s Potential
Cite this paper: Taalaibek D. Omurov, Nonstationary Navier-Stokes Problem for Incompressible Fluid with Viscosity, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 349-356. doi: 10.5923/j.ajms.20130306.08.
1. Introduction
If to designate components of vectors of speed and external force, as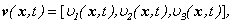
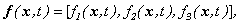 that for each value
that for each value 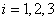 turns out the corresponding scalar equation of Navier-Stokes
turns out the corresponding scalar equation of Navier-Stokes 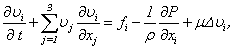 | (1.1) |
with conditions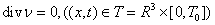 | (1.2) |
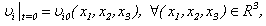 | (1.3) |
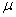 > 0 - kinematic viscosity,
> 0 - kinematic viscosity, 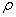 - density, Δ - Laplas’s operator. The additional equation is the condition incompressibility fluid (2). Unknown are speed
- density, Δ - Laplas’s operator. The additional equation is the condition incompressibility fluid (2). Unknown are speed 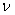 and pressure P.The work purpose. The main object of this work - existence and proofs of single and conditional smoothness of the decision of a problem Navier-Stokes for an incompressible fluid with viscosity.Theoretical and practical value. Our problem does not include a derivation of an equation in a physical meaning, since there is a big amount of works reflecting these questions [2-4, 8-10]. The Received decisions on the basis of the developed analytical methods proves in the general applicability of the equations of Navier-Stokes.In a case
and pressure P.The work purpose. The main object of this work - existence and proofs of single and conditional smoothness of the decision of a problem Navier-Stokes for an incompressible fluid with viscosity.Theoretical and practical value. Our problem does not include a derivation of an equation in a physical meaning, since there is a big amount of works reflecting these questions [2-4, 8-10]. The Received decisions on the basis of the developed analytical methods proves in the general applicability of the equations of Navier-Stokes.In a case 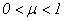 the current is considered with very small viscosity. When the current is considered with very small viscosity i.e. when Reynolds's number is very great
the current is considered with very small viscosity. When the current is considered with very small viscosity i.e. when Reynolds's number is very great 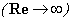 [8,9] there is an border layer in which viscosity influence is concentrated. In many works in this area of the decision of the equations Navier-Stokes received by the numerical analysis, also confirm these conclusions.And in a case
[8,9] there is an border layer in which viscosity influence is concentrated. In many works in this area of the decision of the equations Navier-Stokes received by the numerical analysis, also confirm these conclusions.And in a case 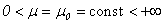 the current is considered with average size of viscosity. At very slow currents, or in currents of is strong-viscous liquids of force of a friction much more, than forces of inertia. Hence convective the acceleration doing the equations nonlinear, everywhere are supposed identically equally to a zero [9]. Therefore in a case when convective acceleration is not equal to zero problems connected with methods of integration of the equations of Navier-Stokes in their general view are arisen.The decision of many problems of theoretical and mathematical physics leads to use of various special weight spaces. In works [5-7] for the first time have offered a method which gives solution of problem Navier-Stokes in
the current is considered with average size of viscosity. At very slow currents, or in currents of is strong-viscous liquids of force of a friction much more, than forces of inertia. Hence convective the acceleration doing the equations nonlinear, everywhere are supposed identically equally to a zero [9]. Therefore in a case when convective acceleration is not equal to zero problems connected with methods of integration of the equations of Navier-Stokes in their general view are arisen.The decision of many problems of theoretical and mathematical physics leads to use of various special weight spaces. In works [5-7] for the first time have offered a method which gives solution of problem Navier-Stokes in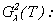
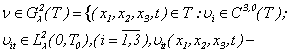 is continuous and limited functions on
is continuous and limited functions on 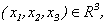
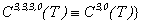 and
and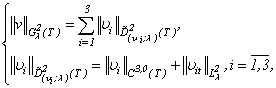 | (1.4) |
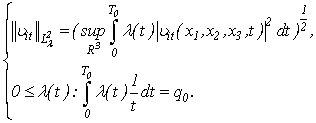 To answer the brought attention to the question, we offer the following method of the decision of a problem Navier-Stokes . For that the phrpose, system (1.1) we will transform to a kind
To answer the brought attention to the question, we offer the following method of the decision of a problem Navier-Stokes . For that the phrpose, system (1.1) we will transform to a kind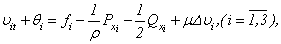 | (1.5) |
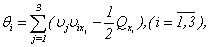 | (1.6) |
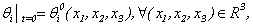 | (1.7) |
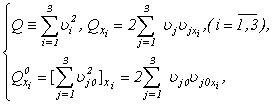 | (1.8) |
without breaking equivalence of system (1.1) and (1.5), (1.6). The received systems (1.5), (1.6) contain unknown persons 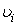 ,
, 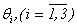 and pressure P. Here
and pressure P. Here 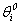 - known functions because are known
- known functions because are known 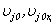 .The developed method of the decision of systems (1.5) and (1.6), is connected with functions
.The developed method of the decision of systems (1.5) and (1.6), is connected with functions 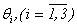 , i.e.A)
, i.e.A) 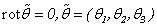 ;
;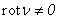 or B)
or B) 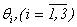 - any functions if, accordingly, as necessary conditions, take place: а0)
- any functions if, accordingly, as necessary conditions, take place: а0) 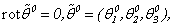 b0)
b0) 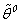 - any functions.
- any functions.
2. A Problem of Navier-Stokes with a Condition (А)
In this paragraph in the subsequent points, at the specified restrictions on the entrance data, the strict substantiation of compatibility of systems (1.5), (1.6) will be given.
2.1. Research With a Condition (A)
Let functions 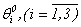 satisfy to a condition (a0). Then relatively
satisfy to a condition (a0). Then relatively 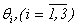 we suppose a condition (A) and
we suppose a condition (A) and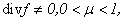 | (2.1) |
where from system (1.5) and (1.6), accordingly we will receive following systems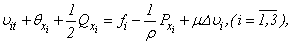 | (2.2) |
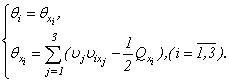 | (2.3) |
Theorem 1. Let conditions (1.2), (1.3), (A) and (2.1) are satisfied. Then systems (2.2) and (2.3) it is equivalent will be transformed to a kind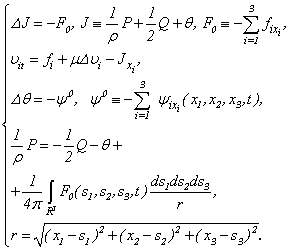 | (2.4) |
Hence, the problem (1.1) - (1.3) has the unique decision which satisfies to a condition (1.2).Proof. From system (2.2) it is visible, if the 1-equation (2.2, i=1) it is differentiated on x1, 2-equation on x2 (2.2, i=2), 3-equation on x3 (2.2, i=3), and it is summarised, we will receive the equation of Puasson [10] 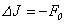 | (2.5) |
as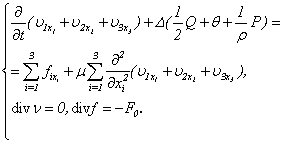 At that it is proved
At that it is proved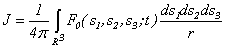 | (2.6) |
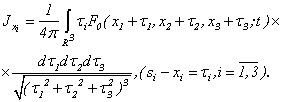 | (2.7) |
Algorithm when we will receive the equation of Puasson (2.5) for brevity we name «algorithm puassonization systems».In work of Sobolev [10] it is specified that function (2.6) satisfies to the equation (2.5) and is called Newtons’ potential.Therefore, if J - the decision of the equation (2.5), then substituting 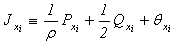 | (2.8) |
in (2.2), we have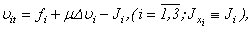 | (2.9) |
i.e. system (2.2) it is equivalent by (2.9) will be transformed to a kind linear the nonuniform equation of heat conductivity. The equations (2.5), (2.9) is there are first and second equations of system (2.4).The system (2.9) is solved by S.L.Sobolev’s method: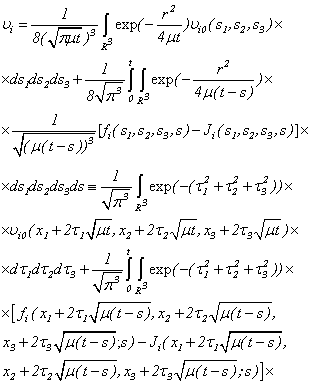
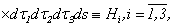 | (2.10) |
where 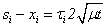 or
or 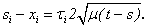 All
All 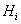 - is known functions and
- is known functions and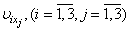 are defined from system (2.10):
are defined from system (2.10):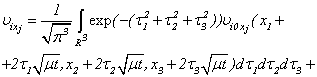
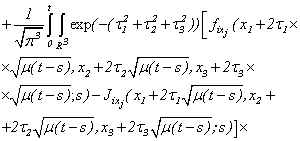
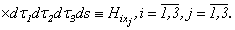 | (2.11) |
Then, on the basis of (2.3), (2.10) and (2.11), and their private derivatives on xi, we find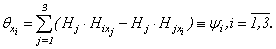 | (2.12) |
As 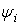 - is known functions, hence from system (2.12) differentiating 1 equation on x1 [(2.12): i=1 ], 2 equations on х2 [(2.12): i=2 ], 3 equations on х3 [(2.12): i=3 ], and summarising, we will receive
- is known functions, hence from system (2.12) differentiating 1 equation on x1 [(2.12): i=1 ], 2 equations on х2 [(2.12): i=2 ], 3 equations on х3 [(2.12): i=3 ], and summarising, we will receive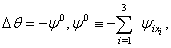 | (2.13) |
at that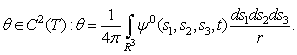 The equation (2.13) is the third equation of system (2.4). Therefore, from the received results, taking into account (2.6), follows
The equation (2.13) is the third equation of system (2.4). Therefore, from the received results, taking into account (2.6), follows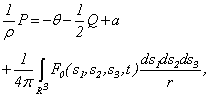 | (2.14) |
i.e. functions  are defined from systems (2.10), (2.13), (2.14).Uniqueness is obvious, as a method by contradiction from (2.10) uniqueness of the decision follows
are defined from systems (2.10), (2.13), (2.14).Uniqueness is obvious, as a method by contradiction from (2.10) uniqueness of the decision follows 
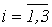 . Results (2.10) with a condition ((A), (2.1)) are received where smoothness of functions
. Results (2.10) with a condition ((A), (2.1)) are received where smoothness of functions 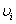 is required only on xi as the derivative of 1st order in time has feature in t=0. Then taking into account (2.10), (2.13), (2.14) and the system (2.4) has the unique continuous decision.Further, considering private derivatives of 1st order
is required only on xi as the derivative of 1st order in time has feature in t=0. Then taking into account (2.10), (2.13), (2.14) and the system (2.4) has the unique continuous decision.Further, considering private derivatives of 1st order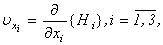 | (2.15) |
and summarising (2.15) with taking into account (1.2), we have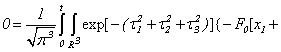
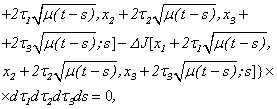 as
as 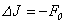 .Means, the system (2.10) satisfies to the equation (1.2).
.Means, the system (2.10) satisfies to the equation (1.2).
2.2. Limitation of Functions 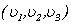 in
in 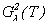
The limiting case which we will consider concerns results of the theorem 1. Then the decision of system (1.1) is representing in the form of (2.10) with conditions (1.2), (1.3), (A), (2.1) and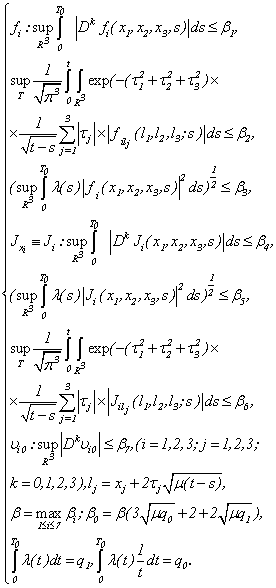 | (2.16) |
Really, estimating (2.10) in 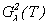 ,we have
,we have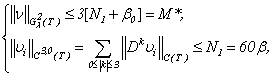
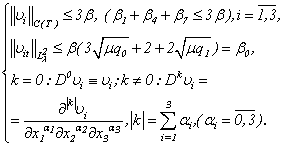 | (2.17) |
Theorem 2. In the conditions of the theorem 1 and (2.16), (2.17) the problem (1.1) - (1.3) has the unique decision in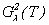 .
.
3. The Decision of a Problem of Navier-Stokes with a Condition (B)
Here we investigate a case (B) when 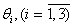 containing convective members of a problem of Navier-Stokes are any. Results of the theorem 1 are not applicable.Therefore, for the decision of a problem (1.1) - (1.3) we offer following algorithms.
containing convective members of a problem of Navier-Stokes are any. Results of the theorem 1 are not applicable.Therefore, for the decision of a problem (1.1) - (1.3) we offer following algorithms.
3.1. Problem Navier- Stokes with Average Viscosity
Let conditions (1.2), (1.3) are satisfied and: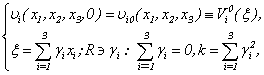 | (3.1) |
at that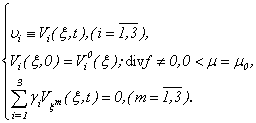 | (3.2) |
Then on the basis of functions 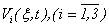 and
and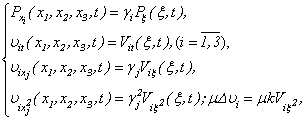 system (1.1) it is equivalent will be transformed to a kind
system (1.1) it is equivalent will be transformed to a kind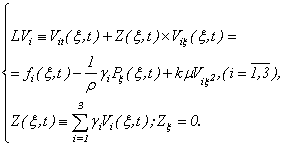 | (3.3) |
In the specified systems unknown persons contain 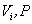 .Remark 1. Under regular in
.Remark 1. Under regular in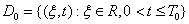 the decision we understand the decision
the decision we understand the decision 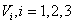 the equation (1.1) in
the equation (1.1) in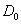 , which has a continuous derivative on
, which has a continuous derivative on 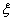 to the third order inclusive and continuous derivative on t(t>0). From system (3.3), considering conditions (3.2), and having entered «algorithm puassonization systems», i.e. differentiating the equations of system (3.3)
to the third order inclusive and continuous derivative on t(t>0). From system (3.3), considering conditions (3.2), and having entered «algorithm puassonization systems», i.e. differentiating the equations of system (3.3) 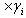 accordingly on
accordingly on 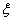 and, then summarising, we have the equation:
and, then summarising, we have the equation: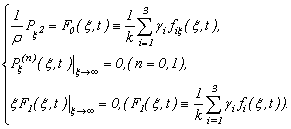 | (3.4) |
Therefore, we will receive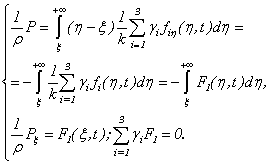 | (3.5) |
Really on a basis [(3.3): 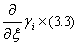 ], we have
], we have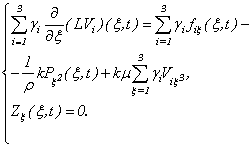 Then we have the following (3.4). Further, we have
Then we have the following (3.4). Further, we have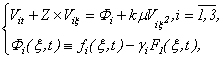 | (3.6) |
or for consideration of unknown functions 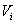 we have
we have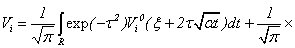
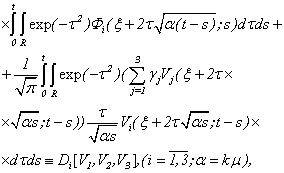 | (3.7) |
as here consider a method integration in parts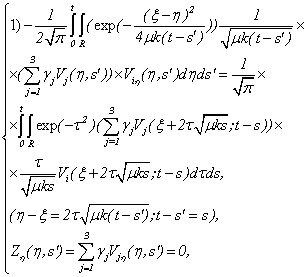 and
and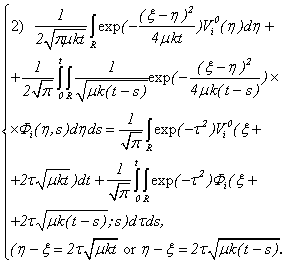 If functions
If functions 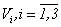 are system decisions (3.7) thus takes place (3.2) and
are system decisions (3.7) thus takes place (3.2) and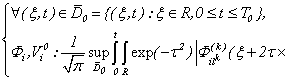
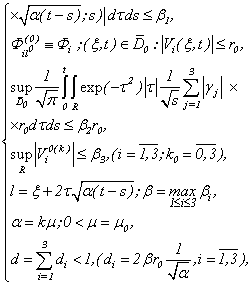 | (3.8) |
that 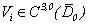 :
: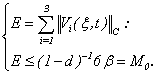 | (3.9) |
Then the solution of this system (3.7) we can find on the basis of Pikard’s method 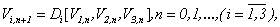 | (3.10) |
where 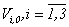 - initial estimates and at that
- initial estimates and at that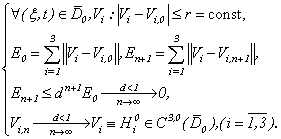 | (3.11) |
Theorem 3. Under conditions (2), (3), (3.2), (3.8) problem Navier-Stokes has the unique continuous decision.Definition 1. The generalised decision a problems (1.1)-(1.3), (3.2) in area 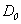 we name any continuous in
we name any continuous in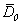 equation decision (3.7), when
equation decision (3.7), when 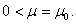
3.2. We will Consider a Fluid with Very Small Viscosity
Let conditions (1.2), (1.3), (3.1) are satisfied and: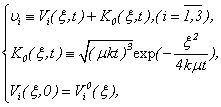
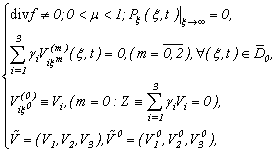 | (3.12) |
at that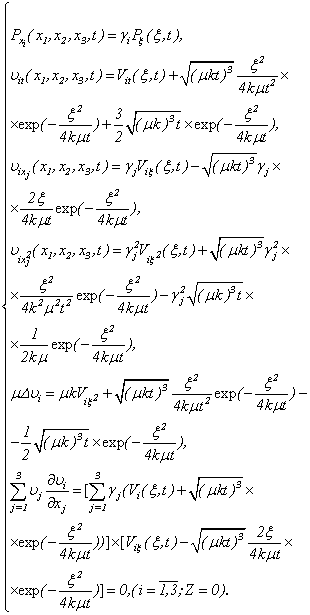 Then on the basis of functions
Then on the basis of functions 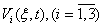 , system (1.1) it is equivalent will be transformed to a kind:
, system (1.1) it is equivalent will be transformed to a kind: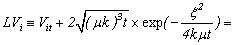
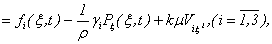 | (3.13) |
in the specified systems unknown persons contain 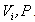 Therefore
Therefore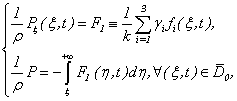 | (3.14) |
as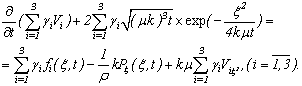 Theorem 4. Let functions are system decisions
Theorem 4. Let functions are system decisions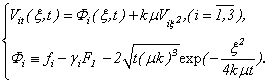 | (3.15) |
Then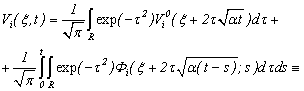
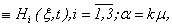 | (3.16) |
where known functions and 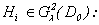
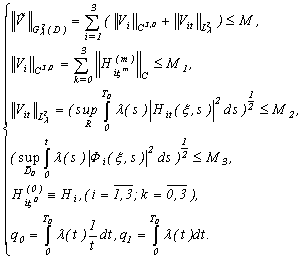 Theorem 5. If functions
Theorem 5. If functions 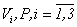 are system decisions (3.14), (3.15), (3.10) that (3.1) is the decision of system (1.1) in
are system decisions (3.14), (3.15), (3.10) that (3.1) is the decision of system (1.1) in 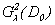 :
: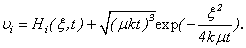 | (3.17) |
Remark 2. In particular, if conditions (1.2), (1.3), (3.12) and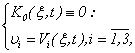 | (3.18) |
are satisfied. Then takes place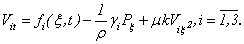 | (3.19) |
From here, considering (3.14), (3.15) we have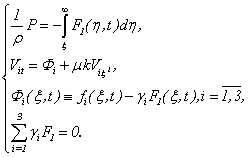 | (3.20) |
Hence all conditions of the theorem 4 and 5 are satisfied.Example 1. The specified method of the theorem 5 can be used in par ticular and for the decision on a problem (1.1)-(1.3) as a test example, when takes place: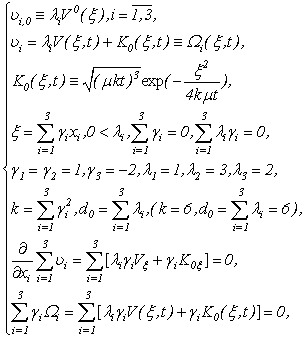 that
that 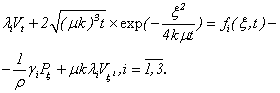 | (3.21) |
or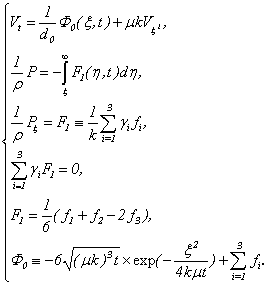 Then
Then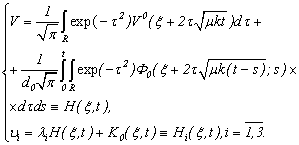 Remark 3. As
Remark 3. As 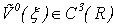 , that limitedly the decision of a problem of Navier-Stokes (1.1) - (1.3) with a condition (B) it is possible to prove limitation and in
, that limitedly the decision of a problem of Navier-Stokes (1.1) - (1.3) with a condition (B) it is possible to prove limitation and in 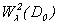 - weight space of type of Sobolev:
- weight space of type of Sobolev: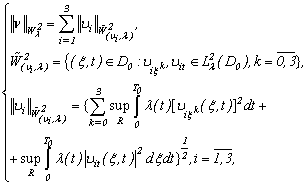 as
as 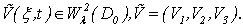
4. Conclusions
I. From the received results follows that system Navier-Stokes (1.1) in the conditions of (1.2), (1.3), (A1)-(A3) can have the analytical unique is conditional-smooth decision. At least, such decision answers to a mathematical question, and possibility to construct the decision of a problem of Navier-Stokes (1.1)-(1.3) for an incompressible liquid with viscosity.II. Results of the theorem 1 and 5 can be applied to a problem of Navier-Stokes of an incompressible fluid with viscosity, when 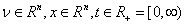 .
.
References
| [1] | Navier-Stokes Existence and Smoothness Problem//The Millennium Problems, stated in 2000 by Clay Mathematics Institute. |
| [2] | G. Birkhoff, (1983), Numerical fluid dynamics. SIAM Rev., Vol.25, No1, pp.1-34. |
| [3] | B.J. Cantwell, (1981), Organized motion in turbulent flow. Ann. Rev. Fluid Mech. Vol.13, pp.457-515. |
| [4] | Ladyzhensky Island And, (1970), Mathematical questions of dynamics of a viscous incompressible liquid. - Moscow: Science, 288 p. |
| [5] | T.D. Omurov, (2011), Nonstationary Navier-Stokes Problem for Incompressible Fluid (in Russian) //Mathematical morphology. Electronic mathemat. and the mediko-biologist magazine. X. – Release 1. - Identification №0421100004\0001.http://www.smolensk.ru/user/sgma/MMORHORPH/N-29-html/TITL-29.htm. |
| [6] | T.D. Omurov, (2010), Nonstationary Navier-Stokes Problem for Incompressible Fluid (in Russian). - J.Balasagyn KNU, Bishkek, 21p. |
| [7] | T.D.Omurov, (2013), Navier-Stokes problem for Incompressible fluid with viscosity//Varia Informatica 2013. Ed. M.Milosz, PIPS Polish Lublin, pp.137-158. |
| [8] | L. Prantdl, (1961), Gesammelte Abhandlungen zur angewandten Mechanik, Hudro- und Aerodynamic. Springer, Berlin. |
| [9] | H. Schlichting’s, (1974), Boundary-Layer Theory. Moscow: Science, 712 p. |
| [10] | L.S. Sobolev, (1966), Equations of Mathematical Physics. - Publ. 4. Moscow: Science, 443 p. |

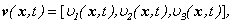
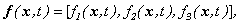 that for each value
that for each value 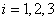 turns out the corresponding scalar equation of Navier-Stokes
turns out the corresponding scalar equation of Navier-Stokes 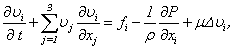
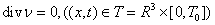
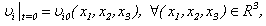
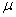 > 0 - kinematic viscosity,
> 0 - kinematic viscosity, 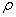 - density, Δ - Laplas’s operator. The additional equation is the condition incompressibility fluid (2). Unknown are speed
- density, Δ - Laplas’s operator. The additional equation is the condition incompressibility fluid (2). Unknown are speed 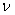 and pressure P.The work purpose. The main object of this work - existence and proofs of single and conditional smoothness of the decision of a problem Navier-Stokes for an incompressible fluid with viscosity.Theoretical and practical value. Our problem does not include a derivation of an equation in a physical meaning, since there is a big amount of works reflecting these questions [2-4, 8-10]. The Received decisions on the basis of the developed analytical methods proves in the general applicability of the equations of Navier-Stokes.In a case
and pressure P.The work purpose. The main object of this work - existence and proofs of single and conditional smoothness of the decision of a problem Navier-Stokes for an incompressible fluid with viscosity.Theoretical and practical value. Our problem does not include a derivation of an equation in a physical meaning, since there is a big amount of works reflecting these questions [2-4, 8-10]. The Received decisions on the basis of the developed analytical methods proves in the general applicability of the equations of Navier-Stokes.In a case 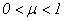 the current is considered with very small viscosity. When the current is considered with very small viscosity i.e. when Reynolds's number is very great
the current is considered with very small viscosity. When the current is considered with very small viscosity i.e. when Reynolds's number is very great 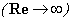 [8,9] there is an border layer in which viscosity influence is concentrated. In many works in this area of the decision of the equations Navier-Stokes received by the numerical analysis, also confirm these conclusions.And in a case
[8,9] there is an border layer in which viscosity influence is concentrated. In many works in this area of the decision of the equations Navier-Stokes received by the numerical analysis, also confirm these conclusions.And in a case 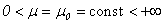 the current is considered with average size of viscosity. At very slow currents, or in currents of is strong-viscous liquids of force of a friction much more, than forces of inertia. Hence convective the acceleration doing the equations nonlinear, everywhere are supposed identically equally to a zero [9]. Therefore in a case when convective acceleration is not equal to zero problems connected with methods of integration of the equations of Navier-Stokes in their general view are arisen.The decision of many problems of theoretical and mathematical physics leads to use of various special weight spaces. In works [5-7] for the first time have offered a method which gives solution of problem Navier-Stokes in
the current is considered with average size of viscosity. At very slow currents, or in currents of is strong-viscous liquids of force of a friction much more, than forces of inertia. Hence convective the acceleration doing the equations nonlinear, everywhere are supposed identically equally to a zero [9]. Therefore in a case when convective acceleration is not equal to zero problems connected with methods of integration of the equations of Navier-Stokes in their general view are arisen.The decision of many problems of theoretical and mathematical physics leads to use of various special weight spaces. In works [5-7] for the first time have offered a method which gives solution of problem Navier-Stokes in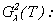
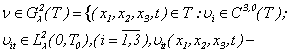 is continuous and limited functions on
is continuous and limited functions on 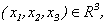
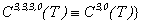 and
and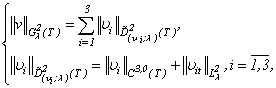
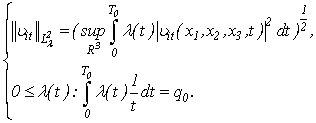 To answer the brought attention to the question, we offer the following method of the decision of a problem Navier-Stokes . For that the phrpose, system (1.1) we will transform to a kind
To answer the brought attention to the question, we offer the following method of the decision of a problem Navier-Stokes . For that the phrpose, system (1.1) we will transform to a kind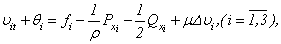
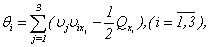
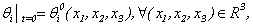
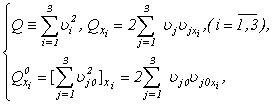
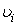 ,
, 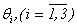 and pressure P. Here
and pressure P. Here 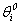 - known functions because are known
- known functions because are known 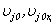 .The developed method of the decision of systems (1.5) and (1.6), is connected with functions
.The developed method of the decision of systems (1.5) and (1.6), is connected with functions 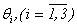 , i.e.A)
, i.e.A) 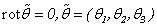 ;
;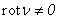 or B)
or B) 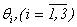 - any functions if, accordingly, as necessary conditions, take place: а0)
- any functions if, accordingly, as necessary conditions, take place: а0) 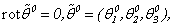 b0)
b0) 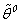 - any functions.
- any functions.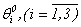 satisfy to a condition (a0). Then relatively
satisfy to a condition (a0). Then relatively 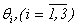 we suppose a condition (A) and
we suppose a condition (A) and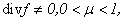
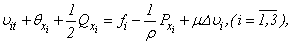
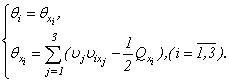
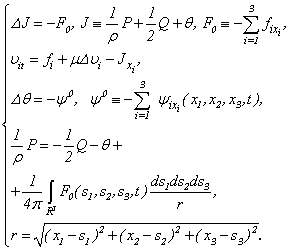
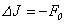
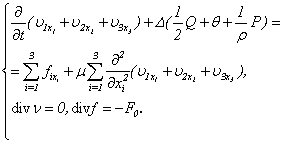 At that it is proved
At that it is proved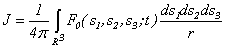
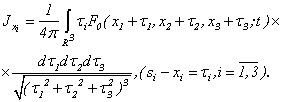
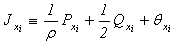
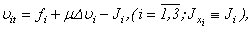
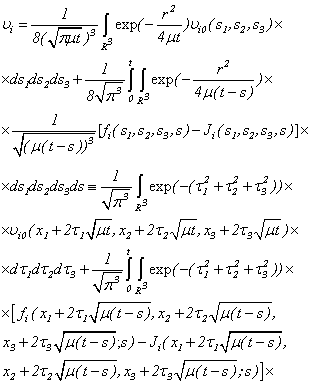
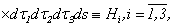
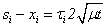 or
or 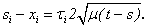 All
All 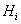 - is known functions and
- is known functions and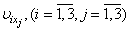 are defined from system (2.10):
are defined from system (2.10):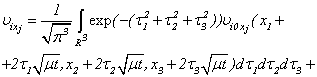
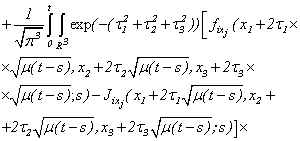
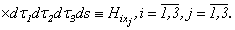
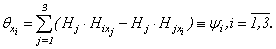
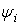 - is known functions, hence from system (2.12) differentiating 1 equation on x1 [(2.12): i=1 ], 2 equations on х2 [(2.12): i=2 ], 3 equations on х3 [(2.12): i=3 ], and summarising, we will receive
- is known functions, hence from system (2.12) differentiating 1 equation on x1 [(2.12): i=1 ], 2 equations on х2 [(2.12): i=2 ], 3 equations on х3 [(2.12): i=3 ], and summarising, we will receive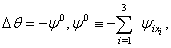
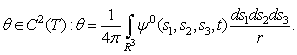 The equation (2.13) is the third equation of system (2.4). Therefore, from the received results, taking into account (2.6), follows
The equation (2.13) is the third equation of system (2.4). Therefore, from the received results, taking into account (2.6), follows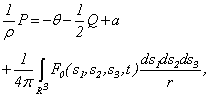
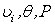 are defined from systems (2.10), (2.13), (2.14).Uniqueness is obvious, as a method by contradiction from (2.10) uniqueness of the decision follows
are defined from systems (2.10), (2.13), (2.14).Uniqueness is obvious, as a method by contradiction from (2.10) uniqueness of the decision follows 
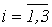 . Results (2.10) with a condition ((A), (2.1)) are received where smoothness of functions
. Results (2.10) with a condition ((A), (2.1)) are received where smoothness of functions 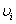 is required only on xi as the derivative of 1st order in time has feature in t=0. Then taking into account (2.10), (2.13), (2.14) and the system (2.4) has the unique continuous decision.Further, considering private derivatives of 1st order
is required only on xi as the derivative of 1st order in time has feature in t=0. Then taking into account (2.10), (2.13), (2.14) and the system (2.4) has the unique continuous decision.Further, considering private derivatives of 1st order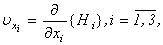
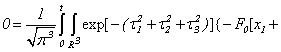
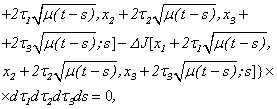 as
as 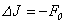 .Means, the system (2.10) satisfies to the equation (1.2).
.Means, the system (2.10) satisfies to the equation (1.2).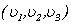 in
in 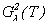
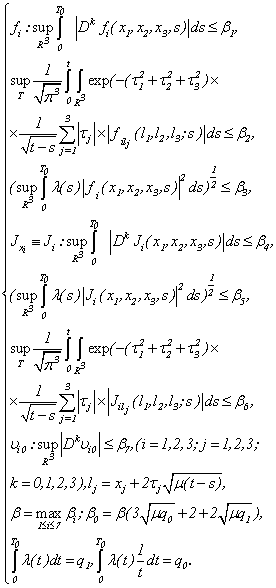
 ,we have
,we have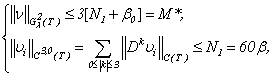
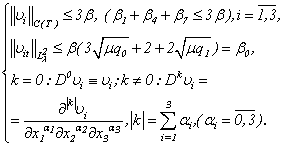
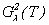 .
.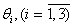 containing convective members of a problem of Navier-Stokes are any. Results of the theorem 1 are not applicable.Therefore, for the decision of a problem (1.1) - (1.3) we offer following algorithms.
containing convective members of a problem of Navier-Stokes are any. Results of the theorem 1 are not applicable.Therefore, for the decision of a problem (1.1) - (1.3) we offer following algorithms.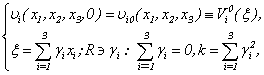
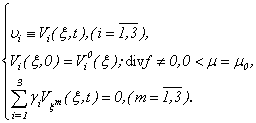
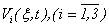 and
and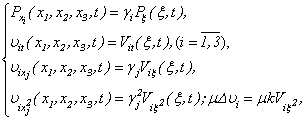 system (1.1) it is equivalent will be transformed to a kind
system (1.1) it is equivalent will be transformed to a kind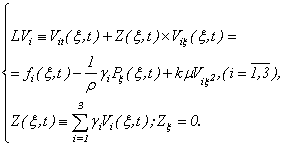
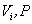 .Remark 1. Under regular in
.Remark 1. Under regular in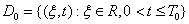 the decision we understand the decision
the decision we understand the decision 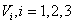 the equation (1.1) in
the equation (1.1) in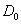 , which has a continuous derivative on
, which has a continuous derivative on 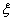 to the third order inclusive and continuous derivative on t(t>0). From system (3.3), considering conditions (3.2), and having entered «algorithm puassonization systems», i.e. differentiating the equations of system (3.3)
to the third order inclusive and continuous derivative on t(t>0). From system (3.3), considering conditions (3.2), and having entered «algorithm puassonization systems», i.e. differentiating the equations of system (3.3) 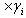 accordingly on
accordingly on 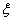 and, then summarising, we have the equation:
and, then summarising, we have the equation: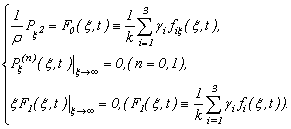
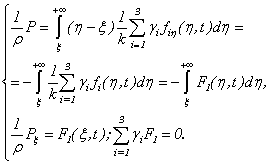
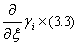 ], we have
], we have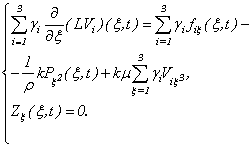 Then we have the following (3.4). Further, we have
Then we have the following (3.4). Further, we have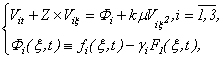
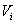 we have
we have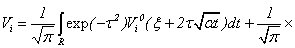
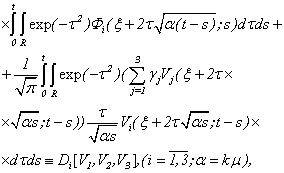
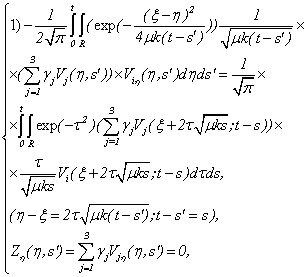 and
and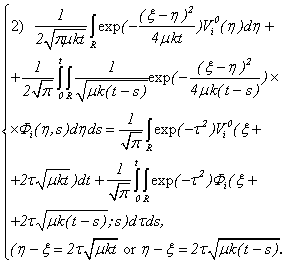 If functions
If functions 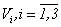 are system decisions (3.7) thus takes place (3.2) and
are system decisions (3.7) thus takes place (3.2) and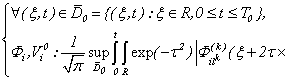
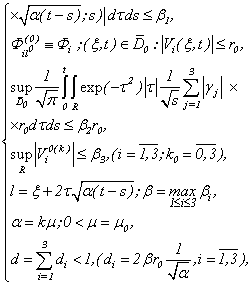
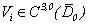 :
: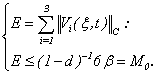
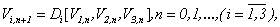
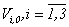 - initial estimates and at that
- initial estimates and at that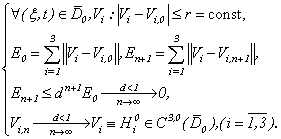
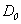 we name any continuous in
we name any continuous in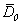 equation decision (3.7), when
equation decision (3.7), when 
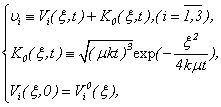
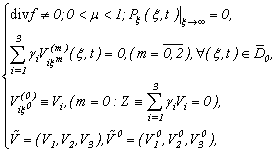
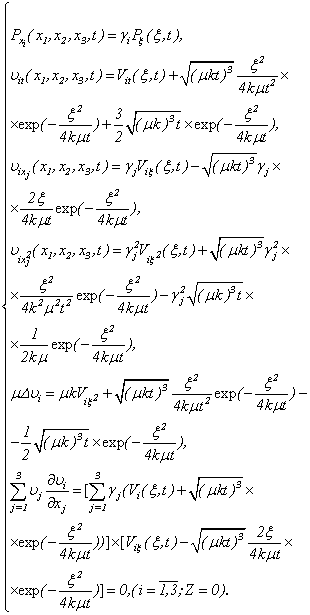 Then on the basis of functions
Then on the basis of functions 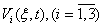 , system (1.1) it is equivalent will be transformed to a kind:
, system (1.1) it is equivalent will be transformed to a kind: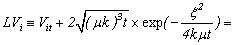
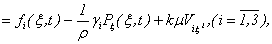
 Therefore
Therefore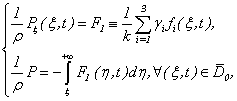
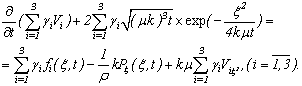 Theorem 4. Let functions are system decisions
Theorem 4. Let functions are system decisions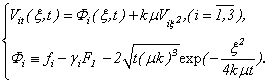
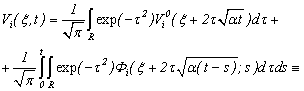
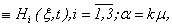
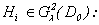
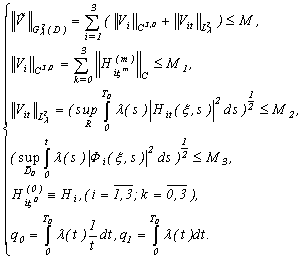 Theorem 5. If functions
Theorem 5. If functions 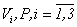 are system decisions (3.14), (3.15), (3.10) that (3.1) is the decision of system (1.1) in
are system decisions (3.14), (3.15), (3.10) that (3.1) is the decision of system (1.1) in  :
: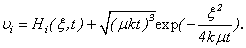
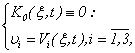
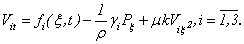
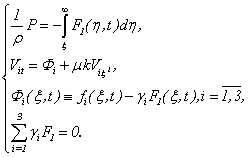
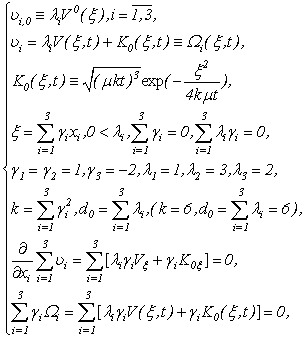 that
that 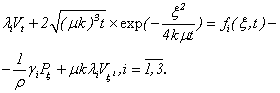
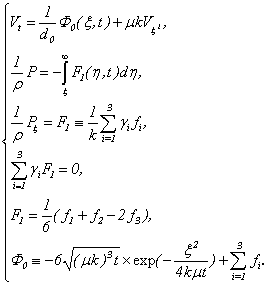 Then
Then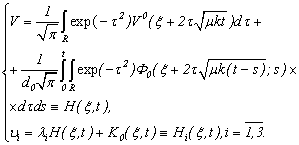 Remark 3. As
Remark 3. As 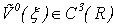 , that limitedly the decision of a problem of Navier-Stokes (1.1) - (1.3) with a condition (B) it is possible to prove limitation and in
, that limitedly the decision of a problem of Navier-Stokes (1.1) - (1.3) with a condition (B) it is possible to prove limitation and in 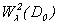 - weight space of type of Sobolev:
- weight space of type of Sobolev: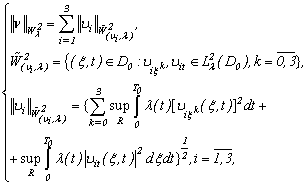 as
as 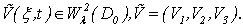
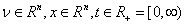 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML