1. Introduction

The development of geoinformation monitoring systems requires a solution of some problems concerning the organization of flows of measurement data. One of important problems here is making a statistical decision about the presence of one or other phenomenon on a surveyed part of the Earth surface. One of the features of information acquisition conditions for such a decision is that it is impossible to obtain large statistical samples. Therefore, there is a need in the development and research of optimal algorithms for making statistical decisions for small-size samples under information constraints.

When the number of observations is large enough, the problem is solved by the method of estimating the parameters of probability distributions, which is effective when the size of samples used for estimating the parameters indefinitely increases. Under a restricted size of samples, the decision making rule obtained by the method of estimating parameters does not satisfy the necessary optimality conditions, i.e., the constancy of the mean probability of error of the first kind and unbiasedness.

In the present work, we develop an adaptive learning algorithm for statistical decision making for exponential families of distributions under conditions of a priori parametric uncertainty for small sample sizes[1, 2].

2. Statement of the Problem

Very often, one encounters the following problem: under what class a measured random variable should be classified when a full probability description of these classes is unknown. The latter fact does not allow one to use classical results of the theory of statistical decision making. A decision can be obtained only by means of learning samples.

Let ξ, η, and ζ be independent random variables and f_ξ(x/ω₀), f_η(y/ω₁), and f_ζ(z/ω) be the distributions of probabilities ω₀, ω₁, ω € Ω. There are two alternatives for the parameter ω: H₀: ω = ω₀ and H₁: ω = ω₁.

Errors of the first kind are given by

α(φ, ω₀, x*, y*) = ∫ φ(x*, y*, z*)fω₀(z*)dz*

and

β(φ, ω₀, x*, y*) = ∫[1- φ(x*, y*, z*)]fω₁(z*)dz*.

The optimality conditions are

1. ά = α₀ (the constancy of errors of the first kind) and

2. 1 β > ά (unbiasedness).

In this work, we develop a mathematical apparatus and propose a generalized adaptive procedure for solving the problem of learning to distinguish between random variables from exponential families of distributions with unknown parameters for small-size samples under information constraints.

We show that available discrimination learning procedures in which first one estimates the parameters and then makes a choice between hypotheses do not satisfy the above requirements on optimal procedures.

When the number of observations is large enough, the problem is solved by the method for estimating the parameters of probability distributions, which is effective when the size of samples used for estimating the parameter indefinitely increases. When the sample size is limited, the decision making rule obtained by the method of estimating parameters does not satisfy the necessary optimality conditions: the constancy of the mean probability of error of the first kind and unbiasedness.

3. Statement of the Problem

The classical method of solving the problem is based on the sufficiently well developed theory of point estimates for unknown parameters of probability distributions. In the present problem, one obtains estimates for the parameters ω₀, ω₁, θ₁, and θ₀ from n₀ observations x* = (x₁, x₂,………..xn_o) and n₁ observations y* = (y₁, y₂,……….yn₁) of the random variables ξ and η, respectively.

Next, the method for constructing a decision rule is based on the Neyman--Pearson fundamental lemma: construct a likelihood relation

L(z*/θ₁,θ₀) = [f(z₁,z₂,…z_n/ θ₁)/ f(z₁,z₂,…z_n/ θ₀)] > C(θ₁,θ₀) and choose a threshold C(θ₁,θ₀).

1. θ₁ > θ₀ {s < t(n₀/n₁), s < n₀/G^-1_n(1 - α₀),

2. θ₁ < θ₀ { s > t(n₀/n₁) , s > n₀/G^-1_n( 1- α₀ ),

s = x/z, t = y/z,

G^-1_n = [1/(n-1)!] ∫ exp(-z) z^n-1 dz,

θ₁ and θ₀ are point estimates for ω₁ and ω₀.

The domains of making a hypothesis H₁ are shown in Fig. 1.

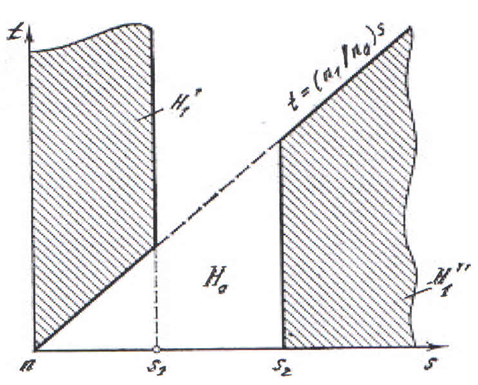Figure 1. Domains of making hypotheses for the classical decision rule

The graphs of probabilities for making a correct decision and errors of the first kind are shown in Fig. 2.

Figure 2 shows that the probability of error of the first kind is greater than the admissible value α₀ by a factor of two and a half.

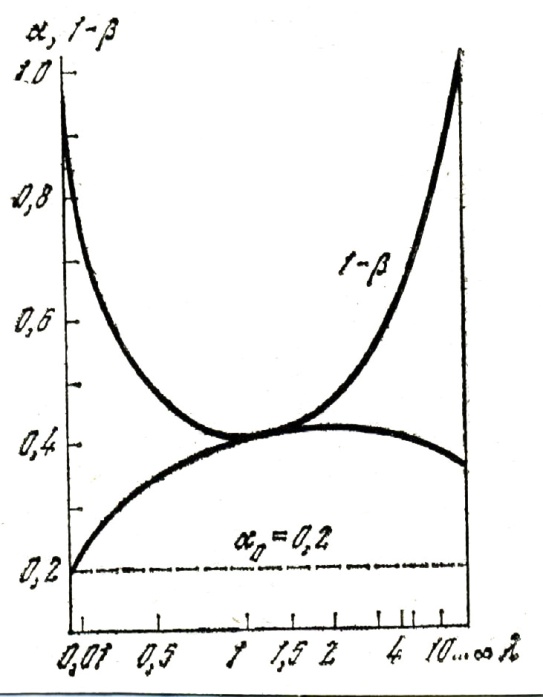Figure 2. Probabilities of making a correct decision and errors of the first kind

4. Decision Rule Satisfying Necessary Optimality Conditions

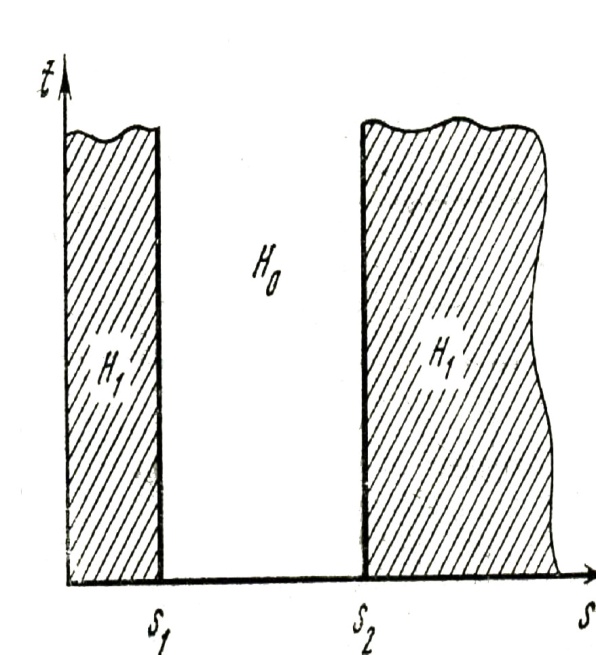Figure 3. Domains of making hypotheses for an optimal decision rule

An optimal decision rule in the class of decision rules shown in Fig. 3 is given by

{max α (s₁, s₂ / λ) = α₀ , max min D(s₁ ,s₂ / λ)

0<α<∞ (s₁,s₂) 0<λ<∞

D(s₁, s₂ / λ) = 1- β(s₁, s₂ / λ)

α(s₁, s₂ / λ) = P₀(s₁) + [P₀(∞) – P₀(s₁)]

D(s₁ ,s₂ / λ) = P₁(s₁) + [P₁(∞) – P₁(s₂)]

P_i(k) = ∫∫f_i(s,t)dsdt , where i = 0, 1.

Applying Lagrange's method of undetermined multipliers, we obtain the following set of equations for the optimal thresholds s₁ and s₂:

{ (s₁/s₂)n₀ = [(s₁ + 1)/(s₂ + 1)](n+n₀)

{ {1-∏ [(n₀ + j)/n!][[(n₀+n-1)(x₁+1)(n₀-1) – n]/(x₁+1)(n₀ +n-1)] –

{ -[[(n₀+n-1)(x₂+1)(n₀-1) – n]/(x₂+1)(n₀+n-1)]] – α₀ = 0.

The probabilities of making a correct solution and errors of the first kind are shown in Fig. 4.

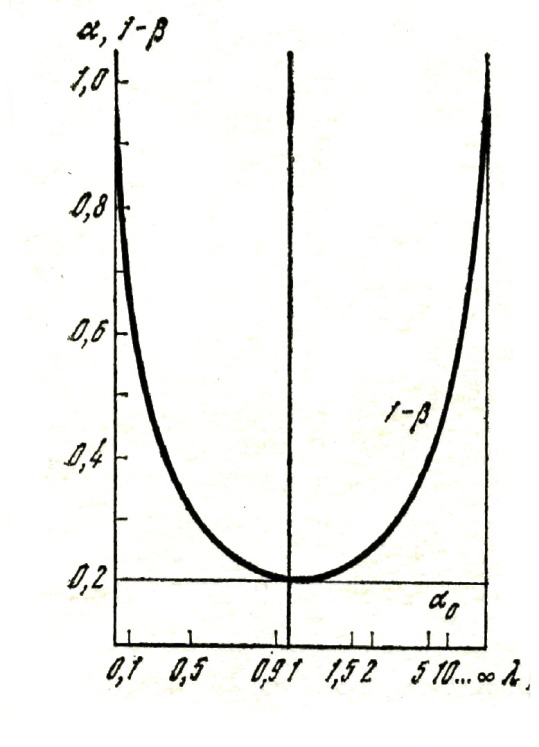Figure 4. Probabilities of making a correct solution and errors of the first kind

The procedure proposed satisfies the following necessary conditions: (1) the constancy of the mean probability of errors of the first kind α and (2) the unbiasedness condition 1-β < α.

The method described allows one to obtain decision rules for particular distributions from the exponential family of distributions.

5. Application

The analysis of statistical characteristics of "spottiness" was carried out for three types of areas of the Pacific ocean. These statistical characteristics were obtained for the most informative thresholds. The statistical characteristics of spottiness for the same areas were chosen on the basis of the criteria of minimal value of the correlation coefficient for a joint sample of positive and negative spots. The analysis of these characteristics shows that the statistical characteristics of spottiness for regions of moderate sea roughness and storm regions coincide. The correlation coefficient ρ_min attains its minimum in the case of most informative thresholds. However, for a quiet region, the situation is different[2].

Figure 5 illustrates the operation of the automated system in the mode of monitoring the surface temperature of Northern Atlantic based on data from «Kosmos-1151» (April 8-14, 1980) satellite. The system allows one to obtain temperature maps on a rather rarefied grid of satellite trajectories. The dots on the map denote areas where ship measurements were carried out. The analysis of satellite and contact measurements shows that the satellite data on the sea surface temperature are systematically understated compared with the ship measurement data, the difference being about 1.6 K on average.

The root-mean-square deviation of satellite data from the ship over the entire sample data is 3.3 K. The dotted lines on the map indicate areas where the difference between the ship and satellite measurements exceeds 4 K. It is remarkable that all these areas were characterized by high cloudiness (by weather forecast data). If we disregard these areas, then the root-mean-square deviation of the satellite measurements of temperature from the ship measurements amounts to 1.4.

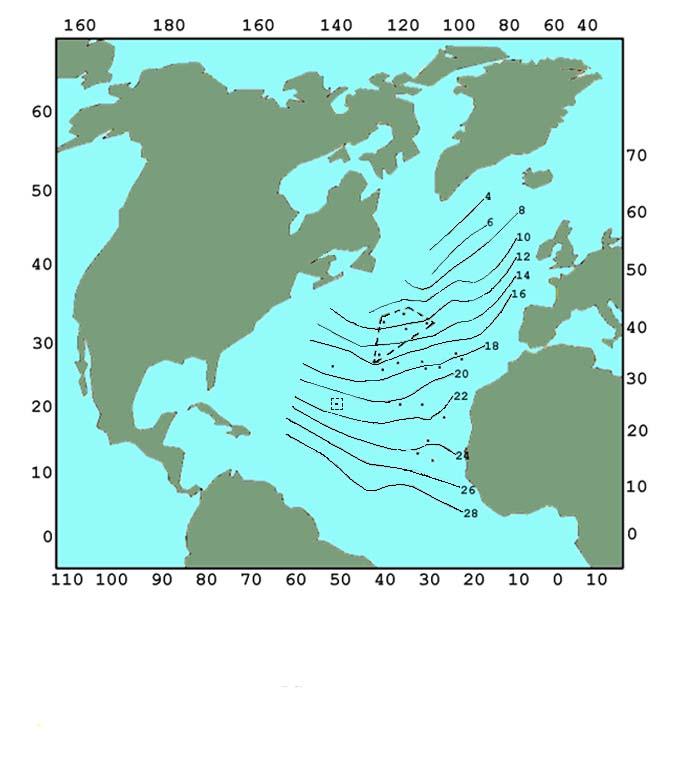Figure 5. Temperature map of Northern Atlantic

It follows from the aforesaid that the statistical characteristics of "spottiness" of microwave brightness temperature can be used to detect and classify various phenomena on the surface of the ocean that differ by the degree of sea roughness.

6. Conclusions

The analysis of empirical distributions of the spottiness of microwave brightness temperature has shown that, in most cases, the (l⁺, l-) characteristics are consistent with the exponential distribution, while the amplitude characteristics are consistent with the normal distribution. Therefore, to detect and classify phenomena on the surface of the ocean, one should apply optimal algorithms for the computer training to making statistical decisions for the aforesaid distributions.