Mohamed Tahir
Department of Mathematics, College of Sciences, University of Sharjah
Correspondence to: Mohamed Tahir, Department of Mathematics, College of Sciences, University of Sharjah.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The problem addressed is that of sequentially estimating θ, the shape parameter of the type I Pareto distribution, subject to the loss function  where c is a known cost per observation and
where c is a known cost per observation and  is the maximum likelihood estimator of θ. We propose a stopping time t and provide a second-order asymptotic expansion, as c → 0, for the regret incurred by the sequential procedure
is the maximum likelihood estimator of θ. We propose a stopping time t and provide a second-order asymptotic expansion, as c → 0, for the regret incurred by the sequential procedure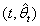 under the loss Lc. We also show that the point estimator
under the loss Lc. We also show that the point estimator 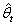 is asymptotically unbiased for θ.
is asymptotically unbiased for θ.
Keywords:
Anscombe’s Theorem, Doob’s Maximal Inequality, Excess over the Stopping Boundary, Hölder’s Inequality, Regret, Shape Parameter, Stopping Time, Uniform Integrability
Cite this paper: Mohamed Tahir, Sequential Estimation of the Shape Parameter of the Pareto Distribution, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 332-336. doi: 10.5923/j.ajms.20130306.05.
1. Introduction
The Type I Pareto distribution is a continuous distribution with probability density function (p.d.f.) 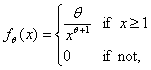 | (1) |
where θ is a positive number.The Pareto distribution was first formulated in the late 1800s by the Italian economist Vilfredo Pareto, who used this distribution to describe the allocation of wealth among individuals since it seemed to show rather well the way that a larger portion of the wealth of any society is owned by a smaller percentage of the people in that society. He also used it to describe the distribution of income. The Pareto distribution is not limited to describing wealth or income. It can be used as the distribution for insurance loss, oil reserve in a oil field, standardized price return on an individual stock, area burnt in a forest fire, etc…Let X1, , …, Xn denote independent observations to be taken sequentially up to a predetermined stage n from the Pareto distribution with p.d.f. (1). It is desired to estimate the parameter θ, subject to the loss function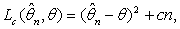 | (2) |
where c is a known cost per observation and  is the maximum likelihood estimator of θ. Since the log-likelihood function is
is the maximum likelihood estimator of θ. Since the log-likelihood function is  for observed values x1 > 1, …, xn > 1, of X1, , …, Xn, it follows that the maximum likelihood estimator of θ is
for observed values x1 > 1, …, xn > 1, of X1, , …, Xn, it follows that the maximum likelihood estimator of θ is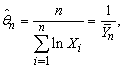 where
where 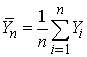 with Yi = lnXi, i = 1, …, n, and where the random variables Y1, …, Yn are independent with common distribution the Exponential distribution with mean
with Yi = lnXi, i = 1, …, n, and where the random variables Y1, …, Yn are independent with common distribution the Exponential distribution with mean 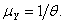 Expanding h(y) = 1/y about y = 1/θ and substituting
Expanding h(y) = 1/y about y = 1/θ and substituting 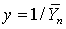 in the obtained expansion yields
in the obtained expansion yields 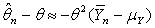 for large n. It follows that the risk incurred by estimating θ by
for large n. It follows that the risk incurred by estimating θ by 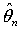 under the loss (2) is
under the loss (2) is for large n. The approximate risk is minimized with respect to n by choosing n as the greatest integer less than or equal to
for large n. The approximate risk is minimized with respect to n by choosing n as the greatest integer less than or equal to 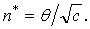 | (3) |
The minimum risk is  for sufficiently small c. Since n* depends on the unknown value of θ, there is no fixed-sample-size procedure that attains the minimum risk
for sufficiently small c. Since n* depends on the unknown value of θ, there is no fixed-sample-size procedure that attains the minimum risk 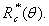 Therefore, we propose to use the sequential procedure
Therefore, we propose to use the sequential procedure 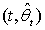 which stops the sampling process after observing Y1, …, Yt and estimates θ by
which stops the sampling process after observing Y1, …, Yt and estimates θ by  , where
, where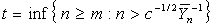 | (4) |
with m being a positive integer. The performance of the procedure 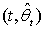 is measured by its regret, which is defined as
is measured by its regret, which is defined as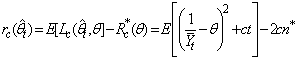 | (5) |
for c > 0.In this paper we propose a stopping time, t, based on (3), and provide a second-order asymptotic expansion, as c → 0, for the regret incurred by the sequential procedure under the loss (2). We also show that the estimator
under the loss (2). We also show that the estimator  is asymptotically unbiased for the shape parameter θ.The problem of sequentially estimating the mean of a population was studied by many authors. Starr and Woodroofe[7] considered the case in which X1, X2, … are i.i.d. Normal random variables and showed that the regret of his procedure is O(1). Then, Woodroofe[10] showed that the regret is 0.5 + o(1) if m ≥ 4. Martinsek[8] extended Woodroofe’s[10] result to the nonparametric case. For the distribution-free case, Ghosh and Mukhopadhyay[3] and Chow and Yu[5] established asymptotic risk efficiency under certain conditions. Tahir[9] proposed a class of bias-reduction estimators of the mean of the one-parameter exponential family and provided an asymptotic second-order lower bound for the regret.
is asymptotically unbiased for the shape parameter θ.The problem of sequentially estimating the mean of a population was studied by many authors. Starr and Woodroofe[7] considered the case in which X1, X2, … are i.i.d. Normal random variables and showed that the regret of his procedure is O(1). Then, Woodroofe[10] showed that the regret is 0.5 + o(1) if m ≥ 4. Martinsek[8] extended Woodroofe’s[10] result to the nonparametric case. For the distribution-free case, Ghosh and Mukhopadhyay[3] and Chow and Yu[5] established asymptotic risk efficiency under certain conditions. Tahir[9] proposed a class of bias-reduction estimators of the mean of the one-parameter exponential family and provided an asymptotic second-order lower bound for the regret.
2. Asymptotic Expansion for the Regret of the Sequential Procedure 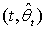
Theorem 1: Let t be as in (4) with m ≥ 1, then  as c → 0.Proof: The stopping time t can be rewritten as
as c → 0.Proof: The stopping time t can be rewritten as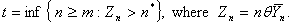 | (6) |
Furthermore, let 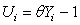 for i = 1, 2, … and let
for i = 1, 2, … and let  Then,
Then,  with g(u) = u + 1. Since g is a convex function and
with g(u) = u + 1. Since g is a convex function and 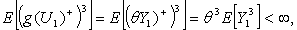 where U += max {U, 0}, it follows from Proposition 5 and Theorem 1 of[2] that
where U += max {U, 0}, it follows from Proposition 5 and Theorem 1 of[2] that  as c → 0, where ρ denotes the asymptotic mean of the excess over the stopping boundary, Bc = tZt – n*. Moreover,
as c → 0, where ρ denotes the asymptotic mean of the excess over the stopping boundary, Bc = tZt – n*. Moreover, where
where 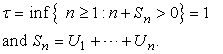 The theorem follows.Expanding h(y) = 1/y about
The theorem follows.Expanding h(y) = 1/y about  and substituting
and substituting  in the obtained expansion yields
in the obtained expansion yields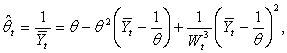 | (7) |
where Wt is a random variable lying between 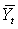 and
and 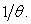 Lemma 1: Let t be as in (4) and let p > 1. Then, (i)
Lemma 1: Let t be as in (4) and let p > 1. Then, (i) 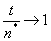 w.p.1 as c → 0.(ii)
w.p.1 as c → 0.(ii) 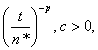 is uniformly integrable;(iii)
is uniformly integrable;(iii) 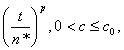 is uniformly integrable if m > p.Proof. Assertion (i) holds by Proposition 2 of Aras and Woodroofe[2]. For the second assertion,
is uniformly integrable if m > p.Proof. Assertion (i) holds by Proposition 2 of Aras and Woodroofe[2]. For the second assertion, 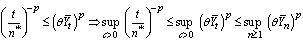 since
since 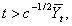 by the definition of t. Thus, Assertion (ii) holds since
by the definition of t. Thus, Assertion (ii) holds since By Doob’s maximal inequality (see[4]). To establish (iii), observe that
By Doob’s maximal inequality (see[4]). To establish (iii), observe that  on {t > m}, by the definition of t; so that
on {t > m}, by the definition of t; so that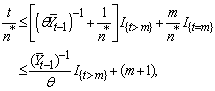 where I{.} denotes the indicator function. This implies that
where I{.} denotes the indicator function. This implies that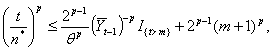 by the cr-inequality (see Loève[6]). Since
by the cr-inequality (see Loève[6]). Since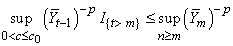 and
and 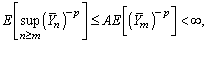 for some A >0, by Doob’s maximal inequality, Assertion (ii) follows.Lemma 2: Let p > 1. If m > p, then,(i)
for some A >0, by Doob’s maximal inequality, Assertion (ii) follows.Lemma 2: Let p > 1. If m > p, then,(i) 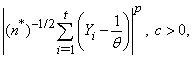 is uniformly integrable and(ii)
is uniformly integrable and(ii) 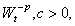 is uniformly integrable.Proof. The first assertion follows by using Assertion (i) of Lemma 1 and Theorem 2 of[3]. The second assertion follows since
is uniformly integrable.Proof. The first assertion follows by using Assertion (i) of Lemma 1 and Theorem 2 of[3]. The second assertion follows since 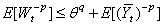 and
and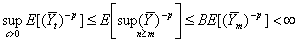 for some constant B > 0, by Doob’s maximal inequality.Theorem 2: Let
for some constant B > 0, by Doob’s maximal inequality.Theorem 2: Let  be as in (5). Then,
be as in (5). Then,  as c → 0.Proof. It follows from (5) that
as c → 0.Proof. It follows from (5) that 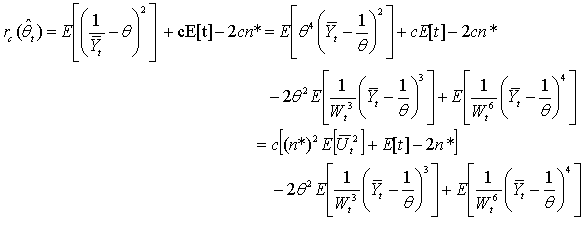 | (8) |
for c > 0. Next, by Corollary 1 of Aras and Woodroofe[2],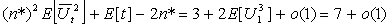 | (9) |
as c → 0. Now, let 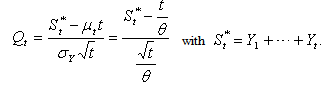 | (10) |
and let Z denote a random variable having the Standard Normal distribution. Then, 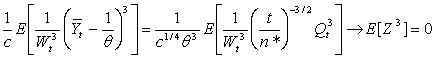
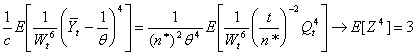 | (11) |
as c → 0, by Assertion (i) of Lemma 1, the fact that Qt → Z in distribution as c → 0 by Anscombe’s theorem (see[1]) and the fact that Wt → 1/θ w.p.1 as c → 0. The uniform integrability of 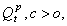 follows from Assertions (ii) of Lemmas 1 and 2 since
follows from Assertions (ii) of Lemmas 1 and 2 since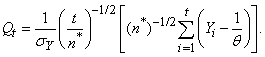 Now take the limit as c → 0 in (8) and use (9) and (11) to complete the proof of the theorem.Lemma 3: Let t be defined by (4). If m > 4, then
Now take the limit as c → 0 in (8) and use (9) and (11) to complete the proof of the theorem.Lemma 3: Let t be defined by (4). If m > 4, then 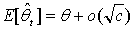 as c → 0.Proof: It follows from (7) that
as c → 0.Proof: It follows from (7) that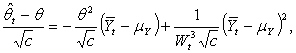 | (12) |
where Wt is a random variable lying between 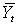 and µY =
and µY =  Next,
Next,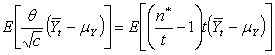 | (13) |
by (3) and Wald’s lemma. Moreover, it follows from (6) that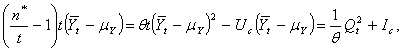 say, where
say, where 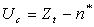 denotes the excess over the stopping boundary and Qt is as in (10). Now,
denotes the excess over the stopping boundary and Qt is as in (10). Now, 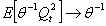 as c → 0, by Anscombe’s theorem and the fact that
as c → 0, by Anscombe’s theorem and the fact that 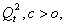 is uniformly integrable. Also, by Hölder’s inequality,
is uniformly integrable. Also, by Hölder’s inequality,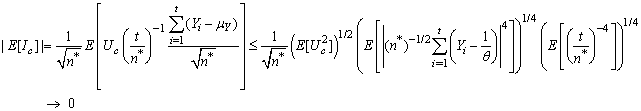 as c → 0, by Proposition 7 of[2] and Lemmas 1 and 2.Using these results in (13) yields
as c → 0, by Proposition 7 of[2] and Lemmas 1 and 2.Using these results in (13) yields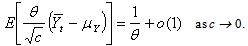 | (14) |
For the second term in (12), observe that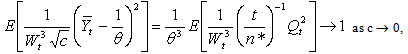 | (15) |
by the fact that Wt → 1/θ w.p.1 as c → 0, Assertions (i) and (ii) of Lemma 1, Anscombe’s theorem and the uniform integrability of  . The lemma follows by using (14) and (15) in (12).
. The lemma follows by using (14) and (15) in (12).
3. Conclusions
1- We have proposed a sequential procedure for estimating the shape parameter of the type I Pareto distribution and provided a second-order asymptotic expansion for the regret. The procedure can be used for the data representing the losses for insurance policyholders or the insured values of homes. It specifies how many policyholders or homes should be selected and provides an estimate of θ based on this number.2- Since the asymptotic regret is positive for small values of the cost of sampling, it would be interesting to find a sequential procedure whose asymptotic regret is negative.
References
| [1] | Anscombe, F., 1952, Large sample theory of sequential estimation, Proeedings Cambridge Philos. Soc., 48, 600-607. |
| [2] | Aras, G. and Woodroofe, M., 1993, Asymptotic expansions for the moments of a randomly stopped average, Annals of Statistics, 21, 503-519. |
| [3] | Chow, Y. S., Hsiung, C. A., and Lai, T. L., 1979, Extended renewal theory and Moment convergence in Anscombe’s theorem, the Annals of Probability, 7, 304-318. |
| [4] | Doob, J.L., 1953, Stochastic Processes, Wiley, New York |
| [5] | Ghosh, M. and Mukhopadhyay, N.,1979, Sequential point estimation of the mean when the distribution is unspecified, Commun. Statist.-Theory & Methods, A8, 637-652. |
| [6] | Loève, M., 1977, Probability Theory, 4th Ed., Springer-Verlag, New York. |
| [7] | Starr, N. and Woodroofe, M., 1969, Remarks on sequential point estimation, Proc. Nat. Acad. Sci., U.S.A., 63, 285-288. |
| [8] | Martinsek, A.T., 1983, Second order approximation to the risk of a sequential Procedure, Annals of Statistics, 11, 827-836. |
| [9] | Tahir, M., 1989, An asymptotic lower bound for the local minimax regret in sequential point estimation, Annals of Statistics, 17, 1335-1346 |
| [10] | Woodroofe, M., 1977, Second order approximations for sequential point and interval estimation, Annals of Statistics, 5, 984-995. |

 where c is a known cost per observation and
where c is a known cost per observation and  is the maximum likelihood estimator of θ. We propose a stopping time t and provide a second-order asymptotic expansion, as c → 0, for the regret incurred by the sequential procedure
is the maximum likelihood estimator of θ. We propose a stopping time t and provide a second-order asymptotic expansion, as c → 0, for the regret incurred by the sequential procedure under the loss Lc. We also show that the point estimator
under the loss Lc. We also show that the point estimator 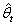 is asymptotically unbiased for θ.
is asymptotically unbiased for θ.
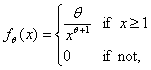
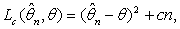
 is the maximum likelihood estimator of θ. Since the log-likelihood function is
is the maximum likelihood estimator of θ. Since the log-likelihood function is  for observed values x1 > 1, …, xn > 1, of X1, , …, Xn, it follows that the maximum likelihood estimator of θ is
for observed values x1 > 1, …, xn > 1, of X1, , …, Xn, it follows that the maximum likelihood estimator of θ is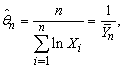 where
where 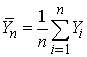 with Yi = lnXi, i = 1, …, n, and where the random variables Y1, …, Yn are independent with common distribution the Exponential distribution with mean
with Yi = lnXi, i = 1, …, n, and where the random variables Y1, …, Yn are independent with common distribution the Exponential distribution with mean 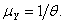 Expanding h(y) = 1/y about y = 1/θ and substituting
Expanding h(y) = 1/y about y = 1/θ and substituting 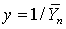 in the obtained expansion yields
in the obtained expansion yields 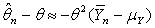 for large n. It follows that the risk incurred by estimating θ by
for large n. It follows that the risk incurred by estimating θ by 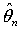 under the loss (2) is
under the loss (2) is for large n. The approximate risk is minimized with respect to n by choosing n as the greatest integer less than or equal to
for large n. The approximate risk is minimized with respect to n by choosing n as the greatest integer less than or equal to 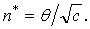
 for sufficiently small c. Since n* depends on the unknown value of θ, there is no fixed-sample-size procedure that attains the minimum risk
for sufficiently small c. Since n* depends on the unknown value of θ, there is no fixed-sample-size procedure that attains the minimum risk 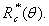 Therefore, we propose to use the sequential procedure
Therefore, we propose to use the sequential procedure 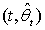 which stops the sampling process after observing Y1, …, Yt and estimates θ by
which stops the sampling process after observing Y1, …, Yt and estimates θ by  , where
, where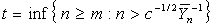
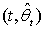 is measured by its regret, which is defined as
is measured by its regret, which is defined as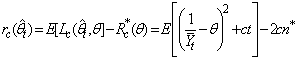
 under the loss (2). We also show that the estimator
under the loss (2). We also show that the estimator  is asymptotically unbiased for the shape parameter θ.The problem of sequentially estimating the mean of a population was studied by many authors. Starr and Woodroofe[7] considered the case in which X1, X2, … are i.i.d. Normal random variables and showed that the regret of his procedure is O(1). Then, Woodroofe[10] showed that the regret is 0.5 + o(1) if m ≥ 4. Martinsek[8] extended Woodroofe’s[10] result to the nonparametric case. For the distribution-free case, Ghosh and Mukhopadhyay[3] and Chow and Yu[5] established asymptotic risk efficiency under certain conditions. Tahir[9] proposed a class of bias-reduction estimators of the mean of the one-parameter exponential family and provided an asymptotic second-order lower bound for the regret.
is asymptotically unbiased for the shape parameter θ.The problem of sequentially estimating the mean of a population was studied by many authors. Starr and Woodroofe[7] considered the case in which X1, X2, … are i.i.d. Normal random variables and showed that the regret of his procedure is O(1). Then, Woodroofe[10] showed that the regret is 0.5 + o(1) if m ≥ 4. Martinsek[8] extended Woodroofe’s[10] result to the nonparametric case. For the distribution-free case, Ghosh and Mukhopadhyay[3] and Chow and Yu[5] established asymptotic risk efficiency under certain conditions. Tahir[9] proposed a class of bias-reduction estimators of the mean of the one-parameter exponential family and provided an asymptotic second-order lower bound for the regret. 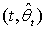
 as c → 0.Proof: The stopping time t can be rewritten as
as c → 0.Proof: The stopping time t can be rewritten as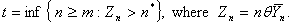
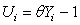 for i = 1, 2, … and let
for i = 1, 2, … and let  Then,
Then,  with g(u) = u + 1. Since g is a convex function and
with g(u) = u + 1. Since g is a convex function and 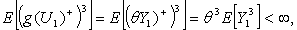 where U += max {U, 0}, it follows from Proposition 5 and Theorem 1 of[2] that
where U += max {U, 0}, it follows from Proposition 5 and Theorem 1 of[2] that  as c → 0, where ρ denotes the asymptotic mean of the excess over the stopping boundary, Bc = tZt – n*. Moreover,
as c → 0, where ρ denotes the asymptotic mean of the excess over the stopping boundary, Bc = tZt – n*. Moreover, where
where 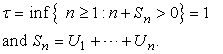 The theorem follows.Expanding h(y) = 1/y about
The theorem follows.Expanding h(y) = 1/y about  and substituting
and substituting  in the obtained expansion yields
in the obtained expansion yields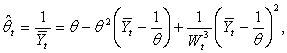
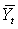 and
and 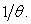 Lemma 1: Let t be as in (4) and let p > 1. Then, (i)
Lemma 1: Let t be as in (4) and let p > 1. Then, (i) 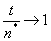 w.p.1 as c → 0.(ii)
w.p.1 as c → 0.(ii) 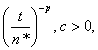 is uniformly integrable;(iii)
is uniformly integrable;(iii) 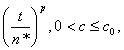 is uniformly integrable if m > p.Proof. Assertion (i) holds by Proposition 2 of Aras and Woodroofe[2]. For the second assertion,
is uniformly integrable if m > p.Proof. Assertion (i) holds by Proposition 2 of Aras and Woodroofe[2]. For the second assertion, 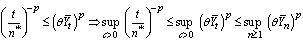 since
since 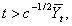 by the definition of t. Thus, Assertion (ii) holds since
by the definition of t. Thus, Assertion (ii) holds since By Doob’s maximal inequality (see[4]). To establish (iii), observe that
By Doob’s maximal inequality (see[4]). To establish (iii), observe that  on {t > m}, by the definition of t; so that
on {t > m}, by the definition of t; so that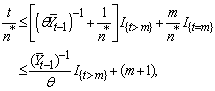 where I{.} denotes the indicator function. This implies that
where I{.} denotes the indicator function. This implies that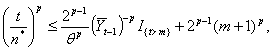 by the cr-inequality (see Loève[6]). Since
by the cr-inequality (see Loève[6]). Since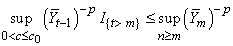 and
and 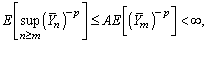 for some A >0, by Doob’s maximal inequality, Assertion (ii) follows.Lemma 2: Let p > 1. If m > p, then,(i)
for some A >0, by Doob’s maximal inequality, Assertion (ii) follows.Lemma 2: Let p > 1. If m > p, then,(i) 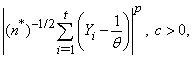 is uniformly integrable and(ii)
is uniformly integrable and(ii) 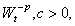 is uniformly integrable.Proof. The first assertion follows by using Assertion (i) of Lemma 1 and Theorem 2 of[3]. The second assertion follows since
is uniformly integrable.Proof. The first assertion follows by using Assertion (i) of Lemma 1 and Theorem 2 of[3]. The second assertion follows since 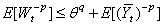 and
and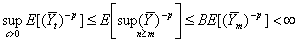 for some constant B > 0, by Doob’s maximal inequality.Theorem 2: Let
for some constant B > 0, by Doob’s maximal inequality.Theorem 2: Let  be as in (5). Then,
be as in (5). Then,  as c → 0.Proof. It follows from (5) that
as c → 0.Proof. It follows from (5) that 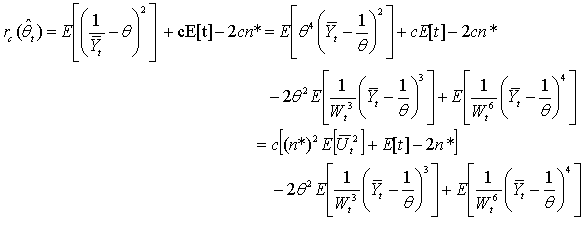
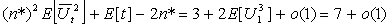
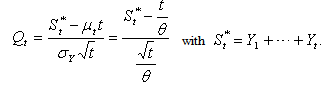
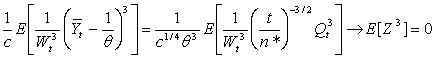
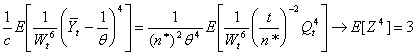
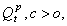 follows from Assertions (ii) of Lemmas 1 and 2 since
follows from Assertions (ii) of Lemmas 1 and 2 since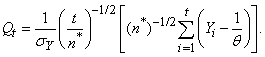 Now take the limit as c → 0 in (8) and use (9) and (11) to complete the proof of the theorem.Lemma 3: Let t be defined by (4). If m > 4, then
Now take the limit as c → 0 in (8) and use (9) and (11) to complete the proof of the theorem.Lemma 3: Let t be defined by (4). If m > 4, then 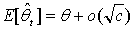 as c → 0.Proof: It follows from (7) that
as c → 0.Proof: It follows from (7) that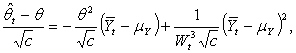
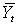 and µY =
and µY =  Next,
Next,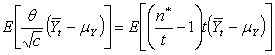
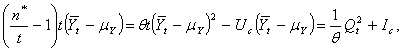 say, where
say, where 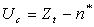 denotes the excess over the stopping boundary and Qt is as in (10). Now,
denotes the excess over the stopping boundary and Qt is as in (10). Now, 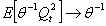 as c → 0, by Anscombe’s theorem and the fact that
as c → 0, by Anscombe’s theorem and the fact that 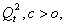 is uniformly integrable. Also, by Hölder’s inequality,
is uniformly integrable. Also, by Hölder’s inequality,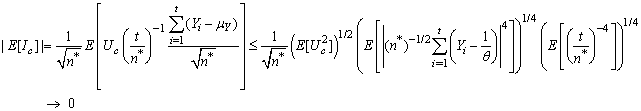 as c → 0, by Proposition 7 of[2] and Lemmas 1 and 2.Using these results in (13) yields
as c → 0, by Proposition 7 of[2] and Lemmas 1 and 2.Using these results in (13) yields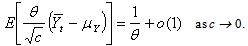
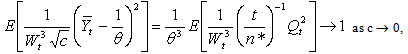
 . The lemma follows by using (14) and (15) in (12).
. The lemma follows by using (14) and (15) in (12). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML