-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(6): 312-314
doi:10.5923/j.ajms.20130306.03
Goal Programming Model for Personnel Management in Tea Industry: A Case Study of Barak Valley of Assam (India)
Nabendu Sen
Department of Mathematics, Assam University, Silchar, Pin-788011, India
Correspondence to: Nabendu Sen, Department of Mathematics, Assam University, Silchar, Pin-788011, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The much anticipated productivity and better performance of tea-industry counts on the proper utilization of human resources. Tea industry in Barak valley of Assam (India) involves different types of employees in field and factory. Moreover the overall management is monitored by administrative staffs. In this paper a model is developed so that payroll cost per month is minimized and at the same time the production target is also achieved. The study is based on the information from a leading tea industry of this valley engaged in producing C.T.C. tea of different varieties.
Keywords: Goal Programming, Personnel Management
Cite this paper: Nabendu Sen, Goal Programming Model for Personnel Management in Tea Industry: A Case Study of Barak Valley of Assam (India), American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 312-314. doi: 10.5923/j.ajms.20130306.03.
Article Outline
1. Introduction
- Goal Programming is one of the most developed optimization techniques inevitable for making strategies and schedules of conflicting nature and of different dimensions which is necessary for decision-making in Industrial sectors. A good number of researchers have already formulated models successfully for different agro-based industries with lucrative outcome for management. Researchers have also developed analytical models for shift-by-shift allocation decisions for final assignment of nurses and non-professional personnel to hospital units. Warner[1], Warner and Prawda[2] studied in this regard. Wolfe and Young[3,4] developed a model for determining nurse staffing in a hospital unit. Trivedi[5] proposed a mixed integer goal programming model for nursing service budgeting by taking into account part-time, full time and overtime nurses on week days as well as weekends. Pal and Sen[6] used goal programming procedures for proper allocation of teaching personnel to teaching departments of academic activity of a university. We find more literature of human resources allocation in[7,8,9,10]. Till date no effort has been given to study human resource allocation in tea industry. Tea industry of Barak Valley bears a large number of employees of different but mainly of 13 grades. The involvement of employees in factory, field and administration makes an important factor for management. Even one can also find workers who work on for daily basis. The management of tea industry is always willing to utilize all type of the employees for optimal returns in terms of production and profit.Our study is concerned with that in tea industry where Management seeks to minimize the total payroll costs, while maximizing human resources utilization.The different constraints are given on the basis of information available from tea industries. The goals of the developed model are also given priorities according to the management point of view.
2. GP Model Development
2.1. System Constraints
- (i) Budget allocation for the salary of staffs:In the process, the management already had set their budget for the whole process. So the total amount available for payroll is limited per month which can be stated as
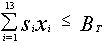 (ii) Total number of workers in the process:The at most number of total individuals that can be afforded by the management in specified budgeted salary can be stated as
(ii) Total number of workers in the process:The at most number of total individuals that can be afforded by the management in specified budgeted salary can be stated as 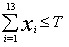
2.2. Goal Constraints
- The LGP model constraints with deviational variables are formulated as follows:P1: Minimum payroll goal (Priority 1)To achieve the minimum payroll cost for budget planned, the management wishes not to spend more than allotted budget. The constraints willing to minimize the overachievement can be stated as,
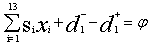 P2: Utilization of factory staffs (Priority 2)Achievement of the proper utilization of factory staffs is to be considered. Lesser number of workers is desired but more staffs can also be hired and used in case of higher demand, so both underachievement and overachievement will come into consideration and it can be expressed as,
P2: Utilization of factory staffs (Priority 2)Achievement of the proper utilization of factory staffs is to be considered. Lesser number of workers is desired but more staffs can also be hired and used in case of higher demand, so both underachievement and overachievement will come into consideration and it can be expressed as,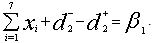 P3: Budget for the daily wages for labour in factory (Priority 3)As these workers of factory are not taken in permanent basis, so the budget allocation for this particular case is to be considered separately and desired to be minimized and it can be expressed as,
P3: Budget for the daily wages for labour in factory (Priority 3)As these workers of factory are not taken in permanent basis, so the budget allocation for this particular case is to be considered separately and desired to be minimized and it can be expressed as,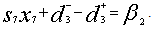 P4: Attain a reduced overtime (Priority 4)When the demand in market is higher, overtime is allowed in the factory but it is desirable to get it minimized from management point of view to control their allotted budget, the constraint can be expressed as
P4: Attain a reduced overtime (Priority 4)When the demand in market is higher, overtime is allowed in the factory but it is desirable to get it minimized from management point of view to control their allotted budget, the constraint can be expressed as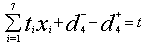 P5: Number of workers in field (Priority 5)It is desired to have lesser number of workers in the field and so the goal constraint to restrict the overachievement of workers in field which can be expressed as,
P5: Number of workers in field (Priority 5)It is desired to have lesser number of workers in the field and so the goal constraint to restrict the overachievement of workers in field which can be expressed as,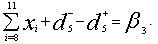 P6: Number of administrative staffs (Priority 6)It is desired to have lesser number of employees in the administration and the constraint to minimize the overachievement can be expressed as,
P6: Number of administrative staffs (Priority 6)It is desired to have lesser number of employees in the administration and the constraint to minimize the overachievement can be expressed as,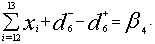 P7: Budget for the factory staffs (Priority 7)To achieve the minimum budget for the factory staffs, the goal constraint to minimize the positive deviation from the goal may be stated as,
P7: Budget for the factory staffs (Priority 7)To achieve the minimum budget for the factory staffs, the goal constraint to minimize the positive deviation from the goal may be stated as,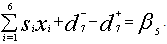 P8: Budget for the field staffs (Priority 8)The desire is to achieve the minimum budget for the field staffs. The goal constraint to minimize positive deviation may be stated as,
P8: Budget for the field staffs (Priority 8)The desire is to achieve the minimum budget for the field staffs. The goal constraint to minimize positive deviation may be stated as,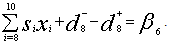 P9: Budget for the administration staffs (Priority 9)Achievement of the minimum budget for the administrations staffs is desired. The goal constraint is to minimize positive deviation from goal may be stated as,
P9: Budget for the administration staffs (Priority 9)Achievement of the minimum budget for the administrations staffs is desired. The goal constraint is to minimize positive deviation from goal may be stated as,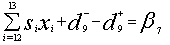 P10: Budget for the crèche (Priority 10)These workers of field are to look after the children of puckers, they are not regular basis workers and so the budget allocation case for them is considered separately by management and as well another desired constraint to minimize the overachievement can be expressed as,
P10: Budget for the crèche (Priority 10)These workers of field are to look after the children of puckers, they are not regular basis workers and so the budget allocation case for them is considered separately by management and as well another desired constraint to minimize the overachievement can be expressed as,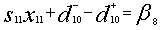 Achievement function is
Achievement function is 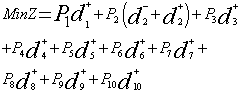
3. Solution Procedure for the Developed Model
- The developed GP model can be validated with the data available from respective tea industries. Uses of software like LING, Micro-management Software etc will be of immense help.ConclusionThe G.P. model has been developed to help in decision-making in a tea-industry personnel management. G.P is applied with a computer program to find the satisfactory solution of personnel management problem. As the variables in this model are number of employees in different jobs, so the study of integer behavior will be meaningful in the proposed model and hence the need for study of Integer GP comes forward. The study will be better if we rearrange the ranking of priority from author’s point of view. Moreover the introduction of other constraints (goal as well as structural) in the present model with the change of time, will also improve it for better solution. The model can further be improved in future with inclusion of new variables depending on the seniority of employees .A comparative study can be done by using different optimization techniques available in literature to solve this problem and to have a justification which optimization technique is most suitable for decision-making problems. Our study can be applied to other industries having the similar constraints especially where time and resources are limited.Symbols and Variables
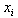 = The number of workers in i-th type of work(ie variables are taken corresponding to Factory In charge, Head tea house staff,Electrician,Fitter,Turner,Excise clerk, Daily wages labour, Field Asst., Field staff, Substaff, Crech, Manager,Deputy Manager respectively).(i=1,2,3,…….13)
= The number of workers in i-th type of work(ie variables are taken corresponding to Factory In charge, Head tea house staff,Electrician,Fitter,Turner,Excise clerk, Daily wages labour, Field Asst., Field staff, Substaff, Crech, Manager,Deputy Manager respectively).(i=1,2,3,…….13)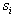 = Salary of each worker in i-th type of work.
= Salary of each worker in i-th type of work.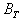 = The total budget allotted for the salary of all workers.T = The total number of workers in the system.
= The total budget allotted for the salary of all workers.T = The total number of workers in the system.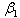 = The desired number of workers in factory.
= The desired number of workers in factory.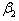 = The desired budget for the daily wages labour in factory.
= The desired budget for the daily wages labour in factory.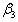 = The desired time to be utilized in factory.
= The desired time to be utilized in factory.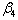 =The desired number of administrative staffs.
=The desired number of administrative staffs.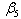 = The desired budget for the factory staffs.
= The desired budget for the factory staffs.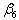 = The desired budget for the field staffs.
= The desired budget for the field staffs.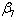 =The desired budget for the administration staffs.
=The desired budget for the administration staffs.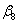 =The desired budget for the crèche
=The desired budget for the crèche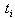 = The over time used by each workers in factory.
= The over time used by each workers in factory.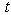 =The desired time allowed by management for overtime.
=The desired time allowed by management for overtime.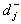 =The negative deviation from j-th goal.
=The negative deviation from j-th goal.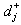 =The positive deviation from j-th goal.
=The positive deviation from j-th goal.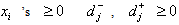 and
and 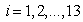 ,
, 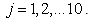
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML