Purnachandra Rao Koya, Ayele Taye Goshu
School of Mathematical and Statistical Sciences, Hawassa University
Correspondence to: Ayele Taye Goshu, .
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we consider the commonly used growth models and explicitly shown that each is a solution of the rate-state ordinary differential equation 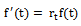 which describes biological growths.We construct growth function
which describes biological growths.We construct growth function 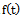 and relative growth function
and relative growth function 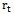 for the models: Generalized logistic, Particular case of generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians working in the fields of Biological sciences and non-availability of these derivations in literature.
for the models: Generalized logistic, Particular case of generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians working in the fields of Biological sciences and non-availability of these derivations in literature.
Keywords:
Growth Models, Rate-State Equation, Gompertz, Logistic, Richards, Weibull
Cite this paper: Purnachandra Rao Koya, Ayele Taye Goshu, Solutions of Rate-state Equation Describing Biological Growths, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 305-311. doi: 10.5923/j.ajms.20130306.02.
1. Introduction
Measuring biological growth has been important in many fields. Many researchers have contributed in developing relevant models: Brody[1] for Brody function; Bertalanffy[2] for Von Bertalanffy function, Richards[3], France & Thornley[4] for Richards function; Winsor[5] for Gompertz function; Nelder[6], Brown et al[7], Robertson[8] for Logistic function; Eberhardt & Breiwick[9], Fekedulegn et al[10], Ayala et al[11] and Nelder[6] for Generalized Logistic, Rawlings & Cure[12] and Rawlings et al[13] for Weibull function; Spillman & Lang[14] and Brody[1] for Monomolecular function.The growth models have been widely used in many biological growth problems including: in animal sciences (France et al[15]; Brown et al[7]; Brody[1]; Robertson[8]; Winsor[5]; Ersoy et al[16]) and in forestry (Lie and Zhang[17]; Zeide[18]).The generalized logistic function has been studied by some researchers (Eberhardt and Breiwick[9]; Fekedulegn et al[10]; Ayala et al[11]; Nelder,[6]). Eberhardt and Breiwick[9] applied the models to growth of birds and mammal populations.The mathematical representation of the relative growth is described by the ordinary differential equation (ODE) or rate-state equation: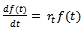 | (1) |
where 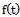 is representing growth function and
is representing growth function and 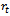 is relative rate function at time
is relative rate function at time 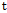 . This ordinary differential equation has many solutions among which some are studied here. The purpose of this paper is to explicitly show that the commonly used growth models are solutions of the rate-state equation by constructing
. This ordinary differential equation has many solutions among which some are studied here. The purpose of this paper is to explicitly show that the commonly used growth models are solutions of the rate-state equation by constructing 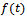 and
and 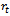 .In the current paper, detailed derivations of
.In the current paper, detailed derivations of 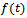 and
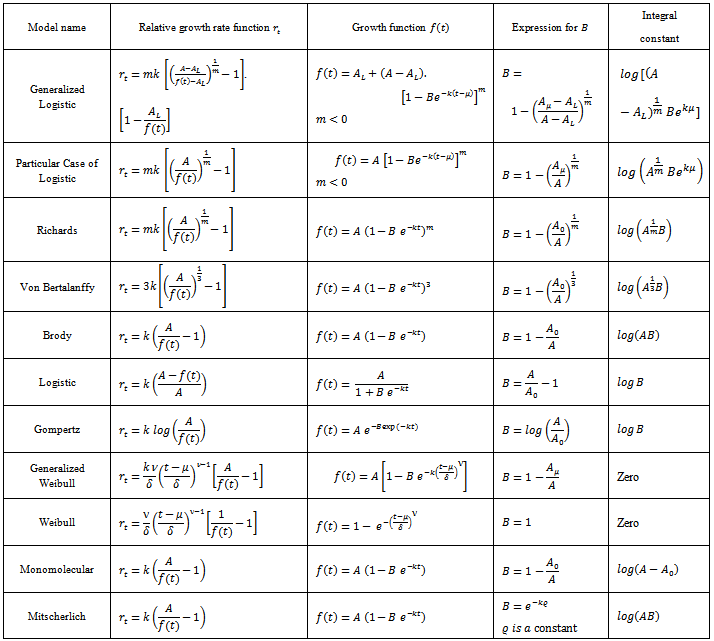
and 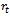 are presented considering non mathematicians working in the fields of Biological sciences and non availability of these derivations in the literature. All the growth functions discussed here are displayed in Table 1 together with respective relative growth rate functions, expression for
are presented considering non mathematicians working in the fields of Biological sciences and non availability of these derivations in the literature. All the growth functions discussed here are displayed in Table 1 together with respective relative growth rate functions, expression for 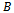 and integral constant.
and integral constant.
2. Derivations of Growth and Relative Growth Rate Functions
In this section we consider various growth functions and construct for them the respective 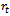 and
and 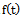 . The growth curves considered in this paper are: Generalized logistic, Particular case of the generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich functions.
. The growth curves considered in this paper are: Generalized logistic, Particular case of the generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich functions.
2.1. Generalized Logistic Function
The Generalized Logistic function as given in (Wikipedia) is expressed in its original notations as 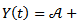
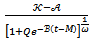 which we now re-express in the same notations used in this paper as
which we now re-express in the same notations used in this paper as 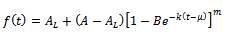 | (2) |
by replacing in the equation 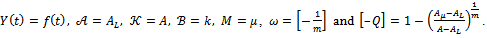 Detailed derivations of
Detailed derivations of 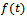 and
and 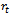 for generalized logistic function are given here under.Derivation of
for generalized logistic function are given here under.Derivation of 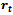 Consider,
Consider, 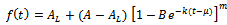 where
where 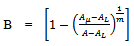 which can be rewritten as
which can be rewritten as 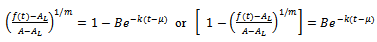 . Also, on differentiating
. Also, on differentiating 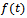 , we get
, we get 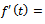
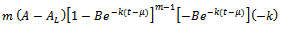
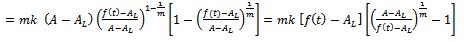
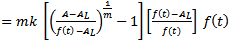 . On comparison of this
. On comparison of this 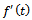 with
with 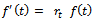 , we get
, we get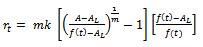 | (3) |
It is the Generalized Logistic relative growth rate function.Derivation of 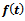 Put
Put 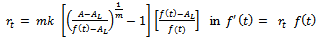 . Then, we get
. Then, we get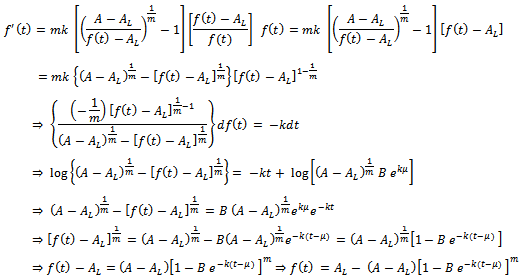 It is Generalized Logistic growth function. The integral constant in this case is
It is Generalized Logistic growth function. The integral constant in this case is 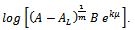
2.2. Particular Case of Logistic Function
A function called Particular Case of Logistic function is defined (Wikipedia) as 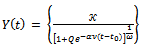 which we now re-express with same notations used in this paper as
which we now re-express with same notations used in this paper as 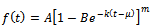 | (4) |
by replacing in the functions and other quantities using 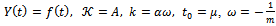 and
and 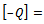
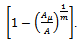 Note that the Generalized Logistic function with
Note that the Generalized Logistic function with 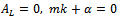 reduces to the Particular case of Logistic function. In the latter case, the parameter
reduces to the Particular case of Logistic function. In the latter case, the parameter 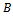 takes the form
takes the form 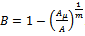 . Detailed derivations of the growth function
. Detailed derivations of the growth function 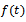 and therelative growth rate function
and therelative growth rate function 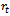 are given here under.Derivation of
are given here under.Derivation of 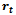 Consider
Consider 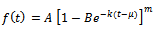 where
where 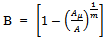 . It can be rewritten as
. It can be rewritten as 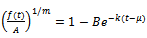 or equivalently
or equivalently 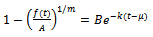 . Also, on differentiating
. Also, on differentiating 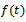 , we get
, we get 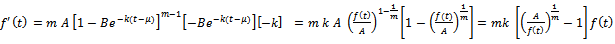 . On comparison of this
. On comparison of this 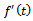 with
with 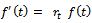 , we get
, we get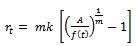 | (5) |
It is the relative growth rate function of Particular case of the generalized Logistic.Derivation of 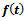 Put
Put 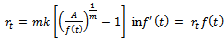 . Then, we get
. Then, we get 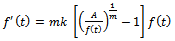
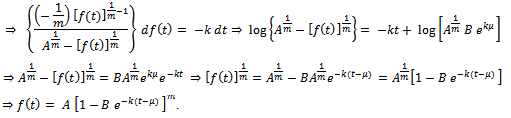 It is thegrowth function of Particular case of GeneralizedLogistic. The integral constant in thiscase is given by
It is thegrowth function of Particular case of GeneralizedLogistic. The integral constant in thiscase is given by 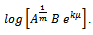
2.3. Richards Function
The Richards function is defined as in the usual notations (Richards, 1959) as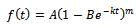 | (6) |
where 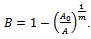 . The Richards function
. The Richards function 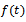 can be directly derived from the ODE or rate-state equation (1) with relative rate function
can be directly derived from the ODE or rate-state equation (1) with relative rate function 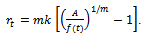 Derivation of
Derivation of 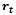 Consider
Consider 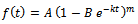 which can be rewritten as
which can be rewritten as 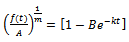 or equivalently we can write
or equivalently we can write 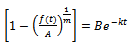 . Also on differentiating
. Also on differentiating 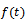 , we get
, we get 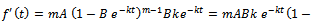
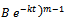 .On substituting all these in
.On substituting all these in 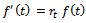 and simplifying, we get
and simplifying, we get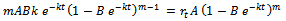
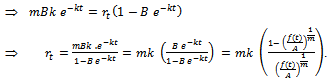 Hence
Hence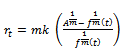 | (7) |
This is the required Richards expression for the relative growth rate function.Derivation of 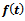 Put
Put 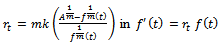 . Then, we get
. Then, we get 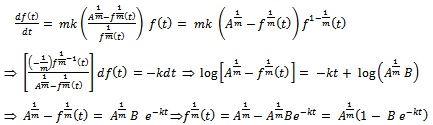
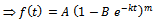 This is the required Richards expression for the growth function.Interpretation of B: Here
This is the required Richards expression for the growth function.Interpretation of B: Here 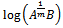 is the integral constant. Put
is the integral constant. Put 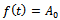 for
for 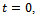 since
since 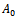 is the initial weight of an organism. Hence we get,
is the initial weight of an organism. Hence we get, 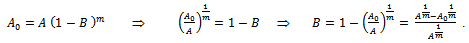
2.4. Von Bertalanffy Function
The Von Bertalanffy function is defined (Bertalanffy, 1957) as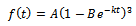 | (8) |
where 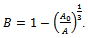 The Von Bertalanffy function is a special case of Richards function with
The Von Bertalanffy function is a special case of Richards function with 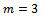 . The Von Bertalanffy function can be derived from ODE (1) given relative rate function. Derivation of
. The Von Bertalanffy function can be derived from ODE (1) given relative rate function. Derivation of 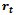 Consider
Consider 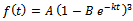 which can be rewritten as
which can be rewritten as 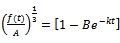 or equivalently rewritten as
or equivalently rewritten as 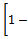
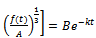 . Also, on differentiating
. Also, on differentiating 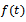 , we get
, we get 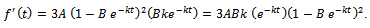 On substituting all the above in
On substituting all the above in 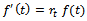 and simplifying, we get
and simplifying, we get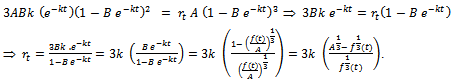 Hence
Hence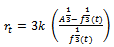 | (9) |
This 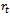 is the required Von Bertalanffy expression for the relative growth rate function.Derivation of
is the required Von Bertalanffy expression for the relative growth rate function.Derivation of 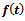 Put
Put 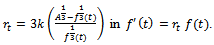 . Then, we get
. Then, we get 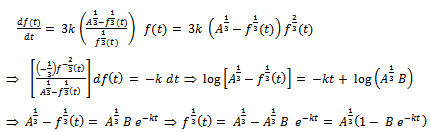
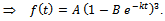 This is the required Von Bertalanffy expression for the growth function.Interpretation of B: Here
This is the required Von Bertalanffy expression for the growth function.Interpretation of B: Here 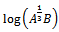 is the integral constant. Put
is the integral constant. Put 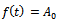 when
when 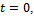 since
since 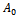 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get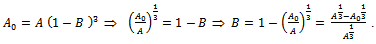
2.5. Brody Function
Brody is defined (Brody, 1945) as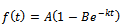 | (10) |
where 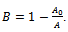 It is a special case ofRichards function with
It is a special case ofRichards function with 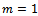 . It can also be derived from ODE (1) with given rate function. Derivation of
. It can also be derived from ODE (1) with given rate function. Derivation of 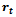 Consider
Consider 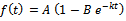 which can be rewritten as
which can be rewritten as 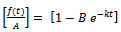 or equivalently we can write it as
or equivalently we can write it as 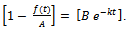 . Also, on differentiating
. Also, on differentiating 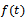 , we get
, we get 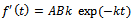 . On substituting all these in
. On substituting all these in 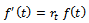 and simplifying, we get
and simplifying, we get 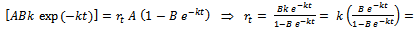
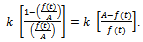 . That is,
. That is,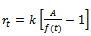 | (11) |
This is the required Gompertz expression for the relative growth rate function.Derivation of 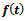 Put
Put 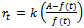 in
in 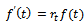 . Then, we get
. Then, we get 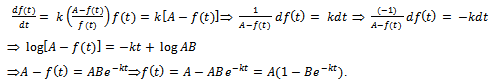 This is the required Gompertz expression for the growth function.Interpretation of B: Here
This is the required Gompertz expression for the growth function.Interpretation of B: Here 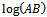 is the integral constant. Put
is the integral constant. Put 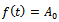 when
when 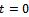 , since
, since 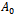 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get 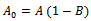 or equivalently
or equivalently 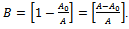 . Thus, B can be interpreted as the net amount of growth, resulted during the whole life period, per one unit of final (fruit) quantity.
. Thus, B can be interpreted as the net amount of growth, resulted during the whole life period, per one unit of final (fruit) quantity.
2.6. Classical Logistic Function
The classical Logistic function[6] is defined as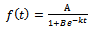 | (12) |
where 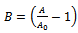 . The Logistic function is a special case of (i) Richards function (5) with
. The Logistic function is a special case of (i) Richards function (5) with 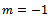 (ii) Particular case of logistic function (4) with
(ii) Particular case of logistic function (4) with 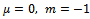 (ii) Generalized logistic function (3) with
(ii) Generalized logistic function (3) with 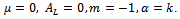 The Logistic function can be derived from the ODE (1). Detailed derivations are given below.Derivation of
The Logistic function can be derived from the ODE (1). Detailed derivations are given below.Derivation of 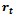 Consider,
Consider, 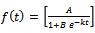 which can be rewritten as
which can be rewritten as 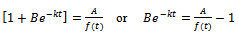 . Also, differentiating
. Also, differentiating 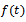 , we get
, we get 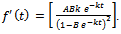 . On substituting all these in
. On substituting all these in 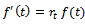 and after simplification we get
and after simplification we get 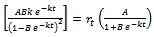
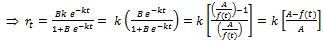 . That is,
. That is,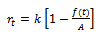 | (13) |
This is the required Logistic expression for the relative growth rate function.Derivation of 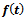 Putting
Putting 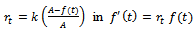 we get
we get 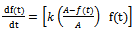 or equivalently
or equivalently 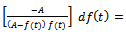
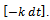 . Using partial fractions, it reduces to
. Using partial fractions, it reduces to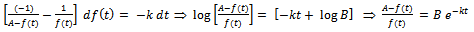
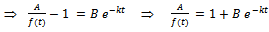 . This is the required Logistic expression for the growth function.Interpretation of B: Here
. This is the required Logistic expression for the growth function.Interpretation of B: Here 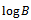 is the integral constant. Put
is the integral constant. Put 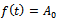 when
when 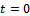 , since
, since 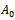 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get 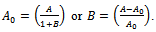 . Therefore, B is interpreted as the ‘Net amount of growth’, resulted during the life period per one unit of initial (seed) quantity.
. Therefore, B is interpreted as the ‘Net amount of growth’, resulted during the life period per one unit of initial (seed) quantity.
2.7. Gompertz Function
The Gompertz function (Winsor, 1932) is defined as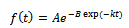 | (14) |
where 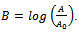 It can be shown thatGompertz function a special case of (i) Richards function with
It can be shown thatGompertz function a special case of (i) Richards function with 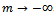 (ii) Particular case of logistic function with
(ii) Particular case of logistic function with 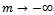 and (iii)Generalized logistic function with
and (iii)Generalized logistic function with 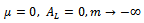 ,
, 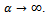 The Gompertz function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of
The Gompertz function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of 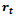 Consider
Consider 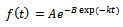 ,
, 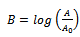 and can be rewritten as
and can be rewritten as 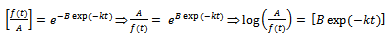 . Also, on differentiating
. Also, on differentiating 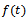 , we get
, we get 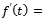
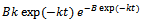 . On substituting all these in
. On substituting all these in 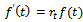 and after simplification we get
and after simplification we get 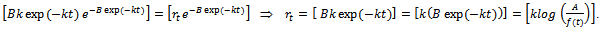 Thus
Thus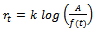 | (15) |
This is the required Gompertz expression for the relative growth rate function.Derivation of 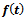 Put
Put 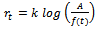 in
in 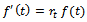 . Then, we get
. Then, we get 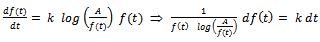
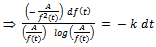
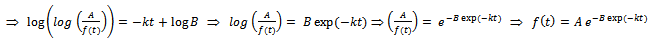 . This is the required Gompertz expression for the growth function.Interpretation of B: Here
. This is the required Gompertz expression for the growth function.Interpretation of B: Here 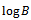 is the integral constant. Put
is the integral constant. Put 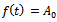 when
when 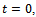 since
since 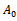 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get 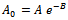 or equivalently
or equivalently 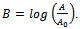 Thus, B can be interpreted as the logarithm of the total amount of growth, resulted during the whole life period, per one unit of initial (seed) quantity.
Thus, B can be interpreted as the logarithm of the total amount of growth, resulted during the whole life period, per one unit of initial (seed) quantity.
2.8. Weibull Function
The Weibull growth model[13] is given as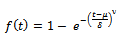 | (16) |
and this function can be derived from the ODE (1) with rate function. Detailed derivations of this function 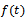 and relative growth rate
and relative growth rate 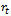 are given below.Derivation of
are given below.Derivation of 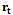 Consider
Consider 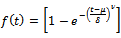 and can be rewritten as
and can be rewritten as 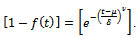 Also, on differentiating
Also, on differentiating 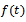 , we get
, we get 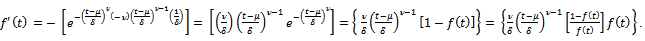 . On comparing this with
. On comparing this with 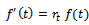 we get,
we get, 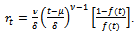 Thus
Thus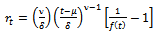 | (17) |
This is the required relative growth rate function for Weibull.Derivation of 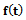 Put
Put 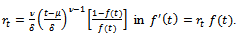 Then, we get
Then, we get 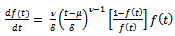 or equivalently it can be written as
or equivalently it can be written as 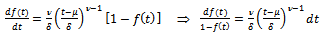
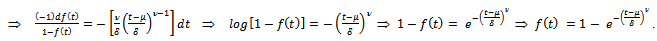 . This is the Weibull growth function.Note that here the integral constant is taken to be zero.
. This is the Weibull growth function.Note that here the integral constant is taken to be zero.
2.9. Generalized Weibull Function
The Weibull function is generalized and named here asGeneralized Weibull function and is defined as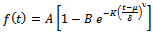 | (18) |
where 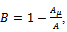 with the same notations used in this paper. Note that the Weibull a special case of Generalized Weibull function with
with the same notations used in this paper. Note that the Weibull a special case of Generalized Weibull function with 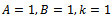 . Generalized Weibull function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of
. Generalized Weibull function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of 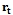 Consider
Consider 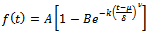 which can be rewritten as
which can be rewritten as 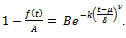 Also, on differentiating
Also, on differentiating 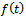 with respect to t, we get
with respect to t, we get 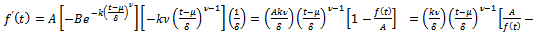
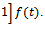 . On comparison of this with
. On comparison of this with 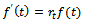 we get
we get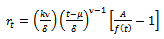 | (19) |
This is the required relative growth rate function for Weibull.Derivation of 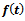
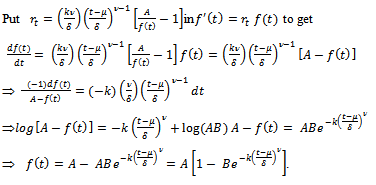 This is the Generalized Weibull growth function. Note that here the integral constant is taken to be
This is the Generalized Weibull growth function. Note that here the integral constant is taken to be 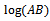 .
.Table 1. List of Growth Functions with their Respective RelativeGrowth Rate Functions, Expressions for Parameter B and Integral Constants
 |
| |
|
2.10. Monomolecular and Mitscherlich Functions
The Monomolecular growth function is defined[15], in its original notations, as 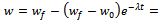
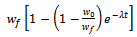 where
where 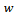 is the growth function at time
is the growth function at time 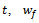 is the final (mature) value,
is the final (mature) value, 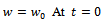 is the initial value and
is the initial value and 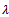 is the growth rate. This function can be expressed as Brody function
is the growth rate. This function can be expressed as Brody function 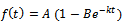 by considering the parametric transformation
by considering the parametric transformation 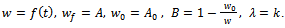 Derivations of
Derivations of 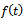 and
and 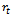 follow same as equations (10) and (11). Mitscherlich growth function[20] is defined, in its original notations, as
follow same as equations (10) and (11). Mitscherlich growth function[20] is defined, in its original notations, as 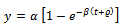 where
where 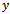 is the growth function,
is the growth function, 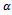 is the final (mature) growth,
is the final (mature) growth, 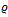 is a constant and
is a constant and 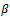 is rate of growth. The Mitscherlich function can be expressed as Brody
is rate of growth. The Mitscherlich function can be expressed as Brody 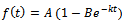 ) by considering the parametric transformation as
) by considering the parametric transformation as 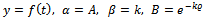 . It can be derived from the ODE (1) that the rate function as
. It can be derived from the ODE (1) that the rate function as 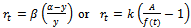 . Not that the integral constant here reduces to
. Not that the integral constant here reduces to 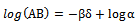 . Similarly, derivations of
. Similarly, derivations of 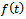 and
and 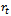 follow same as equations (10) and (11).
follow same as equations (10) and (11).
3. Conclusions
In this paper, the commonly used biological growth models are considered and explicitly shown that each is a solution of the rate-state ordinary differential equation 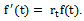 The formula for
The formula for 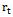 and
and 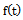 are constructed as solutions of the rate-state equation describing the growth models for each of the functions: generalized logistic, the particular case of the generalized logistic, Richards, von Bertalanffy, Brody, classical logistic, Gompertz, Weibull, generalized Weibull, monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians in applied fields such as Biological sciences. All the growth functions discussed are displayed in Table 1 together with respective relative growth rate functions, expression for parameter
are constructed as solutions of the rate-state equation describing the growth models for each of the functions: generalized logistic, the particular case of the generalized logistic, Richards, von Bertalanffy, Brody, classical logistic, Gompertz, Weibull, generalized Weibull, monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians in applied fields such as Biological sciences. All the growth functions discussed are displayed in Table 1 together with respective relative growth rate functions, expression for parameter 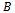 and integral constant. We note that there is a restriction on the acceptable values of
and integral constant. We note that there is a restriction on the acceptable values of 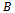 in each of the models. Further, the rate-state equation is capable of generating still more general and useful solutions. We will explore the possibility of constructing such models, relationships among the models and their inflection points.
in each of the models. Further, the rate-state equation is capable of generating still more general and useful solutions. We will explore the possibility of constructing such models, relationships among the models and their inflection points.
References
| [1] | S. Brody, Bioenergetics and growth, Rheinhold Pub. Corp. N.Y., 1945. |
| [2] | Von L. Bertalanffy, Quantitative laws in metabolism and growth, Quart. Rev. Biol. 3-2 (1957) 218. |
| [3] | F.J. Richards, A flexible growth function for empirical use. J. Exp. Bot. 10 (1959) 290-300. |
| [4] | J. France, J.H.M. Thornley, Mathematical models in agriculture, Butterworths, London, 335, 1984. |
| [5] | C.P. Winsor, The Gompertz curve as a growth curve, Proc. National Academy of Science, 18 (1932) 1. |
| [6] | J.A. Nelder, The fitting of a generalization of the logistic curve, Biometrics 17 (1961) 89-110. |
| [7] | J.E. Brown, H.A. Fitzhugh, Jr., T.C. Cartwright, A Comparison of nonlinear models for describing weight-age relationship in cattle. J. Animal Sci. 42 (1976) 810-818. |
| [8] | T.B. Robertson, On the normal rate of growth of an individual and its biochemical significance, Arch Entwicklungsmech Org 25 (1906) 581-614. |
| [9] | L.L. Eberhardt and J.M. Breiwick, Models for population growth curves. International Scholarly Research Network, ISRN Ecology 2012 (2012), doi:10.5402/2012/815016. |
| [10] | D. Fekedulegn, M.P. Mac Siurtain, J.J. Colbert, Parameter estimation of nonlinear growth models in forestry, Silva Fennica 33-4 (1999) 327-336. |
| [11] | F.J. Ayala, M.E. Gilpin, J.G. Ehrenfeld, Competition between species: theoretical models and experimental tests. Theoretical Population Biology, 4-3 (1973) 331-356. |
| [12] | J.O. Rawlings, W.W. Cure, The Weibull function as a dose response model for air pollution effects on crop yields. Crop Science 25 (1985) 807-814. |
| [13] | J.O. Rawlings, S.G. Pantula, D.A. Dickey, Applied regression analysis: a research tool, Second Edition, 1998. |
| [14] | W.J. Spillman, E. Lang, The law of diminishing increment, World, Yonkers, 1924. |
| [15] | J. France, J. Dijkstra, M.S. MDhanoa, Growth functions and their application in animal science, Ann. Zootechn 45 (1996) 165-174. |
| [16] | İ.E. Ersoy, M. Mendeş, S. Keskin, Estimation of parameters of linear and nonlinear growth curve models at early growth stage in California Turkeys, Arch. Geflügelk. 71-4 (2007) 175–180. |
| [17] | Y.C. Lei, S.Y. Zhang, Features and partial derivatives of bertalanffy-richards growth model in forestry. Nonlinear Analysis: Modelling and Control 9-1 (2004) 65-73. |
| [18] | B. Zeide, Analysis of growth equations, Forest Science, 39-3 (1993) 594-616. |
| [19] | http://en.wikipedia.org/w/index.php?oldid=472125857 (accessed on December 2012). |
| [20] | R.A. Mombiela, L.A. Nelson, Relationships among some biological and empirical fertilizer response models and use of the power family of transformations to identify an appropriate model. Agronomy Journal 73 (1981) 353-356. |
| [21] | C.H. Edwards, Jr, D.E. Penney, Calculus with analytic geometry, Printice Hall International, New Jersey, 1994. |
| [22] | R. Ellis, D. Gulick, Calculus with analytic geometry, Harcourt Brace Jovanovich Pub., USA, 1986. |

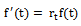 which describes biological growths.We construct growth function
which describes biological growths.We construct growth function 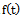 and relative growth function
and relative growth function 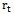 for the models: Generalized logistic, Particular case of generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians working in the fields of Biological sciences and non-availability of these derivations in literature.
for the models: Generalized logistic, Particular case of generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians working in the fields of Biological sciences and non-availability of these derivations in literature.
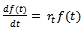
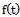 is representing growth function and
is representing growth function and 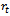 is relative rate function at time
is relative rate function at time 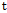 . This ordinary differential equation has many solutions among which some are studied here. The purpose of this paper is to explicitly show that the commonly used growth models are solutions of the rate-state equation by constructing
. This ordinary differential equation has many solutions among which some are studied here. The purpose of this paper is to explicitly show that the commonly used growth models are solutions of the rate-state equation by constructing 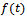 and
and 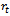 .In the current paper, detailed derivations of
.In the current paper, detailed derivations of 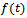 and
and 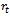 are presented considering non mathematicians working in the fields of Biological sciences and non availability of these derivations in the literature. All the growth functions discussed here are displayed in Table 1 together with respective relative growth rate functions, expression for
are presented considering non mathematicians working in the fields of Biological sciences and non availability of these derivations in the literature. All the growth functions discussed here are displayed in Table 1 together with respective relative growth rate functions, expression for 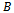 and integral constant.
and integral constant.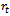 and
and 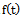 . The growth curves considered in this paper are: Generalized logistic, Particular case of the generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich functions.
. The growth curves considered in this paper are: Generalized logistic, Particular case of the generalized logistic, Richards, Von Bertalanffy, Brody, Classical logistic, Gompertz, Weibull, Generalized Weibull, Monomolecular and Mitscherlich functions.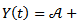
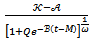 which we now re-express in the same notations used in this paper as
which we now re-express in the same notations used in this paper as 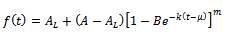
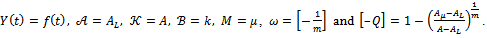 Detailed derivations of
Detailed derivations of 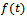 and
and 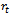 for generalized logistic function are given here under.Derivation of
for generalized logistic function are given here under.Derivation of 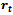 Consider,
Consider, 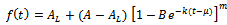 where
where 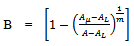 which can be rewritten as
which can be rewritten as 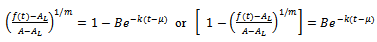 . Also, on differentiating
. Also, on differentiating 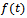 , we get
, we get 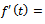
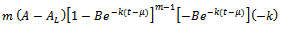
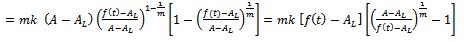
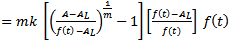 . On comparison of this
. On comparison of this 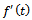 with
with 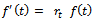 , we get
, we get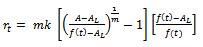
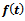 Put
Put 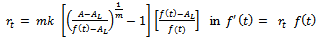 . Then, we get
. Then, we get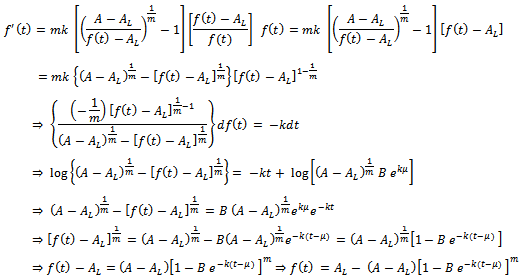 It is Generalized Logistic growth function. The integral constant in this case is
It is Generalized Logistic growth function. The integral constant in this case is 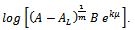
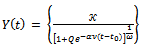 which we now re-express with same notations used in this paper as
which we now re-express with same notations used in this paper as 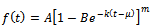
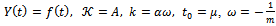 and
and 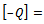
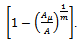 Note that the Generalized Logistic function with
Note that the Generalized Logistic function with 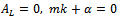 reduces to the Particular case of Logistic function. In the latter case, the parameter
reduces to the Particular case of Logistic function. In the latter case, the parameter 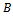 takes the form
takes the form 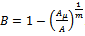 . Detailed derivations of the growth function
. Detailed derivations of the growth function 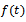 and therelative growth rate function
and therelative growth rate function 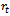 are given here under.Derivation of
are given here under.Derivation of 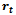 Consider
Consider 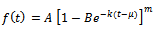 where
where 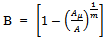 . It can be rewritten as
. It can be rewritten as 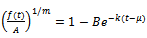 or equivalently
or equivalently 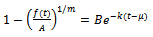 . Also, on differentiating
. Also, on differentiating 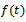 , we get
, we get 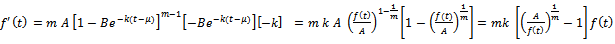 . On comparison of this
. On comparison of this 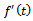 with
with 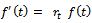 , we get
, we get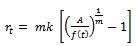
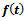 Put
Put 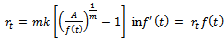 . Then, we get
. Then, we get 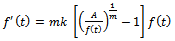
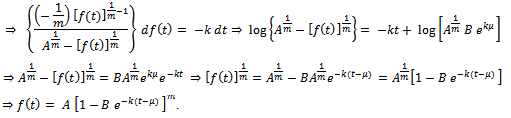 It is thegrowth function of Particular case of GeneralizedLogistic. The integral constant in thiscase is given by
It is thegrowth function of Particular case of GeneralizedLogistic. The integral constant in thiscase is given by 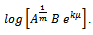
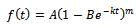
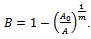 . The Richards function
. The Richards function 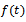 can be directly derived from the ODE or rate-state equation (1) with relative rate function
can be directly derived from the ODE or rate-state equation (1) with relative rate function 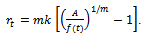 Derivation of
Derivation of 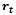 Consider
Consider 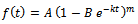 which can be rewritten as
which can be rewritten as 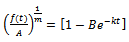 or equivalently we can write
or equivalently we can write 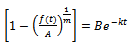 . Also on differentiating
. Also on differentiating 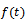 , we get
, we get 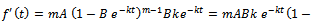
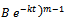 .On substituting all these in
.On substituting all these in 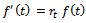 and simplifying, we get
and simplifying, we get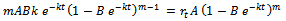
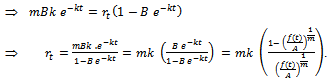 Hence
Hence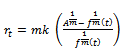
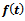 Put
Put 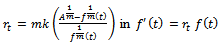 . Then, we get
. Then, we get 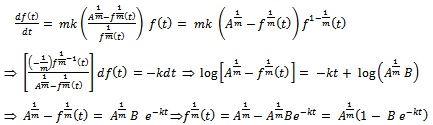
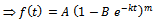 This is the required Richards expression for the growth function.Interpretation of B: Here
This is the required Richards expression for the growth function.Interpretation of B: Here 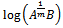 is the integral constant. Put
is the integral constant. Put 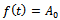 for
for 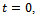 since
since 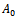 is the initial weight of an organism. Hence we get,
is the initial weight of an organism. Hence we get, 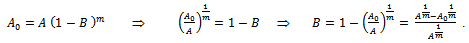
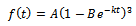
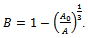 The Von Bertalanffy function is a special case of Richards function with
The Von Bertalanffy function is a special case of Richards function with 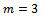 . The Von Bertalanffy function can be derived from ODE (1) given relative rate function. Derivation of
. The Von Bertalanffy function can be derived from ODE (1) given relative rate function. Derivation of 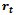 Consider
Consider 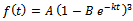 which can be rewritten as
which can be rewritten as 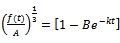 or equivalently rewritten as
or equivalently rewritten as 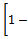
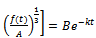 . Also, on differentiating
. Also, on differentiating 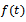 , we get
, we get 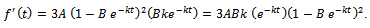 On substituting all the above in
On substituting all the above in 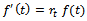 and simplifying, we get
and simplifying, we get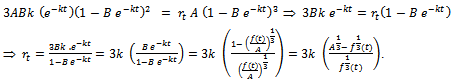 Hence
Hence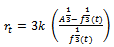
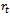 is the required Von Bertalanffy expression for the relative growth rate function.Derivation of
is the required Von Bertalanffy expression for the relative growth rate function.Derivation of 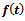 Put
Put 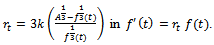 . Then, we get
. Then, we get 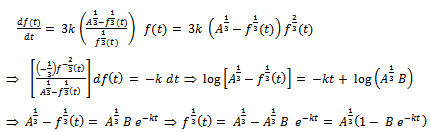
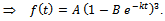 This is the required Von Bertalanffy expression for the growth function.Interpretation of B: Here
This is the required Von Bertalanffy expression for the growth function.Interpretation of B: Here 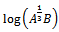 is the integral constant. Put
is the integral constant. Put 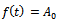 when
when 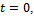 since
since 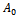 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get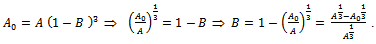
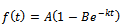
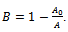 It is a special case ofRichards function with
It is a special case ofRichards function with 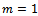 . It can also be derived from ODE (1) with given rate function. Derivation of
. It can also be derived from ODE (1) with given rate function. Derivation of 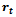 Consider
Consider 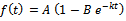 which can be rewritten as
which can be rewritten as 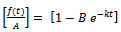 or equivalently we can write it as
or equivalently we can write it as 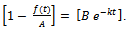 . Also, on differentiating
. Also, on differentiating 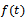 , we get
, we get 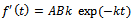 . On substituting all these in
. On substituting all these in 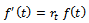 and simplifying, we get
and simplifying, we get 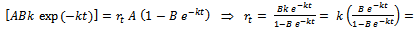
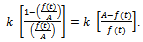 . That is,
. That is,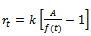
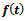 Put
Put 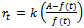 in
in 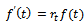 . Then, we get
. Then, we get 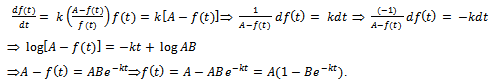 This is the required Gompertz expression for the growth function.Interpretation of B: Here
This is the required Gompertz expression for the growth function.Interpretation of B: Here 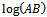 is the integral constant. Put
is the integral constant. Put 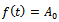 when
when 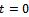 , since
, since 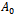 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get 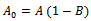 or equivalently
or equivalently 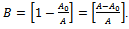 . Thus, B can be interpreted as the net amount of growth, resulted during the whole life period, per one unit of final (fruit) quantity.
. Thus, B can be interpreted as the net amount of growth, resulted during the whole life period, per one unit of final (fruit) quantity.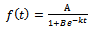
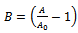 . The Logistic function is a special case of (i) Richards function (5) with
. The Logistic function is a special case of (i) Richards function (5) with 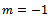 (ii) Particular case of logistic function (4) with
(ii) Particular case of logistic function (4) with 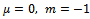 (ii) Generalized logistic function (3) with
(ii) Generalized logistic function (3) with 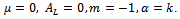 The Logistic function can be derived from the ODE (1). Detailed derivations are given below.Derivation of
The Logistic function can be derived from the ODE (1). Detailed derivations are given below.Derivation of 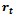 Consider,
Consider, 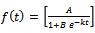 which can be rewritten as
which can be rewritten as 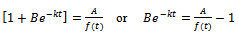 . Also, differentiating
. Also, differentiating 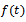 , we get
, we get 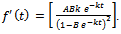 . On substituting all these in
. On substituting all these in 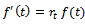 and after simplification we get
and after simplification we get 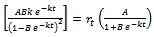
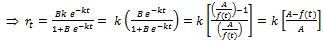 . That is,
. That is,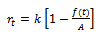
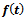 Putting
Putting 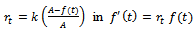 we get
we get 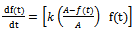 or equivalently
or equivalently 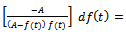
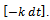 . Using partial fractions, it reduces to
. Using partial fractions, it reduces to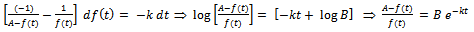
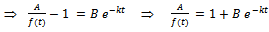 . This is the required Logistic expression for the growth function.Interpretation of B: Here
. This is the required Logistic expression for the growth function.Interpretation of B: Here 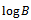 is the integral constant. Put
is the integral constant. Put 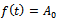 when
when 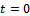 , since
, since 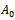 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get 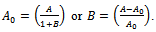 . Therefore, B is interpreted as the ‘Net amount of growth’, resulted during the life period per one unit of initial (seed) quantity.
. Therefore, B is interpreted as the ‘Net amount of growth’, resulted during the life period per one unit of initial (seed) quantity.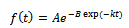
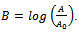 It can be shown thatGompertz function a special case of (i) Richards function with
It can be shown thatGompertz function a special case of (i) Richards function with 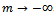 (ii) Particular case of logistic function with
(ii) Particular case of logistic function with 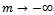 and (iii)Generalized logistic function with
and (iii)Generalized logistic function with 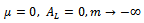 ,
, 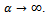 The Gompertz function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of
The Gompertz function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of 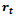 Consider
Consider 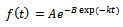 ,
, 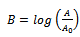 and can be rewritten as
and can be rewritten as 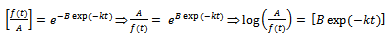 . Also, on differentiating
. Also, on differentiating 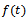 , we get
, we get 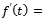
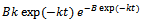 . On substituting all these in
. On substituting all these in 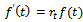 and after simplification we get
and after simplification we get 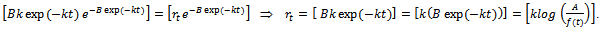 Thus
Thus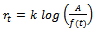
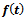 Put
Put 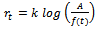 in
in 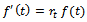 . Then, we get
. Then, we get 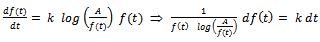
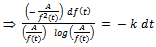
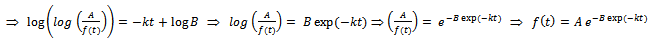 . This is the required Gompertz expression for the growth function.Interpretation of B: Here
. This is the required Gompertz expression for the growth function.Interpretation of B: Here 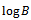 is the integral constant. Put
is the integral constant. Put 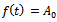 when
when 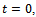 since
since 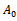 is the initial weight of an organism. Thus, we get
is the initial weight of an organism. Thus, we get 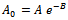 or equivalently
or equivalently 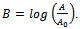 Thus, B can be interpreted as the logarithm of the total amount of growth, resulted during the whole life period, per one unit of initial (seed) quantity.
Thus, B can be interpreted as the logarithm of the total amount of growth, resulted during the whole life period, per one unit of initial (seed) quantity.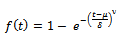
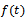 and relative growth rate
and relative growth rate 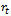 are given below.Derivation of
are given below.Derivation of 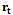 Consider
Consider 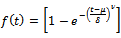 and can be rewritten as
and can be rewritten as 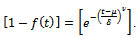 Also, on differentiating
Also, on differentiating 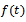 , we get
, we get 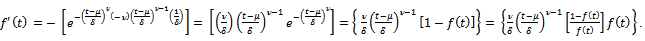 . On comparing this with
. On comparing this with 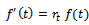 we get,
we get, 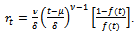 Thus
Thus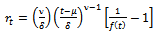
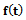 Put
Put 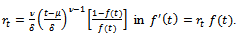 Then, we get
Then, we get 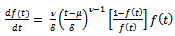 or equivalently it can be written as
or equivalently it can be written as 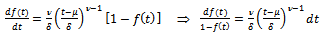
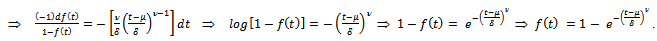 . This is the Weibull growth function.Note that here the integral constant is taken to be zero.
. This is the Weibull growth function.Note that here the integral constant is taken to be zero.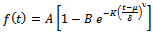
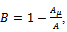 with the same notations used in this paper. Note that the Weibull a special case of Generalized Weibull function with
with the same notations used in this paper. Note that the Weibull a special case of Generalized Weibull function with 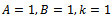 . Generalized Weibull function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of
. Generalized Weibull function can be derived from the ODE (1) with given rate function. Detailed derivations are given below.Derivation of 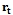 Consider
Consider 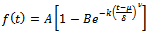 which can be rewritten as
which can be rewritten as 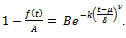 Also, on differentiating
Also, on differentiating 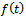 with respect to t, we get
with respect to t, we get 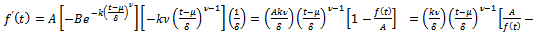
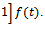 . On comparison of this with
. On comparison of this with 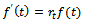 we get
we get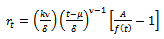
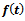
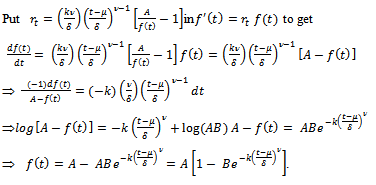 This is the Generalized Weibull growth function. Note that here the integral constant is taken to be
This is the Generalized Weibull growth function. Note that here the integral constant is taken to be 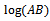 .
.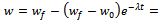
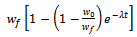 where
where 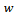 is the growth function at time
is the growth function at time 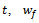 is the final (mature) value,
is the final (mature) value, 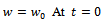 is the initial value and
is the initial value and 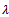 is the growth rate. This function can be expressed as Brody function
is the growth rate. This function can be expressed as Brody function 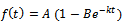 by considering the parametric transformation
by considering the parametric transformation 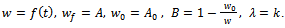 Derivations of
Derivations of 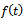 and
and 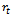 follow same as equations (10) and (11). Mitscherlich growth function[20] is defined, in its original notations, as
follow same as equations (10) and (11). Mitscherlich growth function[20] is defined, in its original notations, as 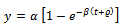 where
where 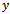 is the growth function,
is the growth function, 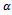 is the final (mature) growth,
is the final (mature) growth, 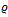 is a constant and
is a constant and 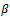 is rate of growth. The Mitscherlich function can be expressed as Brody
is rate of growth. The Mitscherlich function can be expressed as Brody 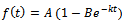 ) by considering the parametric transformation as
) by considering the parametric transformation as 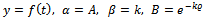 . It can be derived from the ODE (1) that the rate function as
. It can be derived from the ODE (1) that the rate function as 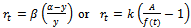 . Not that the integral constant here reduces to
. Not that the integral constant here reduces to 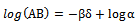 . Similarly, derivations of
. Similarly, derivations of 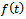 and
and 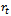 follow same as equations (10) and (11).
follow same as equations (10) and (11).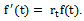 The formula for
The formula for 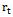 and
and 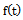 are constructed as solutions of the rate-state equation describing the growth models for each of the functions: generalized logistic, the particular case of the generalized logistic, Richards, von Bertalanffy, Brody, classical logistic, Gompertz, Weibull, generalized Weibull, monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians in applied fields such as Biological sciences. All the growth functions discussed are displayed in Table 1 together with respective relative growth rate functions, expression for parameter
are constructed as solutions of the rate-state equation describing the growth models for each of the functions: generalized logistic, the particular case of the generalized logistic, Richards, von Bertalanffy, Brody, classical logistic, Gompertz, Weibull, generalized Weibull, monomolecular and Mitscherlich. Detailed derivations are presented considering non-mathematicians in applied fields such as Biological sciences. All the growth functions discussed are displayed in Table 1 together with respective relative growth rate functions, expression for parameter 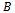 and integral constant. We note that there is a restriction on the acceptable values of
and integral constant. We note that there is a restriction on the acceptable values of 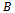 in each of the models. Further, the rate-state equation is capable of generating still more general and useful solutions. We will explore the possibility of constructing such models, relationships among the models and their inflection points.
in each of the models. Further, the rate-state equation is capable of generating still more general and useful solutions. We will explore the possibility of constructing such models, relationships among the models and their inflection points. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML