Oyekan E. A.1, Opoola T. O.2
1Department of Mathematics and Statistics, Bowen University, Iwo, 23001, Nigeria
2Department Mathematics, University of Ilorin, Ilorin, 240001, Nigeria
Correspondence to: Oyekan E. A., Department of Mathematics and Statistics, Bowen University, Iwo, 23001, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Functions belonging to each of the subclasses 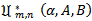 and
and 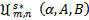 of normalized analytic functions in the open unit disk
of normalized analytic functions in the open unit disk 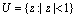 are investigated when
are investigated when 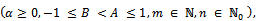 and several subordinations are obtained. A number of interesting consequences of these subordination results are also discussed.
and several subordinations are obtained. A number of interesting consequences of these subordination results are also discussed.
Keywords:
Subordination, Analytic Functions, Salagean Operator, Subordinating Factor Sequence, Hadamard Product (or Convolution)
Cite this paper: Oyekan E. A., Opoola T. O., Some Subordination Results for Certain Subclasses of Analytic Functions Defined by Using Salagean Operator, American Journal of Mathematics and Statistics, Vol. 3 No. 6, 2013, pp. 301-304. doi: 10.5923/j.ajms.20130306.01.
1. Introduction and Definitions
Let denote the class of functions of the form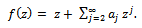 | (1.1) |
Which are analytic in the unit disk 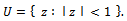 Shu-Hai and Tang in 2010[1], introduced the classes
Shu-Hai and Tang in 2010[1], introduced the classes 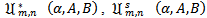 and gave the following definition:Definition 1. Let
and gave the following definition:Definition 1. Let 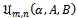 denote the subclass of
denote the subclass of 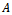 consisting of functions
consisting of functions 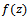 which satisfy the following inequality:
which satisfy the following inequality: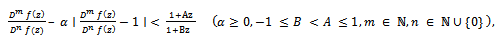 | (1.2) |
Definition 2. Let 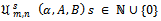 be the subclass of
be the subclass of 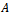 consisting of function
consisting of function 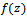 which satisfy the following condition:
which satisfy the following condition: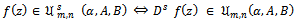 | (1.3) |
Where 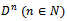 is the Salagean derivative operator defined as:
is the Salagean derivative operator defined as: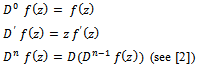 For
For 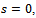 it is easy to see that
it is easy to see that  We denote by k the class of convex functions i.e.
We denote by k the class of convex functions i.e. Definition 3. (Hadamard product or convolution) Given two functions
Definition 3. (Hadamard product or convolution) Given two functions 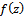 and
and 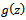 where
where 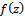 is as defined in (1.1) and
is as defined in (1.1) and 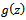 is given by
is given by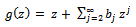 | (1.4) |
The Hadamard product (or convolution) 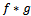 of
of 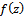 and
and 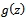 is defined by
is defined by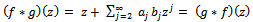 | (1.5) |
Definition 4. (Subordination principle)Let 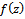 and
and 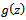 be analytic in the unit disk
be analytic in the unit disk 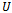 . Then
. Then 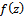 is said to be subordinate to
is said to be subordinate to 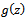 in
in 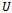 and we write
and we write 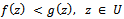 , if there exists a Schwarz function
, if there exists a Schwarz function 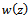 , analytic in
, analytic in 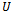 with
with 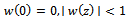 such that
such that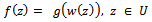 | (1.6) |
In particular, if the function 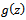 is univalent in
is univalent in 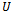 , then
, then 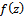 is subordinate to
is subordinate to 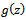 if
if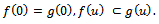 | (1.7) |
Definition 5. (Subordinating factor sequence)A sequence 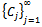 of complex numbers is said to be a subordinating factor sequence if whenever
of complex numbers is said to be a subordinating factor sequence if whenever 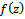 of the form (1.1) is analytic, univalent and convex in
of the form (1.1) is analytic, univalent and convex in 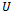 , the subordination is given by
, the subordination is given by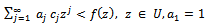 We have the following theoremTheorem 1.1 (Wilf [3])The sequence
We have the following theoremTheorem 1.1 (Wilf [3])The sequence 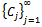 is a subordinating factor sequence if and only if
is a subordinating factor sequence if and only if 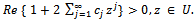 | (1.8) |
Theorem 1.2. [1]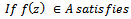
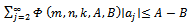 | (1.9) |
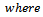
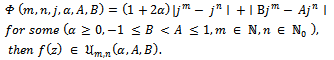 | (1.10) |
Theorem 1.3. [1]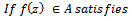
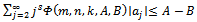 | (1.11) |
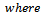
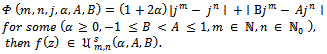 | (1.12) |
In view of Theorem 1.2 and Theorem 1.3, we now introduce the subclasses 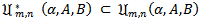 and
and 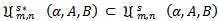 which consist of functions
which consist of functions 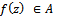 whose Taylor-Maclaurin coefficients
whose Taylor-Maclaurin coefficients 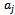 satisfy the inequalities (1.9) and (1.11) respectively.In our proposed investigation of functions in the classes
satisfy the inequalities (1.9) and (1.11) respectively.In our proposed investigation of functions in the classes 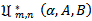 and
and 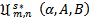 we obtain sharp subordination results for these classes and also investigate some applications of the main results which give important results of analytic functions.
we obtain sharp subordination results for these classes and also investigate some applications of the main results which give important results of analytic functions.
2. Main Theorem
Subordination results for the class 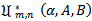 Theorem 2.1. Let
Theorem 2.1. Let 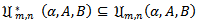
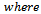
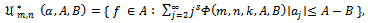 | (2.1) |
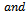
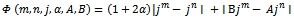
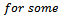
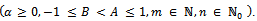
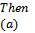
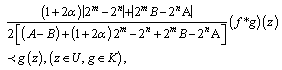 | (2.2) |
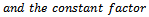
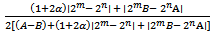 | (2.3) |
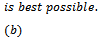
 | (2.4) |
PROOF OF THEOREM 2.1Let 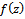 defined by (1.1) be any member of the class
defined by (1.1) be any member of the class 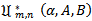 and suppose that
and suppose that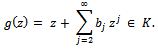 Then
Then 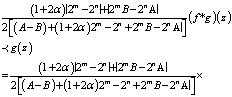 | (2.5) |
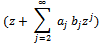 Thus, by Definition 5 the subordination (2.2) will hold if the sequence,
Thus, by Definition 5 the subordination (2.2) will hold if the sequence,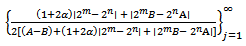 | (2.6) |
is a subordinating factor sequence with 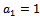 .Therefore by Theorem 1.1, it is sufficient to show that
.Therefore by Theorem 1.1, it is sufficient to show that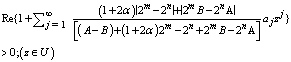 | (2.7) |
Now,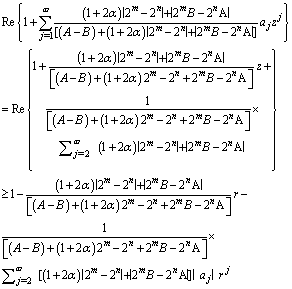 | (2.8) |
because 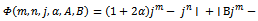 is an increasing function of
is an increasing function of 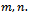 Thus,
Thus, | (2.9) |
Thus, (2.4) holds true in U and consequently proves (2.2).Next we show that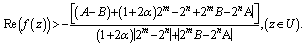 Now taking
Now taking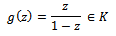 and
and 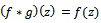 in (2.2) we have that
in (2.2) we have that 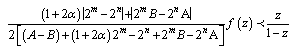 | (2.10) |
Therefore since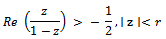
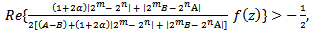 | (2.11) |
which implies that 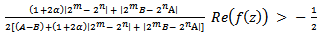 | (2.12) |
Hence, we have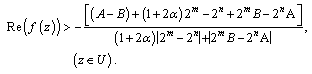 For
For 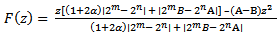 | (2.13) |
By max/min principle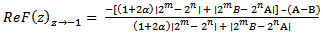 | (2.14) |
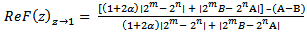 | (2.15) |
Hence,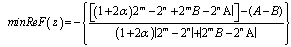 | (2.16) |
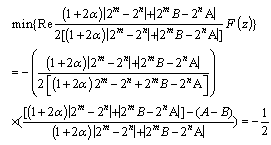 | (2.17) |
which shows that the constant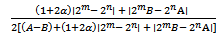 is the best possible and thus complete the proof of theorem 2.1.Subordination result for the class
is the best possible and thus complete the proof of theorem 2.1.Subordination result for the class 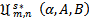 Our proof of Theorem 2.2 below is much akin to that of Theorem 2.1. Here we make use of Theorem 1.3 in place of Theorem 1.2 and let
Our proof of Theorem 2.2 below is much akin to that of Theorem 2.1. Here we make use of Theorem 1.3 in place of Theorem 1.2 and let 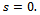 Theorem 2.2. Let
Theorem 2.2. Let 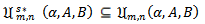
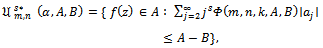 | (2.18) |
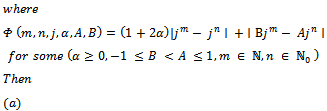
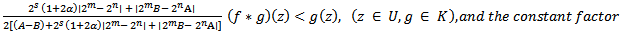 | (2.19) |
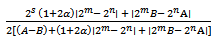 | (2.20) |
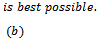
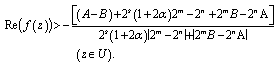 | (2.21) |
3. Some Applications
Taking 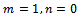 in Theorem 2.1; we obtain the following:Corollary1.
in Theorem 2.1; we obtain the following:Corollary1. 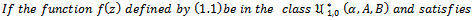
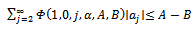 | (3.1) |
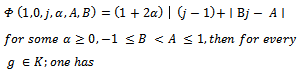
 | (3.2) |
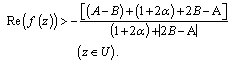 | (3.3) |
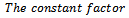
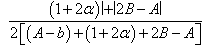
 Remark 1:
Remark 1: and Karthikenyan[5], and singh[6]
and Karthikenyan[5], and singh[6]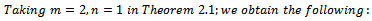 Corollary2.
Corollary2. 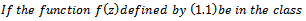
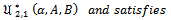
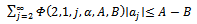 | (3.4) |
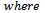
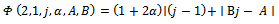
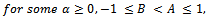
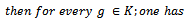
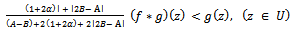 | (3.5) |
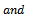
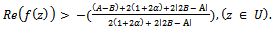 | (3.6) |
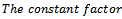
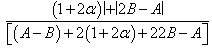
 Remark 2:The case
Remark 2:The case 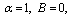 and
and 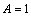 was obtained by Frasin [4], and Selvaraj and Karthikeyan [5].and Karthikeyan [5]
was obtained by Frasin [4], and Selvaraj and Karthikeyan [5].and Karthikeyan [5]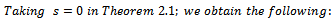
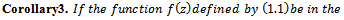
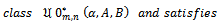
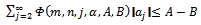 | (3.7) |
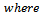
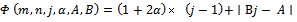
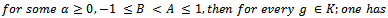
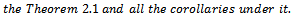
References
| [1] | Shu – Hai Li and Tang, H., “Certain New Classes of analytic Functions defined by using Salagean operator,” Bulletin of Mathematical Analysis and Applications, Vol. 2, Issue 4, pp. 62-75, 2010. |
| [2] | S˘al˘agean, G..S., “Subclasses of univalent functions,” Lecture Notes in Math. Springer-Verlag,” 1013, pp. 362–372, 1983. |
| [3] | Wilf, H.S. “Subordinating factor sequences for some convex maps of unit circle,” Proceedings of the American Mathematical society, Vol. 12, pp. 689-693, 1961. |
| [4] | Frasin, B.A., “Subordination results for class of analytic functions defined by a linear operator,” Journal of Inequalities in Pure and Applied Mathematics, Vol. 7. Issue 4, Article 134, pp 1-7, 2006. |
| [5] | Selvaraj, C. and karthikeyan, K.R., “Certain Subordination Results for a Class of Analytic Functions Defined by a Generalized Integral Operator, International Journal of Computational and mathematical Sciences, 2, pp 166-168, 2008. |
| [6] | Sukhjit Singh, “A Subordination Theorem for Spiral-like Functions,” International Journal of Mathematics and mathematical Sci., Vol. 24, No 7, pp. 433-435, 2000. |

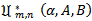 and
and 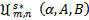 of normalized analytic functions in the open unit disk
of normalized analytic functions in the open unit disk 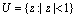 are investigated when
are investigated when 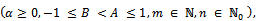 and several subordinations are obtained. A number of interesting consequences of these subordination results are also discussed.
and several subordinations are obtained. A number of interesting consequences of these subordination results are also discussed.
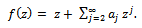
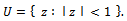 Shu-Hai and Tang in 2010[1], introduced the classes
Shu-Hai and Tang in 2010[1], introduced the classes 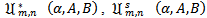 and gave the following definition:Definition 1. Let
and gave the following definition:Definition 1. Let 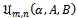 denote the subclass of
denote the subclass of 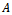 consisting of functions
consisting of functions 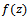 which satisfy the following inequality:
which satisfy the following inequality: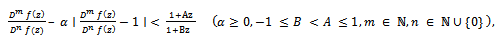
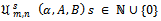 be the subclass of
be the subclass of 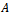 consisting of function
consisting of function 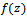 which satisfy the following condition:
which satisfy the following condition: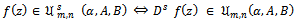
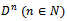 is the Salagean derivative operator defined as:
is the Salagean derivative operator defined as: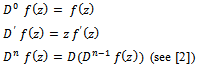 For
For 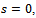 it is easy to see that
it is easy to see that 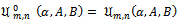 We denote by k the class of convex functions i.e.
We denote by k the class of convex functions i.e.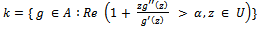 Definition 3. (Hadamard product or convolution) Given two functions
Definition 3. (Hadamard product or convolution) Given two functions 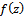 and
and 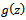 where
where 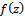 is as defined in (1.1) and
is as defined in (1.1) and 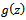 is given by
is given by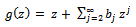
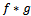 of
of 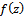 and
and 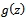 is defined by
is defined by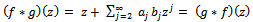
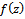 and
and 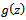 be analytic in the unit disk
be analytic in the unit disk 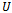 . Then
. Then 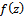 is said to be subordinate to
is said to be subordinate to 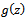 in
in 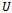 and we write
and we write 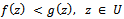 , if there exists a Schwarz function
, if there exists a Schwarz function 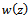 , analytic in
, analytic in 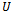 with
with 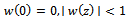 such that
such that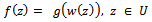
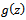 is univalent in
is univalent in 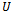 , then
, then 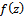 is subordinate to
is subordinate to 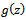 if
if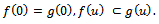
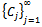 of complex numbers is said to be a subordinating factor sequence if whenever
of complex numbers is said to be a subordinating factor sequence if whenever 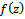 of the form (1.1) is analytic, univalent and convex in
of the form (1.1) is analytic, univalent and convex in 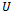 , the subordination is given by
, the subordination is given by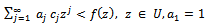 We have the following theoremTheorem 1.1 (Wilf [3])The sequence
We have the following theoremTheorem 1.1 (Wilf [3])The sequence 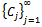 is a subordinating factor sequence if and only if
is a subordinating factor sequence if and only if 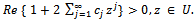
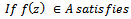
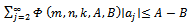
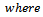
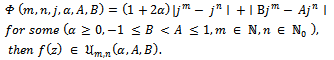
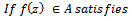
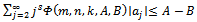
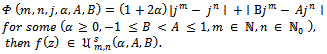
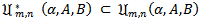 and
and 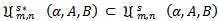 which consist of functions
which consist of functions 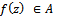 whose Taylor-Maclaurin coefficients
whose Taylor-Maclaurin coefficients 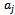 satisfy the inequalities (1.9) and (1.11) respectively.In our proposed investigation of functions in the classes
satisfy the inequalities (1.9) and (1.11) respectively.In our proposed investigation of functions in the classes 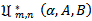 and
and 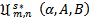 we obtain sharp subordination results for these classes and also investigate some applications of the main results which give important results of analytic functions.
we obtain sharp subordination results for these classes and also investigate some applications of the main results which give important results of analytic functions.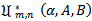 Theorem 2.1. Let
Theorem 2.1. Let 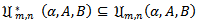
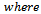
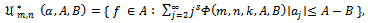
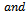
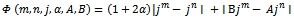
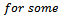
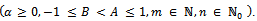
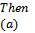
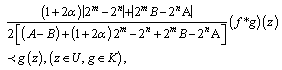
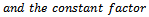
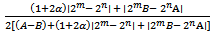
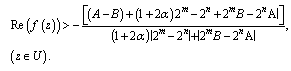
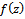 defined by (1.1) be any member of the class
defined by (1.1) be any member of the class 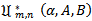 and suppose that
and suppose that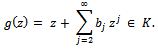 Then
Then 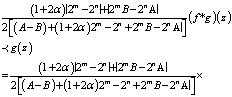
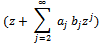 Thus, by Definition 5 the subordination (2.2) will hold if the sequence,
Thus, by Definition 5 the subordination (2.2) will hold if the sequence,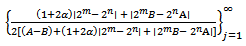
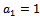 .Therefore by Theorem 1.1, it is sufficient to show that
.Therefore by Theorem 1.1, it is sufficient to show that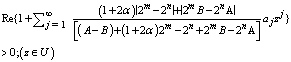
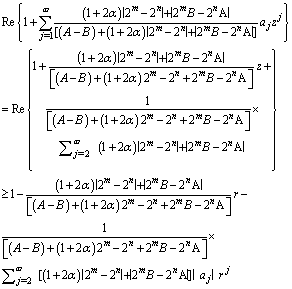
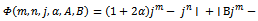 is an increasing function of
is an increasing function of  Thus,
Thus,
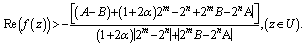 Now taking
Now taking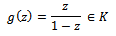 and
and 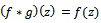 in (2.2) we have that
in (2.2) we have that 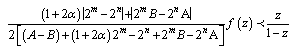
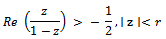
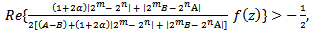
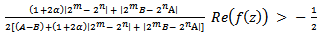
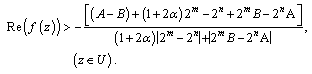 For
For 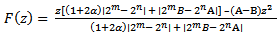
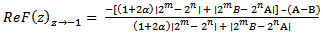
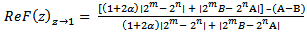
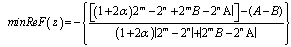
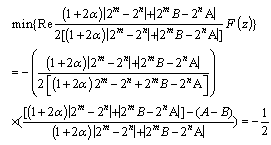
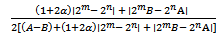 is the best possible and thus complete the proof of theorem 2.1.Subordination result for the class
is the best possible and thus complete the proof of theorem 2.1.Subordination result for the class 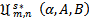 Our proof of Theorem 2.2 below is much akin to that of Theorem 2.1. Here we make use of Theorem 1.3 in place of Theorem 1.2 and let
Our proof of Theorem 2.2 below is much akin to that of Theorem 2.1. Here we make use of Theorem 1.3 in place of Theorem 1.2 and let 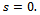 Theorem 2.2. Let
Theorem 2.2. Let 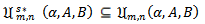
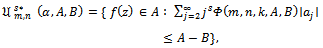
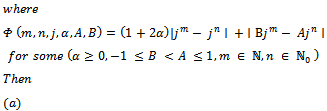
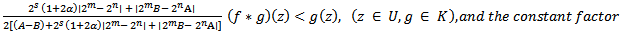
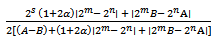
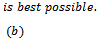
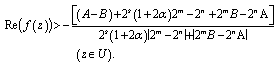
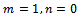 in Theorem 2.1; we obtain the following:Corollary1.
in Theorem 2.1; we obtain the following:Corollary1. 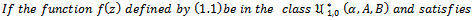
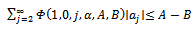
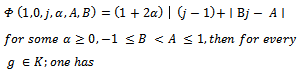
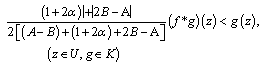
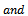
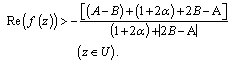
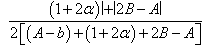
 Remark 1:
Remark 1: and Karthikenyan[5], and singh[6]
and Karthikenyan[5], and singh[6] Corollary2.
Corollary2. 
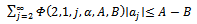
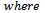
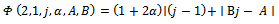
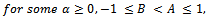
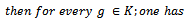
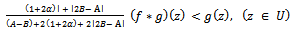
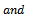
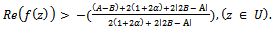
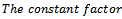
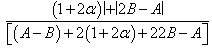
 Remark 2:The case
Remark 2:The case 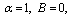 and
and 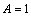 was obtained by Frasin [4], and Selvaraj and Karthikeyan [5].and Karthikeyan [5]
was obtained by Frasin [4], and Selvaraj and Karthikeyan [5].and Karthikeyan [5]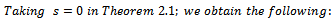
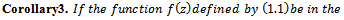
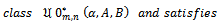
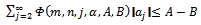
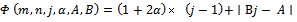
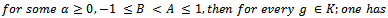
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML