Olanrewaju I. Shittu, Kazeem A. Adepoju
Department of Statistics, University of Ibadan, Ibadan, Nigeria
Correspondence to: Kazeem A. Adepoju, Department of Statistics, University of Ibadan, Ibadan, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, an optimal estimator for estimating the population mean is proposed. This is achieved by minimizing the coefficient of variation (Cx) of the auxiliary variable in the Mean Square Error (MSE) from the existing estimators. Using well analyzed data to illustrate the procedure for both the Ratio and Product estimators, a minimum of 10 percent reduction in the MSE were observed from each of the existing estimators considered. The proposed optimal estimators is uniformly better than all other estimators and thus most preferred over the existing modified ratio and product estimators for the use in practical applications for certain population with peculiar characteristics
Keywords:
Ratio, Product, Estimator, Parameter, Mean Square Error
Cite this paper: Olanrewaju I. Shittu, Kazeem A. Adepoju, On the Efficiency of Some Modified Ratio and Product Estimators – The Optimal Cx Approach, American Journal of Mathematics and Statistics, Vol. 3 No. 5, 2013, pp. 296-299. doi: 10.5923/j.ajms.20130305.07.
1. Introduction
Ratio estimation involves the use of known population totals for auxiliary variables to improve the weighting from sample values to population estimates of interest. It operates by comparing the sample estimate for an auxiliary variable with the known population total for the same variable on the frame. The ratio of the sample estimate of the auxiliary variable to its population total on the frame is used to adjust the sample estimate for the variable of interest. The ratio weights are given by Xx (where X is the known population total for the auxiliary variable and x is the corresponding estimate of the total based on all responding units in the sample). These weights assume that the population for the variable of interest will be estimated by the sample equally as well (or poorly) as the population total for the auxiliary variable is estimated by the sample.Consider a finite population U = {U1, U2, ….UN}of N distinct and identifiable units. Let Y be a study variable with value Yi measured on Ui, i = 1, 2, 3,………., N giving a vector Y= {Y1, Y2…, YN}. The problem is to estimate the population mean 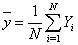 with some desirable properties on the basis of a random sample selected from the population U. The simplest estimator of population mean is the sample mean obtained by using simple random sampling without replacement, when there is no additional information on the auxiliary variable available. Sometimes in sample surveys, along with the study variable Y, information on auxiliary variable x correlated with Y is also collected. This information on auxiliary variable x, may be utilized to obtain a more efficient estimator of the population mean. The two broad categories of estimators using auxiliary information are the ratio method and product method of estimation. Among those who have worked on these estimators are Sisodia and Dwivedi[12], Pandey and Dubey[7], Singh, Taylor[10], Adewara and Singh[2]. The study is motivated by the success recorded by J. Subramani and G. Kumarapandiyan[8] on their respective works on “Modified ratio estimators using known median and coefficient of Kurtosis” and “Efficiency of some modified ratio and product Estimators using known value of some population parameters”.This work is focused on improving the efficiency of some Ratio and Product estimators in the literature by obtaining the optimal values of coefficient of variation of the auxiliary variable Cx in the MSE and then substitute back with some re-arrangement to obtain an improved estimate of the estimator and their respective MSE.
with some desirable properties on the basis of a random sample selected from the population U. The simplest estimator of population mean is the sample mean obtained by using simple random sampling without replacement, when there is no additional information on the auxiliary variable available. Sometimes in sample surveys, along with the study variable Y, information on auxiliary variable x correlated with Y is also collected. This information on auxiliary variable x, may be utilized to obtain a more efficient estimator of the population mean. The two broad categories of estimators using auxiliary information are the ratio method and product method of estimation. Among those who have worked on these estimators are Sisodia and Dwivedi[12], Pandey and Dubey[7], Singh, Taylor[10], Adewara and Singh[2]. The study is motivated by the success recorded by J. Subramani and G. Kumarapandiyan[8] on their respective works on “Modified ratio estimators using known median and coefficient of Kurtosis” and “Efficiency of some modified ratio and product Estimators using known value of some population parameters”.This work is focused on improving the efficiency of some Ratio and Product estimators in the literature by obtaining the optimal values of coefficient of variation of the auxiliary variable Cx in the MSE and then substitute back with some re-arrangement to obtain an improved estimate of the estimator and their respective MSE.
2. Literature Review
Sen., A.R.[9] presented an historical development of the ratio method of estimation starting from the year 1662. Auxiliary information is any information closely related to the study variable. The use of auxiliary information usually leads to the sampling strategy with higher efficiency compared to those in which no auxiliary information is used. Higher precision can also be achieved by using the auxiliary information for the dual purposes of selection and the estimation procedure. It is important to note that proper use of the knowledge of auxiliary information may result in appreciable gain in precision of the estimates. But indiscriminate use of auxiliary information might not provide the desired precision and in some extreme cases might even lead to loss in precision. Many authors since the discovery of ratio method of estimation have come up with various degree of modification of the conventional ratio estimations for better performance. These among others include Sisodia and Dwivedi[12], Singh and Tailor[10], Pandey and Dubey[7], Adewara and Singh[10] among others.
3. Methodology
3.1. Existing Modified Ratio and Product Estimators
Suppose a pairs (x, y) (i=1, 2, ….., n) observations are taken on n units sampled form N population units using simple random sampling without replacement scheme, 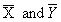 are the population means for the auxiliary variable (x) and variable of interest (y) and
are the population means for the auxiliary variable (x) and variable of interest (y) and 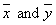 are the sample means based on the sample drawn. Khoshnevison et al[5] defined their family of estimators as:
are the sample means based on the sample drawn. Khoshnevison et al[5] defined their family of estimators as: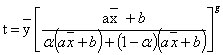 where
where 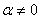 , b are either real numbers or a functions of the known parameters of the auxiliary variable x such as standard derivation
, b are either real numbers or a functions of the known parameters of the auxiliary variable x such as standard derivation 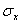 , coefficient of variation, Cx, Skewness
, coefficient of variation, Cx, Skewness  , Kurtosis
, Kurtosis 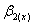 and correlation coefficient ρ.i. When α=1 a=1, b= 0, g=0, we have the usual ratio estimator,
and correlation coefficient ρ.i. When α=1 a=1, b= 0, g=0, we have the usual ratio estimator, 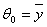 with
with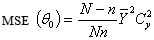 | (3.1) |
ii. When α=0 a=1, b= 0, g=1, we have the usual ratio estimator, 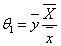 with
with 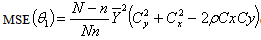 | (3.2) |
iii. When α=1 a=1, b= 0, g=-1, we have the usual product estimator, 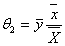 with
with 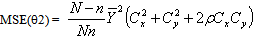 | (3.3) |
iv. When α=1 a=1, b= Cx, g=1, Sisodia and Dwivedi[12] ratio estimator  with
with 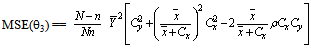 | (3.4) |
v. When α=1 a=1, b=Cx, g=1, we have Pandey and Dubey[7] product estimator with 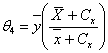 with
with  | (3.5) |
vi. When α=1 a=1, b=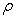 , g=1, we have Singh, Taylor[10] ratio estimator as
, g=1, we have Singh, Taylor[10] ratio estimator as 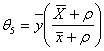 with
with 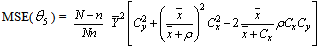 | (3.6) |
vii. When α=1 a=-1, b=ρ ,g=1, we have Singh, Taylor[10] product estimator 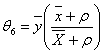 with
with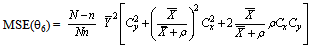 | (3.7) |
It should be noted that there are other ratio and product estimators from the family mentioned above, but here attention is focused on those estimators that uses the coefficient of variation Cx and correlation coefficient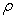 . Conventionally, for ratio estimators to hold,
. Conventionally, for ratio estimators to hold, 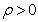 and also for product estimators to hold,
and also for product estimators to hold, 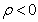 .
.
3.2. Proposed Ratio and Product Estimators
The proposed optimal estimators were obtained by minimizing the MSE(.) from each of the existing estimators with respect to Cx and equate to zero. The solution for Cx is then substituted back to initial MSE(.) to get the modified optimal estimators and corresponding MSE(*.) as follows in equations 3.8 to 3.12 below: i. 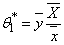
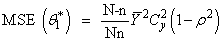 | (3.8) |
ii. 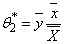
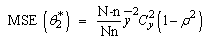 | (3.9) |
iii. 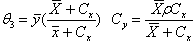
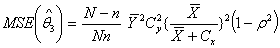 | (3.10) |
iv. 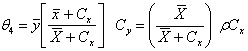
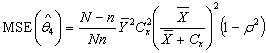 v.
v. 
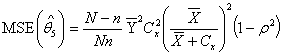 | (3.11) |
vi.
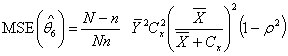 | (3.12) |
3.3. Data Used
Following Adewara et. al.[2], data sets from two populations are used:Population I: Kadilar and Cingi1[3] with the parameters: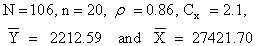 Population II: Maddala (1977) with the parameters:
Population II: Maddala (1977) with the parameters: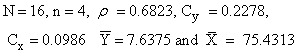 Since conventionally, for ratio estimators to hold,
Since conventionally, for ratio estimators to hold,  and also for product estimators to hold,
and also for product estimators to hold, 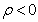 .
.
4. Results and Discussions
The results obtained from the application of the two data sets to the Mean square error of the conventional and proposed ratio and product estimators in equations 3.8 to 3.12 are shown tables 1 and 2 below:It can be observed from table 1 that the MSE for the proposed estimators are less that each of the existing ratio estimators. Also it can be observed from table 2 that the MSE for the proposed estimators are less that each of the existing product estimators.Table 1. Mean Square Errors (MSE) of the estimates of Existing and Proposed Estimators (Ratio Estimators) with Population I
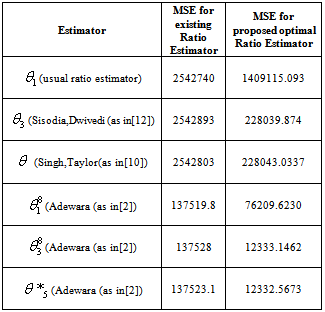 |
| |
|
Table 2. Mean Square Errors (MSE) of the estimates of Existing and Proposed Estimators (Product Estimators) with Population II
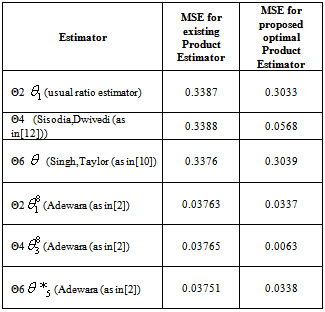 |
| |
|
5. Conclusions
In this study, we have proposed an optimal estimators for the ratio estimators and product estimators by minimizing the coefficient of variation of the auxiliary variable x. Using the Kadilar and Cingi1[3] and Maddala[6] data for the proposed estimators, a gain of a least 10% precision was achieved over the existing estimators for both the ratio and product estimators in the literature. Therefore, the proposed optimal estimators is uniformly better than all other estimators and thus most preferred over the existing modified ratio and product estimators for the use in practical applications for certain population with peculiar characteristics.
References
| [1] | Adewara, A.A. (2006): Effects of improving both the auxiliary and variable of interest in ratio and product estimators. Proc. Pakistan Acad. Sci. 43(4): 275-278. |
| [2] | Adewara, A.A, Rajesh S and Mukesh Kumar (2012): “Efficiency of some Modified Ratio and Product Estimators Using Known Values of Some Population Parameters” Intl. Jour. Of Applied sciences and Technology, Vol. 2 (2) Pgs. 76 -79. |
| [3] | Kadilar, C. and Cingi, H. (2004). Ratio Estimators in Simple Random Sampling. Appl. Mathe. and Comput. 151, 893-902. |
| [4] | Kadilar, C. and Cingi, H. (2006): Ratio estimators for the population variance in sample and stratified random sampling. Appl. Mathe. and Comput. 173, 1047-1059. |
| [5] | Khoshnevisan, M., Singh, R., Chauhan, P., Sawan, N. and Smarandache, F. (2007): A general family of estimators for estimating population mean using known value of population parameter(s). For East Jour. of theor. Statist. 22(2), 181-191. |
| [6] | Maddala, G.S. (1977): Econometrics. “McGraw Hills Pub. Co.” New York. |
| [7] | Pandey, B.N. and Dubey, Vyas (1988): Modified product estimator using coefficient of variation of auxiliary variate, Assam Statistical Rev., 2(2), 64 – 66. |
| [8] | Subramani, J. and Kumarapandiyan, G. (2012). Modified Ratio Estimator for Population Mean Using Median of the Auxiliary Variable, Proceedings of National Conference on Recent developments in the Applications of Reliability Theory and Survival Analysis held on 2nd and 3rd February 2012 at the Department of Statistics, Pondicherry University |
| [9] | Sen, A.R. (1993): Some early developments in ratio estimation, Biometric Journal 35(1), 3 13 |
| [10] | Singh, H.P. and Tailor, R. (2003): Use of known correlation coefficient in estimating the finite population mean. Statist. in Trans 6(4). 555-560. |
| [11] | Srivenkataramana, T. and Srinath, K.P. (1976): Ratio and Product methods of estimation in sample surveys when the two variables are moderately correlated. Vignana Bharathi 2:54-58. |
| [12] | Sisodia, B.V.S and Dwivedi, V.K. (1981): A modified ratio estimator using coefficient of variation of auxiliary variable. Journal Ind. Soc. Agril. Statist., 33(2), 13-18 . |
| [13] | Yan, Z. and Tian, B. (2010). Ratio Method to the Mean Estimation Using Co-efficient of Skewness of Auxiliary Variable, ICICA 2010, Part II, CCIS 106, pp. 103–110 |

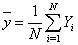 with some desirable properties on the basis of a random sample selected from the population U. The simplest estimator of population mean is the sample mean obtained by using simple random sampling without replacement, when there is no additional information on the auxiliary variable available. Sometimes in sample surveys, along with the study variable Y, information on auxiliary variable x correlated with Y is also collected. This information on auxiliary variable x, may be utilized to obtain a more efficient estimator of the population mean. The two broad categories of estimators using auxiliary information are the ratio method and product method of estimation. Among those who have worked on these estimators are Sisodia and Dwivedi[12], Pandey and Dubey[7], Singh, Taylor[10], Adewara and Singh[2]. The study is motivated by the success recorded by J. Subramani and G. Kumarapandiyan[8] on their respective works on “Modified ratio estimators using known median and coefficient of Kurtosis” and “Efficiency of some modified ratio and product Estimators using known value of some population parameters”.This work is focused on improving the efficiency of some Ratio and Product estimators in the literature by obtaining the optimal values of coefficient of variation of the auxiliary variable Cx in the MSE and then substitute back with some re-arrangement to obtain an improved estimate of the estimator and their respective MSE.
with some desirable properties on the basis of a random sample selected from the population U. The simplest estimator of population mean is the sample mean obtained by using simple random sampling without replacement, when there is no additional information on the auxiliary variable available. Sometimes in sample surveys, along with the study variable Y, information on auxiliary variable x correlated with Y is also collected. This information on auxiliary variable x, may be utilized to obtain a more efficient estimator of the population mean. The two broad categories of estimators using auxiliary information are the ratio method and product method of estimation. Among those who have worked on these estimators are Sisodia and Dwivedi[12], Pandey and Dubey[7], Singh, Taylor[10], Adewara and Singh[2]. The study is motivated by the success recorded by J. Subramani and G. Kumarapandiyan[8] on their respective works on “Modified ratio estimators using known median and coefficient of Kurtosis” and “Efficiency of some modified ratio and product Estimators using known value of some population parameters”.This work is focused on improving the efficiency of some Ratio and Product estimators in the literature by obtaining the optimal values of coefficient of variation of the auxiliary variable Cx in the MSE and then substitute back with some re-arrangement to obtain an improved estimate of the estimator and their respective MSE.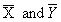 are the population means for the auxiliary variable (x) and variable of interest (y) and
are the population means for the auxiliary variable (x) and variable of interest (y) and 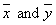 are the sample means based on the sample drawn. Khoshnevison et al[5] defined their family of estimators as:
are the sample means based on the sample drawn. Khoshnevison et al[5] defined their family of estimators as: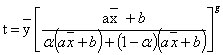 where
where 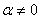 , b are either real numbers or a functions of the known parameters of the auxiliary variable x such as standard derivation
, b are either real numbers or a functions of the known parameters of the auxiliary variable x such as standard derivation 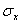 , coefficient of variation, Cx, Skewness
, coefficient of variation, Cx, Skewness  , Kurtosis
, Kurtosis 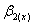 and correlation coefficient ρ.i. When α=1 a=1, b= 0, g=0, we have the usual ratio estimator,
and correlation coefficient ρ.i. When α=1 a=1, b= 0, g=0, we have the usual ratio estimator, 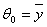 with
with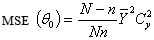
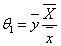 with
with 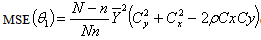
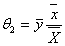 with
with 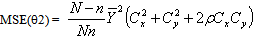
 with
with 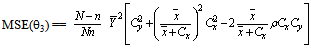
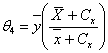 with
with 
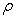 , g=1, we have Singh, Taylor[10] ratio estimator as
, g=1, we have Singh, Taylor[10] ratio estimator as 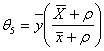 with
with 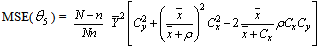
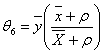 with
with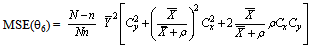
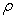 . Conventionally, for ratio estimators to hold,
. Conventionally, for ratio estimators to hold, 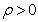 and also for product estimators to hold,
and also for product estimators to hold, 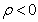 .
.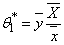
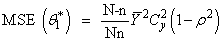
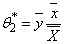
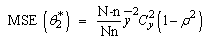
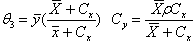
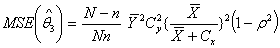
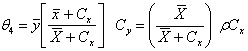
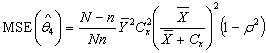 v.
v. 
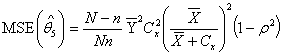

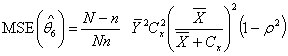
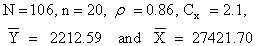 Population II: Maddala (1977) with the parameters:
Population II: Maddala (1977) with the parameters: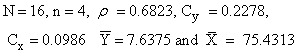 Since conventionally, for ratio estimators to hold,
Since conventionally, for ratio estimators to hold,  and also for product estimators to hold,
and also for product estimators to hold, 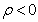 .
. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
