-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(5): 288-295
doi:10.5923/j.ajms.20130305.06
Estimation of Allele and Extinction Probability from Generations of an Ancestor
Babulal Seal
Department of Statistics, Burdwan University, Burdwan, W.B., India
Correspondence to: Babulal Seal, Department of Statistics, Burdwan University, Burdwan, W.B., India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In population genetics estimation of alleles for a gene is important to understand the character of the population. Several works are available in the literature and these are based on gene-type data of a population. They collect data from several units. But they do not collect data of an unit from the generations for estimating this. Considering the variation of genes from the generations of an unit, an estimation procedure of di-allele is attempted. Though it started from an unit, this method can be extended for many units also. However, variations over generations are considered and with this kind of data-format the extinction probability is estimated which is logical as variations of gene along generations are important. These estimates of di-alleles have been computed. Also the performance of estimators based on three generations and four generations are compared. As expected from common sense, it is seen in findings also that if one takes data from more generations then estimator becomes improved. For comparing these risks using three generations and four generations were computed and plotted. Along this line the work can be generalized by considering many units and more generations.
Keywords: Branching Process, Probability Generating Function, m. l. e.
Cite this paper: Babulal Seal, Estimation of Allele and Extinction Probability from Generations of an Ancestor, American Journal of Mathematics and Statistics, Vol. 3 No. 5, 2013, pp. 288-295. doi: 10.5923/j.ajms.20130305.06.
Article Outline
1. Introduction
- Extinction probability[1] of a gene and its estimation[2] is important to understand whether a character will be vanished in the long run or not. Being motivated while working with estimation of extinction probability, it is found that the technique may be used for estimating allele also. For this we may use observations from a population or may use data from the generation chain of a single unit.In population genetics estimation of alleles for a gene is important to understand the character of the population. Several works are available in the literature eg[3] these are based on gene-type data of the population. They collect data from several units. But they do not use data of an unit from the generations for estimating this. Considering the variation of genes from the generations of an unit, an estimation procedure of di-allele is attempted. In fact this is a kind of branching process[4]&[5]. Estimation of some branching processes are discussed in[6] &[7]. In section 2, estimation from three generation data is given by using m.l.e. Here estimation of
 , proportion of allele ‘a’ is given and
, proportion of allele ‘a’ is given and 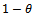 is proportion of allele ‘A’. For simplicity we may pretend that a unit gives birth at most two offspring having
is proportion of allele ‘A’. For simplicity we may pretend that a unit gives birth at most two offspring having 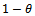 = probability of being male. In that section using one unit, the estimates are given and estimation of extinction probability is also given. The risk function[8] is also calculated. In section 3 same things are carried out using four generation data. This is for simple type of branching process as described. There are many types of branching processes also e.g.[9]. In section 4 two risk functions are obtained from results of section 2 and section 3 graphically by using R- program and using squared error loss function. It is found that the second one is better for most of
= probability of being male. In that section using one unit, the estimates are given and estimation of extinction probability is also given. The risk function[8] is also calculated. In section 3 same things are carried out using four generation data. This is for simple type of branching process as described. There are many types of branching processes also e.g.[9]. In section 4 two risk functions are obtained from results of section 2 and section 3 graphically by using R- program and using squared error loss function. It is found that the second one is better for most of 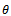 values. This is logical because more generations give the true reflection of the allele as was partially thought. It is believed that if we use more generations then estimate of
values. This is logical because more generations give the true reflection of the allele as was partially thought. It is believed that if we use more generations then estimate of 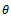 value will improve. However, that is a point of more investigations. But up to these generations it seems to be consistent.The reason that first one is slightly better for
value will improve. However, that is a point of more investigations. But up to these generations it seems to be consistent.The reason that first one is slightly better for 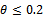 may be the following. Small
may be the following. Small 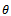 implies more ‘males’ but using more generations implies variation among data set i.e., mixing of ‘male’, ‘female’ information contradict that truly there are only ‘males’.
implies more ‘males’ but using more generations implies variation among data set i.e., mixing of ‘male’, ‘female’ information contradict that truly there are only ‘males’.2. Method for Estimation of Probability of Extinction
- Suppose we want to make inference about branching process using data over generations. Let the generations be
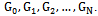 We consider the simple case where a particle gives birth at most 2 offspring as
We consider the simple case where a particle gives birth at most 2 offspring as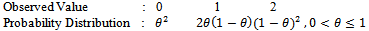 Now at
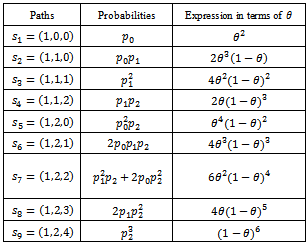
Now at  if one stars with one unit, then in the following all possible paths through the three generations may be observed. In the following, possible sample values together with transition probabilities inside the 1st bracket are given for each generation (column-wise).
if one stars with one unit, then in the following all possible paths through the three generations may be observed. In the following, possible sample values together with transition probabilities inside the 1st bracket are given for each generation (column-wise).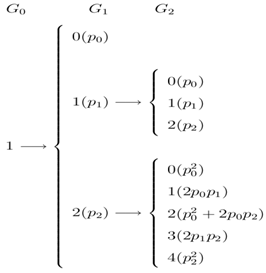 It is to be noted that the probability generating function (p.g.f.) from a single unit is
It is to be noted that the probability generating function (p.g.f.) from a single unit is 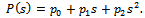 The p.g.f. obtain from two units X, Y will be
The p.g.f. obtain from two units X, Y will be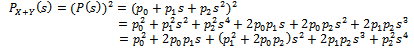 So the possible paths together with probabilities will be:
So the possible paths together with probabilities will be:
|
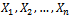 i.i.d observations from the above distribution. Then the joint density becomes
i.i.d observations from the above distribution. Then the joint density becomes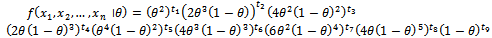 where
where 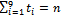 and ti=number of si sample for i=1,2,…,9Therefore
and ti=number of si sample for i=1,2,…,9Therefore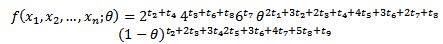 In order to obtain maximum likelihood estimate
In order to obtain maximum likelihood estimate 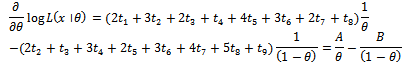 where
where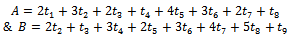 Now
Now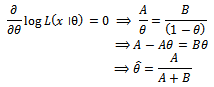
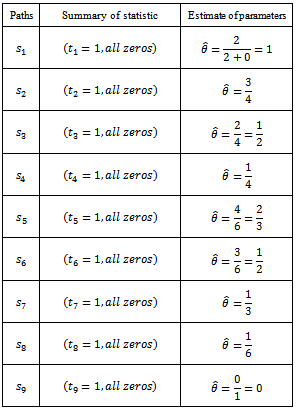
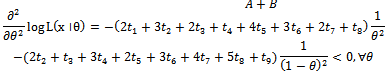 Hence above estimate is a maximum likelihood estimate.Now based on one sample path the estimates are as follows:
Hence above estimate is a maximum likelihood estimate.Now based on one sample path the estimates are as follows:
|
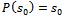
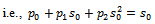
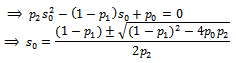 where
where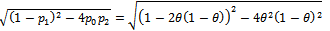
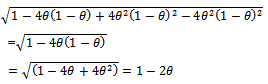 Therefore,
Therefore,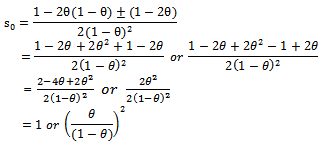 So the extinction probability is
So the extinction probability is 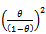 & it’s estimate will be
& it’s estimate will be 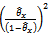 where
where 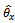 are given in (2.1).Remark 2.1It is to be noted that
are given in (2.1).Remark 2.1It is to be noted that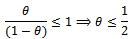 Now let us choose
Now let us choose 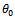 be such that
be such that  then
then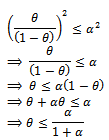 So if
So if 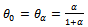 then
then 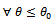 we have
we have 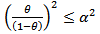 as
as 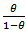 is an
is an  function of
function of 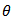 If we collect huge data and obviously this is not a difficult task, then from each subset of data one can obtain estimates. From several such estimate one can find the prior distribution of θ and if it is seen that it has negligible weights beyond
If we collect huge data and obviously this is not a difficult task, then from each subset of data one can obtain estimates. From several such estimate one can find the prior distribution of θ and if it is seen that it has negligible weights beyond 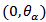 then there is nothing to be worried about of being extinct.Remark 2.2Actually θ is controlled by the sex gene factor and from one generation we can not get good information about that. For this we should read pattern of transition from one generation to another. But for practical purposes we may not get data for many generations. But at least using 3 or 4 generations we should study the transitions.Remark 2.3Above can be used in testing the hypothesis regarding the sex gene i.e.
then there is nothing to be worried about of being extinct.Remark 2.2Actually θ is controlled by the sex gene factor and from one generation we can not get good information about that. For this we should read pattern of transition from one generation to another. But for practical purposes we may not get data for many generations. But at least using 3 or 4 generations we should study the transitions.Remark 2.3Above can be used in testing the hypothesis regarding the sex gene i.e. 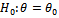 or one can get idea whether two communities have equal θ‘s through usual Neyman Pearson test. Before doing that we are to compute its statistical curvature as the above family is a curved exponential family. We can say that tests of curved family holds good if its statistical curvature is small i.e., it does not deviate from regular 2-parameter exponential family much.
or one can get idea whether two communities have equal θ‘s through usual Neyman Pearson test. Before doing that we are to compute its statistical curvature as the above family is a curved exponential family. We can say that tests of curved family holds good if its statistical curvature is small i.e., it does not deviate from regular 2-parameter exponential family much.3. General Case
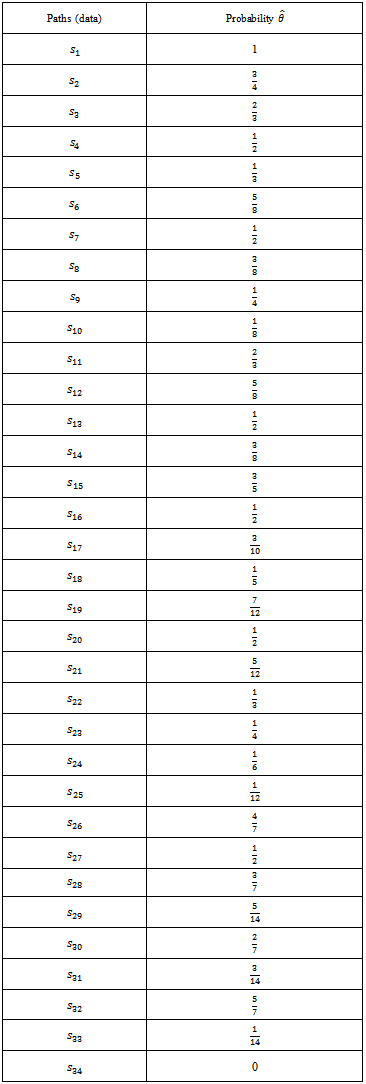
- Now depending on the lengths of chain let us see the behavior of the estimator and compare this case with previous one via MSEIf we take four generation then the sample paths, probabilities will be as in the following.
|
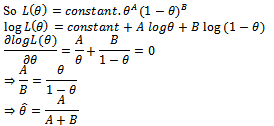 Estimator of the parameter using above paths
Estimator of the parameter using above paths
|
4. Comparison of Two Estimators Using 3 Generations and 4 Generations
- R-codes for computations of the risk functions and plotting of the risk functions.

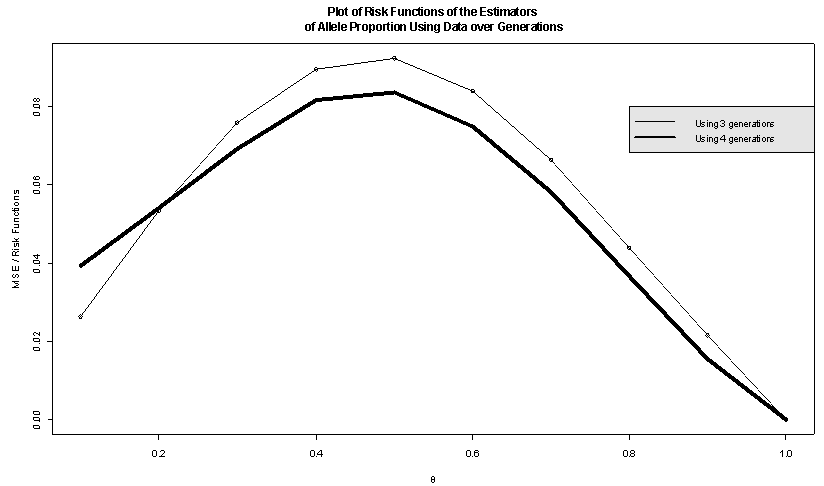 | Figure 1. Comparison of two risk function |
5. Concluding Remarks
- There are enough scopes for elaborating the inference part like observing samples with more generations. The testing part in this regard should be carefully handled, as the family distribution here is a curved exponential family.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML