| [1] | Lord, F. M., 1952, A theory of test scores, Psychometric Monograph No. 7. |
| [2] | Lord, F. M., and Novick, M. R., 1968, Statistical theories of mental test scores, Addison-Wesley, Reading, MA. |
| [3] | Lord, F. M., 1980, Applications of item response theory to practical testing problems, Lawrence Erlbaum Associates, Hillsdale, New Jersey. |
| [4] | Smith, A. F. M., and Roberts, G. O., 1993, Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods, Journal of the Royal Statistical Society, Series B, 55, 3–23. |
| [5] | Tierney, L., 1994, Markov chains for exploring posterior distributions, The Annals of Statistics, 22, 1701–1762. |
| [6] | Carlin, B. P., and Louis, T. A., 2000, Bayes and empirical Bayes methods for data analysis (2nd ed.), Chapman & Hall, London. |
| [7] | Chib, S., and Greenberg, E., 1995, Understanding the Metropolis-Hastings algorithm, The American Statistician, 49(4), 327–335. |
| [8] | Gelfand, A. E., and Smith, A. F. M., 1990, Sampling-based approaches to calculating marginal densities, Journal of the American Statistical Association, 85, 398–409. |
| [9] | Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B., 2003, Bayesian data analysis, Chapman & Hall/CRC, Boca Raton. |
| [10] | Albert, J. H., 1992, Bayesian estimation of normal ogive item response curves using Gibbs sampling, Journal of Educational Statistics, 17, 251–269. |
| [11] | Geman, S., and Geman, D., 1984, Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images, IEEE Trans. Pattern Analysis and Machine Intelligence, 6, 721–741. |
| [12] | Tanner, M. A., and Wong, W. H., 1987, The calculation of posterior distribution by data augmentation (with discussion), Journal of the American Statistical Association, 82, 528–550. |
| [13] | Sheng, Y., and Headrick, T. C., 2007, An algorithm for implementing Gibbs sampling for 2PNO IRT models, Journal of Modern Applied Statistical Methods, 6, 341–349. |
| [14] | Sahu, S. K., 2002, Bayesian estimation and model choice in item response models, Journal of Statistical Computation and Simulation, 72, 217–232. |
| [15] | Johnson, V. E., and Albert, J. H., 1999, Ordinal data modeling, Springer-Verlag, New York. |
| [16] | Béguin, A. A., and Glas, C. A. W., 2001, MCMC estimation and some model-fit analysis of multidimensional IRT models, Psychometrika, 66, 541–562. |
| [17] | Glas, C. W., and Meijer, R. R., 2003, A Bayesian approach to person fit analysis in item response theory models, Applied Psychological Measurement, 27, 217–233. |
| [18] | Sheng, Y., 2008, Markov chain Monte Carlo estimation of normal ogive IRT models in MATLAB, Journal of Statistical Software, 25(8), 1–15. |
| [19] | Sheng, Y., 2010, A sensitivity analysis of Gibbs sampling for 3PNO IRT models: Effects of prior specifications on parameter estimates, Behaviormetrika, 37(2), 87–110. |
| [20] | Sheng, Y., 2013, An empirical investigation of Bayesian hierarchical modeling with unidimensional IRT models, Behaviormetrika, 40(1), 19–40. |
| [21] | Williams, C. L., and Locke, A., 2003, Hyperprior imprecision in hierarchical Bayesian modeling of cluster Bernoulli observations, InterStat: Statistics on the Internet. URL: http://interstat.statjournals.net/YEAR/2003/abstracts/0310001.php. |
| [22] | Brainerd, W., 2003, The importance of Fortran in the 21st century, Journal of Modern Statistical Methods, 2, 14–15. |
| [23] | Patz, R. J., and Junker, B. W., 1999, A straightforward approach to Markov chain Monte Carlo methods for item response models, Journal of Educational and Behavioral Statistics, 24, 146–178. |
| [24] | Ripley, B. D., 1987, Stochastic simulation, Wiley, New York. |
| [25] | Gelfand, A. E., Hills, S. E., Racine-Poon, A., and Smith, A. F. M., 1990, Illustration of Bayesian inference in normal data models using Gibbs sampling, Journal of the American Statistical Association, 85, 315–331. |
| [26] | Hoijtink, H., and Molenaar, I. W., 1997, A multidimensional item response model: Constrained latent class analysis using posterior predictive checks, Psychometrika, 62, 171–189. |

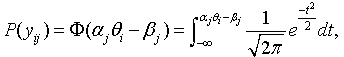
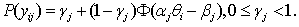
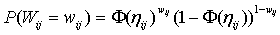
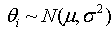 ,
, 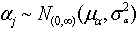 ,
, 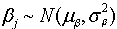 ,
,  . Note that we consider models where the prior distributions are assumed for the hyperparameters µα, µβ, σ2α and σ2β, instead of specifying values for them.The joint posterior distribution of (θ, ξ, γ, W, Z, µξ, ∑ξ), where ξj = (αj, βj)′, µξ =(µα, µβ)′, ∑ξ = diag(σ2α, σ2β), is
. Note that we consider models where the prior distributions are assumed for the hyperparameters µα, µβ, σ2α and σ2β, instead of specifying values for them.The joint posterior distribution of (θ, ξ, γ, W, Z, µξ, ∑ξ), where ξj = (αj, βj)′, µξ =(µα, µβ)′, ∑ξ = diag(σ2α, σ2β), is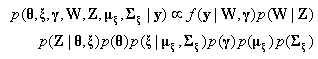
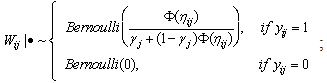

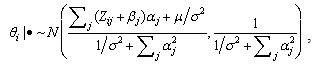
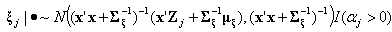
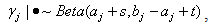
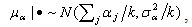
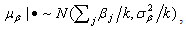
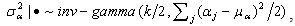

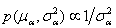 and
and 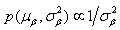 , or as
, or as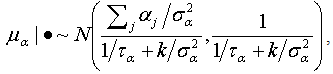
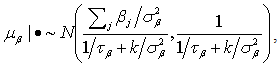
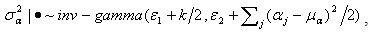
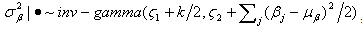
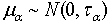 ,
,  ,
, 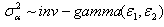 ,
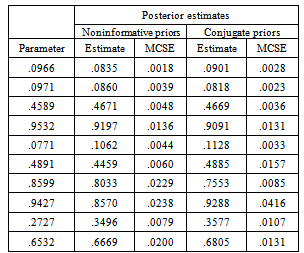
,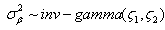 .As such, using starting values of θ(0), ξ(0), γ(0), µξ(0) and ∑ξ(0), observations (W(l), Z(l), θ(l), ξ(l), γ(l), µξ(l), ∑ξ(l)) can be simulated from the Gibbs sampler by iteratively drawing from their respective full conditional distributions specified in (5) through (15). The transition from (W(l–1), Z(l–1), θ(l –1), ξ(l–1), γ(l–1), µξ(l–1), ∑ξ(l–1)) to (W(l), Z(l), θ(l), ξ(l), γ(l), µξ(l), ∑ξ(l)) is based on the following seven steps:1. Draw W(l) ~ p(W|y, θ(l –1), ξ(l–1), γ(l–1));2. Draw Z(l) ~ p(Z|W(l), θ(l –1), ξ(l–1));3. Draw θ(l) ~ p(θ|Z(l), ξ(l–1));4. Draw ξ(l) ~ p(ξ|Z(l), θ(l), µξ(l–1), ∑ξ(l–1));5. Draw γ(l) ~ p(γ|y, W(l));6. Draw µξ(l) ~ p(µξ|ξ(l),∑ξ(l–1));7. Draw ∑ξ(l) ~ p(∑ξ|ξ(l), µξ(l)).This iterative procedure produces a sequence of (θ(l), ξ(l), γ(l)), l =1,…, L. To reduce the effect of the starting values, early iterations in the Markov chain are set as burn-ins to be discarded. Samples from the remaining iterations are then used to summarize the posterior density of the item parameters ξ, γ and person parameters θ. As with standard Monte Carlo, with large enough samples, the posterior means of ξ, γ and θ are considered as estimates of the true parameters. However, their Monte Carlo standard errors cannot be calculated using the sample standard deviations because subsequent samples in each Markov chain are autocorrelated (e.g.[10, 23]). One approach to calculating the standard errors is through batching[24]. Specifically, with a long chain of samples being separated into contiguous batches of equal length, the Monte Carlo standard deviation for each parameter is then estimated to be the standard deviation of these batched means. And the Monte Carlo standard error of the estimate is a ratio of the Monte Carlo standard deviation and the square root of the number of batches.
.As such, using starting values of θ(0), ξ(0), γ(0), µξ(0) and ∑ξ(0), observations (W(l), Z(l), θ(l), ξ(l), γ(l), µξ(l), ∑ξ(l)) can be simulated from the Gibbs sampler by iteratively drawing from their respective full conditional distributions specified in (5) through (15). The transition from (W(l–1), Z(l–1), θ(l –1), ξ(l–1), γ(l–1), µξ(l–1), ∑ξ(l–1)) to (W(l), Z(l), θ(l), ξ(l), γ(l), µξ(l), ∑ξ(l)) is based on the following seven steps:1. Draw W(l) ~ p(W|y, θ(l –1), ξ(l–1), γ(l–1));2. Draw Z(l) ~ p(Z|W(l), θ(l –1), ξ(l–1));3. Draw θ(l) ~ p(θ|Z(l), ξ(l–1));4. Draw ξ(l) ~ p(ξ|Z(l), θ(l), µξ(l–1), ∑ξ(l–1));5. Draw γ(l) ~ p(γ|y, W(l));6. Draw µξ(l) ~ p(µξ|ξ(l),∑ξ(l–1));7. Draw ∑ξ(l) ~ p(∑ξ|ξ(l), µξ(l)).This iterative procedure produces a sequence of (θ(l), ξ(l), γ(l)), l =1,…, L. To reduce the effect of the starting values, early iterations in the Markov chain are set as burn-ins to be discarded. Samples from the remaining iterations are then used to summarize the posterior density of the item parameters ξ, γ and person parameters θ. As with standard Monte Carlo, with large enough samples, the posterior means of ξ, γ and θ are considered as estimates of the true parameters. However, their Monte Carlo standard errors cannot be calculated using the sample standard deviations because subsequent samples in each Markov chain are autocorrelated (e.g.[10, 23]). One approach to calculating the standard errors is through batching[24]. Specifically, with a long chain of samples being separated into contiguous batches of equal length, the Monte Carlo standard deviation for each parameter is then estimated to be the standard deviation of these batched means. And the Monte Carlo standard error of the estimate is a ratio of the Monte Carlo standard deviation and the square root of the number of batches. 
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML