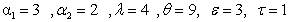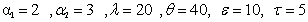Hamdy M. Salem
Department of Statistics, Faculty of Commerce, Al-Azher University, Egypt & Qassim University, Community College in Buraidah, Saudi Arabia
Correspondence to: Hamdy M. Salem, Department of Statistics, Faculty of Commerce, Al-Azher University, Egypt & Qassim University, Community College in Buraidah, Saudi Arabia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper deals with the estimation of the reliability  when
when  and
and  are independent variables distributed as Weighted Weibull Distribution. Different methods for estimating the reliability are obtained such as Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators which are based on non-informative and informative prior distributions. A comparison of the estimates obtained is performed as well. Finally a numerical investigation is carried out to study the properties of the new estimators.
are independent variables distributed as Weighted Weibull Distribution. Different methods for estimating the reliability are obtained such as Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators which are based on non-informative and informative prior distributions. A comparison of the estimates obtained is performed as well. Finally a numerical investigation is carried out to study the properties of the new estimators.
Keywords:
Reliability, Stress-Strength, Maximum Likelihood Estimator; Bayesian Estimator, Weighted Weibull Distributions
Cite this paper: Hamdy M. Salem, Inference on Stress-Strength Reliability for Weighted Weibull Distribution, American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 220-226. doi: 10.5923/j.ajms.20130304.06.
1. Introduction
It has become a fact that improving the quality of products depends mainly on the on going demand for these products. In addition, staying in the market has become also associated with the reliability of such products. For these reasons, companies need to meet specific measure to compete in world wide markets such as, its ability to high quality, competitive prices, and reliable goods on time. In thisregards, manufactures use formative assessment for there products to achieve reliability which is closely related to durability, accessibility and survival. Failure can beconsidered a random variable since it is so difficult to tell precisely when a specific product will fail under use condition.Under normal condition, measure of reliability for device becomes too difficult and it requires very long time. So, accelerated life testing induces failures and the failure data at the accelerated conditions are used to estimate the reliability at normal operating conditions when the reliability of a component is "high" and failure data of the component may not be attainable during its expected life. The problem of estimating the reliability  arises in the situation of mechanical reliability of a system with strength
arises in the situation of mechanical reliability of a system with strength 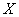 and stress
and stress 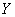 , and R is a determine of system reliability. The system fails if and only if, at any time the stress exceeds the strength.Many authors have measured different choices for stress and strength distributions. Johnson (1988)[10] summarized some of these choices. Awad & Gharraf (1986)[5] considered the case when
, and R is a determine of system reliability. The system fails if and only if, at any time the stress exceeds the strength.Many authors have measured different choices for stress and strength distributions. Johnson (1988)[10] summarized some of these choices. Awad & Gharraf (1986)[5] considered the case when  and
and 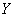 are independent and have Burr Type XII random variables. They obtained a maximum likelihood estimator, minimum variance unbiased estimator, and a Bayesian estimator for R. They used a numerical procedure for evaluating their Bayesian estimator. Alam & Roohi (2002)[3] studied stress and strength having exponential distribution but in (2003)[4] have studied the problem of
are independent and have Burr Type XII random variables. They obtained a maximum likelihood estimator, minimum variance unbiased estimator, and a Bayesian estimator for R. They used a numerical procedure for evaluating their Bayesian estimator. Alam & Roohi (2002)[3] studied stress and strength having exponential distribution but in (2003)[4] have studied the problem of 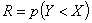 in a different way. They have set up the required parametric values of the assumed distributions as a replacement for finding P (YThe Weibull distribution is one of the most widely used distributions in the reliability and survival studies. Baklizi (2012)[7] considered the stress-strength reliability based on record values from the Weibull distribution. He obtained the Bayes estimator based on squared error loss and the maximum likelihood estimator of the reliability R. Akbar et al (2012) )[2] focus on the inference for the stress- strength reliability R when X and Y are two independent Weibull distributions with the same shape parameter, but having the different scale parameters. They obtained The maximum likelihood and the approximate maximum likelihood estimators of R. Azzalini (1985)[6] suggested a method of obtaining weighted distributions from independently identically distributed random variables. He used the density function of one random variable and the distribution function of the other random variable as follows:
in a different way. They have set up the required parametric values of the assumed distributions as a replacement for finding P (YThe Weibull distribution is one of the most widely used distributions in the reliability and survival studies. Baklizi (2012)[7] considered the stress-strength reliability based on record values from the Weibull distribution. He obtained the Bayes estimator based on squared error loss and the maximum likelihood estimator of the reliability R. Akbar et al (2012) )[2] focus on the inference for the stress- strength reliability R when X and Y are two independent Weibull distributions with the same shape parameter, but having the different scale parameters. They obtained The maximum likelihood and the approximate maximum likelihood estimators of R. Azzalini (1985)[6] suggested a method of obtaining weighted distributions from independently identically distributed random variables. He used the density function of one random variable and the distribution function of the other random variable as follows: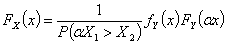 | (1.1) |
Recently, Gupta & Kundu, (2009)[9] presented a new class of weighted exponential distributions. Makhdoom (2012)[13] studied the estimation of Stress-Strength reliability when X and Y are two weighted exponential distributions with different parameters. He obtained the MLE of R based on one simple iteration procedure, and he carried out Bayesian estimators of parameters with real data. Saman et al. (2010)[15] proposed The weighted Weibull model based on an idea of Azzalini (1985)[6]. They studied basic properties of the distribution including moments, generating function, hazard rate function and estimation of parameters. The proposing model which in Saman et all (2010)[15] to evaluate the parameters of Weighted Weibull distribution is considered here. Then, the cumulative distribution function is: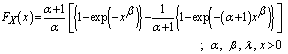 | (2.1) |
and the probability density function is: 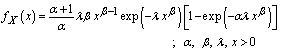 | (2.1) |
hence 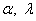 are shape parameters and
are shape parameters and 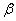 is scale parameter. Now, let
is scale parameter. Now, let 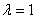 as the same used manner at Saman et all (2010)[15].This paper consists of three sections corresponding to sections 2, 3, and 4, respectively. section 2 provides an approach for scheming Stress-Stress reliability system. section 3, discusses the maximum likelihood Estimators, Least Square Estimators and Bayesian estimators of the reliability R. Finally a numerical investigation will be carried out to study the properties of the new estimators.
as the same used manner at Saman et all (2010)[15].This paper consists of three sections corresponding to sections 2, 3, and 4, respectively. section 2 provides an approach for scheming Stress-Stress reliability system. section 3, discusses the maximum likelihood Estimators, Least Square Estimators and Bayesian estimators of the reliability R. Finally a numerical investigation will be carried out to study the properties of the new estimators.
2. System Reliability
Let 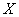 be the strength of a system and
be the strength of a system and  be the stress acting on it.
be the stress acting on it.  and
and  are the random variables from Weighted Weibull distributions with parameters
are the random variables from Weighted Weibull distributions with parameters 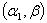 and
and 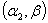 respectively. Therefore, the probability density functions of
respectively. Therefore, the probability density functions of 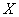 and
and 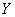 are, respectively:
are, respectively: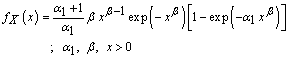 | (1.2) |
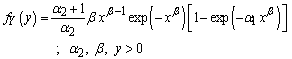 | (2.2) |
where  and
and  are shape parameters and
are shape parameters and  is scale parameter. Then, the reliability function
is scale parameter. Then, the reliability function  is:
is: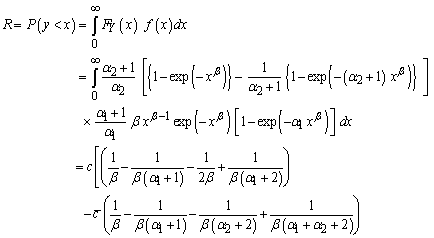 | (3.2) |
where 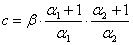 and
and 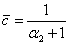 .
.
3. Point Estimator of the Reliability R
3.1. Maximum Likelihood Estimator
Let 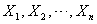 and
and 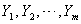 be the two independent random samples taken from the Weighted Weibull distributions with parameters
be the two independent random samples taken from the Weighted Weibull distributions with parameters 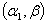 and
and 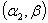 respectively, then, the likelihood and log-likelihood function based on the above samples are respectively given as:
respectively, then, the likelihood and log-likelihood function based on the above samples are respectively given as: 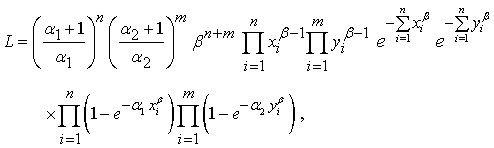 | (1.3) |
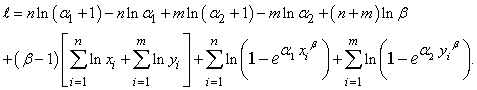 | (2.3) |
The derivatives of 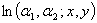 with respect to
with respect to  and
and 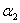 are, respectively:
are, respectively: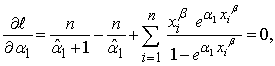 | (3.3) |
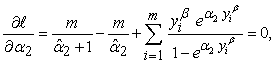 | (4.3) |
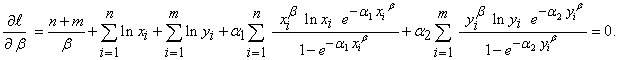 | (5.3) |
Unfortunately, there is no demand value for 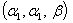 in (3.3), (4.3) and (5.3), so with that, Newton–Raphson method in an iterative approach to solve this equations in numerical analysis is considered. It is an iterative method for solving equations
in (3.3), (4.3) and (5.3), so with that, Newton–Raphson method in an iterative approach to solve this equations in numerical analysis is considered. It is an iterative method for solving equations 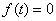 where
where 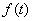 is assumed to have a continuous derivative
is assumed to have a continuous derivative 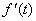 . Given a function
. Given a function 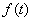 and its derivative
and its derivative  , a first guess
, a first guess 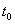 is initialed. Then, an approximation of
is initialed. Then, an approximation of 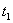 is
is  and an approximation of
and an approximation of  is
is 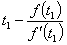 and so on for number of iterations r or if
and so on for number of iterations r or if  where
where  is the
is the 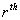 estimate.Now, replace
estimate.Now, replace  which gives from iteration with the parameter
which gives from iteration with the parameter 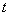 after iteration process for estimating the parameter
after iteration process for estimating the parameter  in equations (3.3), (4.3) and (5.3).Since, Maximum Likelihood Estimators are do not change, So it becomes:
in equations (3.3), (4.3) and (5.3).Since, Maximum Likelihood Estimators are do not change, So it becomes: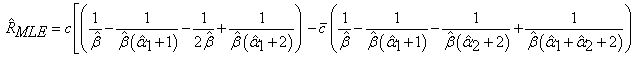 | (6.3) |
where 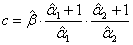 and
and  .
.
3.2. Least Square Estimators
Suppose that (2.1) is a linear relation between the two variables and take the logarithm of the two sides as follows: 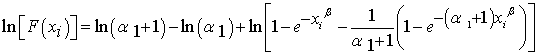 | (7.3) |
So, if this function is minimized with respect to  , we end up with the Least Square Estimators. This method is known as Least Square method (more details, see Flaih et al (2012)[8]. Now, using the mean rank method, we can estimate
, we end up with the Least Square Estimators. This method is known as Least Square method (more details, see Flaih et al (2012)[8]. Now, using the mean rank method, we can estimate  from this relation
from this relation  , where
, where 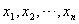 are the rank failure times.Let
are the rank failure times.Let  , so, (7.3) becomes straight line equation. Therefore, the least square estimators of
, so, (7.3) becomes straight line equation. Therefore, the least square estimators of  and
and 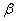 come from minimizing the following equation:
come from minimizing the following equation: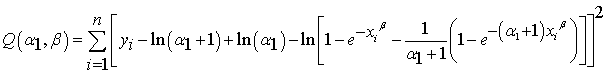 | (8.3) |
The first partial derivatives of 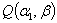 with respect to
with respect to  and
and 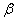 , respectively, are:
, respectively, are: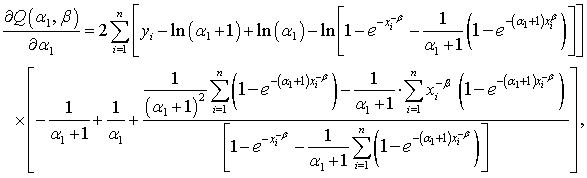 | (9.3) |
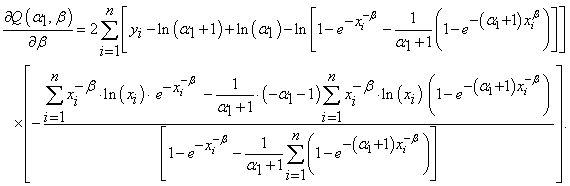 | (10.3) |
Similarly, the first partial derivatives of 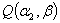 with respect to
with respect to 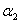 is:
is: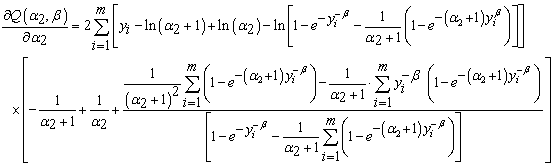 | (11.3) |
If both  ,
,  and
and 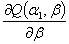 equal zero, then, the Least Square Estimators of
equal zero, then, the Least Square Estimators of 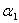 ,
,  and
and  will result immediately. However, this process is too difficult to be done without numerical solution. So, we adapt the previous technique of , Newton–Raphson method.
will result immediately. However, this process is too difficult to be done without numerical solution. So, we adapt the previous technique of , Newton–Raphson method.
3.3. Bayes Estimator of Reliability R
Let  and
and 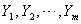 be two independent random samples, drawn from the Weighted Weibull distributions with parameters
be two independent random samples, drawn from the Weighted Weibull distributions with parameters 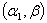 and
and 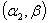 respectively, an associate gamma prior distributions for
respectively, an associate gamma prior distributions for 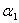 and
and 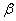 with parameters
with parameters 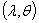 and
and  are employed respectively, so that the prior distribution for
are employed respectively, so that the prior distribution for 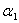 and
and 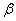 are:
are: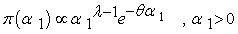 | (12.3) |
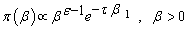 | (13.3) |
where  are independent. And the joint density function for data and the parameters
are independent. And the joint density function for data and the parameters  and
and  is:
is: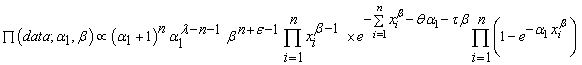 | (14.3) |
Then, the posterior density function for 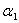 and
and 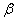 based on data is:
based on data is: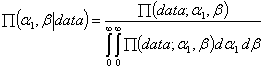 | (15.3) |
Now, by using Posterior Mode Method to obtain the Bayesian estimators of parameters as follows:The log posterior distribution for the sample 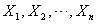 taken from Weighted Weibull distribution with Gamma priors
taken from Weighted Weibull distribution with Gamma priors  and
and 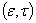 respectively is:
respectively is: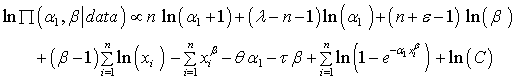 | (16.3) |
where C does not dependent on the parameters  and the parameters
and the parameters  and
and  are fixed.The first derivatives of
are fixed.The first derivatives of 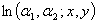 with respect to
with respect to  and
and  are, respectively:
are, respectively: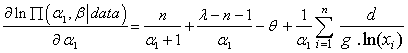 | (17.3) |
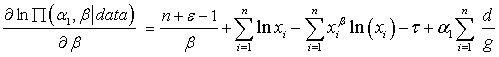 | (18.3) |
Let 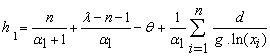 , and
, and 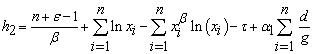 . Then,
. Then,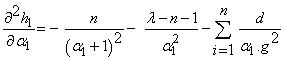 | (19.3) |
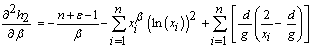 | (20.3) |
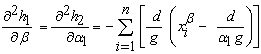 | (21.3) |
where 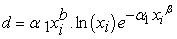
 . So, the Hessian matrix of the derivatives I is :
. So, the Hessian matrix of the derivatives I is :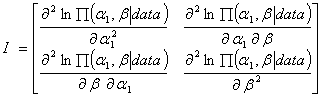 | (22.3) |
The object of this work is estimate 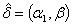 numerically to find
numerically to find 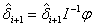 where
where  . Solution can be converged using Newton–Raphson algorithm to estimate
. Solution can be converged using Newton–Raphson algorithm to estimate  which are replaced by
which are replaced by 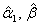 gleaned from iteration.
gleaned from iteration.
4. Simulation Study
Table (1). When
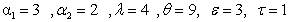 |
| | n | m | RMLE | RBN-IF | RB-IF | MSEMLE | MSEBN-IF | MSEB-IF | | 5 | 5 | 0.4063 | 0.3975 | 0.4094 | 0.0222 | 0.0182 | 0.017 | | 10 | 0.4179 | 0.3996 | 0.4256 | 0.0161 | 0.0142 | 0.0138 | | 20 | 0.4222 | 0.3993 | 0.4324 | 0.0155 | 0.0146 | 0.012 | | 30 | 0.4233 | 0.3988 | 0.4344 | 0.0119 | 0.014 | 0.0115 | | 10 | 5 | 0.3939 | 0.3988 | 0.3913 | 0.0156 | 0.0131 | 0.149 | | 10 | 0.4023 | 0.3977 | 0.4042 | 0.0095 | 0.0085 | 0.0081 | | 20 | 0.4059 | 0.3965 | 0.4102 | 0.00617 | 0.00571 | 0.0056 | | 30 | 0.4085 | 0.3976 | 0.4136 | 0.00511 | 0.00484 | 0.0048 | | 15 | 5 | 0.3852 | 0.3963 | 0.3798 | 0.0122 | 0.0104 | 0.0099 | | 10 | 0.3974 | 0.3999 | 0.3961 | 0.00601 | 0.00535 | 0.0051 | | 20 | 0.401 | 0.3986 | 0.402 | 0.00277 | 0.00253 | 0.0024 | | 30 | 0.4018 | 0.3979 | 0.4036 | 0.00194 | 0.00179 | 0.0017 | | 20 | 5 | 0.386 | 0.3996 | 0.3792 | 0.0112 | 0.0092 | 0.009 | | 10 | 0.3929 | 0.3976 | 0.3905 | 0.00471 | 0.00421 | 0.004 | | 20 | 0.3955 | 0.3955 | 0.3954 | 0.00182 | 0.00164 | 0.0016 | | 30 | 0.3992 | 0.3976 | 0.3999 | 0.00075 | 0.00065 | 0.0006 |
|
|
Table (2). When
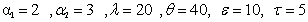 |
| | n | m | RMLE | RBN-IF | RB-IF | MSEMLE | MSEBN-IF | MSEB-IF | | 25 | 25 | 0.5807 | 0.5895 | 0.5777 | 0.0194 | 0.0234 | 0.0182 | | 50 | 0.5916 | 0.5869 | 0.5943 | 0.0139 | 0.0164 | 0.123 | | 75 | 0.5995 | 0.5881 | 0.6051 | 0.0111 | 0.0129 | 0.0105 | | 100 | 0.6027 | 0.5892 | 0.6094 | 0.0105 | 0.0122 | 0.0132 | | 50 | 25 | 0.5744 | 0.5926 | 0.5666 | 0.0152 | 0.0173 | 0.0148 | | 50 | 0.588 | 0.5927 | 0.5861 | 0.0087 | 0.0096 | 0.0083 | | 75 | 0.5926 | 0.5903 | 0.5938 | 0.0061 | 0.0068 | 0.0059 | | 100 | 0.5964 | 0.5918 | 0.5987 | 0.0051 | 0.0056 | 0.0048 | | 75 | 25 | 0.5677 | 0.5907 | 0.5575 | 0.0131 | 0.0141 | 0.0083 | | 50 | 0.5814 | 0.5907 | 0.5781 | 0.0067 | 0.0072 | 0.0132 | | 75 | 0.5898 | 0.5922 | 0.5887 | 0.0035 | 0.0037 | 0.0034 | | 100 | 0.5902 | 0.5902 | 0.5903 | 0.0028 | 0.0029 | 0.0027 | | 100 | 25 | 0.5636 | 0.5882 | 0.5526 | 0.0124 | 0.0491 | 0.0126 | | 50 | 0.5794 | 0.5903 | 0.5742 | 0.0057 | 0.0061 | 0.0054 | | 75 | 0.5842 | 0.5881 | 0.5825 | 0.0027 | 0.0028 | 0.0026 | | 100 | 0.5874 | 0.5889 | 0.5846 | 0.0018 | 0.0019 | 0.0017 |
|
|
The computer programs MathCAD (2001) is used to obtain numerical illustration for the last theoretical results. A comparison between the three estimators, MLE, Bayes based on non-informative estimator and Bayes based on informative estimator is performed . 200 samples generated from Weighted Weibull distributions with parameters  and
and 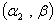 are used, respectively, and different values of
are used, respectively, and different values of 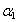 ,
, 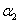 and
and 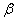 with various sizes
with various sizes 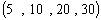 for both n and m in table 1. Also, various sizes
for both n and m in table 1. Also, various sizes 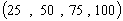 for them in table 2. Then the means of these replicates are calculated to obtain maximum likelihood estimator of R (RMLE), Bayes estimator based on non-informative (RBN-IF) and Bayes estimator based on informative RB-IF . The mean square error of RMLE, RBN-IF and RB-IF are computed as well.From Table (1) and (2), note that the mean square error of RB-IF is smaller than each of the mean square error of RMLE and RBN-IF if the sample sizes n, m are small or large. But, in table (2), when the sample sizes are large the mean square error of all estimators are less than the other. For example, when the sample sizes
for them in table 2. Then the means of these replicates are calculated to obtain maximum likelihood estimator of R (RMLE), Bayes estimator based on non-informative (RBN-IF) and Bayes estimator based on informative RB-IF . The mean square error of RMLE, RBN-IF and RB-IF are computed as well.From Table (1) and (2), note that the mean square error of RB-IF is smaller than each of the mean square error of RMLE and RBN-IF if the sample sizes n, m are small or large. But, in table (2), when the sample sizes are large the mean square error of all estimators are less than the other. For example, when the sample sizes  and
and 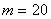 , we find that the mean square errors of RMLE and RBN-IF and RB-IF are (0.0155, 0.0148 and 0.0120) respectively, while, they are (0.0111, 0.0129 and 0.0105) when the sample sizes are
, we find that the mean square errors of RMLE and RBN-IF and RB-IF are (0.0155, 0.0148 and 0.0120) respectively, while, they are (0.0111, 0.0129 and 0.0105) when the sample sizes are  and
and 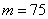 . This behavior applies on the rest of parameters
. This behavior applies on the rest of parameters 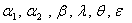 and
and  as well.Also, the three estimators RB-IF, RMLE and RBN-IF are increase with decreasing the sample size n and take the sample size m is fixed, and they are increase with decreasing the sample size m and take the sample size n is fixed. On the other hand, they are increase with decreasing both the sample sizes n and m.
as well.Also, the three estimators RB-IF, RMLE and RBN-IF are increase with decreasing the sample size n and take the sample size m is fixed, and they are increase with decreasing the sample size m and take the sample size n is fixed. On the other hand, they are increase with decreasing both the sample sizes n and m.
5. Conclusions
In this paper, the estimation problem of the reliability of a system R in stress-strength model when 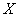 and
and 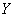 are independent variables distributed as Weighted Weibull Distribution is considered. Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators based on non-informative and informative prior distributions were discussed via numerical results.
are independent variables distributed as Weighted Weibull Distribution is considered. Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators based on non-informative and informative prior distributions were discussed via numerical results.
References
| [1] | Abd-Elfattah, A. M., Mandouh, R. M. (2004). Estimation of P(Y < X) in Lomax case. The 39th Annual Conference on Statistics, Computer Science and Operation Research, ISSR, Cairo University, Egypt, part 1, 156-166. |
| [2] | Akbar A. , Reza V. and Mohammad Z. (2012). Stress-strength reliability of Weibull distribution based on progressively censored samples3SORT 35 (2), 103-124. |
| [3] | Alam, S.N. and Roohi (2002): On augmenting exponential strength-reliability, IAPQR Transactions. 27, 111-117. |
| [4] | Alam, S.N. and Roohi (2003): On facing an exponential stress and strength having power function distribution. Aligarh J. Statistic. 23, 57-63. |
| [5] | Awad, A.M., Gharraf, M.K. (1986) Estimation of P(Y < X) in the Burr case: a comparative study. Commune. Statistic. - Simul. Comp., 15, 389-403. |
| [6] | Azzalini, A. (1985). A class of distributions which include the normal ones, Scand. J. Stat., Vol. 12, 171–178. |
| [7] | Baklizi A. (2012) Inference on 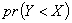 in the Two-Parameter Weibull Model Based on Records. International Scholarly Research Network. Volume 2012. doi:10.5402/2012/263612. in the Two-Parameter Weibull Model Based on Records. International Scholarly Research Network. Volume 2012. doi:10.5402/2012/263612. |
| [8] | Flaih, A. , Elsalloukh, H. , Mendi, and E. and Milanova, M. (2012). The Exponentiated Inverted Weibull Distribution. Appl. Math. Inf. Sci. 6, No. 2, 167-171. |
| [9] | Gupta, R. D. & Kundu, D. (2009). A new class of weighted exponential distributions, Statistics, 43(6), 621–634. |
| [10] | Johnson, R.A. (1988) Stress-strength Models for Reliability. In Handbook of Statistics. Ed. Krishnaiah, P.R. and Rao, C.R., Vol. 7, Elsevier, North Holland, 27-54. |
| [11] | Khan, M.A. and Islam, H.M. (2007): On facing Rayleigh stress with strength having power function distribution. J. Appl. Statist. Sci. 16 pp. 159-168. |
| [12] | Kotz, S., Lumelskii, Y. and Pensky, M. (2003). The Stress-Strength Model and Its Generalizations. New Jersey: World Scientific, Inc. |
| [13] | Makhdoom, I. (2012). Estimation of  for Weighted Exponential Distribution. J. Applied Sci. 12 (13). 1384 - 1389. for Weighted Exponential Distribution. J. Applied Sci. 12 (13). 1384 - 1389. |
| [14] | Mokhlis, N. A. (2005) Reliability of a Stress-Strength Model with Burr Type III Distributions. Comm. Statist. - Theory Meth., 34, 1643-1657. |
| [15] | Saman, S., Muhammad, Q. & Nadeem, S. (2010). A class of Weighted Weibull Distribution. Pak. j. stat. oper. res. Vol. VI No.1 2010 pp53-59. Electronic copy available at:http://ssrn.com/abstract=1727489. |

 when
when  and
and 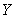 are independent variables distributed as Weighted Weibull Distribution. Different methods for estimating the reliability are obtained such as Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators which are based on non-informative and informative prior distributions. A comparison of the estimates obtained is performed as well. Finally a numerical investigation is carried out to study the properties of the new estimators.
are independent variables distributed as Weighted Weibull Distribution. Different methods for estimating the reliability are obtained such as Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators which are based on non-informative and informative prior distributions. A comparison of the estimates obtained is performed as well. Finally a numerical investigation is carried out to study the properties of the new estimators.
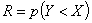 arises in the situation of mechanical reliability of a system with strength
arises in the situation of mechanical reliability of a system with strength 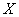 and stress
and stress 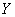 , and R is a determine of system reliability. The system fails if and only if, at any time the stress exceeds the strength.Many authors have measured different choices for stress and strength distributions. Johnson (1988)[10] summarized some of these choices. Awad & Gharraf (1986)[5] considered the case when
, and R is a determine of system reliability. The system fails if and only if, at any time the stress exceeds the strength.Many authors have measured different choices for stress and strength distributions. Johnson (1988)[10] summarized some of these choices. Awad & Gharraf (1986)[5] considered the case when  and
and 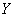 are independent and have Burr Type XII random variables. They obtained a maximum likelihood estimator, minimum variance unbiased estimator, and a Bayesian estimator for R. They used a numerical procedure for evaluating their Bayesian estimator. Alam & Roohi (2002)[3] studied stress and strength having exponential distribution but in (2003)[4] have studied the problem of
are independent and have Burr Type XII random variables. They obtained a maximum likelihood estimator, minimum variance unbiased estimator, and a Bayesian estimator for R. They used a numerical procedure for evaluating their Bayesian estimator. Alam & Roohi (2002)[3] studied stress and strength having exponential distribution but in (2003)[4] have studied the problem of 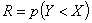 in a different way. They have set up the required parametric values of the assumed distributions as a replacement for finding P (Y
in a different way. They have set up the required parametric values of the assumed distributions as a replacement for finding P (Y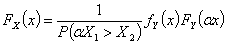
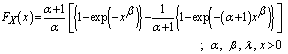
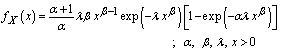
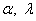 are shape parameters and
are shape parameters and 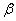 is scale parameter. Now, let
is scale parameter. Now, let 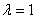 as the same used manner at Saman et all (2010)[15].This paper consists of three sections corresponding to sections 2, 3, and 4, respectively. section 2 provides an approach for scheming Stress-Stress reliability system. section 3, discusses the maximum likelihood Estimators, Least Square Estimators and Bayesian estimators of the reliability R. Finally a numerical investigation will be carried out to study the properties of the new estimators.
as the same used manner at Saman et all (2010)[15].This paper consists of three sections corresponding to sections 2, 3, and 4, respectively. section 2 provides an approach for scheming Stress-Stress reliability system. section 3, discusses the maximum likelihood Estimators, Least Square Estimators and Bayesian estimators of the reliability R. Finally a numerical investigation will be carried out to study the properties of the new estimators.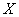 be the strength of a system and
be the strength of a system and  be the stress acting on it.
be the stress acting on it.  and
and  are the random variables from Weighted Weibull distributions with parameters
are the random variables from Weighted Weibull distributions with parameters 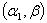 and
and 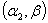 respectively. Therefore, the probability density functions of
respectively. Therefore, the probability density functions of  and
and  are, respectively:
are, respectively: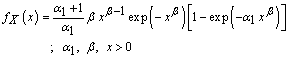
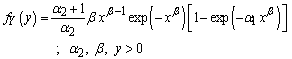
 and
and  are shape parameters and
are shape parameters and  is scale parameter. Then, the reliability function
is scale parameter. Then, the reliability function  is:
is: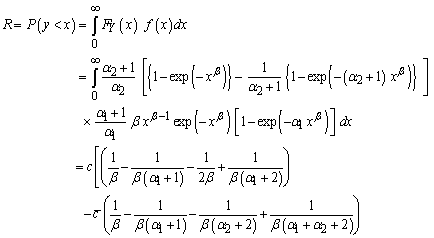
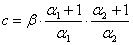 and
and 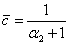 .
.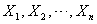 and
and 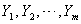 be the two independent random samples taken from the Weighted Weibull distributions with parameters
be the two independent random samples taken from the Weighted Weibull distributions with parameters 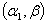 and
and 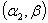 respectively, then, the likelihood and log-likelihood function based on the above samples are respectively given as:
respectively, then, the likelihood and log-likelihood function based on the above samples are respectively given as: 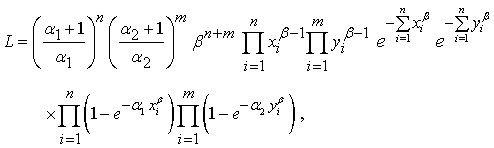
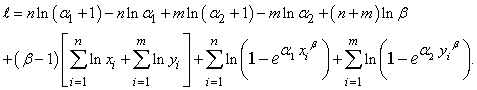
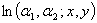 with respect to
with respect to  and
and 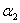 are, respectively:
are, respectively: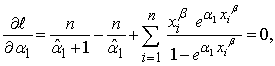
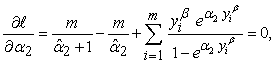
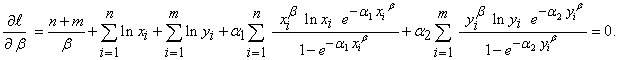
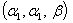 in (3.3), (4.3) and (5.3), so with that, Newton–Raphson method in an iterative approach to solve this equations in numerical analysis is considered. It is an iterative method for solving equations
in (3.3), (4.3) and (5.3), so with that, Newton–Raphson method in an iterative approach to solve this equations in numerical analysis is considered. It is an iterative method for solving equations 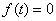 where
where 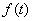 is assumed to have a continuous derivative
is assumed to have a continuous derivative 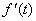 . Given a function
. Given a function 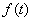 and its derivative
and its derivative  , a first guess
, a first guess 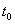 is initialed. Then, an approximation of
is initialed. Then, an approximation of 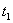 is
is  and an approximation of
and an approximation of  is
is 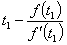 and so on for number of iterations r or if
and so on for number of iterations r or if  where
where  is the
is the 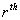 estimate.Now, replace
estimate.Now, replace  which gives from iteration with the parameter
which gives from iteration with the parameter 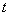 after iteration process for estimating the parameter
after iteration process for estimating the parameter  in equations (3.3), (4.3) and (5.3).Since, Maximum Likelihood Estimators are do not change, So it becomes:
in equations (3.3), (4.3) and (5.3).Since, Maximum Likelihood Estimators are do not change, So it becomes: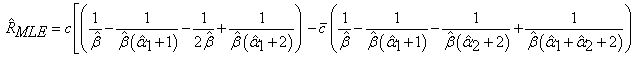
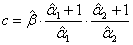 and
and  .
.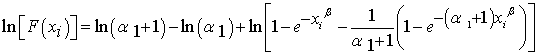
 , we end up with the Least Square Estimators. This method is known as Least Square method (more details, see Flaih et al (2012)[8]. Now, using the mean rank method, we can estimate
, we end up with the Least Square Estimators. This method is known as Least Square method (more details, see Flaih et al (2012)[8]. Now, using the mean rank method, we can estimate  from this relation
from this relation  , where
, where 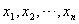 are the rank failure times.Let
are the rank failure times.Let  , so, (7.3) becomes straight line equation. Therefore, the least square estimators of
, so, (7.3) becomes straight line equation. Therefore, the least square estimators of  and
and 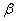 come from minimizing the following equation:
come from minimizing the following equation: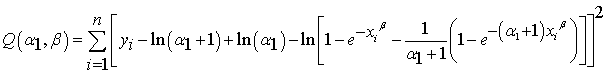
 with respect to
with respect to  and
and  , respectively, are:
, respectively, are: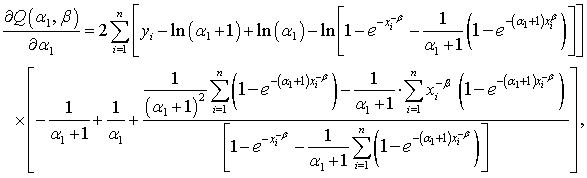
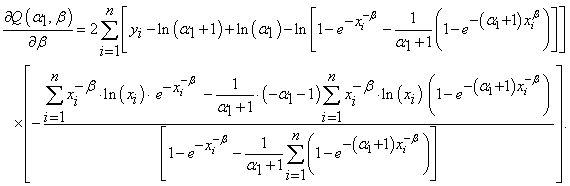
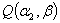 with respect to
with respect to 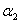 is:
is: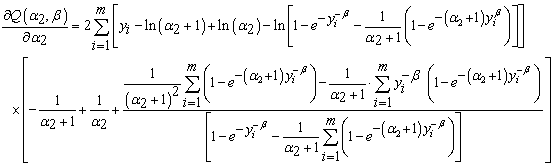
 ,
,  and
and 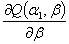 equal zero, then, the Least Square Estimators of
equal zero, then, the Least Square Estimators of 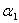 ,
,  and
and  will result immediately. However, this process is too difficult to be done without numerical solution. So, we adapt the previous technique of , Newton–Raphson method.
will result immediately. However, this process is too difficult to be done without numerical solution. So, we adapt the previous technique of , Newton–Raphson method. and
and 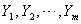 be two independent random samples, drawn from the Weighted Weibull distributions with parameters
be two independent random samples, drawn from the Weighted Weibull distributions with parameters 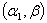 and
and 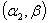 respectively, an associate gamma prior distributions for
respectively, an associate gamma prior distributions for 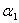 and
and 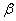 with parameters
with parameters 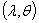 and
and  are employed respectively, so that the prior distribution for
are employed respectively, so that the prior distribution for 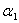 and
and 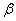 are:
are: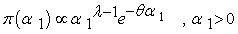
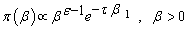
 are independent. And the joint density function for data and the parameters
are independent. And the joint density function for data and the parameters  and
and  is:
is: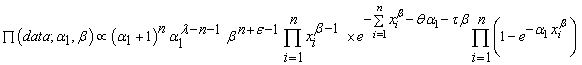
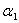 and
and 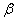 based on data is:
based on data is: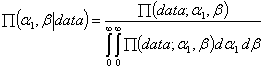
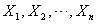 taken from Weighted Weibull distribution with Gamma priors
taken from Weighted Weibull distribution with Gamma priors  and
and 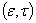 respectively is:
respectively is: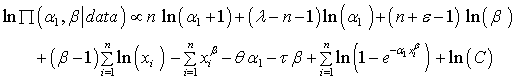
 and the parameters
and the parameters  and
and  are fixed.The first derivatives of
are fixed.The first derivatives of 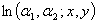 with respect to
with respect to  and
and 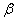 are, respectively:
are, respectively: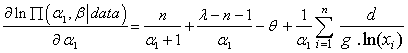
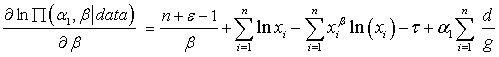
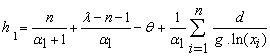 , and
, and 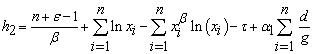 . Then,
. Then,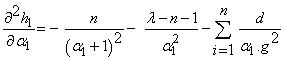
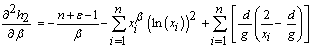
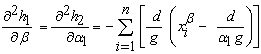
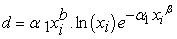
 . So, the Hessian matrix of the derivatives I is :
. So, the Hessian matrix of the derivatives I is :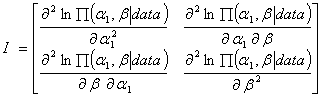
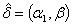 numerically to find
numerically to find 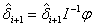 where
where  . Solution can be converged using Newton–Raphson algorithm to estimate
. Solution can be converged using Newton–Raphson algorithm to estimate  which are replaced by
which are replaced by 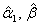 gleaned from iteration.
gleaned from iteration. and
and 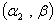 are used, respectively, and different values of
are used, respectively, and different values of 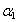 ,
, 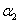 and
and 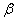 with various sizes
with various sizes 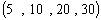 for both n and m in table 1. Also, various sizes
for both n and m in table 1. Also, various sizes 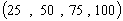 for them in table 2. Then the means of these replicates are calculated to obtain maximum likelihood estimator of R (RMLE), Bayes estimator based on non-informative (RBN-IF) and Bayes estimator based on informative RB-IF . The mean square error of RMLE, RBN-IF and RB-IF are computed as well.From Table (1) and (2), note that the mean square error of RB-IF is smaller than each of the mean square error of RMLE and RBN-IF if the sample sizes n, m are small or large. But, in table (2), when the sample sizes are large the mean square error of all estimators are less than the other. For example, when the sample sizes
for them in table 2. Then the means of these replicates are calculated to obtain maximum likelihood estimator of R (RMLE), Bayes estimator based on non-informative (RBN-IF) and Bayes estimator based on informative RB-IF . The mean square error of RMLE, RBN-IF and RB-IF are computed as well.From Table (1) and (2), note that the mean square error of RB-IF is smaller than each of the mean square error of RMLE and RBN-IF if the sample sizes n, m are small or large. But, in table (2), when the sample sizes are large the mean square error of all estimators are less than the other. For example, when the sample sizes  and
and 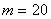 , we find that the mean square errors of RMLE and RBN-IF and RB-IF are (0.0155, 0.0148 and 0.0120) respectively, while, they are (0.0111, 0.0129 and 0.0105) when the sample sizes are
, we find that the mean square errors of RMLE and RBN-IF and RB-IF are (0.0155, 0.0148 and 0.0120) respectively, while, they are (0.0111, 0.0129 and 0.0105) when the sample sizes are  and
and 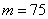 . This behavior applies on the rest of parameters
. This behavior applies on the rest of parameters 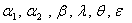 and
and  as well.Also, the three estimators RB-IF, RMLE and RBN-IF are increase with decreasing the sample size n and take the sample size m is fixed, and they are increase with decreasing the sample size m and take the sample size n is fixed. On the other hand, they are increase with decreasing both the sample sizes n and m.
as well.Also, the three estimators RB-IF, RMLE and RBN-IF are increase with decreasing the sample size n and take the sample size m is fixed, and they are increase with decreasing the sample size m and take the sample size n is fixed. On the other hand, they are increase with decreasing both the sample sizes n and m.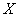 and
and 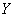 are independent variables distributed as Weighted Weibull Distribution is considered. Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators based on non-informative and informative prior distributions were discussed via numerical results.
are independent variables distributed as Weighted Weibull Distribution is considered. Maximum Likelihood Estimators, Least Square Estimators and Bayesian Estimators based on non-informative and informative prior distributions were discussed via numerical results.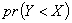 in the Two-Parameter Weibull Model Based on Records. International Scholarly Research Network. Volume 2012. doi:10.5402/2012/263612.
in the Two-Parameter Weibull Model Based on Records. International Scholarly Research Network. Volume 2012. doi:10.5402/2012/263612. for Weighted Exponential Distribution. J. Applied Sci. 12 (13). 1384 - 1389.
for Weighted Exponential Distribution. J. Applied Sci. 12 (13). 1384 - 1389. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML