-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(4): 213-219
doi:10.5923/j.ajms.20130304.05
On the Estimation of Survival of HIV/AIDS Patients on Antiretroviral Therapy Using NPMLE Method: An Application to Interval Censored Data
Gurprit Grover1, Rabindranath Das2, Prafulla Kumar Swain1, Barnali Deka1
1Department of Statistics, University of Delhi, Delhi, India
2Department of Statistics, University of Burdwan, West Bengal, India
Correspondence to: Prafulla Kumar Swain, Department of Statistics, University of Delhi, Delhi, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The main objective of this paper is to estimate the survival of HIV/AIDS patients who are undergoing Antiretroviral Therapy in an ART centre, Delhi. Non Parametric Maximum Likelihood Estimation NPMLE (E-M) for interval censoring and KM survival plot for left, right and mid-point imputation have been used to estimate the survival of these patients. It has been observed that the mid-point imputed survival plot has a very similar and consistent pattern as obtained by NPMLE (E-M) method. Considering these mid-point imputed value as right censored data, Cox PH model and Accelerated Failure time Model (AFTM) have been applied to identify the effects of prognostic factors like age, sex, mode of transmission, baseline CD4 cell count, hemoglobin, baseline weight and smoking habits on survival of the patients. The Akaike Information Criterion (AIC) has been employed to compare the efficiency of these models and Cox-Snell residual is used to test the proportionality assumption.
Keywords: AIDS, ART, CD4 Cell Count, Non Parametric Maximum Likelihood Estimation, Cox-PH Model, Accelerated Failure Time Model
Cite this paper: Gurprit Grover, Rabindranath Das, Prafulla Kumar Swain, Barnali Deka, On the Estimation of Survival of HIV/AIDS Patients on Antiretroviral Therapy Using NPMLE Method: An Application to Interval Censored Data, American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 213-219. doi: 10.5923/j.ajms.20130304.05.
Article Outline
1. Introduction
- The widespread use of Antiretroviral Therapy (ART), prognosis of HIV infected patients has significantly improved and mortality due to AIDS related causes has substantially reduced[1, 2, 3]. With the advent of free ART programme in 2004 in India, a dramatic decline of HIV incidence has been observed during the last decade[4]. Thus it is imperative to know the survival of HIV/AIDS patients on ART, so that appropriate strategies can be devised to prevent new infection.However in HIV/AIDS studies, where time to event data are collected by assessing patients in periodic follow up visits. In such cases, the event cannot be observed exactly (i.e onset of HIV infection, incubation period of AIDS after HIV infection, death time); however it is known to happen within some interval, thus such observed events are interval censored. In HIV dynamics every patient is supposed to visit ART centre after four weeks, but actual visit time vary from patient to patient and also time between visits vary. The patients may visit ART centre at time that is convenient to them rather than scheduled time. Therefore the failure event (i.e death) is considered as interval censored survival data. Survival time Ti (say) of a patient lies in the interval (Li , Ri) that is the last available visit date and end of the study.Several approaches have been proposed for the estimation of survival function for the interval censored data; Turnbull[5], De Gruttola and Lagakos[6] and Sun[7, 8]. More recently Kim[9], Grover and Shakeri[10], Grover and Banerjee[11] estimated survival of HIV-1 infected children for doubly and interval censored data.In this paper we have estimated the survival function of HIV/AIDS patients on ART by using Non Parametric Maximum Likelihood Estimation (NPMLE) method for interval censored data. The NPMLE is computed by using the E-M algorithm of Turnbull (1976) with the polishing algorithm of Gentleman and Geyer[12]. We have also estimated survival function by using imputation technique. Due to lack of appropriate estimation procedure and non availability of statistical software for interval censored data, we have adopted conventional imputation approach to convert interval censored data to right censored data, for which the standard techniques are available. Further, we have compared the estimates obtained by NPMLE and imputation method.Kaplan-Meier plot for left, right and mid-point imputation has been used to estimate the survival of patients. It has been observed that that the mid-point imputed survival plot has a very similar and consistent pattern as obtained by NPMLE (E-M) method. Considering these mid-point imputed values as right censored data at each interval, Cox Proportional Hazard model and Accelerated Failure Time Model (AFTM) has been used to study the effect of prognostic factors like age, sex, mode of transmission, baseline CD4 cell count, hemoglobin, baseline weight and smoking habits on the survival of patients.The semi parametric Cox PH model is the most common approach in survival analysis and has been used to evaluate the covariate effects on hazard function of failure time data. Interestingly, the result from a PH model is difficult to interpret in terms of survivorship. However, parametric AFTM is being treated as best attractive alternative to Cox PH model. AFT model provides concise and more intuitively interpretable results of survival data[13]. Since no one has used AFTM in HIV population studies in India earlier, we have modeled HIV/AIDS population on ART by using AFTM and compared the results with Cox PH model.The Akaike Information Criterion (AIC) has been employed to compare the efficiency of models. Schoenfeld residual and Cox-Snell residual method has also been used to test proportionality assumption. The software packages survival and interval in R and STATA(version 11.1) have been used to perform the statistical analyses.
2. Methods Used
2.1. NPMLE for Interval Censored Data
- Suppose that n number of HIV/AIDS patients are under ART, Let Ti be the survival time (i.e occurrence of death) of ith patient with survival function S(t). Let (Li , Ri) be the interval in which Ti is being observed, such that Li < Ti
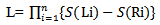 | (1) |
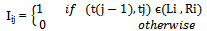 and P(tj) =P[ t(j-1)
and P(tj) =P[ t(j-1)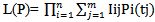 | (2) |
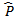 , by using EM algorithm[14]. Starting with initial estimate
, by using EM algorithm[14]. Starting with initial estimate 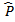 ,E-step, for each i
,E-step, for each i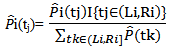 M-step: update
M-step: update 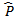 for each j
for each j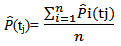 Iterate the procedure until convergence.
Iterate the procedure until convergence.2.2. Imputation Approach and K-M Survival Plot
- For simplicity, imputation techniques have been used to handle this interval censored data. After imputation the interval censored data will be treated as complete or right censored data, then standard statistical methods can be performed on the imputed data set (Hsu et al.,[15]).[16, 17] have used mid-point imputation for interval censored AIDS infection time data. Since the survival time Ti is known to lie in the interval {(Li , Ri) , i= 1,2…n} for ith patient. we use the midpoint (mi) of the observed interval as the hypothetical failure time i.e
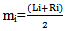 . And also an alternative to midpoint imputation is to take Ti as Li the left end point and Ri the right end point imputation have been used.Kaplan-Meier survival estimate have been plotted for this imputed data, by using the formula
. And also an alternative to midpoint imputation is to take Ti as Li the left end point and Ri the right end point imputation have been used.Kaplan-Meier survival estimate have been plotted for this imputed data, by using the formula 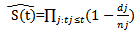 | (3) |
2.3. Cox-PH Model
- The Cox proportional hazard function[18] for the survival time T and the explanatory variables X is given by
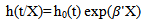 | (4) |
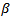 in the model can be estimated by maximizing the partial likelihood function;
in the model can be estimated by maximizing the partial likelihood function;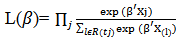 | (5) |
2.4. Accelerated Failure Time Model (AFTM)
- Accelerated Failure Time Model[19] assumes a linear relationship between logarithm of survival time and covariates, is given by
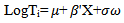 | (6) |
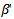 is a vector of regression coefficients,
is a vector of regression coefficients, 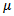 and
and 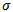 are intercept and scale parameters respectively and the error term
are intercept and scale parameters respectively and the error term 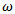 is assumed to have some distribution(i.e extreme value, normal or logistic). This transformation leads to the Weibull, Lognormal or log logistic AFT models for Ti[20].Now, the survivor function of Ti is given by
is assumed to have some distribution(i.e extreme value, normal or logistic). This transformation leads to the Weibull, Lognormal or log logistic AFT models for Ti[20].Now, the survivor function of Ti is given by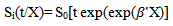 | (7) |
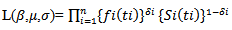 where fi(ti) and Si(ti) are the density and survival function for ith patients at time ti, and δi is the event indicator function, such that
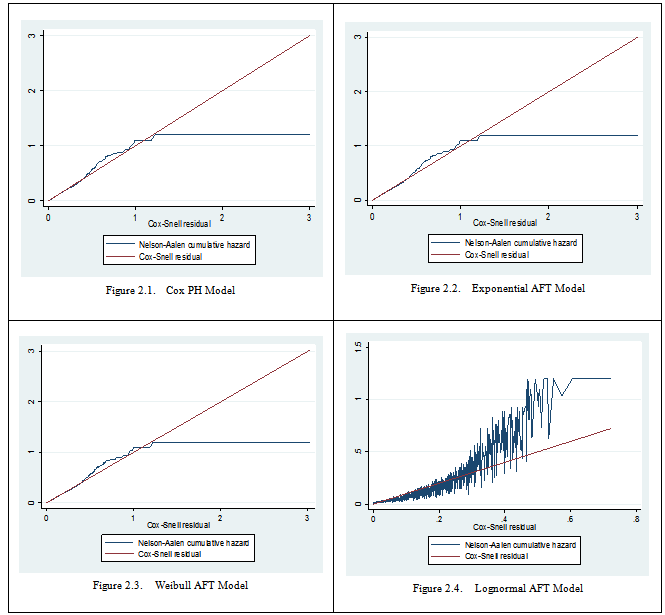
where fi(ti) and Si(ti) are the density and survival function for ith patients at time ti, and δi is the event indicator function, such that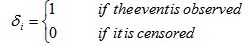 Results obtained from AFT models can be summarized in the exponentiated form as time ratio (i.e TR(=exp(
Results obtained from AFT models can be summarized in the exponentiated form as time ratio (i.e TR(=exp(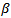 )) unlike Cox model hazard ratio. Thus TR>1, associated with prolonged survival time and TR<1, associated with a decrease in survival time.
)) unlike Cox model hazard ratio. Thus TR>1, associated with prolonged survival time and TR<1, associated with a decrease in survival time.2.5. Model Comparison
- In order to compare parametric AFTM and semi parametric Cox PH Model, we have used Akaike Information Criterion (AIC). The AIC which is a measure of goodness of fit of an estimated statistical model is given byAIC= -2*Log-likelihood +2(p+k)where p is the number of covariates in the model, k=1 for exponential and k=2 for weibull and lognormal models. Model with smaller AIC regarded as a better model.
3. Data Sources
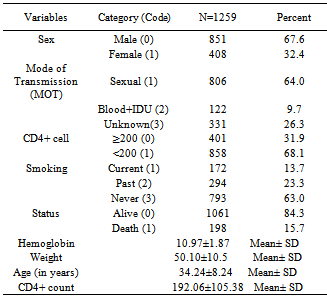
- A retrospective follow-up study was conducted, involving 1259 HIV/AIDS patients who were undergoing Antiretroviral Therapy in the ART centre of Dr. Ram Manohar Lohia Hospital, New Delhi, India, during the period of April 2004 to November 2009, and were followed up through the ART routine register records till December 2010. Taking preliminary inclusion criteria as patients should be above 18 years of age and on the basis of availability of complete baseline information on CD4 cell count, date of visit, mode of transmission, weight and hemoglobin etc, 1259 patients were found eligible for the analysis. At the end of the study period, 198 patients were dead and remaining 1061 patients were known to be alive, since the exact date of death is not known, the event death is known to lie in an interval that is the last available CD4 count date and end of the study. Thus the observed event leads to interval censored survival data.Table 1: presents the descriptive statistics of the study, out of 1259 patients 408 (32.4%) were female. The mean age at diagnosis was 34.24(±8.74) years and the most common mode of transmission was sexual (hetro+homo) 64.0%, and for 331(26.3%) patients mode of transmission were unknown. 858(68.1%) patients had CD4 cell count less than 200 cell/mm3 at the time of enrollment. 198 (15.7%) patients died and remaining were alive at the end of the study.
|
 | Figure 1. Estimated survival function based on intervals and imputation |
|
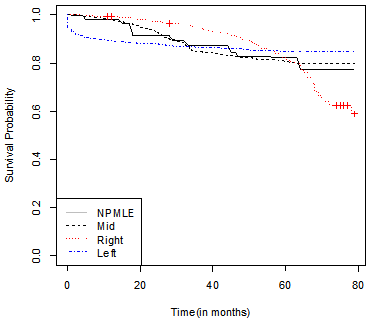
 | Figure 2. Cumulative hazard plot of Cox-Snell residual for AFT models |
|
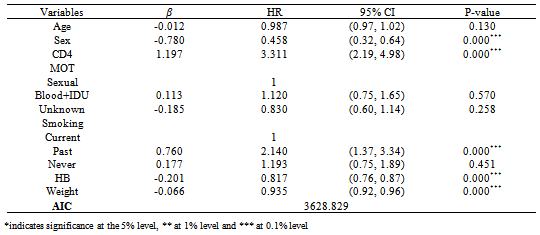
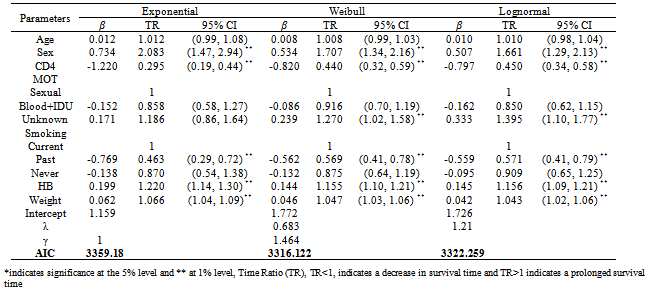
- The parametric AFTM results have been presented in table 3, besides the factors found significant in Cox model, unknown mode of transmission was also found to be a significant predictor in Weibull and lognormal AFT model. Patients who had CD4 cell count<200 cells/mm3 have shorter survival time than patients with CD4 cell count more than 200 cells/mm3 (as TR<1), female patients had longer survival than their male counterparts (TR>1). An increase in survival time was associated with per unit increase in hemoglobin. Old aged patients had shorter survival than young patients, and also an increase in weight (in kg) leads to increase in life expectancy.According to Akaike Information Criterion (AIC), Weibull AFTM was found to be better (smallest AIC) one among the parametric and Cox model. Proportional assumptions were hold (confirmed by Schoenfeld residual plot, not shown here) and the Cox-Snell residual fitted well to all the AFT models shown figure 2.
4. Discussion
- In this study we have tried to estimate the survival of HIV/AIDS patients under interval censoring mechanism, since the event of interest death lie in an interval i.e the last available CD4 count date and end of the study. Due to lack of well known statistical methodology and available statistical software, we have adopted imputation approach to handle interval censored data, so that the interval censored data converts to right censored data to which the standard technique can be applied. We have observed that survival function obtained by NPMLE (E-M) for interval censored data has a very close resemblance to the survival function obtained at the mid-point of the interval by Kaplan-Meier method. This is corroborated with the findings of previous studies[10, 17]. However our aim was to determine the effects of prognostic factors age, sex, MOT, baseline CD4 cell, baseline hemoglobin, baseline weight and smoking habits on the survival.The prognostic factors viz. sex, CD4 cell count, past smokers, baseline hemoglobin and baseline weight are found to be statistically significant (P< 0.000) by both semi parametric Cox PH and parametric AFT Model. Most of the previous studies have suggested that the age is a significant prognostic factor[21, 22, 23]. As age increases the survival time of HIV/AIDS patients decreases. Old age is associated with high risk of disease progression but in our analysis age is not found to be a significant prognostic factor. Also females are observed to have better survival than their male counterpart. As reported previously female had higher life expectancies than male[21, 24, 25, 26]. Remafedi et al.[27], had proposed that sex of the patients does not have any significant effect on survival time.Consistent with the published literature CD4 cell count is found to be an important prognostic marker of HIV/AIDS patients. Patients with CD4 cell <200 cells/mm3 have 3.31 times more hazard to die than patient who had CD4 cell more than 200 cells/mm3. The mortality is inversely proportional to CD4 count, cumulative probability of AIDS and death increased substantially with decreasing CD4 cell count[23, 28, 29].Another important result of our study is that patients with sexual (hetro or homo) mode of transmission had worst survival than patients with blood and intravenous drug user mode of transmission, which is departed from earlier result of[21]. where they found that intravenous drug user mode of infection had worst survival. However, Remafedi et al[27] have shown that there were no significant differences between deceased and other subjects in relation to mode of transmission. Unknown mode of transmission was found to be a significant factor in weibull AFTM and Lognormal AFTM result. Patients who are current smokers had association with more hazards of immune deterioration. We found that baseline hemoglobin was a significant predictor of HIV/ AIDS patients. To our knowledge hemoglobin has never shown to predict mortality of patients on ART in India, further studies needed to confirm our findings. Baseline hemoglobin level can be used as a simple and practical tool for initial risk assessment in the absence of CD4 cell count and viral load, as was identified in earlier studies by[30] in Tanzania and[31] in Europe. Patient’s weight is positively associated with survival, this is corroborating to the findings of[22] that patients improved clinically with regard to weight and hemoglobin.There are many situations where AFTM provides better description of data than Cox PH model[32, 33, 34]. Our aim of this study was to compare the performance of both semi-parametric Cox PH model and Parametric AFTM. Based on AIC, Weibull AFT model is found to be efficient (smallest AIC) among the parametric and Cox PH model.There are some limitations of our study, firstly complete information on patients treatment, follow up data on clinical parameter were not available. Secondly, we have analyzed only one ART centre data, so generalization of our findings would need further conformity.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML