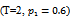Abas Lafta1, Suaad Khalaf Salman2, Nathier Ibrahim3
1Dean, College of Administration & Economic, Wasit University, Iraq
2Department of Mathematics, College of Education for pure Sciences, Karbala University, Iraq
3Economics and Mathematics, Design, Business Administration, Al-Nahrain University, Iraq
Correspondence to: Nathier Ibrahim, Economics and Mathematics, Design, Business Administration, Al-Nahrain University, Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
AbstractThis paper deals with a new probability distribution obtained from mixing Pareto (two parameters 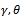 ) with Wiebull (two Parameters
) with Wiebull (two Parameters 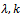 ), using mixing proportion
), using mixing proportion 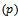 . The researcher construct the probability density function, and cumulative distribution function, reliability, hazard functions, moments are obtained the parameters which estimated by moment method (MOM) and maximum likelihood method (MLE) using simulation procedure taking different sample size
. The researcher construct the probability density function, and cumulative distribution function, reliability, hazard functions, moments are obtained the parameters which estimated by moment method (MOM) and maximum likelihood method (MLE) using simulation procedure taking different sample size 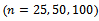 and replicate
and replicate 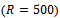 for each experiment.The comparison has been done through mean squares error (MSE).
for each experiment.The comparison has been done through mean squares error (MSE).
Keywords:
KeywordsMixture distribution (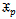 ), Pareto and Weibull, Moment Estimators, Maximum Likelihood Estimators, Mean Squares Error, Reliability
), Pareto and Weibull, Moment Estimators, Maximum Likelihood Estimators, Mean Squares Error, Reliability
Cite this paper: Abas Lafta, Suaad Khalaf Salman, Nathier Ibrahim, Estimating Parameters and Reliability for a New Mixture Distribution 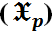 , American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 204-212. doi: 10.5923/j.ajms.20130304.04.
, American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 204-212. doi: 10.5923/j.ajms.20130304.04.
1. Introduction [3][6][7]
A mixture distribution is a compounding of statistical distributions, which arise when sampling frominhomogeneous populations (or mixed populations) with a different probability density function in each component.For example the distribution of times to failure in a mixture of good and defective items, and the distribution of some diagnostic measure in a mixed population of patients, some of whom have a given disease and some of them do not have. The application of finite mixture models arise in economics, medicine, psychology, agriculture, life testing and reliability. In many applications, the available data can be considered as data coming from a mixture population of two or more distributions.This idea enables us to mix statistical distribution to get a new distribution carrying the properties of its components. The distribution constructed here is denoted by (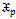 ), mixture of two parameters Pareto and two parameters Weibull.
), mixture of two parameters Pareto and two parameters Weibull.
2. Distribution
Here the 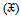 distribution is a mixture of some distributions with Weibull distribution, like exponential Weibull, Pareto Weibull, ErlangWeibull, Gamma Weibull. Now we explain
distribution is a mixture of some distributions with Weibull distribution, like exponential Weibull, Pareto Weibull, ErlangWeibull, Gamma Weibull. Now we explain 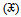 distribution which is a mixture of Pareto distribution with Weibull distribution and we shall denoted it by
distribution which is a mixture of Pareto distribution with Weibull distribution and we shall denoted it by 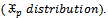 The statistical properties of (
The statistical properties of (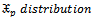 ) are explained, then we want to estimate its parameters;a. The probability density function
) are explained, then we want to estimate its parameters;a. The probability density function 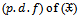 is;
is;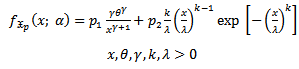 | (1) |
(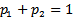 ) parameters of
) parameters of 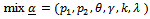 vector of parameters.b. The cumulative distribution function
vector of parameters.b. The cumulative distribution function 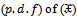 is;
is;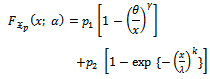 | (2) |
Also this function can be drawn for various values of parameters.The reliability function of (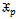 ) distribution denoted by;
) distribution denoted by; 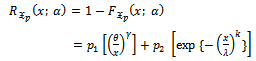 | (3) |
c. The hazard function of (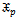 ) is;
) is;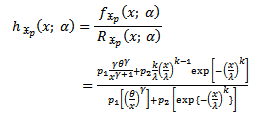 | (4) |
d. The 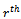 moment about origin of (
moment about origin of (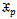 ) distribution which can be used in estimation method are defined as;
) distribution which can be used in estimation method are defined as;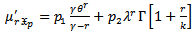 | (5) |
Where; 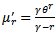 existing only for
existing only for 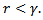 The mean and variance of (
The mean and variance of (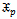 ) distribution can be obtained from (5), where;
) distribution can be obtained from (5), where;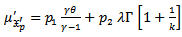 | (6) |
While the variance of (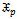 ) is;
) is;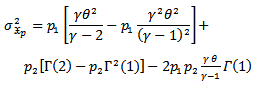 | (7) |
To estimate parameters by moments we must find, 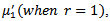 and another four moments.
and another four moments.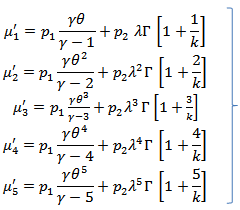 | (8) |
When 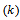 is integer
is integer 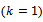 for example then solving these equations yield moment estimator.
for example then solving these equations yield moment estimator.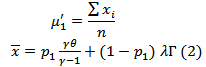 | (9) |
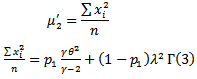 | (10) |
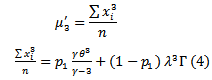 | (11) |
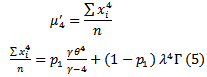 | (12) |
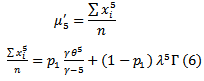 | (13) |
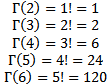 Here we assumed
Here we assumed 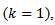 if we assume
if we assume 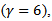 the parameters reduced to
the parameters reduced to 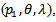 since
since 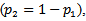 so we construct three equations for moment methods;
so we construct three equations for moment methods;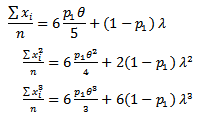 Assume
Assume 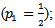
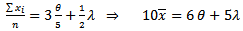 | (14) |
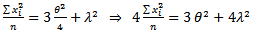 | (15) |
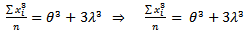 | (16) |
From equation (14), find 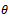 If
If 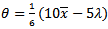 , substitute in (15);
, substitute in (15);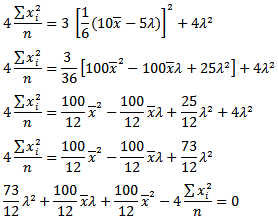 By using fixed point method where
By using fixed point method where 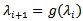 get;
get;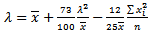 | (17) |
Using simple program, the moment estimator of 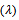 is obtained, therefore;
is obtained, therefore; 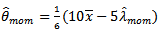 | (18) |
From 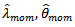 we can estimate
we can estimate 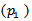 by moment estimator from solving;
by moment estimator from solving;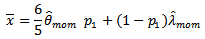 And from equation (8) since;
And from equation (8) since;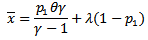 Use
Use 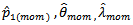 to obtain
to obtain 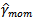
3. Maximum Likelihood Method[5]
To apply the ML for the mixture distribution 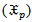 from two subpopulation (
from two subpopulation (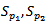 ), where (
), where (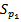 ) is Pareto population and
) is Pareto population and 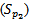 is Weibull population and we assume
is Weibull population and we assume 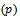 is mixing proportion parameters, where
is mixing proportion parameters, where 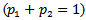 . Let
. Let 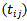 is the time failure for random sample
is the time failure for random sample 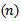 taken from mixed distribution
taken from mixed distribution 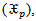 if we can determine the units of each sub population
if we can determine the units of each sub population 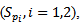 then choosing the random variable
then choosing the random variable 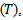 which is the time through it the failure time of
which is the time through it the failure time of 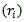 units can be determined before
units can be determined before 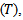
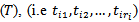 such that;
such that;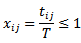 Therefore the sample units are of type (time censored sampling Type 1) and the conditional function for time failure from
Therefore the sample units are of type (time censored sampling Type 1) and the conditional function for time failure from 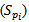 for units that failed before time
for units that failed before time 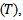 is;
is;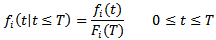 The probability that
The probability that 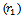 unit from
unit from 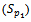 failed before
failed before 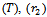 unit from
unit from 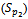 failed before
failed before 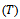 also, and
also, and 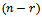 is remained until time
is remained until time 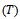 , is;
, is;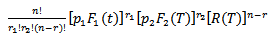 | (9) |
Then the likelihood function for sample is;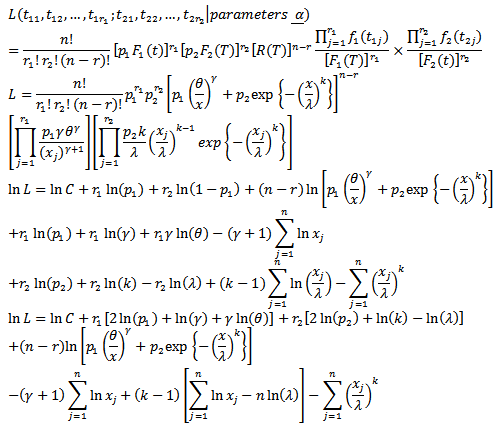 The parameters here are
The parameters here are 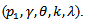
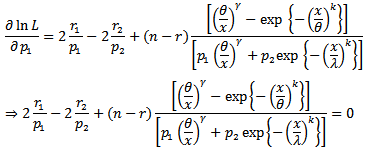 Therefore;
Therefore; 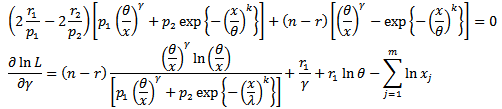
4. Simulation Procedure
We have;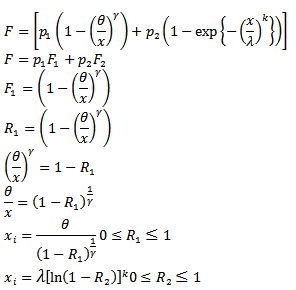 To find the estimators of (MOM & MLE), we perform simulation experiments using Monte Carlo assuming that;
To find the estimators of (MOM & MLE), we perform simulation experiments using Monte Carlo assuming that; Chosen values of parameters are;
Chosen values of parameters are;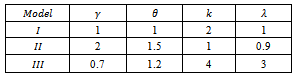 Also chosen values for predetermined censoring time (T).
Also chosen values for predetermined censoring time (T).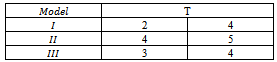 Also the total number of time intervals
Also the total number of time intervals 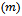 are;
are; The results for estimators of parameters are explained in the following tables;
The results for estimators of parameters are explained in the following tables;Table (1). Values of (MLE) estimatorsfor parameters of
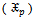 distribution for model I, (L=1000) distribution for model I, (L=1000)
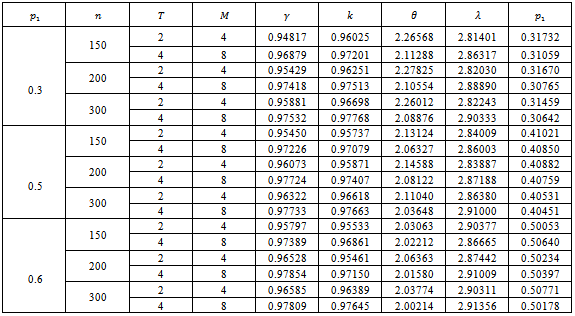 |
| |
|
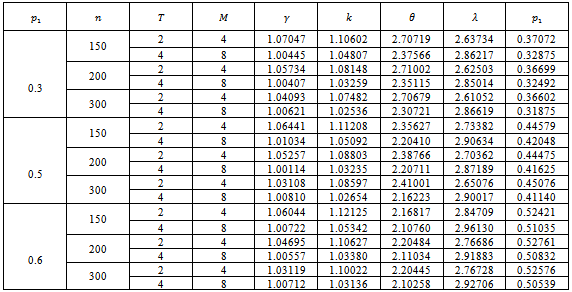
Table (2). Values of (MOM) estimatorsfor parameters of
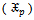 distribution for model I, (L=1000) distribution for model I, (L=1000)
 |
| |
|
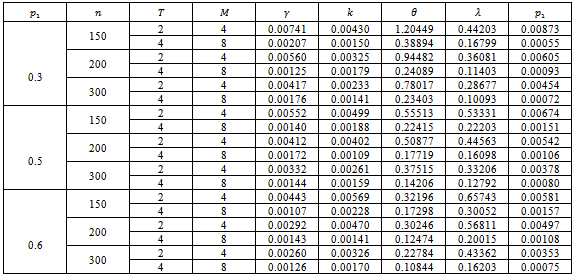
Table (3). Values of MSE for MLE estimators of
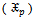 distribution for model I, (L=1000) distribution for model I, (L=1000)
 |
| |
|
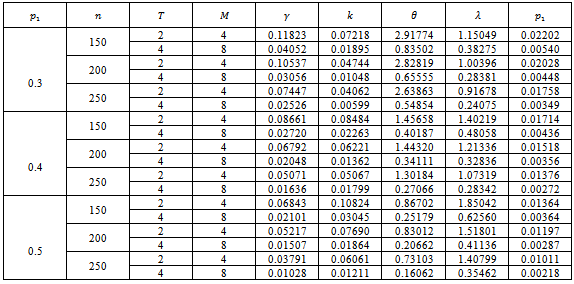
Table (4). Values of MSE for MOMestimators of
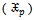 distribution for model I, (L=1000) distribution for model I, (L=1000)
 |
| |
|
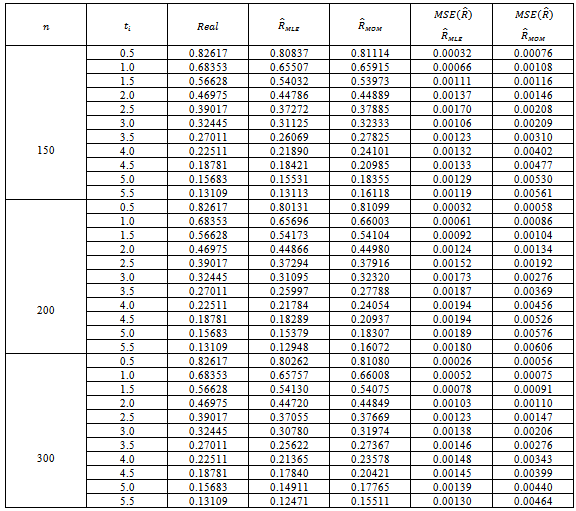
Table (5). Values of reliability function estimator by MLE , MOM & MSE
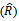 for model I for model I
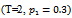
 |
| |
|
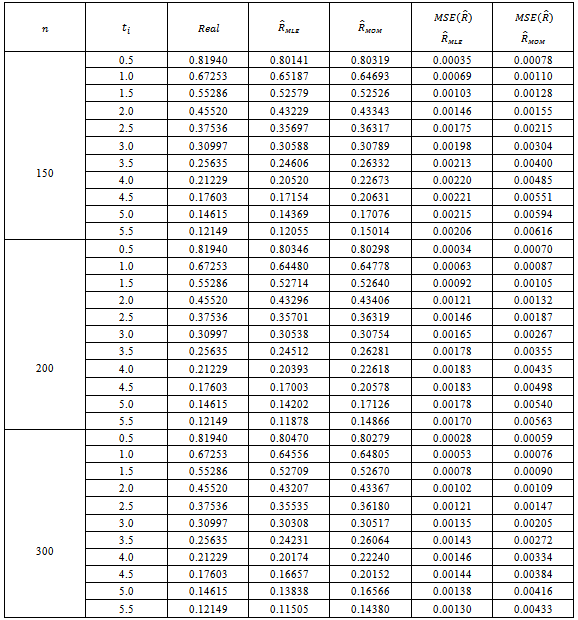
Table (6). Values of reliability function estimator by MLE, MOM & MSE
 for model I for model I
 |
| |
|
Table (7). Values of reliability function estimator by MLE , MOM & MSE
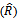 for model I for model I
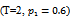
 |
| |
|
5. Conclusions
From simulation experiments, the results indicate that:1-The maximum likelihood estimator for reliability function is better than the moment estimator of reliability function.2- When 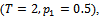 the values of estimator
the values of estimator 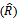 by MLE and MOM, and also of MSE
by MLE and MOM, and also of MSE 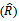 , are convergent inspite of increasing sample size.3- The estimator of
, are convergent inspite of increasing sample size.3- The estimator of 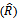 by MLE, and MOM approximated from real values of R by increasing the size of sample
by MLE, and MOM approximated from real values of R by increasing the size of sample 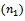 from
from 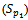 .4- The values of real function (R) are increasing with (T).5- The values of mean square errors for estimated parameters are decreased when (T) increasing, this is due to decreasing to failure for units drawn from each sub – population.
.4- The values of real function (R) are increasing with (T).5- The values of mean square errors for estimated parameters are decreased when (T) increasing, this is due to decreasing to failure for units drawn from each sub – population.
References
| [1] | Demidenko, E., 2004. Mixed Models: Theory and applications.Wiley, New Jersey. |
| [2] | Forbes C. E. M. N. & P.B., (2011), "Statistical Distribution" Canda. |
| [3] | Hanaa H. Abu-Zinadah, (2010), "A Study on Mixture of Exponentiated Pareto and Exponential Distributions" Journal of Applied Sciences Research, 6(4): 358-376, 2010 |
| [4] | Jiang, R., Murthy, D.N.P., Ji, P., 2001. Models involving two InverseWeibulldistributions.Reliab.Eng. Sys.Safet. 73 (1), 73–81. |
| [5] | K. Krishnamoorthy, Y. Lin, Y. P. Xia, (2009), " Confidence limits and prediction limits for a Weibull distribution based on the generalized variable approach"[Quick Edit] [CiTO] Journal of Statistical Planning and Inference, Vol. 139, No. 8. (Aug 2009), pp. 2675-2684, doi:10.1016/j.jspi.2008.12.010. |
| [6] | Maclachlan, G., Peel, D., 2000. Finite Mixture Models.Wiley, NewYork. |
| [7] | Mahir, and Ali, (2009), " Comparing two Weibull distributions using a mixing parameter", European Journal of Scientific Research. Vol.31, No.2, pp.296 – 305. |
| [8] | McCulloch, C.E. and S.R. Searle, 2001. Generalized, Linear, and Mixed Models. Wiley, New York. |
| [9] | Michel J. M., M. K. and R. P.(2004), " Bayesian Modeling and Inference on Mixtures of Distributions. |
| [10] | Mosler, K. and Scheicher, C. (2004), "Homogeneity testing in a Weibull mixture model", wiso.fak / wisostatsem / publications / Htiawmm / www.uni.koeln de / wmlx.pdf. |
| [11] | Mubarak, M. (2011), " Mixture if two Frechet Distributions: Properties and estimation", International Journal of Engineering Science and Technology (IJEST), Vol.3, No. 5, 4067 – 4073. |
| [12] | Nagode M, Fajdiga M (2006). “An Alternative Perspective on the Mixture Estimation Problem.”Reliability Engineering & System Safety, 91, 388–397. |
| [13] | Seidel,W., Mosler, K., Alker, M., 2000. A cautionary note on likelihood ratio tests in mixture models. Ann. Inst. Statist.Math. 52, 481–487. |
| [14] | Sultan, K. S., Ismail, M. A. Al-Moisheer, A. S. (2007), " Mixture of two inverse WeibullDistributions:Properties and estimation", Computational Statistics and Data Analysis, 51, 5377 – 5387. |
| [15] | Touw AE (2009). “Bayesian Estimation of MixedWeibullDistributions.”ReliabilityEngi- neering& System Safety, 94, 463–473. |
| [16] | Tsionas, E. G. (2002), "Bayesian analysis of finite mixtures of Weibull distributions", Commu. Stat. theory method, Vol. 31, No. 1, pp. 37 – 48. |
| [17] | Z. Yang, M. Xie, A. C. M. Wong, (2007), " A unified confidence interval for reliability-related quantities of two - parameter Weibull distribution" [Quick Edit] [CiTO]Journal of Statistical Computation and Simulation, Vol. 77, No. 5, pp. 365-378, doi:10.1080/00949650701227452. |
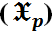

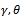 ) with Wiebull (two Parameters
) with Wiebull (two Parameters 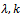 ), using mixing proportion
), using mixing proportion 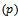 . The researcher construct the probability density function, and cumulative distribution function, reliability, hazard functions, moments are obtained the parameters which estimated by moment method (MOM) and maximum likelihood method (MLE) using simulation procedure taking different sample size
. The researcher construct the probability density function, and cumulative distribution function, reliability, hazard functions, moments are obtained the parameters which estimated by moment method (MOM) and maximum likelihood method (MLE) using simulation procedure taking different sample size 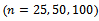 and replicate
and replicate 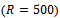 for each experiment.The comparison has been done through mean squares error (MSE).
for each experiment.The comparison has been done through mean squares error (MSE).
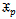 ), Pareto and Weibull, Moment Estimators, Maximum Likelihood Estimators, Mean Squares Error, Reliability
), Pareto and Weibull, Moment Estimators, Maximum Likelihood Estimators, Mean Squares Error, Reliability
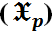 , American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 204-212. doi: 10.5923/j.ajms.20130304.04.
, American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 204-212. doi: 10.5923/j.ajms.20130304.04.
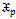 ), mixture of two parameters Pareto and two parameters Weibull.
), mixture of two parameters Pareto and two parameters Weibull.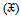 distribution is a mixture of some distributions with Weibull distribution, like exponential Weibull, Pareto Weibull, ErlangWeibull, Gamma Weibull. Now we explain
distribution is a mixture of some distributions with Weibull distribution, like exponential Weibull, Pareto Weibull, ErlangWeibull, Gamma Weibull. Now we explain 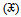 distribution which is a mixture of Pareto distribution with Weibull distribution and we shall denoted it by
distribution which is a mixture of Pareto distribution with Weibull distribution and we shall denoted it by 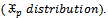 The statistical properties of (
The statistical properties of (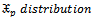 ) are explained, then we want to estimate its parameters;a. The probability density function
) are explained, then we want to estimate its parameters;a. The probability density function 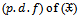 is;
is;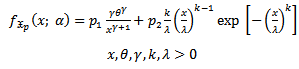
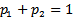 ) parameters of
) parameters of 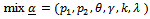 vector of parameters.b. The cumulative distribution function
vector of parameters.b. The cumulative distribution function 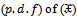 is;
is;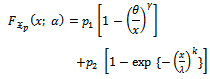
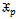 ) distribution denoted by;
) distribution denoted by; 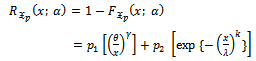
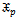 ) is;
) is;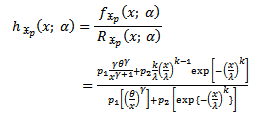
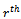 moment about origin of (
moment about origin of (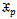 ) distribution which can be used in estimation method are defined as;
) distribution which can be used in estimation method are defined as;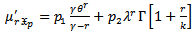
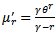 existing only for
existing only for 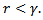 The mean and variance of (
The mean and variance of (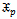 ) distribution can be obtained from (5), where;
) distribution can be obtained from (5), where;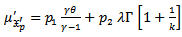
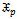 ) is;
) is;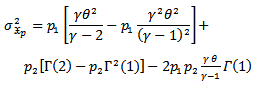
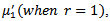 and another four moments.
and another four moments.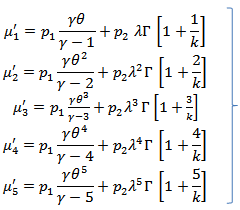
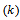 is integer
is integer 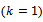 for example then solving these equations yield moment estimator.
for example then solving these equations yield moment estimator.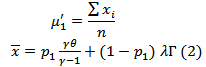
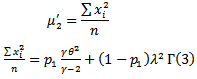
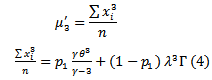
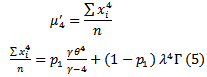
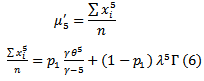
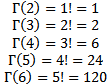 Here we assumed
Here we assumed  if we assume
if we assume 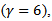 the parameters reduced to
the parameters reduced to 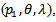 since
since 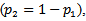 so we construct three equations for moment methods;
so we construct three equations for moment methods;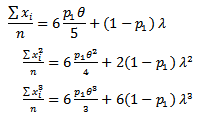 Assume
Assume 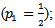
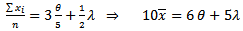
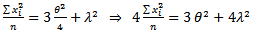
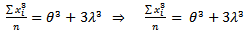
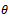 If
If 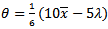 , substitute in (15);
, substitute in (15);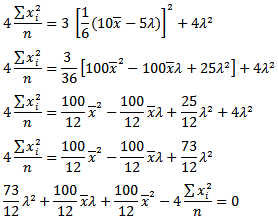 By using fixed point method where
By using fixed point method where 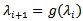 get;
get;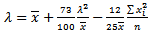
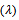 is obtained, therefore;
is obtained, therefore; 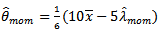
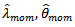 we can estimate
we can estimate 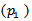 by moment estimator from solving;
by moment estimator from solving;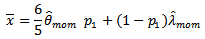 And from equation (8) since;
And from equation (8) since;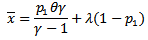 Use
Use 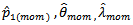 to obtain
to obtain 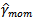
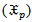 from two subpopulation (
from two subpopulation (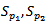 ), where (
), where (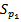 ) is Pareto population and
) is Pareto population and 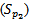 is Weibull population and we assume
is Weibull population and we assume 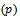 is mixing proportion parameters, where
is mixing proportion parameters, where 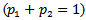 . Let
. Let 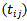 is the time failure for random sample
is the time failure for random sample 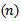 taken from mixed distribution
taken from mixed distribution 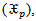 if we can determine the units of each sub population
if we can determine the units of each sub population 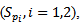 then choosing the random variable
then choosing the random variable 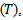 which is the time through it the failure time of
which is the time through it the failure time of 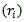 units can be determined before
units can be determined before 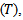
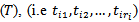 such that;
such that;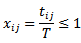 Therefore the sample units are of type (time censored sampling Type 1) and the conditional function for time failure from
Therefore the sample units are of type (time censored sampling Type 1) and the conditional function for time failure from 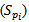 for units that failed before time
for units that failed before time 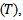 is;
is;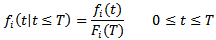 The probability that
The probability that 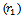 unit from
unit from 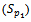 failed before
failed before 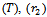 unit from
unit from 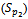 failed before
failed before 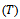 also, and
also, and 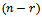 is remained until time
is remained until time 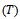 , is;
, is;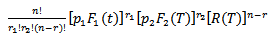
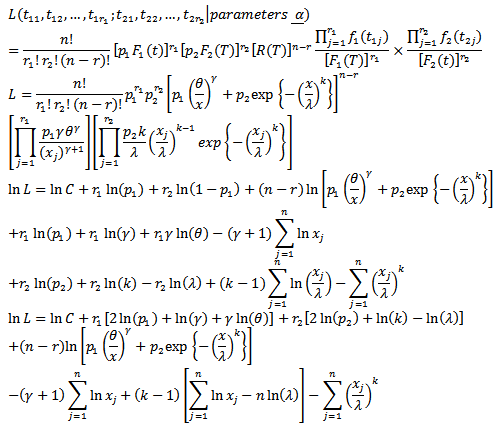 The parameters here are
The parameters here are 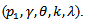
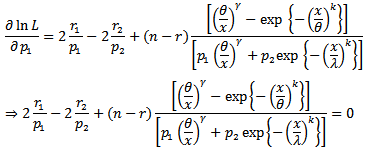 Therefore;
Therefore; 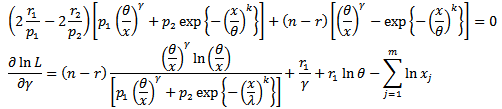
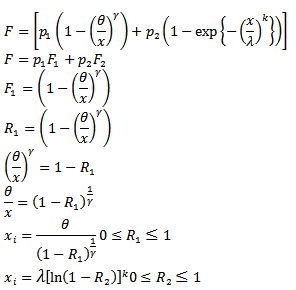 To find the estimators of (MOM & MLE), we perform simulation experiments using Monte Carlo assuming that;
To find the estimators of (MOM & MLE), we perform simulation experiments using Monte Carlo assuming that; Chosen values of parameters are;
Chosen values of parameters are; Also chosen values for predetermined censoring time (T).
Also chosen values for predetermined censoring time (T). Also the total number of time intervals
Also the total number of time intervals 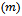 are;
are; The results for estimators of parameters are explained in the following tables;
The results for estimators of parameters are explained in the following tables;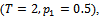 the values of estimator
the values of estimator 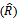 by MLE and MOM, and also of MSE
by MLE and MOM, and also of MSE 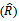 , are convergent inspite of increasing sample size.3- The estimator of
, are convergent inspite of increasing sample size.3- The estimator of 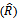 by MLE, and MOM approximated from real values of R by increasing the size of sample
by MLE, and MOM approximated from real values of R by increasing the size of sample 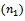 from
from 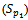 .4- The values of real function (R) are increasing with (T).5- The values of mean square errors for estimated parameters are decreased when (T) increasing, this is due to decreasing to failure for units drawn from each sub – population.
.4- The values of real function (R) are increasing with (T).5- The values of mean square errors for estimated parameters are decreased when (T) increasing, this is due to decreasing to failure for units drawn from each sub – population. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML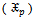 distribution for model I, (L=1000)
distribution for model I, (L=1000) 
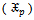 distribution for model I, (L=1000)
distribution for model I, (L=1000) 
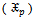 distribution for model I, (L=1000)
distribution for model I, (L=1000) 
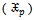 distribution for model I, (L=1000)
distribution for model I, (L=1000) 
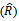 for model I
for model I 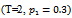

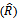 for model I
for model I 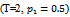

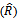 for model I
for model I