1. Introduction

The Banach contraction principle is one of the most important results in the metric fixed point theory. Theorems related to existence and uniqueness of fixed points are known as fixed point theorems. The theory of fixed points has become an important tool in non linear functional analysis since 1930. The significance of this field lies in its vast applicability to many branches of mathematics and other sciences. The study of common fixed points of mappings satisfying different contractive conditions has been explored extensively by many mathematicians ([1],[3],[5] &[6]). Recently, the fixed point theorem involving the concept of altering distance functions has become more popular and widely used by many researchers ([7] -[21]).

Iseki[6], Babu, G.R.V. et al.[2] had established an interesting result on unique common fixed point for sequence of mappings by using altering distances. It has been noticed that the right hand side of the condition for altering distances involved many complex functions of the metric d. Moreover, while showing the sequence obtained by iterations is Cauchy, these functions are very much difficult to handle from computation point of view.

It may be interesting to know that only one simple function involving the metric d is enough to establish the same assertion. In addition, the free parameter, which we have introduced in the contraction of condition, plays crucial role in covering several other results with specific different choices.

This flexibility of the condition may lead to some significant simple applications of the result to differential equations.

2. Preliminaries

In order to establish the main result, we require the following definitions and results are required:

Definition 2.1 Let (X, d) be a metric space. A mapping T: 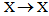is called a contraction mapping if there exists a real number k, 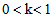, such that

d (Tx, Ty) 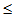kd (x, y), for all x, y in X.

The well-known Banach contraction theorem is given below:

“If T is a mapping of a complete metric space X into itself such that d(Tx,Ty) 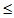k d(x,y), for all

x, yX and 0 < k <1. Then T has a unique fixed point.”

Definition 2.2 A function 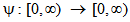is called a subadditive altering distance function if the following properties are satisfied:

(i) 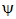is a continuous function

(ii) 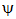is a monotonically increasing function

(iii)

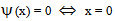(iv)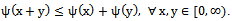

Lemma 2.1 (Lemma 1.3 of[14]). Let (M, d) be a metric space. Let {x_n} be a sequence in M such that 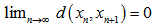. If {x_n} is not a Cauchy sequence in M, then there exists an 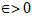for which, the subsequences 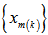and 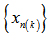of {x_n} may be obtained with m(k) > n(k) > k such that 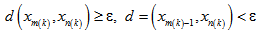and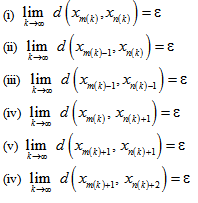

3. Results Already Proved

In 1974, Iseki (cf.[6]) established the following result:

Theorem 3.1 (Theorem 4.3 of[11]). Let (X, d) be a complete metric space and be a sequence of self maps of X. Suppose there are non-negative real numbers 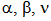such that for any x, y in X and i, j = 1, 2,…, n…

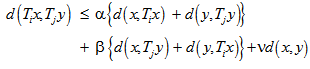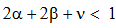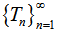where  Then has a unique fixed point.

Sastry et al.[20] have initiated the following Theorem in 1999:

Theorem 3.2 (Theorem 4.2 of[11]). Let (X, d) be a bounded complete metric space. Suppose 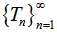is a sequence of self maps of X such that

T_iT_j = T_j T_i, for all i, j = 1, 2,…, n,…and satisfies the inequality:

There exists k 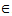(0, 1) and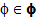

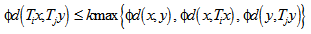Then, the sequence 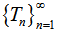has a unique common fixed point.

Babu et al.[2] had proved the following result in 2001:

Theorem 3.3 (Theorem 4.5 of[11]). Let (X, d) be a complete metric space and 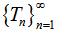be a sequence of self maps of X. Suppose there is a 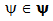satisfying the following inequality:

There exists k 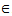[0, 1) such that

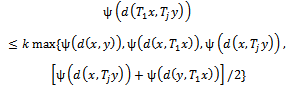for all x, y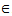X and for all j = 1, 2,…n,…. Then the mappings 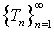have a unique common fixed point in X.

4. Main Result

Theorem 4.1 Let 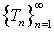be a sequence of self maps on a complete metric space (X, d) and 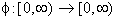be an altering distance function satisfying the condition:

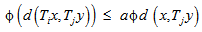(4.1)

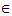for all i, j = 1,2,…,n,… and for all distinct x , y X, where 0 < a < ½ .

Then 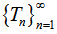has a unique common fixed point in X.

Remark 4.1 It may be noted that any specific choice of parameter ‘a’ should be bounded by 0 and ½.

Proof. Let x be an arbitrary point in X and {x_n} be a sequence of points of X. Consider

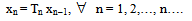(4.2)

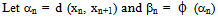(4.3)

Then

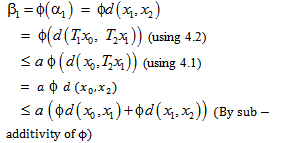This implies that

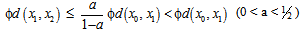Hence 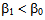. Thus, by induction, it follows

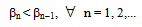This implies that 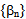is decreasing sequence of non-negative real numbers; hence, it converges to zero,

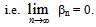Since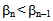

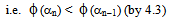This implies that the sequence {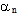} is also a deceasing sequence of non-negative real number and hence 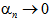as .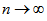

Claim: The sequence {x_n} is a Cauchy sequence.

For this, it is sufficient to show that the subsequence {x_2n} of {x_n} is a Cauchy sequence, Let, if possible, {x_2n} is not a Cauchy sequence, then there exists an 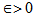and monotonically increasing sequence of natural numbers {2m(k)} and {2n(k)} such that n(k) > m(k) ,

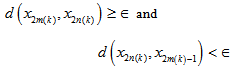(4.4)

In view of (4.4), it is noted that

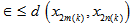This implies that

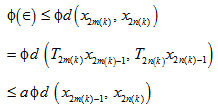Letting 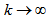, yields

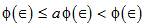(using lemma 2.1)

which is a contradiction. Hence, {x_2n} is a Cauchy sequence therefore {x_n} is a Cauchy sequence in X. Since X is complete metric space, therefore {x_n} converges to a point x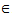X.

Claim: x is a common fixed point of sequence of mappings .

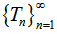Consider

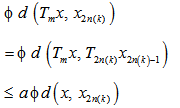Applying limit as 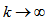, we get

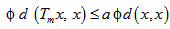This implies that

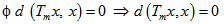i.e. T_mx = x, for all m = 1, 2,…

This show that x is fixed point of T_m, 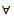m = 1, 2,…

Thus, x is a common fixed point of the sequence of mappings .

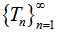Claim: x is unique.

Let, if possible, 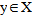such that y is also a fixed point of T_n, for all n=1, 2,…

i.e. T_ny = y, for all n =1, 2, …

Now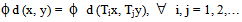

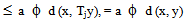This implies that

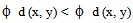which is a contradiction. Thus, x is unique common fixed point of sequence of mappings .

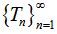5. Conclusions

By considering d 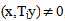, the following may be noted :

(i) Putting 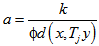and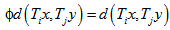

where

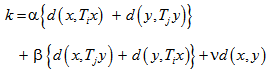and 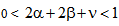in (4.1) leads to the Theorem 4.3 of[11].

(ii) Putting

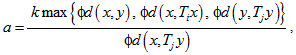where 0 < k < 1 in (4.1) yields Theorem 4.2 of [11].

(iii) Putting 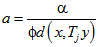, where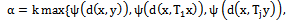

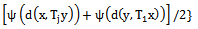and 0 < k < 1 in (4.1) Theorem 4.5 of[11] can obtained.

Note: (ii) and (iii) hold without sub-additive condition on .

ACKNOWLEDGEMENTS

Authors would like to thank referees of this paper for their valuable suggestions.