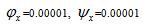Rajesh C. Shah1, M. M. Parsania2
1Department of Applied Mathematics, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara – 390 001, Gujarat State, India
2Department of Mathematics, School of Engineering, R.K. University, Rajkot, Gujarat State, India
Correspondence to: Rajesh C. Shah, Department of Applied Mathematics, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara – 390 001, Gujarat State, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The aim of the present paper is to make a comparative study of magnetic fluid lubricated various designed slider bearings ( that is, slider bearings having inclined pad stator, exponential pad stator, secant pad stator, convex pad stator) with that of slider bearing having parallel pad stator including effects of porosity, slip velocity at both the ends and squeeze velocity (which appear when the upper plate approach to lower one) under the magnetic field oblique to the lower plate ( pad or surface ). The paper also studied about the cases of anisotropic permeability and isotropic permeability with respect to both upper and lower porous matrix (layer). The dimensionless load carrying capacity for porous matrixes of various sizes attached at upper and lower plates is calculated for various slider bearings and compared with slider bearing having parallel pad stator. From the results and discussion, it is suggested to have slider bearing design with inclined or convex pad stator surfaces and occasionally secant pad stator surface.
Keywords:
Magnetic Fluid, Porosity, Slider Bearings, Permeability
Cite this paper: Rajesh C. Shah, M. M. Parsania, Comparative Study of Parallel Plate Slider Bearing with Other Slider Bearings Using Magnetic Fluid as Lubricant, American Journal of Mathematics and Statistics, Vol. 3 No. 4, 2013, pp. 179-189. doi: 10.5923/j.ajms.20130304.01.
1. Introduction
Magnetic fluid or Ferrofluid[1] are stable colloidalsuspensions containing fine ferromagnetic particles dispersing in a liquid, called carrier liquid, in which a surfactant is added to generate a coating layer preventing the flocculation of the particles. When an external magnetic field is applied, magnetic fluids experience magnetic body forces depends upon the magnetization of ferromagnetic particles. Owing to these features magnetic fluids are useful in many applications like sensors, centrifugal switches, dampers, etc.[2].With the advent of magnetic fluid, many authors have worked on magnetic fluid lubrication from different viewpoints, of which some references are as follows:Tipei[3] studied on theory of lubrication with ferrofluids and applied it to short bearings. Agrawal[4] studied magnetic fluid effects on a porous inclined bearing and found that the magnetization of the magnetic particles in the lubricant increased its load capacity without affecting the friction on the moving slider. Sinha et. al.[5] studied ferrofluid lubrication of cylindrical rollers with cavitations. Ram and Verma[6] studied on ferrofluid lubrication in porous inclined slider bearing. Shah and Bhat in[7,8] studied respectively on ferrofluid lubrication of porous slider bearing with velocity slip, and ferrofluid squeeze film between curved annular plates including rotation of magnetic particles. Ahmad and Singh[9] studied on magnetic fluid lubrication of porous-pivoted slider bearing with slip velocity. Recently, Shah and Patel[10] studied on mathematical Modeling of newly designed ferrofluid based slider bearing including effects of porosity, anisotropic permeability, slip velocity at both the ends, and squeeze velocity.With the motivation that, the porous layer in the bearing is considered because of its advantageous property of self lubrication, the present paper presents comparative study of magnetic fluid lubricated various designed slider bearings (that is, slider bearings having inclined pad stator, exponential pad stator, secant pad stator, convex pad stator) with that of slider bearing having parallel pad stator including effects of porosity, slip velocity at both the ends and squeeze velocity (which appear when the upper plate approach to lower one) under the magnetic field oblique to the lower plate. A magnetic fluid lubrication equation is derived for the above problem in general and the various sizes of porous matrix are attached to upper and lower plates considered for computation of dimensionless load carrying capacity. Also, it is computed for two different cases of anisotropic permeability and isotropic permeability with respect to both upper and lower porous matrix. The magnetic fluid flow model considered here is due to R. E. Rosensweig[1] and magnetic fluids used in the computations are of water based.
2. Derivation of the Mathematical Model
Figure 1-5 shows schematic diagram of various system of slider bearings under study which consists of a magnetic fluid film of thickness h within a stator pad surface of various shapes and a slider of length A in the x-direction and width B in y-direction, A<< B. The value of h is h2 at the inlet and h1 at the outlet. The expression for film thicknesses h are shown against their bearing design as follows:(a) For slider bearing having inclined pad stator: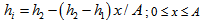 | (1) |
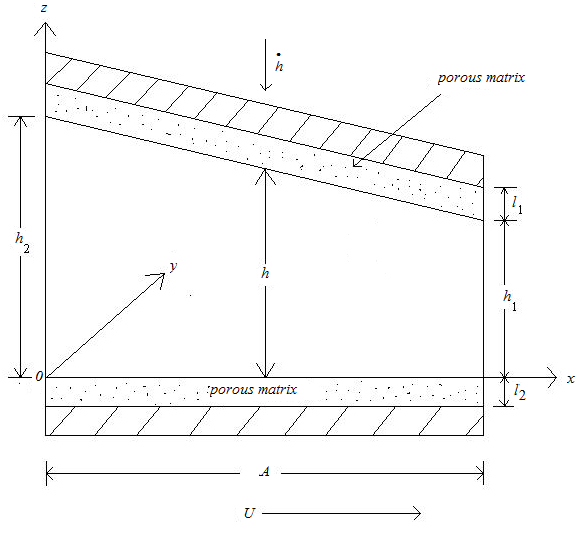 | Figure 1. Slider bearing having inclined pad stator |
(b) For slider bearing having exponential pad stator: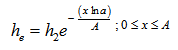 | (2) |
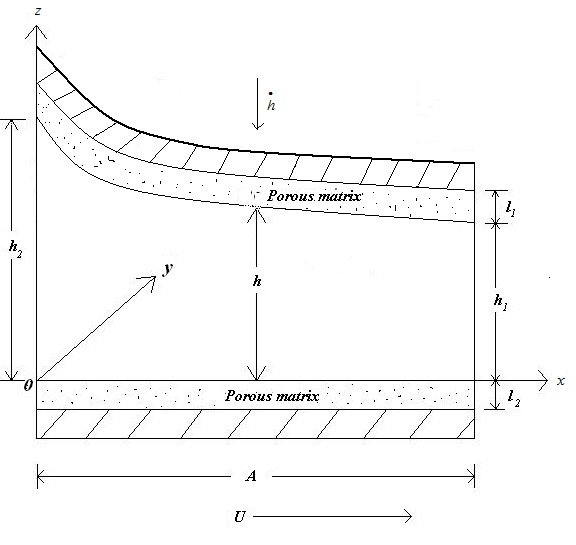 | Figure 2. Slider bearing having exponential pad stator |
(c) For slider bearing having secant pad stator: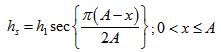 | (3) |
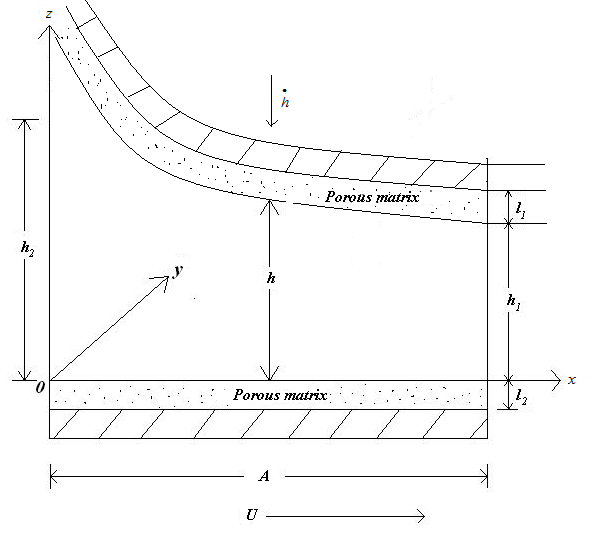 | Figure 3. Slider bearing having secant pad stator |
(d) For slider bearing having convex pad stator: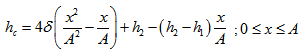 | (4) |
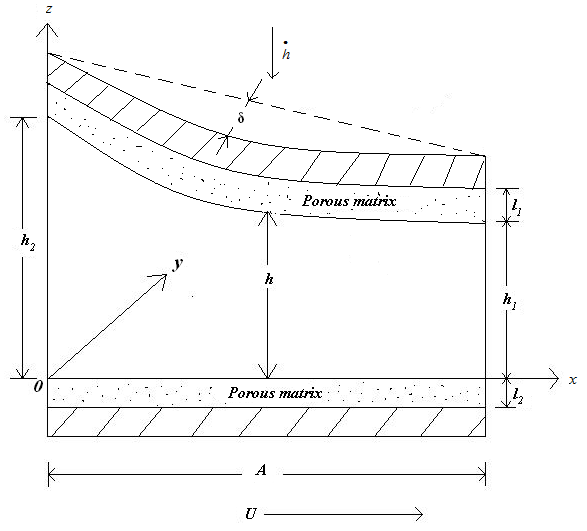 | Figure 4. Slider bearing having convex pad stator |
where δ is the central thickness of the convex pad.(e) For slider bearing having parallel pad stator: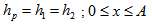 | (5) |
Porous matrix of thickness l2 and l1 metres have attached with the slider and stator respectively. Both the porous matrix are backed by a solid wall. The slider moves with a uniform velocity U in the x-direction. Also, stator moves normally towards the slider with a uniform velocity ( known as squeeze velocity ) 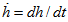 , where t is time in seconds.
, where t is time in seconds.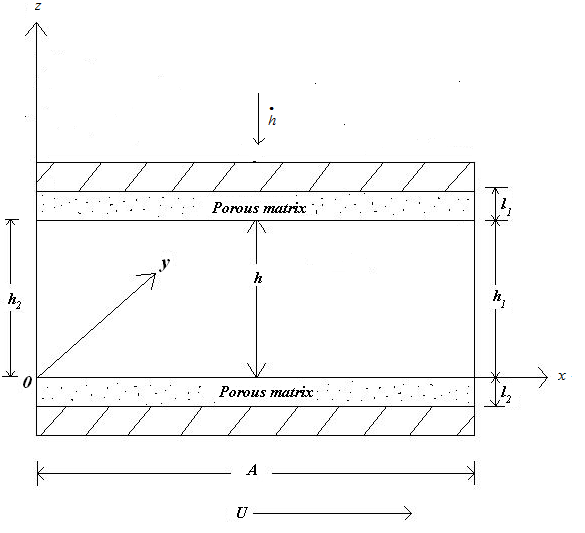 | Figure 5. Slider bearing having parallel pad stator |
(1) Following[10,11] , the basic equations governing the magnetic fluid flow based on R. E. Rosensweig model are given as follows: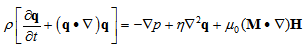 | (6) |
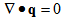 | (7) |
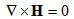 | (8) |
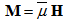 | (9) |
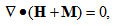 | (10) |
where 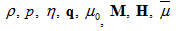 are density, film pressure, fluid viscosity, fluid velocity, free space permeability, the magnetization vector, magnetic field vector and magnetic susceptibility respectively.By combining above equations (6) to (10) under the usual assumption of lubrication, neglecting inertia terms and that the derivatives of velocities across the film predominate, one - dimensional equation governing the lubricant flow in the film region yields
are density, film pressure, fluid viscosity, fluid velocity, free space permeability, the magnetization vector, magnetic field vector and magnetic susceptibility respectively.By combining above equations (6) to (10) under the usual assumption of lubrication, neglecting inertia terms and that the derivatives of velocities across the film predominate, one - dimensional equation governing the lubricant flow in the film region yields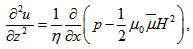 | (11) |
where u is the film fluid velocity in the x-direction and H is the magnetic field strength.(2)The integral form of continuity equation in the film region is given by 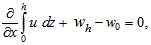 | (12) |
where w is the axial component of the fluid velocity in the film.(3) Using Darcy’s law, the velocity components of the fluid in the porous matrix are given as follow:For upper porous region: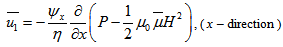 | (13) |
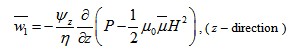 | (14) |
where 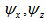 are fluid permeabilities in the upper porous region in x and z directions respectively, and P is the fluid pressure in the porous region.For lower porous region:
are fluid permeabilities in the upper porous region in x and z directions respectively, and P is the fluid pressure in the porous region.For lower porous region: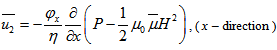 | (15) |
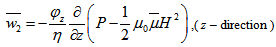 | (16) |
where 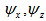 are fluid permeabilities in the lower porous region in x and z directions respectively, and P is the fluid pressure in the porous region.(4)The continuity equation in the porous regions are given as follows:For upper porous region:
are fluid permeabilities in the lower porous region in x and z directions respectively, and P is the fluid pressure in the porous region.(4)The continuity equation in the porous regions are given as follows:For upper porous region: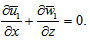 | (17) |
For lower porous region: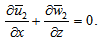 | (18) |
Case 1 For Anisotropic permeabilitySolving equation (11) under the slip boundary conditions given by Sparrow et. al.[12] and modified by Shah and Bhat[13] with the addition of slider velocity U to[12]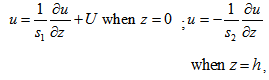 | (19) |
wherebeing slip parameter ; 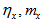 are porosities in the x- direction for lower and upper porous regions respectively, one obtain
are porosities in the x- direction for lower and upper porous regions respectively, one obtain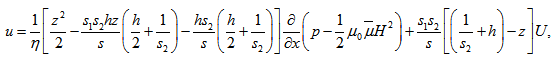 | (20) |
where Substituting the above value of u in the integral form of continuity equation (12), yields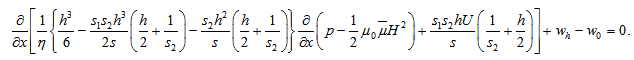 | (21) |
Substituting equations (13) and (14) in the continuity equation for upper porous region (17), and integrating with respect to z across the upper porous matrix ( h, h+l1 ), yields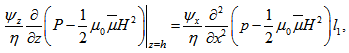 | (22) |
using Morgan-Cameron approximation[10] and the fact that surface 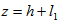 is non-porous.Substituting equations (15) and (16) in the continuity equation for lower porous region (18) and integrating with respect to z across the lower porous matrix (
is non-porous.Substituting equations (15) and (16) in the continuity equation for lower porous region (18) and integrating with respect to z across the lower porous matrix ( l2, 0 ), yields
l2, 0 ), yields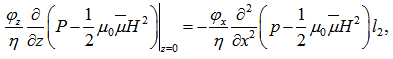 | (23) |
using Morgan-Cameron approximation[10] and the fact that surface 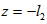 is non-porous.Considering the normal component of velocity across the film-porous interface are continuous, so that
is non-porous.Considering the normal component of velocity across the film-porous interface are continuous, so that 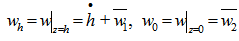 , using equations (14),(16),(21) and (22)-(23), one obtain
, using equations (14),(16),(21) and (22)-(23), one obtain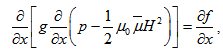 | (24) |
where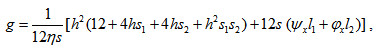
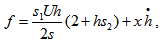 which is known as Reynolds’s type equation for the considered phenomenon.As mentioned earlier, here magnetic field is considered to be oblique to the lower plate and vanishing at the inlet and outlet of the bearing as
which is known as Reynolds’s type equation for the considered phenomenon.As mentioned earlier, here magnetic field is considered to be oblique to the lower plate and vanishing at the inlet and outlet of the bearing as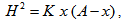 | (25) |
where K being a quantity chosen to suit the dimensions of both sides of equation (25). Introducing the dimensionless quantities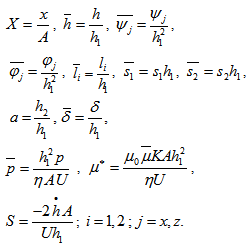 Then the dimensionless form of equations (1)-(5) and (24)-(25) becomes
Then the dimensionless form of equations (1)-(5) and (24)-(25) becomes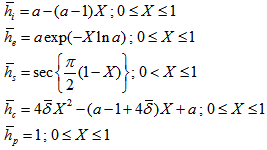 and
and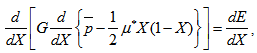 | (26) |
where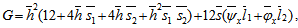 | (27) |
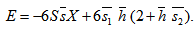 | (28) |
Also,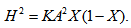 | (29) |
Equation (26) with (27)-(28) is known as dimensionless form of Reynolds’s equation for anisotropic permeable porous plate with respect to both upper and lower porous matrix. Case 2 For Isotropic permeabilityIn this case 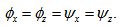 By following similar procedure as in Case 1, the following dimensionless form of Reynolds’s equation for isotropic permeable porous plate with respect to both upper and lower porous matrix is obtained. where
By following similar procedure as in Case 1, the following dimensionless form of Reynolds’s equation for isotropic permeable porous plate with respect to both upper and lower porous matrix is obtained. where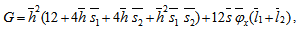 | (31) |
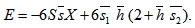 | (32) |
Equation (30) with (31)-(32) is known as dimensionless form of Reynolds’s equation for isotropic permeable porous plate with respect to both upper and lower porous matrix.
3. Calculation of Dimensionless Load Carrying Capacity
Since the pressure is negligible on the boundaries of the slider bearing compared to inside pressure, solving equation (26) under boundary conditions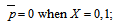 the dimensionless film pressure
the dimensionless film pressure 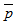 is obtained as follows:
is obtained as follows: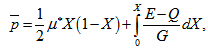 where
where 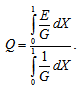 The load carrying capacity W is expressed in dimensionless form aswhere
The load carrying capacity W is expressed in dimensionless form aswhere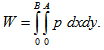 For anisotropic case G, E are given by equations (27)-(28), and for isotropic case G, E are given by equations (31)-(32).
For anisotropic case G, E are given by equations (27)-(28), and for isotropic case G, E are given by equations (31)-(32).
4. Calculation of Results
The dimensionless load carrying capacity (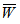 ) for various designed slider bearings ( that is, slider bearings having inclined pad stator, exponential pad stator, secant pad stator, convex pad stator, parallel pad stator ) are calculated for various sizes of upper and lower porous matrix using Simpson’s one third rule with step size 0.1, considering following values of the parameters :
) for various designed slider bearings ( that is, slider bearings having inclined pad stator, exponential pad stator, secant pad stator, convex pad stator, parallel pad stator ) are calculated for various sizes of upper and lower porous matrix using Simpson’s one third rule with step size 0.1, considering following values of the parameters :
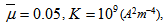
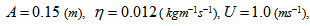
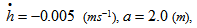
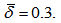 In the following cases, the notations used are
In the following cases, the notations used are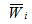 - Dimensionless load carrying capacity for slider bearing having inclined pad stator
- Dimensionless load carrying capacity for slider bearing having inclined pad stator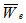 - Dimensionless load carrying capacity for slider bearing having exponential pad stator
- Dimensionless load carrying capacity for slider bearing having exponential pad stator 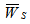 - Dimensionless load carrying capacity for slider bearing having secant pad stator
- Dimensionless load carrying capacity for slider bearing having secant pad stator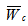 - Dimensionless load carrying capacity for slider bearing having convex pad stator
- Dimensionless load carrying capacity for slider bearing having convex pad stator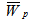 - Dimensionless load carrying capacity for slider bearing having parallel pad statorCase 1 For Anisotropic permeability
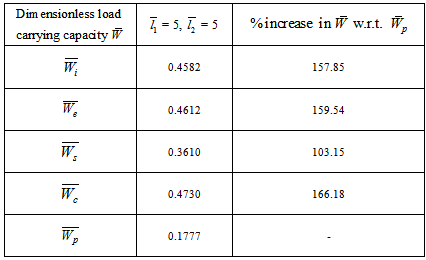
- Dimensionless load carrying capacity for slider bearing having parallel pad statorCase 1 For Anisotropic permeabilityTable 1. Values of
 |
| |
|
Case 2 For Isotropic permeability
5. Discussion of Results
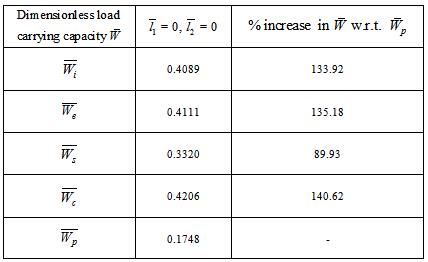
The mathematical study of water based magnetic fluid lubricated various designed slider bearing are discussed and compared for dimensionless load carrying capacity 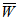 with slider bearing having parallel pad stator considering effects of porosity, slip velocity at both the ends, and squeeze velocity under an oblique magnetic field. The two cases of anisotropic permeability and isotropic permeability with respect to both upper and lower porous matrix are discussed for various sizes porous matrixes attached at both the plates. The following observations can be made from the results:(1) It is observed form tables 1-4 that maximum
with slider bearing having parallel pad stator considering effects of porosity, slip velocity at both the ends, and squeeze velocity under an oblique magnetic field. The two cases of anisotropic permeability and isotropic permeability with respect to both upper and lower porous matrix are discussed for various sizes porous matrixes attached at both the plates. The following observations can be made from the results:(1) It is observed form tables 1-4 that maximum 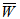 is obtained when
is obtained when 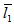 = 0 and
= 0 and 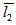 = 0. But with the insertation of porous layer at both the plates, maximum
= 0. But with the insertation of porous layer at both the plates, maximum 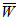 can be obtained when
can be obtained when 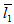 = 1 and
= 1 and 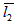 = 1. The almost same behaviour is obtained when
= 1. The almost same behaviour is obtained when 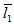 = 5 and
= 5 and 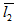 = 1; that is, when the porous layer attached to the upper plate (stator) is thick and porous layer attached to the lower plate (slider) is thin. But if we reverse the thickness of the porous plates; that is, when
= 1; that is, when the porous layer attached to the upper plate (stator) is thick and porous layer attached to the lower plate (slider) is thin. But if we reverse the thickness of the porous plates; that is, when 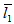 = 1 and
= 1 and 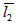 = 5 then the increase of
= 5 then the increase of 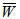 is substantially less. Moreover, the percentage increases in
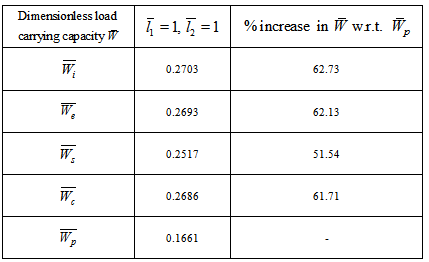
is substantially less. Moreover, the percentage increases in 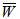 for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables. (2) It is observed form tables 5-8 that maximum
for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables. (2) It is observed form tables 5-8 that maximum 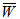 is obtained when
is obtained when 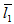 = 0 and
= 0 and 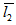 = 0 . But with the insertation of porous layer at both the plates, maximum
= 0 . But with the insertation of porous layer at both the plates, maximum 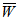 can be obtained when
can be obtained when 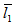 = 1 and
= 1 and 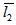 = 1. The almost same behaviour is obtained when
= 1. The almost same behaviour is obtained when 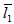 = 1 and
= 1 and 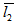 = 5; that is, when the porous layer attached to the lower plate (slider) is thick and porous layer attached to the upper plate (stator) is thin. But if we reverse the thickness of the porous plates; that is, when
= 5; that is, when the porous layer attached to the lower plate (slider) is thick and porous layer attached to the upper plate (stator) is thin. But if we reverse the thickness of the porous plates; that is, when 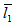 = 5 and
= 5 and 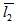 = 1 then the increase of
= 1 then the increase of 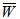 is substantially less. Moreover, the percentage increases in
is substantially less. Moreover, the percentage increases in 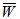 for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables.In summary, when the permeability of the upper porous layer is small as compared to lower porous layer, then
for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables.In summary, when the permeability of the upper porous layer is small as compared to lower porous layer, then 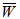 increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then
increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then 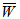 increases with the increase of thickness of lower porous layer.Thus, maximum
increases with the increase of thickness of lower porous layer.Thus, maximum 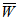 can be obtained when permeability decreases and thickness of the porous layer increases. It is observed form tables 9-11 that maximum
can be obtained when permeability decreases and thickness of the porous layer increases. It is observed form tables 9-11 that maximum 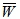 is obtained when
is obtained when 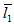 = 5 and
= 5 and 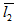 = 5 . Also,
= 5 . Also, 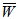 remains same whether
remains same whether 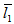 = 5 and
= 5 and 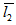 = 10 or
= 10 or 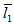 = 10 and
= 10 and 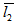 = 5. Similar type of behaviour for
= 5. Similar type of behaviour for 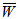 is obtained for tables 12-14. Moreover, for smaller values of permeabilities
is obtained for tables 12-14. Moreover, for smaller values of permeabilities 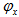 and
and 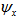 , better
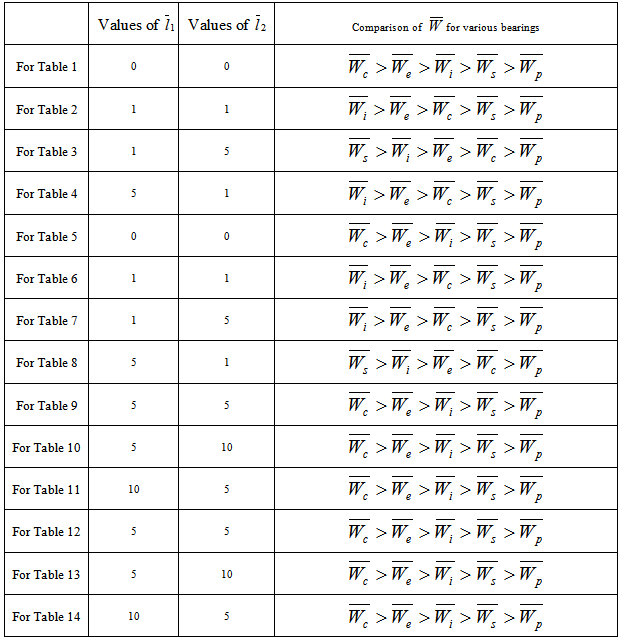
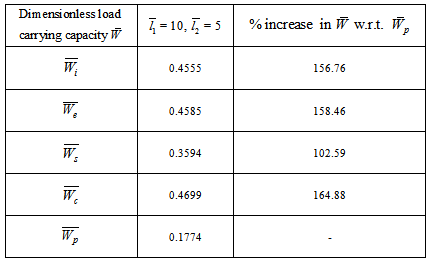
, better 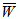 is obtained ( refer tables 9-11) as compared to larger values ( refer tables 12-14).The following table 15 indicates the comparison of
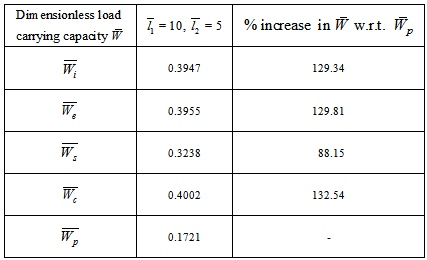
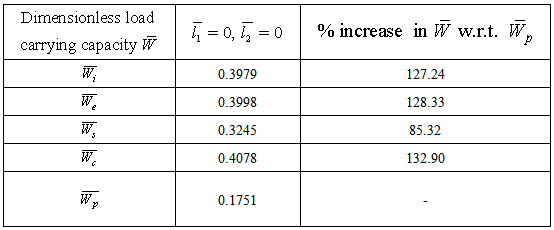
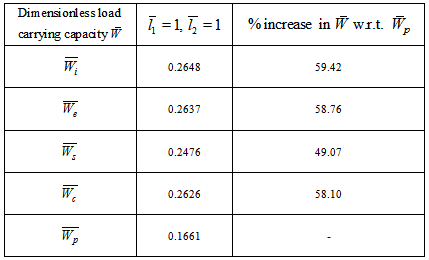
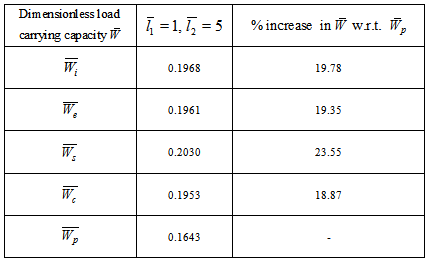
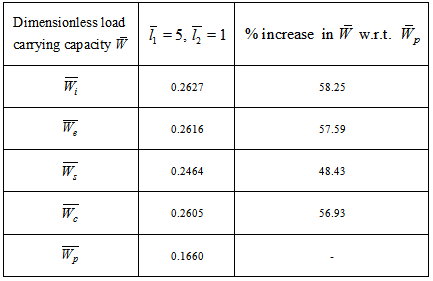
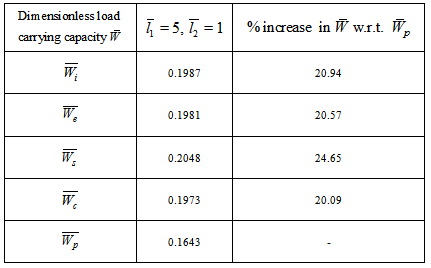
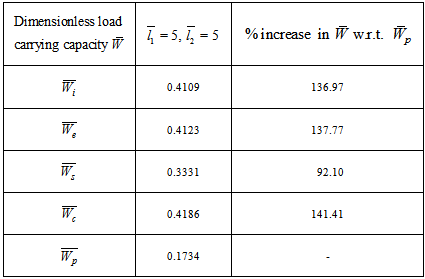
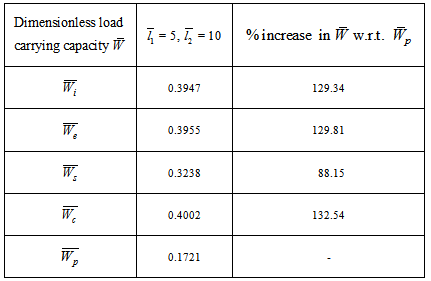
is obtained ( refer tables 9-11) as compared to larger values ( refer tables 12-14).The following table 15 indicates the comparison of 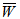 for various bearings.
for various bearings.Table 15. Comparison of dimensionless load carrying capacity for various bearings
 |
| |
|
6. Conclusions
Based upon the above formulation, and results & discussion the following conclusions can be drawn for designing slider bearing:(1) Because of having the self lubrication property of the porous plate bearing, it is suggested to have both the porous plate bearing for better self lubrication.(2) When the permeability of the upper porous layer is small as compared to lower porous layer, then 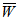 increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then
increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then 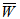 increases with the increase of thickness of lower porous layer.(3) For isotropic case more better
increases with the increase of thickness of lower porous layer.(3) For isotropic case more better 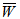 is obtained.(4) It should be noted that a constant magnetic field does not enhance
is obtained.(4) It should be noted that a constant magnetic field does not enhance 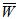 in this model since
in this model since 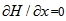 in equation (11).(5) It is observed form table 15 that the suggestive design of bearing is either inclined or convex pad stator surfaces and occasionally secant pad stator surface.
in equation (11).(5) It is observed form table 15 that the suggestive design of bearing is either inclined or convex pad stator surfaces and occasionally secant pad stator surface.
References
| [1] | Rosensweig R E. Ferrohydrodynamics. New York:Cambridge University Press;1985. |
| [2] | Mehta R V, Upadhyay R V. Science and Technology of ferrofluids. Current Science 1999; 76: 305-312. |
| [3] | Tipei N. Theory of Lubrication with Ferrofluids: Application to short bearings. Transactions of ASME 1982; 104: 510-515. |
| [4] | Agrawal V K. Magnetic fluid based porous inclined slider bearing. Wear 1986; 107: 133-139. |
| [5] | Sinha P, Chandra P, Kumar D. Ferrofluid lubrication of cylindrical rollers with cavitation. Acta Mechanica 1993; 98: 27-38. |
| [6] | Ram P and Verma P D S. Ferrofluid lubrication in porous inclined slider bearing. Indian Journal of Pure & Applied Mathematics 1999; 30(12): 1273-1281. |
| [7] | Shah R C, Bhat M V. Ferrofluid lubrication in porous slider bearing with velocity slip. International Journal of Mechanical Sciences 2002; 44: 2495-2502. |
| [8] | Shah R C, Bhat M V. Ferrofluid squeeze film between curved annular plates including rotation of magnetic particles. Journal of Engineering Mathematics 2005; 51: 317-324. |
| [9] | Ahmad N and Singh JP. Magnetic fluid lubrication of porous-pivoted slider bearing with slip velocity. Journal of Engineering Tribology 2007; 221: 609-613. |
| [10] | Shah R C, Patel D B. Mathematical Modeling of newly designed Ferrofluid Based Slider Bearing Including Effects of Porosity, Anisotropic Permeability, Slip Velocity at Both the Ends, and Squeeze Velocity. Applied Mathematics 2012; 2(5): 176-183. |
| [11] | Shah R C, Bhat M V. Analysis of a porous exponential slider bearing lubricated with a ferrofluid considering slip velocity. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2003; 25(3) : 264-267. |
| [12] | Sparrow E M, Beavers G S, Hwang I T. Effect of velocity slip on porous walled squeeze films. Journal of Lubrication Technology1972; 94: 260-265. |
| [13] | Shah R C, Bhat M V. Ferrofluid lubrication equation for porous bearing considering anisotropic permeability and slip velocity. Indian Journal of Engineering & Material Sciences 2003; 10 : 277-281. |

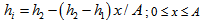

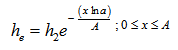

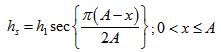

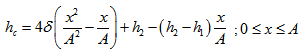

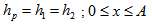
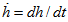 , where t is time in seconds.
, where t is time in seconds.
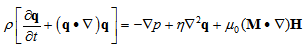
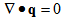
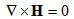
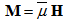
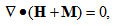
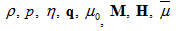 are density, film pressure, fluid viscosity, fluid velocity, free space permeability, the magnetization vector, magnetic field vector and magnetic susceptibility respectively.By combining above equations (6) to (10) under the usual assumption of lubrication, neglecting inertia terms and that the derivatives of velocities across the film predominate, one - dimensional equation governing the lubricant flow in the film region yields
are density, film pressure, fluid viscosity, fluid velocity, free space permeability, the magnetization vector, magnetic field vector and magnetic susceptibility respectively.By combining above equations (6) to (10) under the usual assumption of lubrication, neglecting inertia terms and that the derivatives of velocities across the film predominate, one - dimensional equation governing the lubricant flow in the film region yields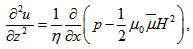
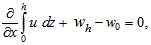
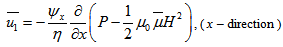
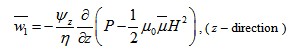
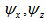 are fluid permeabilities in the upper porous region in x and z directions respectively, and P is the fluid pressure in the porous region.For lower porous region:
are fluid permeabilities in the upper porous region in x and z directions respectively, and P is the fluid pressure in the porous region.For lower porous region: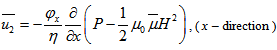
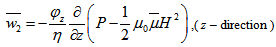
 are fluid permeabilities in the lower porous region in x and z directions respectively, and P is the fluid pressure in the porous region.(4)The continuity equation in the porous regions are given as follows:For upper porous region:
are fluid permeabilities in the lower porous region in x and z directions respectively, and P is the fluid pressure in the porous region.(4)The continuity equation in the porous regions are given as follows:For upper porous region: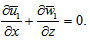
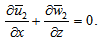
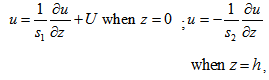
 are porosities in the x- direction for lower and upper porous regions respectively, one obtain
are porosities in the x- direction for lower and upper porous regions respectively, one obtain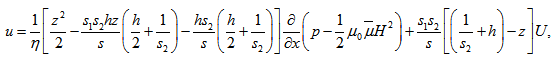
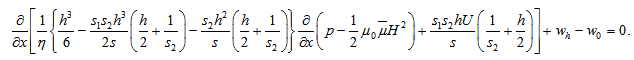
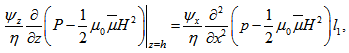
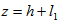 is non-porous.Substituting equations (15) and (16) in the continuity equation for lower porous region (18) and integrating with respect to z across the lower porous matrix (
is non-porous.Substituting equations (15) and (16) in the continuity equation for lower porous region (18) and integrating with respect to z across the lower porous matrix ( l2, 0 ), yields
l2, 0 ), yields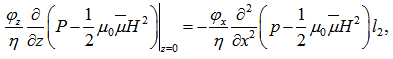
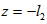 is non-porous.Considering the normal component of velocity across the film-porous interface are continuous, so that
is non-porous.Considering the normal component of velocity across the film-porous interface are continuous, so that 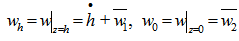 , using equations (14),(16),(21) and (22)-(23), one obtain
, using equations (14),(16),(21) and (22)-(23), one obtain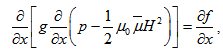
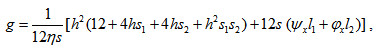
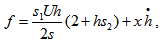 which is known as Reynolds’s type equation for the considered phenomenon.As mentioned earlier, here magnetic field is considered to be oblique to the lower plate and vanishing at the inlet and outlet of the bearing as
which is known as Reynolds’s type equation for the considered phenomenon.As mentioned earlier, here magnetic field is considered to be oblique to the lower plate and vanishing at the inlet and outlet of the bearing as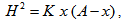
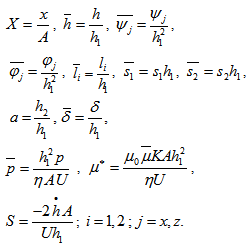 Then the dimensionless form of equations (1)-(5) and (24)-(25) becomes
Then the dimensionless form of equations (1)-(5) and (24)-(25) becomes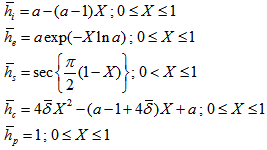 and
and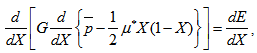
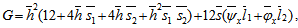
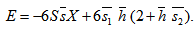
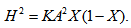
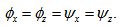 By following similar procedure as in Case 1, the following dimensionless form of Reynolds’s equation for isotropic permeable porous plate with respect to both upper and lower porous matrix is obtained. where
By following similar procedure as in Case 1, the following dimensionless form of Reynolds’s equation for isotropic permeable porous plate with respect to both upper and lower porous matrix is obtained. where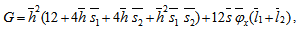
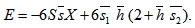
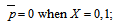 the dimensionless film pressure
the dimensionless film pressure 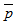 is obtained as follows:
is obtained as follows: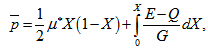 where
where 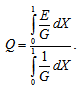 The load carrying capacity W is expressed in dimensionless form aswhere
The load carrying capacity W is expressed in dimensionless form aswhere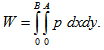 For anisotropic case G, E are given by equations (27)-(28), and for isotropic case G, E are given by equations (31)-(32).
For anisotropic case G, E are given by equations (27)-(28), and for isotropic case G, E are given by equations (31)-(32).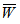 ) for various designed slider bearings ( that is, slider bearings having inclined pad stator, exponential pad stator, secant pad stator, convex pad stator, parallel pad stator ) are calculated for various sizes of upper and lower porous matrix using Simpson’s one third rule with step size 0.1, considering following values of the parameters :
) for various designed slider bearings ( that is, slider bearings having inclined pad stator, exponential pad stator, secant pad stator, convex pad stator, parallel pad stator ) are calculated for various sizes of upper and lower porous matrix using Simpson’s one third rule with step size 0.1, considering following values of the parameters :
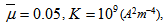
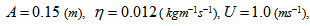
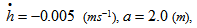
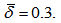 In the following cases, the notations used are
In the following cases, the notations used are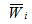 - Dimensionless load carrying capacity for slider bearing having inclined pad stator
- Dimensionless load carrying capacity for slider bearing having inclined pad stator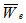 - Dimensionless load carrying capacity for slider bearing having exponential pad stator
- Dimensionless load carrying capacity for slider bearing having exponential pad stator 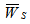 - Dimensionless load carrying capacity for slider bearing having secant pad stator
- Dimensionless load carrying capacity for slider bearing having secant pad stator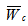 - Dimensionless load carrying capacity for slider bearing having convex pad stator
- Dimensionless load carrying capacity for slider bearing having convex pad stator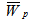 - Dimensionless load carrying capacity for slider bearing having parallel pad statorCase 1 For Anisotropic permeability
- Dimensionless load carrying capacity for slider bearing having parallel pad statorCase 1 For Anisotropic permeability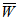 with slider bearing having parallel pad stator considering effects of porosity, slip velocity at both the ends, and squeeze velocity under an oblique magnetic field. The two cases of anisotropic permeability and isotropic permeability with respect to both upper and lower porous matrix are discussed for various sizes porous matrixes attached at both the plates. The following observations can be made from the results:(1) It is observed form tables 1-4 that maximum
with slider bearing having parallel pad stator considering effects of porosity, slip velocity at both the ends, and squeeze velocity under an oblique magnetic field. The two cases of anisotropic permeability and isotropic permeability with respect to both upper and lower porous matrix are discussed for various sizes porous matrixes attached at both the plates. The following observations can be made from the results:(1) It is observed form tables 1-4 that maximum 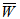 is obtained when
is obtained when 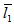 = 0 and
= 0 and 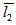 = 0. But with the insertation of porous layer at both the plates, maximum
= 0. But with the insertation of porous layer at both the plates, maximum 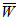 can be obtained when
can be obtained when 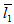 = 1 and
= 1 and 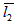 = 1. The almost same behaviour is obtained when
= 1. The almost same behaviour is obtained when 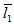 = 5 and
= 5 and 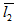 = 1; that is, when the porous layer attached to the upper plate (stator) is thick and porous layer attached to the lower plate (slider) is thin. But if we reverse the thickness of the porous plates; that is, when
= 1; that is, when the porous layer attached to the upper plate (stator) is thick and porous layer attached to the lower plate (slider) is thin. But if we reverse the thickness of the porous plates; that is, when 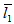 = 1 and
= 1 and 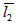 = 5 then the increase of
= 5 then the increase of 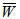 is substantially less. Moreover, the percentage increases in
is substantially less. Moreover, the percentage increases in 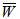 for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables. (2) It is observed form tables 5-8 that maximum
for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables. (2) It is observed form tables 5-8 that maximum 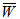 is obtained when
is obtained when 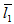 = 0 and
= 0 and 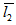 = 0 . But with the insertation of porous layer at both the plates, maximum
= 0 . But with the insertation of porous layer at both the plates, maximum 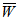 can be obtained when
can be obtained when 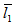 = 1 and
= 1 and 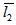 = 1. The almost same behaviour is obtained when
= 1. The almost same behaviour is obtained when 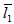 = 1 and
= 1 and 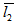 = 5; that is, when the porous layer attached to the lower plate (slider) is thick and porous layer attached to the upper plate (stator) is thin. But if we reverse the thickness of the porous plates; that is, when
= 5; that is, when the porous layer attached to the lower plate (slider) is thick and porous layer attached to the upper plate (stator) is thin. But if we reverse the thickness of the porous plates; that is, when 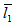 = 5 and
= 5 and 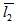 = 1 then the increase of
= 1 then the increase of 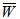 is substantially less. Moreover, the percentage increases in
is substantially less. Moreover, the percentage increases in 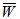 for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables.In summary, when the permeability of the upper porous layer is small as compared to lower porous layer, then
for various slider bearings with respect to slider bearing with parallel plate stator are as shown in tables.In summary, when the permeability of the upper porous layer is small as compared to lower porous layer, then 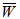 increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then
increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then 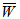 increases with the increase of thickness of lower porous layer.Thus, maximum
increases with the increase of thickness of lower porous layer.Thus, maximum 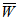 can be obtained when permeability decreases and thickness of the porous layer increases. It is observed form tables 9-11 that maximum
can be obtained when permeability decreases and thickness of the porous layer increases. It is observed form tables 9-11 that maximum 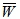 is obtained when
is obtained when 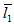 = 5 and
= 5 and 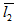 = 5 . Also,
= 5 . Also, 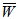 remains same whether
remains same whether 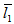 = 5 and
= 5 and 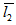 = 10 or
= 10 or 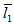 = 10 and
= 10 and 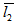 = 5. Similar type of behaviour for
= 5. Similar type of behaviour for 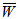 is obtained for tables 12-14. Moreover, for smaller values of permeabilities
is obtained for tables 12-14. Moreover, for smaller values of permeabilities 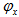 and
and 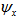 , better
, better 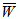 is obtained ( refer tables 9-11) as compared to larger values ( refer tables 12-14).The following table 15 indicates the comparison of
is obtained ( refer tables 9-11) as compared to larger values ( refer tables 12-14).The following table 15 indicates the comparison of 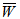 for various bearings.
for various bearings.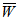 increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then
increases with the increase of thickness of upper porous layer. Similarly, when the permeability of the lower porous layer is small as compared to upper porous layer, then 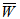 increases with the increase of thickness of lower porous layer.(3) For isotropic case more better
increases with the increase of thickness of lower porous layer.(3) For isotropic case more better 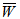 is obtained.(4) It should be noted that a constant magnetic field does not enhance
is obtained.(4) It should be noted that a constant magnetic field does not enhance 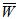 in this model since
in this model since 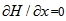 in equation (11).(5) It is observed form table 15 that the suggestive design of bearing is either inclined or convex pad stator surfaces and occasionally secant pad stator surface.
in equation (11).(5) It is observed form table 15 that the suggestive design of bearing is either inclined or convex pad stator surfaces and occasionally secant pad stator surface. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML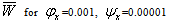

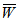 for
for 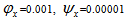
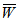 for
for 
 for
for 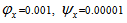
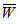 for
for 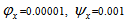
 for
for 
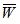 for
for 
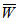 for
for 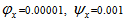
 for
for 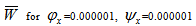
 for
for 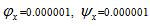
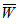 for
for 
 for
for 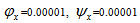
 for
for 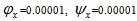
 for
for