1. Introduction

The concept of fixed point was initiated by H. Poincare in 1886. Metric space, in which the notion of distance appears was introduced by M.Frechet in 1906. Metric fixed point theory is an important branch of nonlinear analysis. It has applications in many branches of mathematics. Some of them are Control theory, Game theory, Nash equilibrium, Economics, Optimization theory, Differential equations and Boundary Value Problems etc. In 1922, S. Banach[4] proved a fixed point theorem for contraction mapping in complete metric space. Since then numerous generalizations of this theorem have been obtained by weakening its hypothesis while retaining the convergence property of successive iterates to the unique fixed point of the mappings. The concept of metric space has also been generalized in different directions during past three decades. Some important generalizations are, dislocated metric space, Quasi metric space, dislocated quasi metric space and generalized quasi metric spaces.

In 1994, S. Abramski and A. Jung[1] presented some facts about dislocated metric under the name of metric domains in the context of domain theory. In 2000, P. Hitzler and A. K. Seda[7] initiated the notion of dislocated metric space where, self distance for any point need not be equal to zero and generalized this celebrated Banach Contraction Principle in complete dislocated metric space. Dislocated metric space plays an important role in logic programming and electronics engineering.

In 2006, F. M. Zeyada et.al.[18] established various definitions and generalized the result of P. Hitzler and A. K. Seda in dislocated quasi metric space.

In 2008, C. T. Aage and J. N. Salunke[2] proved some results in dislocated and dislocated quasi-metric spaces. In 2010, A. Isufati[8] and in 2012, K. Jha and D. Panthi[10],

K. Jha et.al[11], R. Shrivastava et.al.[17] have also proved some results in these spaces.

The purpose of this paper is to establish a fixed point theorem for self mapping in dislocated quasi- metric space which generalizes and unifies some results.

We start with the following definitions.

Definition 1.[18] Let 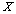be a non empty set and let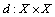 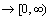be a function satisfying the following conditions:

M₁: d(x, x) = 0

M₂: 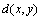= = 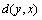0 implies

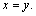M₃: d(x, y) = d(y, x)

M₄: d(x, y) 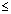d(x, z) + d(z, y) for all x, y, z 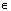X.

If d satisfies the condition M₁ - M₄ then d is called a metric on X. If d satisfies conditions M₂, M₃ and M₄ then it is called a dislocated metric(simply d- metric) and if d satisfies only M₂ and M₄ then d is called dislocated quasi- metric (or simply dq-metric) on X. The non empty set X together with dq- metric d, that is (X, d) is called a dislocated quasi metric space.

Definition 2: Let T be a continuous mapping of a non empty set X into itself. An element x in X is said to be fixed point of T if Tx = x.

Theorem (Banach’s Contraction Mapping) 1.[4] Let 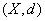be complete metric space and 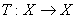be a map such that 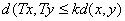for some 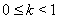and all 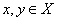. Then T has a unique fixed point in 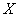. Moreover, for any 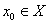the sequence of Picard iterates 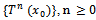, converges to the fixed point of T.

Definition 3.[18] A sequence 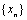in dislocated quasi-metric space (dq-metric space) (X , d) is called Cauchy sequence if for given 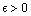, there corresponds 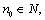such that for all m, n 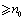, we have 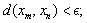or .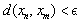

In above definition, if we replace 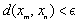or 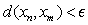by max {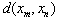, 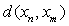} < 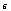, then {x_n} is called “bi” Cauchy.

Definition 4.[18] A sequence 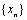in a dq-metric space 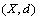is said to be dislocated quasi convergent (for short dq-convergent) to x if

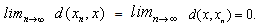In this case, x is called a dq-limit of 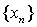and we write

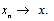Definition 5.[18] let (X, d₁) and (Y, d₂) be dq metric spaces and let T: X 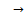Y be a function. Then T is continuous if for each sequence {x_n} which is d₁q-convergent to x₀ in X, the sequence {Tx_n} is d₂q-convergent to T(x₀) in Y.

Definition 6.[18] A dq-metric space (X, d) is called complete if every Cauchy sequence in it is a dq- convergent.

Definition 7.[18] Let (X, d) be a dq-metric space. A map 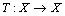is called contraction if there exists 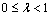such that d(Tx, Ty)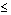 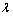d(x, y).

Lemma 1.[18] Every subsequence of dq-convergent sequence to a point 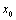is dq-convergent to.

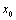Lemma 2.[18] Let (X, d) be a dq-metric space. If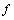: X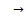 X is a contraction function, then 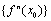is a Cauchy sequence for each

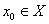Lemma 3.[18] dq-limits in a dq-metric space are unique.

Proof: Let x and y be dq limits of the sequence {x_n}.

Now using property M₄, we can write,

d(x,y) 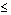d(x, x_n) + d(x_n, y)

Since the expression in right hand side tends to 0 as n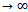, so d(x, y) = 0. Similarly we can show that d(y, x) = 0. Therefore x = y (using property M₂).

Here we present some theorems which ensure fixed points satisfying contractive type conditions and rational contractive conditions in metric space and dislocated quasi-metric space.

One of the extensions of Banach’s Contraction Mapping Theorem to become widely known is the following theorem due to E. Rakotch in 1962 in metric space.

Theorem 2.[16] Let (X, d) be a non empty complete metric space and suppose T: 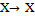satisfies

d(Tx, Ty) 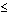α (d(x, y))d(x, y) for all x, y 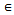X where, α:[0, 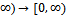is monotonically decreasing. Then, T has a unique fixed point z and for all x₀ 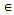X we have {Tⁿ(x₀)} 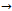z as .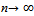

In 1968, R. Kannan obtained following theorem in metric space.

Theorem 3.[12] Let (X, d) be a non empty complete metric space. Let T : 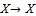such that there exists an 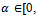1/2) for which

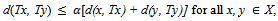then there exists a unique fixed point to which all the Picard iteration sequence converge to the fixed point.

In 1975, B. K. Dass and S. Gupta generalized Banach Contraction Mapping Theorem through rational expressions in metric space.

Theorem 4.[5] Let T be a mapping of X into itself such that

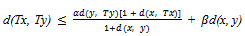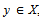
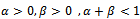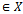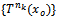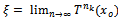for all x, and for some x₀ the sequence of iterates {Tⁿ(x₀)} has a subsequence with then 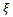is a unique fixed point of T.

In 1977, D. S. Jaggi established the following fixed point theorem using rational type contractive condition in complete metric space which generalizes the Banach Contraction Mapping Theorem.

Theorem 5.[9] Let T be a continuous self map defined on a complete metric space (X, d). Further let T satisfies the following contractive conditions

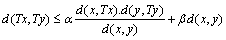for all 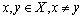for some 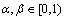with 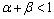, then T has a unique fixed point.

F. M. Zeyada et.al[18] established the following theorem in dislocated quasi-metric space in 2006.

Theorem 6.[18] Let (X, d) be a complete dq-metric space and let T: X 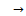X be a continuous contraction function. Then, T has a unique fixed point.

C. T. Aage and J. N. Salunke established the following theorem in dislocated quasi-metric space in 2008.

Theorem 7.[2] Let (X, d) be a complete dislocated quasi-metric space. Let 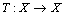be continuous mapping satisfying the condition

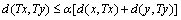for all 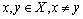,0≤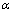< ½ , then T has a unique fixed point.

In 2010, A. Isufati established the following theorem in dislocated quasi- metric space.

Theorem 8.[8] Let (X, d) be a complete dislocated quasi-metric space. Let 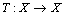be continuous mapping satisfying the condition,

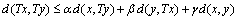Where 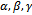are nonnegative, which may depend on both x and y such that sup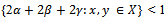. Then T has a unique fixed point.

R. Shrivastava, Z. K. Ansari and M. Sharma proved the following theorems in dislocated quasi metric space in 2012.

Theorem 9.[17] Let T be a continuous self map defined on a complete dq- metric space (X, d). Further, let T satisfies the contractive condition,

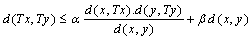for 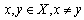for some 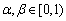with 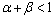, then T has a unique fixed point.

Theorem 10.[17] Let (X, d) be a complete dislocated quasi-metric space. Let 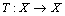be continuous mapping satisfying the condition,

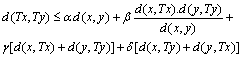for all 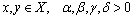, with 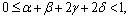then T has a unique fixed point.

K. Zoto, E. Hoxha and A. Isufati established the following theorem in dislocated quasi-metric space in 2012.

Theorem 11.[19] Let (X, d) be a complete dislocated quasi-metric space. Let 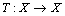be continuous mapping satisfying the condition,

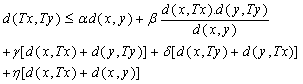for all 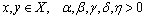, with 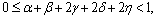then T has a unique fixed point.

Now, we establish the following theorem in dislocated quasi metric space as a main result. This theorem unifies and generalizes some well known results in the literature.

2. Main Result

Theorem 12. Let (X, d) be a complete dislocated quasi-metric space. Let 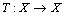be continuous mapping satisfying the condition,

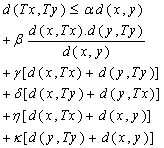(1)

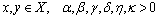for all , with 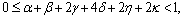then T has a unique fixed point.

Proof: Let us define a sequence as follows: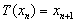

, for n = 0, 1, 2, ....

Also, let 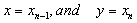, Then, by relation (1), we have,

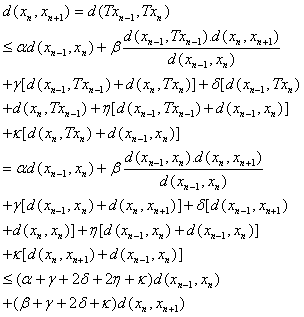hence,

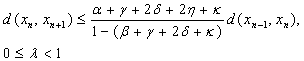Thus, we have

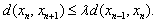where,

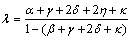, with

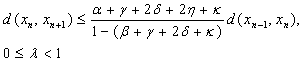Similarly, we get

.

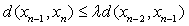Hence, we have

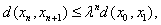Now, for any m, n, m > n, using triangle inequality we get,

d(x_n , x_m ) ≤ d(x_n , x_n+1 ) + d(x_n+1 , x_n+2 )+ ……+d(x_m-1 , x_m )

= ++ …+

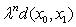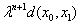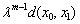
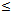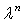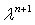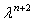(+ + + …) d(x₀ , x₁) =

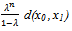For any 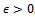, choose 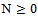such that, ,

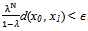Then for any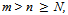

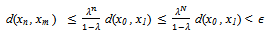Similarly, we can show that

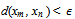Hence, 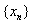is a Cauchy sequence in complete dislocated quasi- metric space (X, d). So, there exists a point 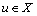and {x_n} dislocated quasi converge to the point u.

Since T is continuous, so we have,

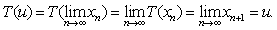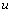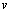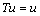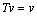Uniqueness: If possible, let and are two fixed points of T so that, by definition, and . Let 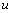be fixed. Then, the relation (1) gives

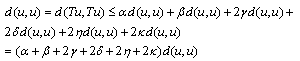which implies that 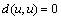, since .

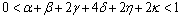Thus, we have .

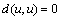Similarly, we get 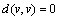, for 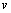fixed.

Again, from relation (1), we have

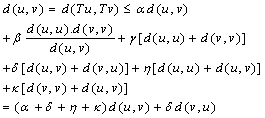(2)

Similarly, we get

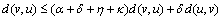(3)

Hence, from relations (2) and (3) we obtain

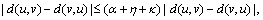which is a contradiction.

So, we have

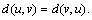Again by relation (1) with substitutions, we obtain

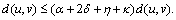which implies that, .

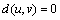Hence, we have .

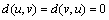Therefore, we have .

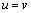This completes the proof of theorem.

Remarks: In Theorem 12

(1) If we put 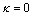, we get the Theorem 3.1 of K. Zoto, E. Hoxha and A. Isufati[19].

(2) If we put 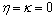, we obtain the Theorem 3.5 of R. Shrivastav, Z. K. Ansari and M. Sharma[17] .

(3) If we put 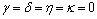, we obtain Theorem 3.3 of Shrivastav[17].

(4) If we put 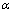=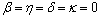, we obtain the Theorem 3.3 of C. T. Aage and J. N. Salunke[2].

(5) If we put 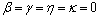, we get Theorem 3.2 of A. Isufati with their two coefficients equal[8].

(6) If we put 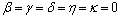, we get the Theorem 2.1 of F. M. Zeyada et.al.[18].

Thus, our result extends the results of[19],[17],[2],[8],[18] and other similar results.

ACKNOWLEDGEMENTS

Authors are thankful to the referees for their valuable suggestions to improve the manuscript. Also, the first author is thankful to University Grants Commission (UGC), Nepal for providing research fellowship at Kathmandu University, Nepal.