-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(3): 143-152
doi:10.5923/j.ajms.20130303.07
Relations Connecting Eighth Order Mock Theta Functions
Roselin Antony
Department of Mathematics, College of Natural and Computational Sciences, Mekelle University, Mekelle, P.O. Box 231, Ethiopia
Correspondence to: Roselin Antony, Department of Mathematics, College of Natural and Computational Sciences, Mekelle University, Mekelle, P.O. Box 231, Ethiopia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
During the last years of his life, Ramanujan defined 17 functions F(q), where | q | < 1, and he named them as mock theta functions. The first detailed description of mock theta functions was given by Watson. In this paper, we obtain relations connecting mock theta functions, partial mock theta functions of order 8 and infinite products analogous to the identities of Ramanujan.
Keywords: Mock Theta Functions, Partial Mock Theta Functions, Infinite Products
Cite this paper: Roselin Antony, Relations Connecting Eighth Order Mock Theta Functions, American Journal of Mathematics and Statistics, Vol. 3 No. 3, 2013, pp. 143-152. doi: 10.5923/j.ajms.20130303.07.
1. Introduction
- Ramanujan gave a list of seventeen mock theta functions and labeled them as third, fifth and seventh orders without giving any reason for his classification [1, 2]. Ramanujan’s general definition of a mock theta function is a function of
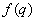 defined by a q-series convergent when | q | < 1 which satisfies the following two conditions,(a) For every root
defined by a q-series convergent when | q | < 1 which satisfies the following two conditions,(a) For every root 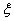 of unity, there exist a
of unity, there exist a 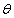 -function
-function 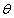 (q) such that difference between
(q) such that difference between 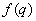 and
and 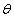 (q) is bounded as q
(q) is bounded as q 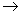
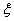 , radially.(b) There is no single theta function which works for all
, radially.(b) There is no single theta function which works for all 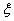 , i.e. for every
, i.e. for every 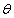 -function
-function 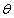 (q) there is some root of unity
(q) there is some root of unity 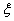 for which
for which 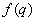 minus the theta function
minus the theta function 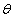 (q) is unbounded as q
(q) is unbounded as q 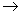
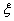 radially. A study of these sums and expansions has been made by Watson[3], Agarwal[4] and Andrews[5]. Later on, Andrews and Hickerson[6], Choi[7] and Gordon and Mc Intosh[8] studied certain q-series in the Lost Notebook and named them as sixth, eighth and tenth order mock theta functions. Although Gordon and Mc Intosh[8] have given definitions of order of mock theta functions, and later Bringmann and Ono[9, 10] have given clarification for the order of the mock theta functions.Also, relations connecting mock theta functions and partial mock theta functions are given by Srivastava[11] and Denis et al.[12]. Bhaskar Srivastava[13] provided relations connecting mock theta functions and partial mock theta functions of order 3, 5, 6 and 10 and relations connecting mock theta functions, partial mock theta functions of order 2, 3 and 6 and Ramanujan’s function μ(q). Recently, Roselin Antony and Atakalti Araya[14] obtained relations connecting mock theta functions of order 2 and infinite products analogous to the identities of Ramanujan. Also, Roselin Antony and Hailemariam Fiseha[15] obtained relations connecting mock theta functions of order 10 and infinite products analogous to the identities of Ramanujan. Also, Roselin Antony[16] obtained relations connecting mock theta functions of order 6 and infinite products analogous to the identities of Ramanujan
radially. A study of these sums and expansions has been made by Watson[3], Agarwal[4] and Andrews[5]. Later on, Andrews and Hickerson[6], Choi[7] and Gordon and Mc Intosh[8] studied certain q-series in the Lost Notebook and named them as sixth, eighth and tenth order mock theta functions. Although Gordon and Mc Intosh[8] have given definitions of order of mock theta functions, and later Bringmann and Ono[9, 10] have given clarification for the order of the mock theta functions.Also, relations connecting mock theta functions and partial mock theta functions are given by Srivastava[11] and Denis et al.[12]. Bhaskar Srivastava[13] provided relations connecting mock theta functions and partial mock theta functions of order 3, 5, 6 and 10 and relations connecting mock theta functions, partial mock theta functions of order 2, 3 and 6 and Ramanujan’s function μ(q). Recently, Roselin Antony and Atakalti Araya[14] obtained relations connecting mock theta functions of order 2 and infinite products analogous to the identities of Ramanujan. Also, Roselin Antony and Hailemariam Fiseha[15] obtained relations connecting mock theta functions of order 10 and infinite products analogous to the identities of Ramanujan. Also, Roselin Antony[16] obtained relations connecting mock theta functions of order 6 and infinite products analogous to the identities of Ramanujan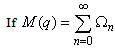 | (1.1) |
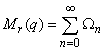 | (1.2) |
2. Methodology
- We shall make use of mock theta functions of order 8, their partial sums and infinite products in the known identity of Srivastava[11] to obtain new relations connecting mock theta functions of order 8. Mock theta functions of order 8:Gordon and McIntosh[8] found the following eight mock theta functions of order 8;
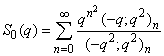 | (1.3) |
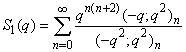 | (1.4) |
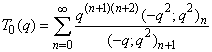 | (1.5) |
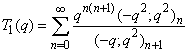 | (1.6) |
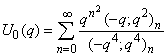 | (1.7) |
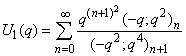 | (1.8) |
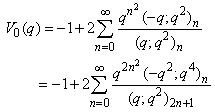 | (1.9) |
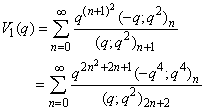 | (1.10) |
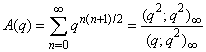 | (1.11) |
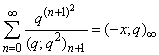 | (1.12) |
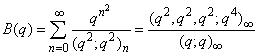 | (1.13) |
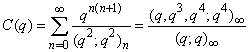 | (1.14) |
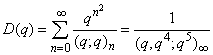 | (1.15) |
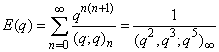 | (1.16) |
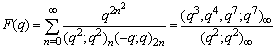 | (1.17) |
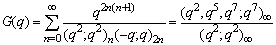 | (1.18) |
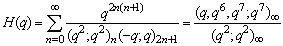 | (1.19) |
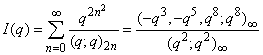 | (1.20) |
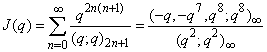 | (1.21) |
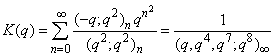 | (1.22) |
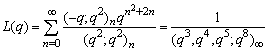 | (1.23) |
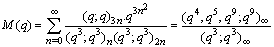 | (1.24) |
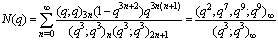 | (1.25) |
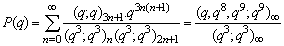 | (1.26) |
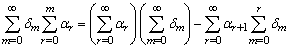 | (1.27) |
3. Main Results and Discussion
- We shall establish relations connecting mock theta functions, partial mock theta functions of order 8 and infinite products analogous to the identities of Ramanujan.A) Taking
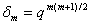 in (1.27) and by (1.11), we get
in (1.27) and by (1.11), we get 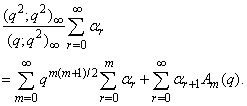 | (2.1) |
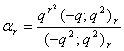 in (2.1) and making use of (1.3), we get
in (2.1) and making use of (1.3), we get 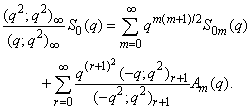 | (2.2) |
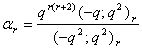 in (2.1) and making use of (1.4), we get
in (2.1) and making use of (1.4), we get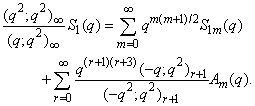 | (2.3) |
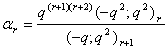 in (2.1) and making use of (1.5), we get
in (2.1) and making use of (1.5), we get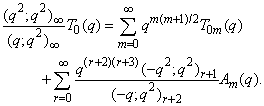 | (2.4) |
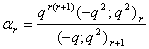 in (2.1) and making use of (1.6), we get
in (2.1) and making use of (1.6), we get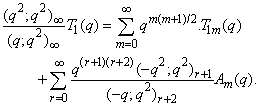 | (2.5) |
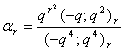 in (2.1) and making use of (1.7), we get
in (2.1) and making use of (1.7), we get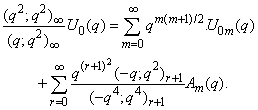 | (2.6) |
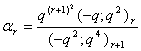 in (2.1) and making use of (1.8), we get
in (2.1) and making use of (1.8), we get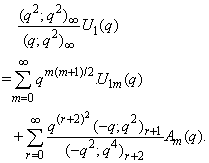 | (2.7) |
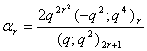 in (2.1) and making use of (1.9), we get
in (2.1) and making use of (1.9), we get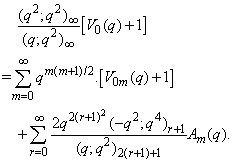 | (2.8) |
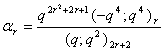 in (2.1) and making use of (1.10), we get
in (2.1) and making use of (1.10), we get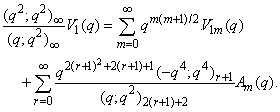 | (2.9) |
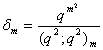 in (1.27) and by (1.13), we get
in (1.27) and by (1.13), we get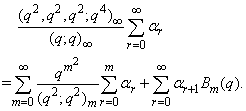 | (2.10) |
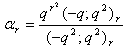 in (2.10) and making use of (1.3), we get
in (2.10) and making use of (1.3), we get 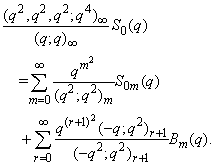 | (2.11) |
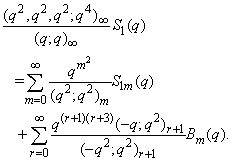 | (2.12) |
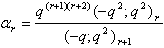 in (2.10) and making use of (1.5), we get
in (2.10) and making use of (1.5), we get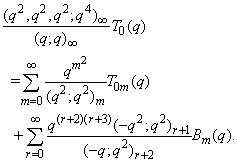 | (2.13) |
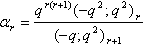 in (2.10) and making use of (1.6), we get
in (2.10) and making use of (1.6), we get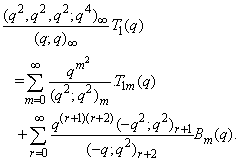 | (2.14) |
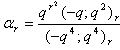 in (2.10) and making use of (1.7), we get
in (2.10) and making use of (1.7), we get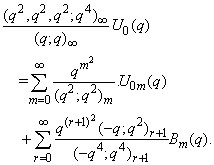 | (2.15) |
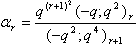 in (2.10) and making use of (1.8), we get
in (2.10) and making use of (1.8), we get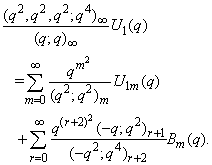 | (2.16) |
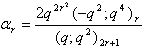 in (2.10) and making use of (1.9), we get
in (2.10) and making use of (1.9), we get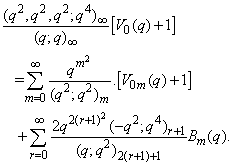 | (2.17) |
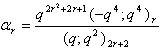 in (2.10) and making use of (1.10), we get
in (2.10) and making use of (1.10), we get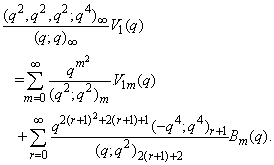 | (2.18) |
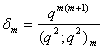 , we can establish relations connecting mock theta functions of order 6 and the infinite product C(q).C) Taking
, we can establish relations connecting mock theta functions of order 6 and the infinite product C(q).C) Taking 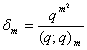 in (1.27) and by (1.15), we get
in (1.27) and by (1.15), we get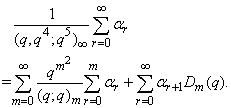 | (2.19) |
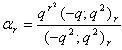 in (2.19) and making use of (1.3), we get
in (2.19) and making use of (1.3), we get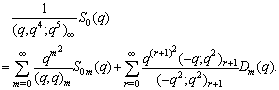 | (2.20) |
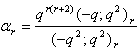 in (2.19) and making use of (1.4), we get
in (2.19) and making use of (1.4), we get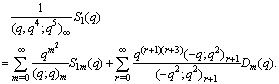 | (2.21) |
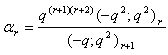 in (2.19) and making use of (1.5), we get
in (2.19) and making use of (1.5), we get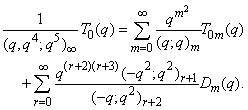 | (2.22) |
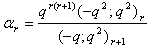 in (2.19) and making use of (1.6), we get
in (2.19) and making use of (1.6), we get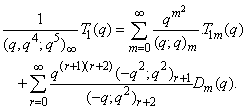 | (2.23) |
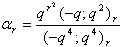 in (2.19) and making use of (1.7), we get
in (2.19) and making use of (1.7), we get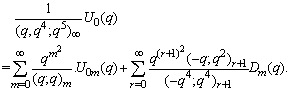 | (2.24) |
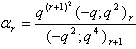 in (2.19) and making use of (1.8), we get
in (2.19) and making use of (1.8), we get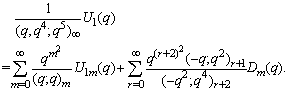 | (2.25) |
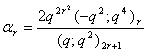 in (2.19) and making use of (1.9), we get
in (2.19) and making use of (1.9), we get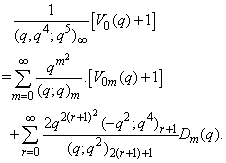 | (2.26) |
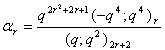 in (2.19)and making use of (1.10), we get
in (2.19)and making use of (1.10), we get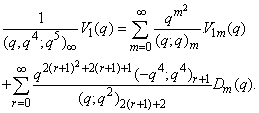 | (2.27) |
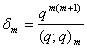 , relations can be developed connecting mock theta functions and the infinite product E(q).D) Taking
, relations can be developed connecting mock theta functions and the infinite product E(q).D) Taking 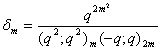 in (1.27) and by (1.17), we get
in (1.27) and by (1.17), we get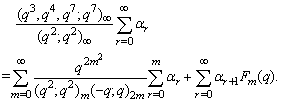 | (2.28) |
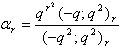 in (2.28) and by (1.3), we get
in (2.28) and by (1.3), we get 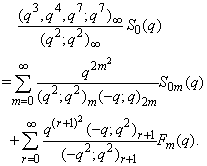 | (2.29) |
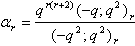 in (2.28) and by (1.4), we get
in (2.28) and by (1.4), we get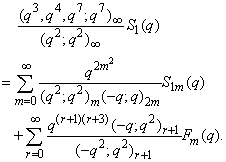 | (2.30) |
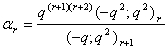 in (2.28)and by (1.5), we get
in (2.28)and by (1.5), we get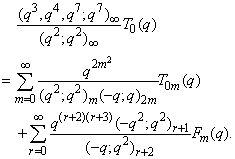 | (2.31) |
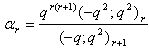 in (2.28) and by (1.6), we get
in (2.28) and by (1.6), we get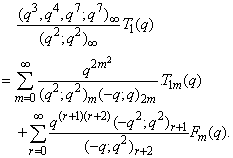 | (2.32) |
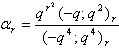 in (2.28) and by (1.7), we get
in (2.28) and by (1.7), we get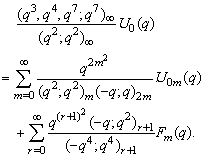 | (2.33) |
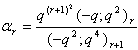 in (2.28) and by (1.8), we get
in (2.28) and by (1.8), we get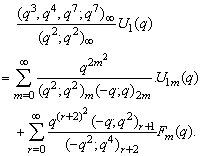 | (2.34) |
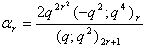 in (2.28) and by (1.9), we get
in (2.28) and by (1.9), we get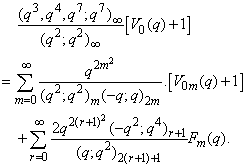 | (2.35) |
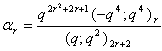 in (2.28) and by (1.10), we get
in (2.28) and by (1.10), we get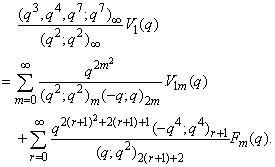 | (2.36) |
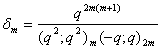 and
and 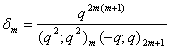 , relations connecting mock theta functions of order six and the infinite products G(q) and H(q) can be obtained.E) Taking
, relations connecting mock theta functions of order six and the infinite products G(q) and H(q) can be obtained.E) Taking 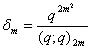 in (1.27) and by (1.20), we get
in (1.27) and by (1.20), we get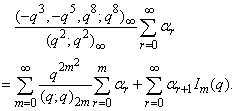 | (2.37) |
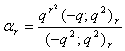 in (2.37) and by (1.3), we get
in (2.37) and by (1.3), we get 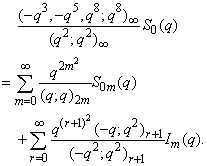 | (2.38) |
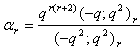 in (2.37) and by (1.4), we get
in (2.37) and by (1.4), we get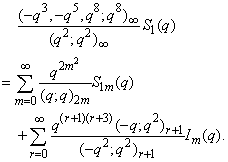 | (2.39) |
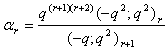 in (2.37) and by (1.5), we get
in (2.37) and by (1.5), we get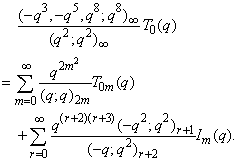 | (2.40) |
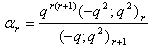 in (2.37) and by (1.6), we get
in (2.37) and by (1.6), we get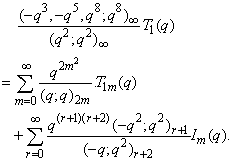 | (2.41) |
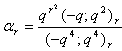 in (2.37) and by (1.7), we get
in (2.37) and by (1.7), we get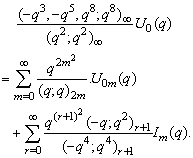 | (2.42) |
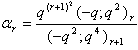 in (2.37) and by (1.8), we get
in (2.37) and by (1.8), we get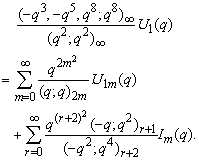 | (2.43) |
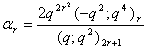 in (2.37) and by (1.9), we get
in (2.37) and by (1.9), we get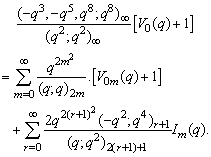 | (2.44) |
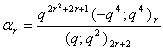 in (2.37) and by (1.10), we get
in (2.37) and by (1.10), we get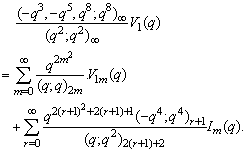 | (2.45) |
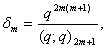
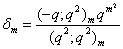 and
and 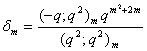 , relations connecting mock theta functions of order six and the infinite products J(q), K(q) and L(q) can be obtained.F) Taking
, relations connecting mock theta functions of order six and the infinite products J(q), K(q) and L(q) can be obtained.F) Taking 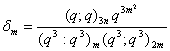 in (1.27) and by (1.24), we get
in (1.27) and by (1.24), we get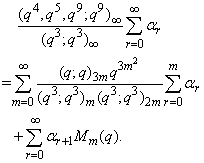 | (2.46) |
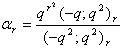 in (2.46) and by (1.3), we get
in (2.46) and by (1.3), we get 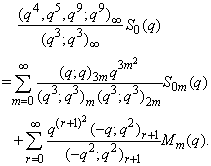 | (2.47) |
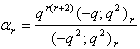 in (2.46) and by (1.4), we get
in (2.46) and by (1.4), we get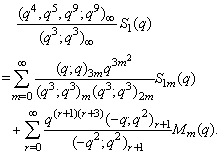 | (2.48) |
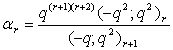 in (2.46) and by (1.5), we get
in (2.46) and by (1.5), we get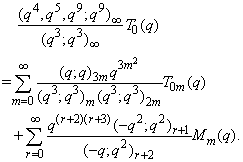 | (2.49) |
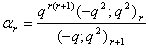 in (2.46) and by (1.6), we get
in (2.46) and by (1.6), we get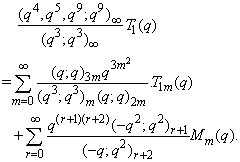 | (2.50) |
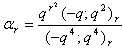 in (2.46) and by (1.7), we get
in (2.46) and by (1.7), we get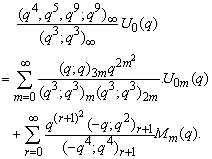 | (2.51) |
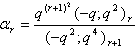 in (2.46) and by (1.8), we get
in (2.46) and by (1.8), we get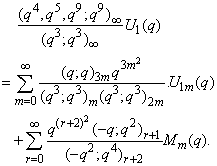 | (2.52) |
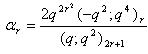 in (2.46) and by (1.9), we get
in (2.46) and by (1.9), we get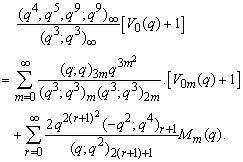 | (2.53) |
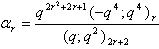 in (2.46) and by (1.10), we get
in (2.46) and by (1.10), we get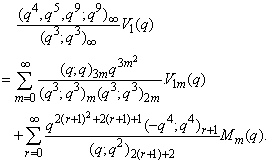 | (2.54) |
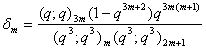 and
and 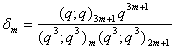 , relations connecting mock theta functions of order six and the infinite products N(q) and P(q) can be obtained.Similar works have been done on mock theta functions of order 8 by various mathematicians. Ahmad Ali[30] obtained relations connecting mock theta functions of order 8 and various mock theta functions of other orders. Maheshwar Pathak and Pankaj Srivastava[31] established relations connecting connecting partial mock theta functions and mock theta functions of order two, six, eight and ten.
, relations connecting mock theta functions of order six and the infinite products N(q) and P(q) can be obtained.Similar works have been done on mock theta functions of order 8 by various mathematicians. Ahmad Ali[30] obtained relations connecting mock theta functions of order 8 and various mock theta functions of other orders. Maheshwar Pathak and Pankaj Srivastava[31] established relations connecting connecting partial mock theta functions and mock theta functions of order two, six, eight and ten.4. Conclusions
- In the similar way, many relations can be obtained using mock theta functions of different orders and infinite products analogous to Ramanujan’s identities.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML