-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(3): 124-129
doi:10.5923/j.ajms.20130303.04
Polygon Semi Designs
1Department of Mathematics, University of the Punjab Lahore
2Department of Mathematics, (University of Management and Technology Lahore, Pakistan)
Correspondence to: Khalil Ahmad, Department of Mathematics, (University of Management and Technology Lahore, Pakistan).
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper a family of semi design 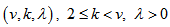 , named as polygon semi design is introduced. These designs are generated from polygon graphs, Polygon graphs are bicubic simple graphs. Polygon graphs possess Hamiltonian cycles and have girth 6.
, named as polygon semi design is introduced. These designs are generated from polygon graphs, Polygon graphs are bicubic simple graphs. Polygon graphs possess Hamiltonian cycles and have girth 6. 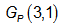 Polygon graph is isomorphic to a famous Pappus graph. Polygon semi designs are symmetric. Several results are proved on these designs. Upper and lower bounds for stopping sets are determined. Incidence matrix of polygon semi design can be used as parity check matrix of a famous low density parity check codes.
Polygon graph is isomorphic to a famous Pappus graph. Polygon semi designs are symmetric. Several results are proved on these designs. Upper and lower bounds for stopping sets are determined. Incidence matrix of polygon semi design can be used as parity check matrix of a famous low density parity check codes.
Keywords: Polygon Graph, Girth, Hamiltonian Cycle, Bipartite Graph, Combinatorial Design, Stopping Set
Cite this paper: Shoaibu Din, Khalil Ahmad, Polygon Semi Designs, American Journal of Mathematics and Statistics, Vol. 3 No. 3, 2013, pp. 124-129. doi: 10.5923/j.ajms.20130303.04.
Article Outline
1. Preliminaries and Introduction
- A graph G is a triple consisting of a vertex set V= V(G), an edge set E=E(G) and a map that associates to each edge two vertices (not necessarily distinct) called its end points. A loop is an edge whose end points are equal. Multiple edges are edges having same end points. A simple graph is one having no loops or multiple edges. To any graph, we can associate the adjacency matrix A which is an nn matrix (n=IvI) with rows and columns indexed by the elements of vertex set and the (x,y)-th entry is the number of edges connecting x and y.Cubic graphs also known as trivalent graphs are intensively studied in graph theory. The bipartite cubic graphs widely known as bicubic graphs took special interest. In 1884, P.G. Tait conjectured that every 3-connected planar cubic graph has a Hamiltonian cycle. Tutte, in 1946, provided a counter-example to the conjecture by constructing a 46-vertex graph.In 1971, Tutte [1] conjectured that all 3-connected bicubic graphs are Hamiltonian. J.D. Horton [2] in 1976 provided a counter-example to the conjecture by constructing a 96-vertex graph.Polygon graphs are structured by connecting odd number of copies of polygons of same size in a delicate manner. These graphs are defined only for polygon with even number of sides and denoted by Gp(m,p), where 2m is the number of sides and 2p +1 is the number of copies of polygon P. These graphs are bicubic with some interesting properties. Principle of mathematical induction is used to prove the existence of Hamiltonian cycles in these graphs. It is shown that these graphs have girth 6. It is a simple fact that cubic Hamiltonian graphs have at least two Hamiltonian cycles.An incidence structure is defined on polygon simple graph Gp(m,p) through a matrix, where rows of are taken as points and columns as blocks.Let
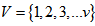 . A collection
. A collection 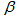 of distinct subsets of
of distinct subsets of 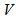 is called Polygon Semi Design
is called Polygon Semi Design 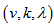 if
if 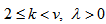 anda) Each set in
anda) Each set in 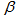 contains exactly
contains exactly 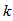 elements.b) Each two element subset of
elements.b) Each two element subset of 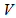 is contained in at most
is contained in at most 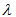 of the sets in
of the sets in 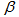 .The sets of
.The sets of 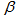 are called blocks and the number of blocks in
are called blocks and the number of blocks in 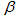 is denoted by
is denoted by 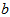 ; the set
; the set 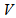 is called the base set.Balanced Incomplete Block Designs are different from Polygon Semi Designs as in BIBD, Each two element subset of
is called the base set.Balanced Incomplete Block Designs are different from Polygon Semi Designs as in BIBD, Each two element subset of 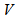 is contained in exactly
is contained in exactly 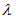 of the sets in
of the sets in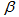 . Whereas in PSD, Each two element subset of
. Whereas in PSD, Each two element subset of 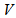 is contained in at most
is contained in at most 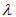 of the sets in
of the sets in 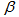 [8].Example 1.1 Let,
[8].Example 1.1 Let, 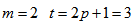 . Then
. Then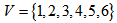
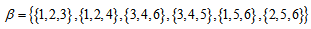 is a PSD
is a PSD 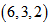 induced upon
induced upon 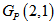 It is proved that polygon semi designs are symmetric. We also studied stopping sets in PSD,s which essentially require combinatorial mathematics[6].Incidence matrix of polygon semi design can be used as parity check matrix of a famous low density parity check codes. The size of the smallest stopping set in LDPC codes helps in analyzing their performance under iterative decoding, just as minimum distance helps in analyzing the performance under maximum likelihood decoding[7].The structure of the paper is as follows. In section 2, we introduce the definitions and notation used in the later sections; it also includes some results on polygon simple graphs. In section 3 polygon semi designs are defined on polygon simple graphs, a lower bound for the size of the smallest stopping set in a PSD is proposed.
It is proved that polygon semi designs are symmetric. We also studied stopping sets in PSD,s which essentially require combinatorial mathematics[6].Incidence matrix of polygon semi design can be used as parity check matrix of a famous low density parity check codes. The size of the smallest stopping set in LDPC codes helps in analyzing their performance under iterative decoding, just as minimum distance helps in analyzing the performance under maximum likelihood decoding[7].The structure of the paper is as follows. In section 2, we introduce the definitions and notation used in the later sections; it also includes some results on polygon simple graphs. In section 3 polygon semi designs are defined on polygon simple graphs, a lower bound for the size of the smallest stopping set in a PSD is proposed.2. Polygon Graph
- Let P be a polygon with
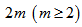 sides. Place 2p+1 copies of P denoted by
sides. Place 2p+1 copies of P denoted by 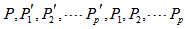 in parallel such that P is in the middle, p copies on the right side of P say
in parallel such that P is in the middle, p copies on the right side of P say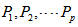 and p copies on the left side of P say
and p copies on the left side of P say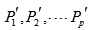 as follows.
as follows. 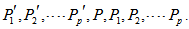 Vertices of P,
Vertices of P, 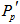 and
and 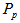 are denoted by
are denoted by 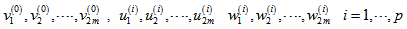 respectively. Simple connected graph
respectively. Simple connected graph  is constructed by drawing edges, such that an even vertex is connected with odd vertex and an odd vertex with even one in the following manner.i. Edges between vertices of different polygons.a) For j
is constructed by drawing edges, such that an even vertex is connected with odd vertex and an odd vertex with even one in the following manner.i. Edges between vertices of different polygons.a) For j with m vertices of 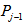 and m vertices of
and m vertices of 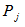 with m vertices of
with m vertices of 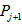 . Similarly connect m vertices of
. Similarly connect m vertices of 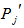 with m vertices of
with m vertices of 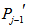 and m vertices of
and m vertices of 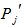 with m vertices of
with m vertices of 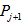 .
.
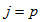 m vertices of
m vertices of 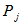 are already joined with m vertices of
are already joined with m vertices of 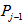 where the remaining m vertices of
where the remaining m vertices of 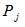 are joined with remaining m vertices of
are joined with remaining m vertices of 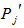 .where
.where 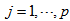 ii. Edges between vertices within a polygonOnly sides of polygon represent edges in
ii. Edges between vertices within a polygonOnly sides of polygon represent edges in 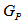 This simple graph is denoted by
This simple graph is denoted by 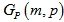 is named as polygon graph.
is named as polygon graph.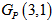 is isomorphic to a famous bicubic symmetric distance-regular Pappus graph with 18 vertices. It has following representations.
is isomorphic to a famous bicubic symmetric distance-regular Pappus graph with 18 vertices. It has following representations.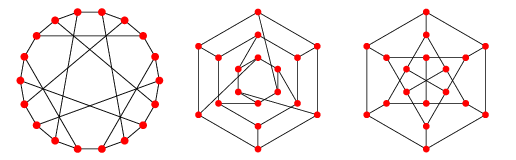 | Figure 1. Polygon graph Gp (3 , 1) |
 be a polygon graph. then.i) |
be a polygon graph. then.i) | | = 2m (2p+1) |
| = 2m (2p+1) | | = 3m (2p+1)ii)
| = 3m (2p+1)ii) 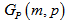 is a cubic graphiii)
is a cubic graphiii) 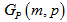 is a bipartite graph.Proof:i) Since each polygon has 2m number of vertices and there are (2p+1) copies of polygons in
is a bipartite graph.Proof:i) Since each polygon has 2m number of vertices and there are (2p+1) copies of polygons in 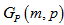 . |
. |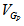 | =2m (2p+1)
| =2m (2p+1)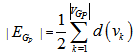 where
where 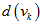 is the degree of
is the degree of 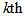 vertex.
vertex.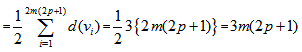 ii) By definition of
ii) By definition of 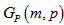 it is clear that each vertex of a polygon is connected with two vertices of the same polygon and with one vertex of a polygon either on its right or on its left. Hence degree of each vertex becomes three. So
it is clear that each vertex of a polygon is connected with two vertices of the same polygon and with one vertex of a polygon either on its right or on its left. Hence degree of each vertex becomes three. So 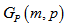 is a regular simple graph of degree three i.e.
is a regular simple graph of degree three i.e. 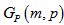 is a cubic graph.iii) There exist a vertex labeling such that each even vertex is connected with three odd vertices and each odd vertex is connected with three even vertices, therefore vertices of
is a cubic graph.iii) There exist a vertex labeling such that each even vertex is connected with three odd vertices and each odd vertex is connected with three even vertices, therefore vertices of 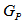 can be colored using only two colors. As every two colorable graph is bipartite. Hence
can be colored using only two colors. As every two colorable graph is bipartite. Hence 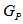 is bipartite graph with equal number of vertices in each part. Theorem 2.2:
is bipartite graph with equal number of vertices in each part. Theorem 2.2: 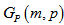 is a Hamiltonian graph i.e. it contains a Hamiltonian cycle!.Proof: Let m = 2, we use mathematical induction on p, to prove the result. For p= 1
is a Hamiltonian graph i.e. it contains a Hamiltonian cycle!.Proof: Let m = 2, we use mathematical induction on p, to prove the result. For p= 1 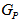 (2,1) contains Hamiltonian path.1 – 2 – 3 – 4 – 11 – 12 – 9 – 10 – 7 – 8 – 5 – 6 as shown in fig 2.
(2,1) contains Hamiltonian path.1 – 2 – 3 – 4 – 11 – 12 – 9 – 10 – 7 – 8 – 5 – 6 as shown in fig 2.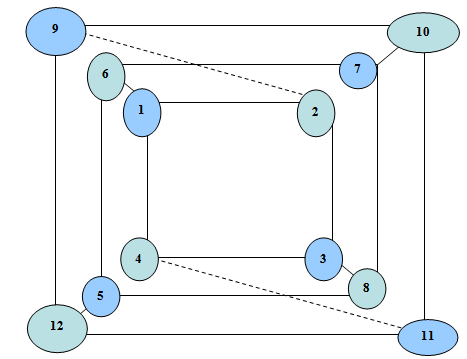 | Figure 2. Polygon graph Gp(2,1) |
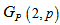 contain Hamiltonian cycle for
contain Hamiltonian cycle for  i.e.
i.e. 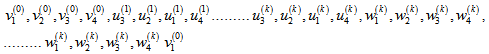 Now we prove that
Now we prove that  contains Hamiltonian cycle for
contains Hamiltonian cycle for 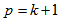 Replace edges between
Replace edges between 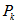 and
and 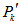 by drawing edges between
by drawing edges between 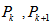 and
and 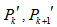 . Now we have two vertices of
. Now we have two vertices of 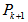 and two vertices of
and two vertices of 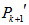 each of degree two; now connect these vertices to make the following path.
each of degree two; now connect these vertices to make the following path. 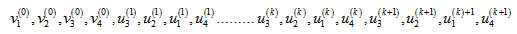
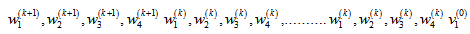 is a Hamiltonian path. Similarly it could be proved that for arbitrary
is a Hamiltonian path. Similarly it could be proved that for arbitrary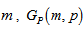 has Hamiltonian cycle.
has Hamiltonian cycle.  Theorem 2.3: Let
Theorem 2.3: Let 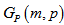 be a simple graph, where
be a simple graph, where 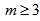 , Then the girth of
, Then the girth of 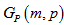 is 6 i.e.
is 6 i.e. 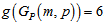 .Proof: Since
.Proof: Since 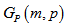 is a bipartite graph. The girth must be an even number. We consider two cases depending on the types of cycles in
is a bipartite graph. The girth must be an even number. We consider two cases depending on the types of cycles in 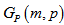 Case 1: Cycles containing the vertices of one polygon.Since there are 2m (
Case 1: Cycles containing the vertices of one polygon.Since there are 2m (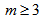 ) vertices in each polygon,
) vertices in each polygon, 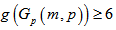 Case 1: Cycles involving the vertices of more than one polygon.In this case the shortest cycle must involve at least two vertices from two adjacent polygons i.e. two edges from each polygon. Moreover one edge is required to switch from one polygon to the other and another edge to come back. Thus
Case 1: Cycles involving the vertices of more than one polygon.In this case the shortest cycle must involve at least two vertices from two adjacent polygons i.e. two edges from each polygon. Moreover one edge is required to switch from one polygon to the other and another edge to come back. Thus 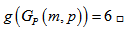
3. Polygon Semi Design
3.1. Definitions
- Let
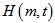 where
where 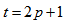 be a matrix whose columns represent odd labeled vertices and rows represent even labeled vertices of a polygon simple graph
be a matrix whose columns represent odd labeled vertices and rows represent even labeled vertices of a polygon simple graph 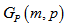 or vice versa, such that
or vice versa, such that  Example 3.1. Refer to the polygon graph
Example 3.1. Refer to the polygon graph 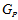 (2 , 1) in figure 2.
(2 , 1) in figure 2.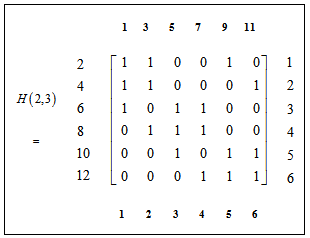 Theorem 3.1: Let PSD
Theorem 3.1: Let PSD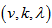 be a Polygon Semi Design. Then
be a Polygon Semi Design. Then 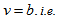 PSD is symmetric.Proof: From theorem 5.1 total number of vertices equals
PSD is symmetric.Proof: From theorem 5.1 total number of vertices equals 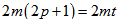 , where
, where 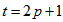 which is an even number. Hence if we label all vertices from
which is an even number. Hence if we label all vertices from 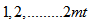 , since even label vertices are taken as points i.e.
, since even label vertices are taken as points i.e. 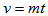 and odd vertices as blocks
and odd vertices as blocks 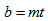 , Hence
, Hence 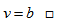 Theorem 3.2 If PSD
Theorem 3.2 If PSD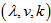 is a polygon semi design then each element of the base set occurs in
is a polygon semi design then each element of the base set occurs in 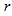 blocks, where
blocks, where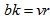 and
and 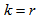 Proof: To prove the claim we count in two ways the cardinality of the set.
Proof: To prove the claim we count in two ways the cardinality of the set.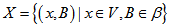 for each
for each 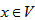 the block can be chosen in
the block can be chosen in 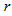 different ways, hence by product rule
different ways, hence by product rule 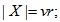 on the other hand, for each of the
on the other hand, for each of the 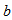 blocks can be chosen in different ways, again by product rule
blocks can be chosen in different ways, again by product rule 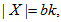 So
So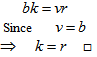
3.2. Incidence Matrix
- If PSD is a
 polygon semi design then the binary
polygon semi design then the binary 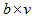 matrix
matrix 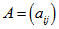 where
where 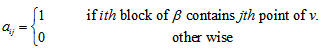 Is called incidence matrix of the PSD.Of course such a matrix is by no means unique, but depends on the order in which we write the blocks and points. By definition, each column contains k
Is called incidence matrix of the PSD.Of course such a matrix is by no means unique, but depends on the order in which we write the blocks and points. By definition, each column contains k 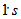 and according to the theorem 3.2.2 each row also contain
and according to the theorem 3.2.2 each row also contain 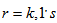 condition 2 in definition means that if we pick any two columns there are at most
condition 2 in definition means that if we pick any two columns there are at most 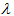 rows in which there is a 1 in both these columns. For
rows in which there is a 1 in both these columns. For 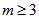 any two rows(columns) of
any two rows(columns) of 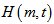 have at most one 1 in common i.e. in the same column(row). So
have at most one 1 in common i.e. in the same column(row). So 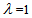 Although by theorem 3.2.1 PSD is symmetric, it does not mean that its incidence matrix should be symmetric.In an incidence matrix
Although by theorem 3.2.1 PSD is symmetric, it does not mean that its incidence matrix should be symmetric.In an incidence matrix 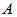 of the PSD
of the PSD 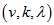 not just each row but also each column has exactly
not just each row but also each column has exactly 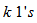 and not just every two rows but also every two columns have at most
and not just every two rows but also every two columns have at most 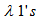 in common therefore also
in common therefore also 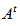 is an incidence matrix for some
is an incidence matrix for some 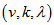 PSD, Also notice that by fisher’s in equality, the transpose of an incidence matrix design could be an incidence matrix of a design only if
PSD, Also notice that by fisher’s in equality, the transpose of an incidence matrix design could be an incidence matrix of a design only if 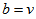 .
.3.3. Stopping Sets
- Definition: A set
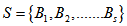 of blocks in a polygon semi design
of blocks in a polygon semi design 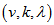 is called stopping set if
is called stopping set if 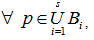
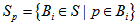 is of order at least 2. Let
is of order at least 2. Let 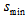 be the size of smallest non empty stopping set.
be the size of smallest non empty stopping set.3.3.1. Bounds For Stopping Sets
- Theorem 3.3.1 Let
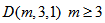 be a polygon symmetric semi design. If
be a polygon symmetric semi design. If 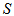 is a stopping set in
is a stopping set in 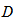 then.
then.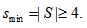 Proof As be a stopping set such that
Proof As be a stopping set such that 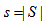 and
and 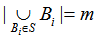 i.e. number of points is all blocks of
i.e. number of points is all blocks of 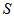 . Count the set
. Count the set 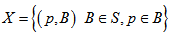 in two different ways. Since there are
in two different ways. Since there are 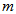 points in
points in 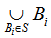 and each point lies in at least two blocks
and each point lies in at least two blocks 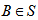 by definition of
by definition of 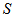 . So the total number of such pairs
. So the total number of such pairs 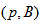 is at least
is at least 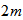 .On the other hand there are
.On the other hand there are 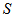 blocks in
blocks in 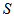 and each block containing three points so there we exactly
and each block containing three points so there we exactly 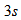 such pairs exist.
such pairs exist.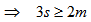 Now by inclusion exclusion principle
Now by inclusion exclusion principle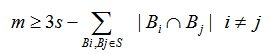
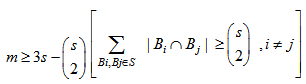 Any two blocks intersect in most two points.
Any two blocks intersect in most two points.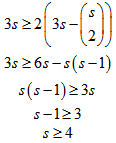 Let
Let  polygon semi design, for
polygon semi design, for  we define
we define 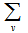 as the collection of blocks
as the collection of blocks 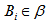 such that
such that 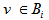 also
also 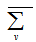 is the set
is the set 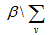 ,
,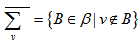 Theorem 3.3.2 Let
Theorem 3.3.2 Let 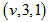 be a polygon semi design, with
be a polygon semi design, with 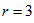 then
then 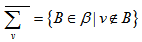 is a stopping set.Proof: Let
is a stopping set.Proof: Let 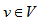 , for each
, for each 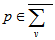 , p should be in at most 1 block of
, p should be in at most 1 block of 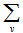 ,[by definition of polygon semi design any pair of points should be contained by at most one block]. Sine each
,[by definition of polygon semi design any pair of points should be contained by at most one block]. Sine each 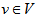 lies in exactly
lies in exactly 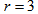 , blocks in PSD, therefore each point in
, blocks in PSD, therefore each point in 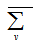 must be incident with at least 2 blocks in
must be incident with at least 2 blocks in 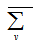 . So
. So 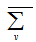 is a stopping set.Suppose by contradiction for some
is a stopping set.Suppose by contradiction for some 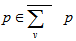 lies in two blocks of
lies in two blocks of 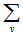 , and
, and 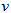 lies in more three blocks of
lies in more three blocks of 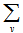 . So there is a pair of points
. So there is a pair of points 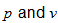 , which lies in more than one blocks of PSD, this contradicts the fact that each pair of points lies in at most one block. Hence each point in
, which lies in more than one blocks of PSD, this contradicts the fact that each pair of points lies in at most one block. Hence each point in 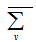 can be incident in at most one block in
can be incident in at most one block in 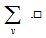 Corollary 3.3.1 In
Corollary 3.3.1 In 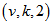 Polygon Semi Design
Polygon Semi Design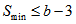 Proof: For each
Proof: For each 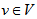 ,
, 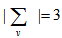
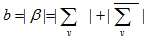
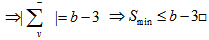
4. Conclusions
- Polygon simple graph is a new discrete structure. We worked out for some basic properties. Polygon graphs are bipartite, therefore could be used as Tanner graphs to generate low density parity check codes. A polygon semi design is again a recent development in combinatorial mathematics. Some results are proved on these designs. The bounds proved for stopping sets, are to be used as a performance indicator for the LDPC codes defined on polygon semi designs, these codes are widely used for error deduction and correction.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML