Atikur Rahman Baizid1, 2, Md. Shah Alam2
1Department of Business Administration, Leading University, Sylhet, 3100, Bangladesh
2Department of Physics, Shahjalal University of Science and Technology, Sylhet, 3114, Bangladesh
Correspondence to: Atikur Rahman Baizid, Department of Business Administration, Leading University, Sylhet, 3100, Bangladesh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
It is obvious that Lorentz transformation is the starting point of Relativistic mechanics. There are different types of Lorentz transformations such as Special, Most general, Mixed number, Geometric product, and Quaternion Lorentz transformations. To study relativistic mechanics, we must need to know the properties of different types of Lorentz transformations. In this paper we have studied reciprocal property, associative property, isotropic property and group property of the above Lorentz transformations.
Keywords:
Special Lorentz Transformation, Most General Lorentz Transformation, Mixed Number Lorentz Transformation, Geometric Product Lorentz Transformation, Reciprocal Property, Associative Property , Isotropic Property, Group Property
Cite this paper: Atikur Rahman Baizid, Md. Shah Alam, Properties of Different Types of Lorentz Transformations, American Journal of Mathematics and Statistics, Vol. 3 No. 3, 2013, pp. 105-123. doi: 10.5923/j.ajms.20130303.03.
1. Introduction
In most treatments on special relativity, the line of motion is aligned with the x-axis. This is a natural choice because in such a situation the 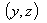 coordinates are invariant under the Lorentz transformations. However; it is of interest to study the case when the line of motion does not coincide with any of the coordinate axes. Practical instances of such a situation are an airplane during landing or take off. The ground at the airfield has a natural coordinate system with the x-axis parallel to the ground, whereas the airplane ascends or descends at an angle with ground. For this reason we need to study the properties of different types Lorentz transformations where the line of action is along x-axis as well as along any arbitrary line. We have studied the Reciprocal property, Associative property, Isotropic property, Group property of different types of Lorentz transformations.
coordinates are invariant under the Lorentz transformations. However; it is of interest to study the case when the line of motion does not coincide with any of the coordinate axes. Practical instances of such a situation are an airplane during landing or take off. The ground at the airfield has a natural coordinate system with the x-axis parallel to the ground, whereas the airplane ascends or descends at an angle with ground. For this reason we need to study the properties of different types Lorentz transformations where the line of action is along x-axis as well as along any arbitrary line. We have studied the Reciprocal property, Associative property, Isotropic property, Group property of different types of Lorentz transformations.
1.1. Special Lorentz Transformation
Consider two inertial frames of Reference  and
and 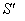 where the frame
where the frame 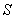 is at rest and the frame
is at rest and the frame 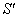 is moving along X-axis with velocity V with respect to
is moving along X-axis with velocity V with respect to 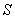 frame. The space and time coordinates of
frame. The space and time coordinates of 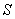 and
and 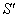 are (x, y, z, t) and (x′, y′, z′, t′) respectively. The relation between the coordinates of
are (x, y, z, t) and (x′, y′, z′, t′) respectively. The relation between the coordinates of 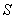 and
and 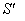 is called Special Lorentz transformation which can be written as [1]
is called Special Lorentz transformation which can be written as [1]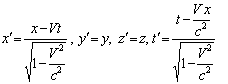 | (1) |
And 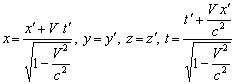 | (2) |
1.2. Most General Lorentz Transformation
When the velocity 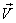 of
of 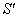 with respect to
with respect to 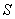 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 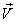 has three components Vx, Vy and Vz. Then the relation between the coordinates of
has three components Vx, Vy and Vz. Then the relation between the coordinates of 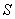 and
and 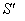 is called Most general Lorentz transformation which can be written as [2]
is called Most general Lorentz transformation which can be written as [2]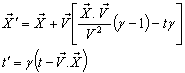 | (3) |
and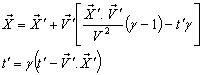 | (4) |
Where ,
,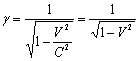 in unit of C
in unit of C
1.3. Mixed Number Lorentz Transformation
In the case of Most General Lorentz transformation, the velocity 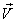 of S' with respect to
of S' with respect to  is not along X-axis; i.e., the velocity
is not along X-axis; i.e., the velocity 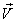 has three components, Vx, Vy, and Vz. Let in this case Z and Z' be the space parts in
has three components, Vx, Vy, and Vz. Let in this case Z and Z' be the space parts in  and S' frames, respectively. Then using the mixed product
and S' frames, respectively. Then using the mixed product 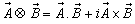 , Mixed number Lorentz transformations [3 – 6] can be written as
, Mixed number Lorentz transformations [3 – 6] can be written as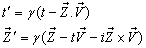 | (5) |
And 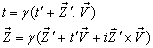 | (6) |
1.4. Geometric Product Lorentz Transformation
In this case the velocity 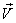 of S' with respect to
of S' with respect to 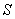 also has three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case
also has three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case 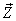 and
and 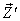 be the space parts in
be the space parts in 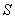 and S' frames respectively. Then using geometric product of two vectors
and S' frames respectively. Then using geometric product of two vectors 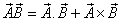 the geometric product Lorentz transformation [7, 8] can be written as
the geometric product Lorentz transformation [7, 8] can be written as 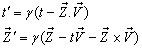 | (7) |
And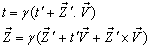 | (8) |
1.5. Quaternion Lorentz Transformation
In this case the velocity 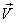 of S' with respect to
of S' with respect to 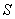 has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case
has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case 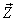 and
and 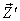 be the space parts in
be the space parts in 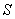 and S' frames respectively. Then using quaternion product
and S' frames respectively. Then using quaternion product 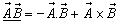 the Quaternion Lorentz transformation [9-12] can be written as
the Quaternion Lorentz transformation [9-12] can be written as 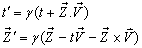 | (9) |
And 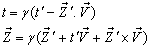 | (10) |
2. Reciprocal Property of Different Types of Lorentz Transformations
2.1. Reciprocal Property of Special Lorentz Transformation
The velocity addition formula for special Lorentz transformation [13] can beWritten as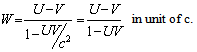 | (11) |
If we replace U by P where 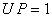 then
then 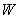 will be change to
will be change to 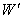 where
where 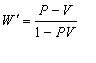 Reciprocal property demands that if
Reciprocal property demands that if 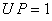 then
then  Now,
Now,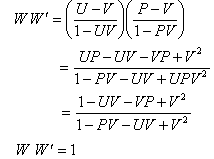 | (12) |
Consequently, special Lorentz transformation satisfies the reciprocal property.
2.2. Reciprocal Property of Most General Lorentz Transformation
From the transformation equations of addition of velocities of most general Lorentz transformation [14] we have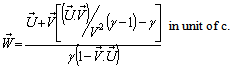 | (13) |
If we replace 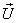 by
by 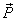 where
where 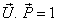 then
then 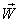 will be change to
will be change to 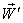 where
where 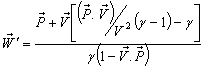 Reciprocal property demands that if
Reciprocal property demands that if 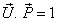 then
then 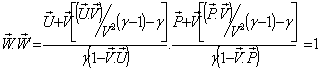 Now,
Now,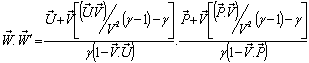 Can be written as
Can be written as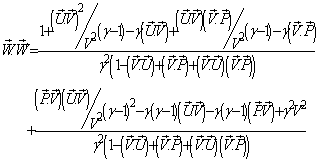 So,
So, 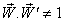 | (14) |
Consequently, the most general Lorentz transformation does not satisfy the reciprocal property.
2.3. Reciprocal Property of Mixed Number Lorentz Transformation
From the transformation equations of addition of velocities of mixed number Lorentz transformation [14] we have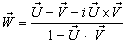 | (15) |
If we replace 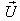 by
by 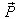 where
where 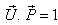 then
then 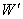 will be change to
will be change to 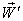 where
where 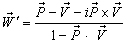 Reciprocal property demands that if
Reciprocal property demands that if 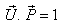 then
then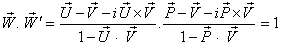 Now,
Now,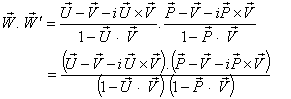 can be written as
can be written as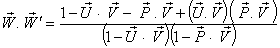
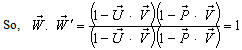 | (16) |
SimilarlyIf we replace 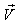 by
by 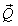 where
where 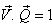 then
then 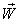 will be change to
will be change to 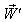 where
where 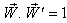 Consequently, Mixed number Lorentz transformation satisfies the reciprocal property.
Consequently, Mixed number Lorentz transformation satisfies the reciprocal property.
2.4. Reciprocal Property of Geometric Product Lorentz Transformation
From the transformation equations of addition of velocities of geometric product Lorentz transformation [14] we have,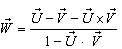 | (17) |
If we replace 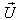 by
by 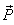 where
where 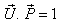 then
then 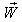 will be change to
will be change to 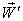 where
where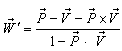 Reciprocal property demands that if
Reciprocal property demands that if 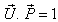 then
then 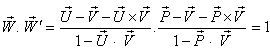 Now,
Now, 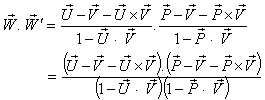 Can be written as
Can be written as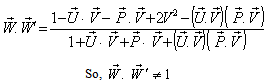 | (18) |
Consequently, geometric product Lorentz transformation does not satisfy the reciprocal property.
2.5. Reciprocal Property of Quaternion Lorentz Transformation
From the transformation equations of addition of velocities of Quaternion Lorentz transformation [14] we have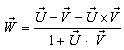 | (19) |
If we replace 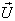 by
by 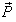 where
where 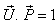 then
then 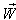 will be change to
will be change to 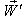 where
where 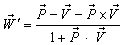 Reciprocal property demands that if
Reciprocal property demands that if 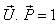 then
then 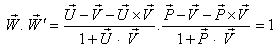 Now,
Now, 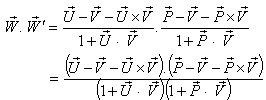 Can be written as
Can be written as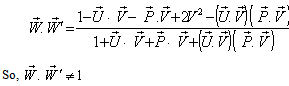 | (20) |
Consequently, the Quaternion Lorentz transformation does not satisfy the reciprocal property.
3. Associative Property of Different Types of Lorentz Transformations
Consider three inertial frames of reference S ,  ,
, and
and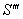 where the frame S is at rest and the frame
where the frame S is at rest and the frame 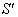 is moving with velocity
is moving with velocity 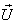 with respect to S,
with respect to S, 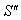 is moving with velocity
is moving with velocity 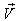 with respect to
with respect to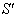 ,
, 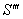 is moving with velocity
is moving with velocity 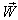 respect to
respect to 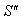 then associative property says that
then associative property says that 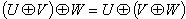 [Fig-1]. We are going to discuss the associative property of different Lorentz transformations in unit of c. Let
[Fig-1]. We are going to discuss the associative property of different Lorentz transformations in unit of c. Let 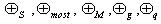 are the symbols of the Lorentz sum of Special, Most general, Mixed number, geometric product, and Quaternion product Lorentz transformations respectively.
are the symbols of the Lorentz sum of Special, Most general, Mixed number, geometric product, and Quaternion product Lorentz transformations respectively.
3.1. Associative Property of Special Lorentz Transformation
The velocity addition formula for special Lorentz transformation [13] can be written as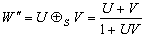 | (21) |
Now , if 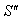 moves with velocity
moves with velocity 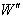 with respect to S , then according to the velocity addition formula for special Lorentz transformation [13] can be written as
with respect to S , then according to the velocity addition formula for special Lorentz transformation [13] can be written as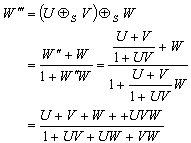 | (22) |
Again, Let 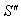 moves with velocity V with respect to
moves with velocity V with respect to 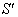 and
and 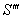 moves with velocity W with respect to
moves with velocity W with respect to 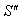 then according to the velocity addition formula for the Special Lorentz transformation [13] the resultant velocity of V and W can be written as
then according to the velocity addition formula for the Special Lorentz transformation [13] the resultant velocity of V and W can be written as 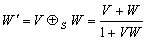 | (23) |
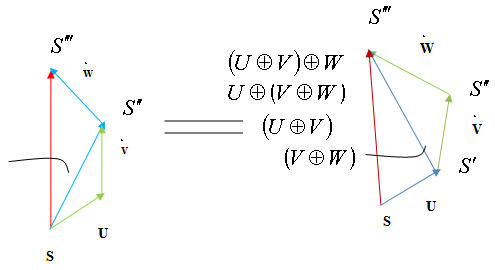 | Figure 1. Associative Property of Lorentz transformations |
Finally, let  moves with velocity U with respect to S and
moves with velocity U with respect to S and  moves with velocity
moves with velocity  with respect to
with respect to 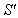 then the resultant velocity [13] of U and
then the resultant velocity [13] of U and 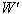 can be written as
can be written as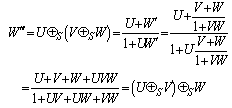 | (24) |
Hence,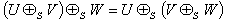 | (25) |
Consequently, Special Lorentz transformation satisfies the Associative property.
3.2. Associative Property of Most General Lorentz Transformation
The velocity addition formula for most general Lorentz transformation [14] can be written as 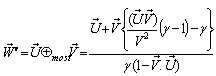 | (26) |
Let us consider 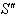 moves with velocity
moves with velocity 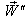 with respect to S and
with respect to S and 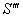 moves with velocity
moves with velocity 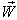 respect to
respect to 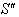 then according to the velocity addition formula for most general Lorentz transformation [14] can be written as
then according to the velocity addition formula for most general Lorentz transformation [14] can be written as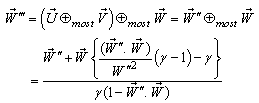 Substituting the value of
Substituting the value of 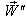 we have
we have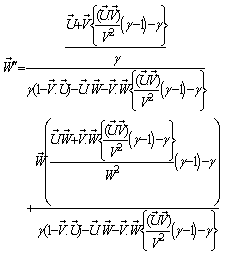 | (27) |
Again, Let  moves with velocity
moves with velocity 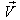 with respect to
with respect to 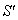 and
and 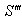 moves with velocity
moves with velocity 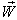 with respect to
with respect to 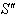 then according to the velocity addition formula for most general Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for most general Lorentz transformation [14] the resultant velocity of 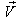 and
and 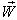 can be written as
can be written as 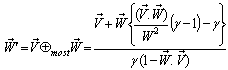 | (28) |
Finally, let 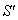 moves with velocity
moves with velocity 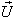 with respect to S and
with respect to S and 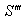 moves with velocity
moves with velocity 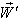 with respect to
with respect to 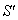 then the resultant velocity [14] of
then the resultant velocity [14] of 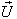 and
and 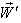 can be written as
can be written as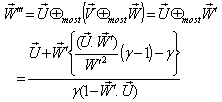 | (29) |
Substituting the value of 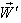 the above expression can be written as
the above expression can be written as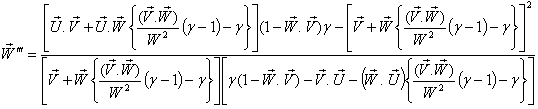 | (30) |
Hence, | (31) |
Consequently, the Most general Lorentz transformation does not satisfy the Associative property.
3.3. Associative Property of Mixed Number Lorentz Transformation
The velocity addition formula for mixed Number Lorentz transformation [14] can be written as 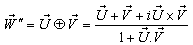 | (32) |
Now, if 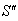 moves with velocity
moves with velocity 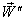 with respect to S and
with respect to S and 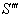 moves with velocity
moves with velocity 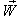 respect to
respect to 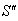 then according to the velocity addition formula for mixed number Lorentz transformation [14] can be written as
then according to the velocity addition formula for mixed number Lorentz transformation [14] can be written as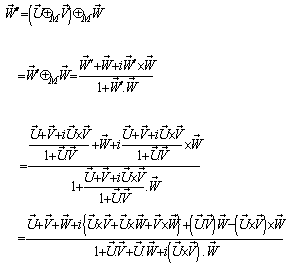 | (33) |
Again, Let 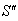 moves with velocity
moves with velocity 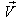 with respect to
with respect to 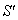 and
and 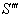 moves with velocity
moves with velocity 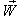 with respect to
with respect to 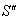 then according to the velocity addition formula for mixed number Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for mixed number Lorentz transformation [14] the resultant velocity of 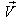 and
and 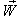 can be written as
can be written as 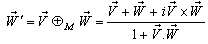 | (34) |
Finally, let 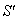 moves with velocity
moves with velocity 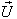 with respect to S and
with respect to S and 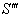 moves with velocity
moves with velocity 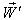 with respect to
with respect to 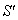 then using (34) the resultant velocity [14] of
then using (34) the resultant velocity [14] of 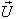 and
and 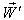 can be written as
can be written as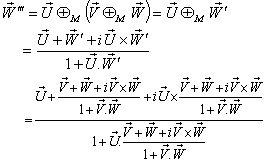 | (35) |
Can be written as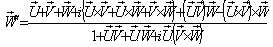 Hence,
Hence,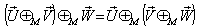 | (36) |
Consequently, mixed number Lorentz transformation satisfies the Associative property.
3.4. Associative Property of Geometric Product Lorentz Transformation
The velocity addition formula for geometric product Lorentz transformation [14] can be written as 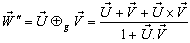 | (37) |
Now, if 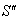 moves with velocity
moves with velocity 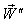 with respect to S and
with respect to S and 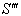 moves with velocity
moves with velocity 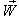 respect to
respect to 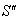 then according to the velocity addition formula for geometric product Lorentz transformation [14] can be written as
then according to the velocity addition formula for geometric product Lorentz transformation [14] can be written as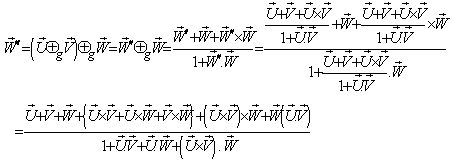 | (38) |
Again, Let 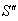 moves with velocity
moves with velocity 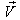 with respect to
with respect to 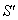 and
and 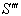 moves with velocity
moves with velocity 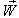 with respect to
with respect to 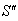 then according to the velocity addition formula for the Geometric product Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for the Geometric product Lorentz transformation [14] the resultant velocity of 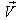 and
and 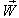 can be written as
can be written as 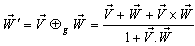 | (39) |
Finally, let 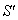 moves with velocity
moves with velocity 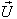 with respect to S and
with respect to S and 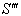 moves with velocity
moves with velocity 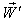 with respect to
with respect to 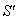 then using (39) the resultant velocity [14] of
then using (39) the resultant velocity [14] of 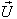 and
and 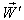 can be written as
can be written as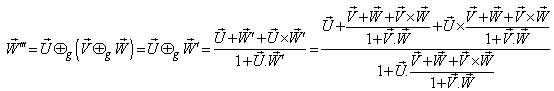 can be written as
can be written as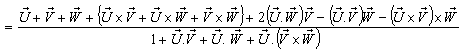 | (40) |
Hence,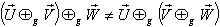 | (41) |
Consequently, geometric product Lorentz transformation does not satisfy the Associative property.
3.5. Associative Property of Quaternion Lorentz Transformation
The velocity addition formula for Quaternion Lorentz transformation [14] can be written as 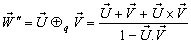 | (42) |
Now, if 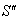 moves with velocity
moves with velocity 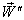 with respect to S and
with respect to S and 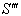 moves with velocity
moves with velocity 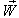 respect to
respect to 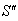 then according to the velocity addition formula for the Quaternion Lorentz transformation [14] can be written as
then according to the velocity addition formula for the Quaternion Lorentz transformation [14] can be written as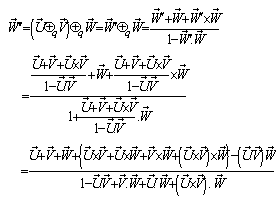 | (43) |
Again, Let 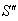 moves with velocity
moves with velocity 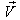 with respect to
with respect to 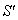 and
and 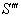 moves with velocity
moves with velocity 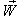 with respect to
with respect to 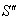 then according to the velocity addition formula for the Quaternion Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for the Quaternion Lorentz transformation [14] the resultant velocity of 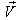 and
and 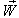 can be written as
can be written as 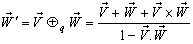 | (44) |
Finally, let 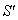 moves with velocity
moves with velocity 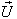 with respect to S and
with respect to S and 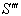 moves with velocity
moves with velocity 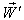 with respect to
with respect to 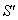 then using (44) the resultant velocity [14] of
then using (44) the resultant velocity [14] of 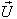 and
and 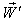 can be written as
can be written as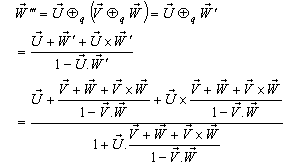 | (45) |
Can be written as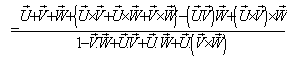 Hence,
Hence,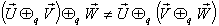 | (46) |
Consequently, Quaternion Lorentz transformation does not satisfy the Associative property.It can be easily shown that the above Lorentz Transformations satisfy the associative property if Vy=0 and Vz =0, reducing these to Special Lorentz Transformation
4. Isotropic Property of Lorentz Transformations
Consider three inertial frames of Reference 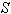 ,
, 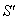 and
and 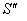 where
where 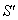 moves with velocity
moves with velocity 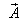 with respect to
with respect to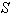 and
and 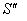 moves with velocity
moves with velocity 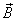 with respect to
with respect to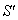 . If
. If 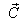 be the velocity of
be the velocity of  with respect to
with respect to .
.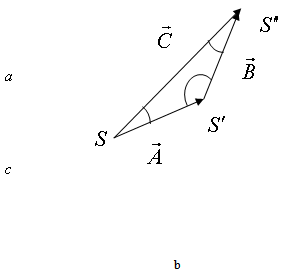 | Figure 2. Isotropic property of Lorentz Transformations |
If a, b and c are the three angles of the triangle , then according to Lorentz sum we can write
, then according to Lorentz sum we can write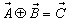 | (47) |
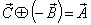 | (48) |
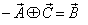 | (49) |
and their product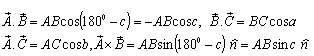 Now the isotropic property demands that if
Now the isotropic property demands that if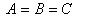 then
then 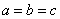
4.1. Isotropic Property of Special Lorentz Transformation
For special Lorentz transformation, there will be no option to make a triangle. So, isotropic property is not applicable for special Lorentz transformation.
4.2. Isotropic Property of Most General Lorentz Transformation
The velocity addition formula for most general Lorentz transformation [14] can be written as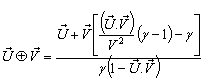 | (50) |
Using equation (47) and (50) we can write (taking c = 1)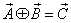
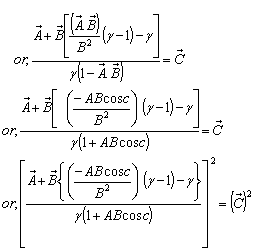
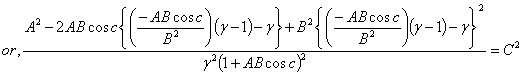 | (51) |
Putting A = B = C in equation (51) we get 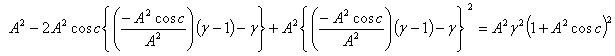
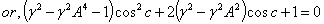
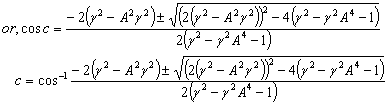 | (52) |
Using equation (48) and (50) we can write (taking c = 1)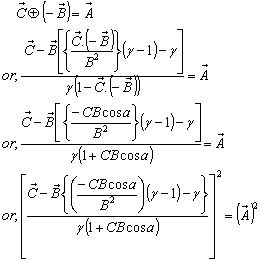
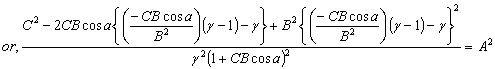 | (53) |
Putting A = B = C in equation (53) we get 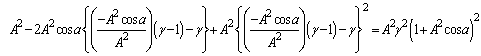
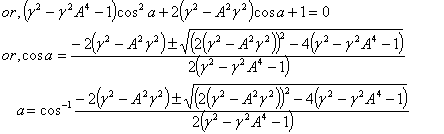 | (54) |
Using equation (49) and (50) we can write (taking c = 1) 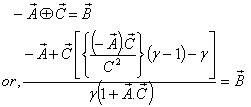
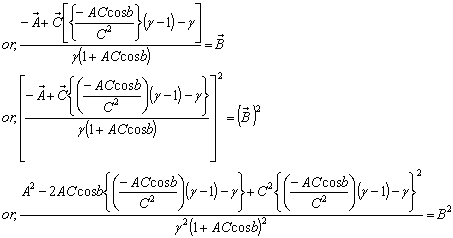 | (55) |
Putting A = B = C in equation (55) we get 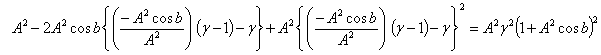
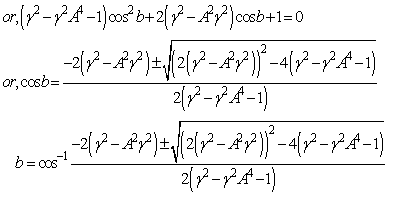 | (56) |
Hence, from equations (52), (54) and (56) we have 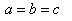 Hence, most general Lorentz transformation satisfies the isotropic property
Hence, most general Lorentz transformation satisfies the isotropic property
4.3. Isotropic Property of Mixed Number Lorentz Transformation
The velocity addition formula for mixed number Lorentz transformation [14] can be written as 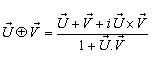 | (57) |
Using equation (47) and (57) we can write (taking c = 1)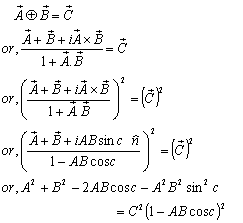 | (58) |
Putting A = B = C in equation (22) we get 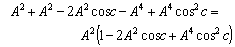
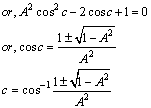 | (59) |
Using equation (48) and (57) we can write (taking c = 1) 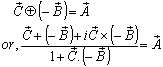
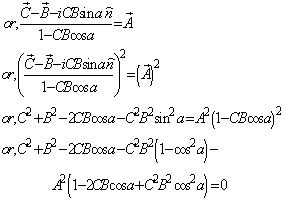 | (60) |
Putting A = B = C in equation (60) we get 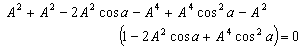
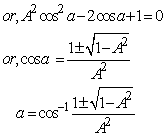 | (61) |
Using equation (49) and (57) we can write (taking )
)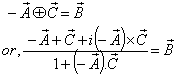
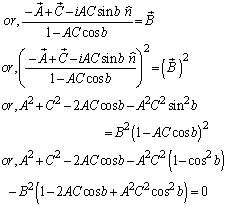 | (62) |
Putting A = B = C in equation (26) we get 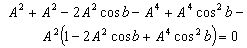
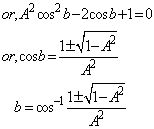 | (63) |
Hence, from equations (59), (61) and (63) we have  Hence, Mixed number Lorentz transformation satisfies the isotropic property.
Hence, Mixed number Lorentz transformation satisfies the isotropic property.
4.4. Isotropic Property of Geometric Product Lorentz Transformation
The velocity addition formula for Geometric product Lorentz transformation [14] can be written as 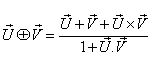 | (64) |
Using equation (47) and (64) we can write (taking c = 1)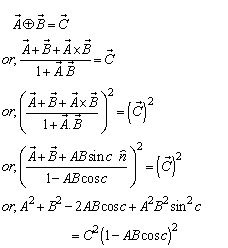 | (65) |
Putting A = B = C in equation (65) we get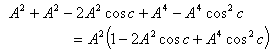
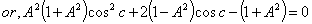
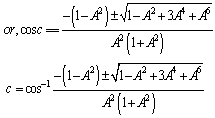 | (66) |
Using equation (48) and (64) we can write (taking c = 1) 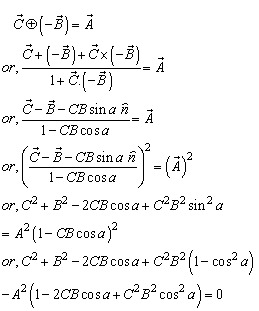 | (67) |
Putting A = B = C in equation (67) we get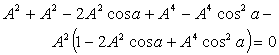
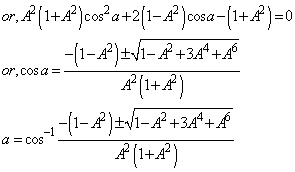 | (68) |
Using equation (49) and (64) we can write (taking c = 1)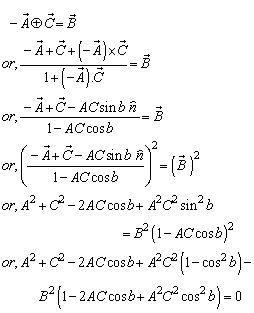 | (69) |
Putting A = B = C in equation (69) we get 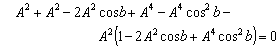
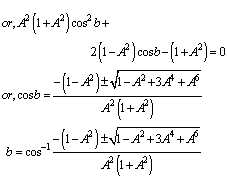 | (70) |
Hence, from equations (66), (68) and (70) we have 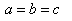 Hence, geometric product Lorentz Transformation satisfies the isotropic property
Hence, geometric product Lorentz Transformation satisfies the isotropic property
4.5. Isotropic Property of Quaternion Lorentz Transformation
The velocity addition formula for Quaternion Lorentz transformation [14] can be written as 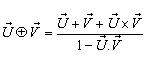 | (71) |
Using equation (47) and (71) we can write (taking c = 1)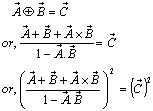
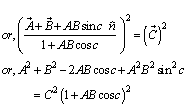 | (72) |
Putting A = B = C in equation (72) we get 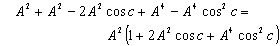
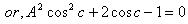
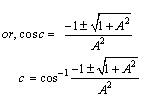 | (73) |
Using equation (48) and (71) we can write (taking c = 1) 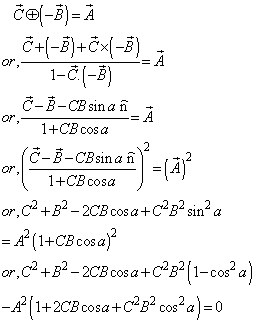 | (74) |
Putting A = B = C in equation (74) we get 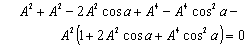
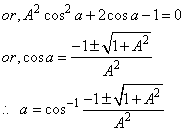 | (75) |
Using equation (49) and (71) we can write (taking c = 1) 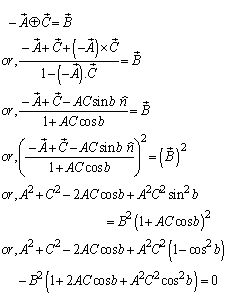 | (76) |
Putting A = B = C in equation (76) we get 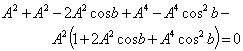
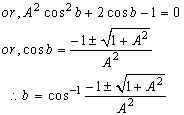 | (77) |
Hence, from equations (73), (75) and (77) we have 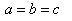 Hence, Quaternion Lorentz transformation satisfies the isotropic property.
Hence, Quaternion Lorentz transformation satisfies the isotropic property.
5. Group Property of Lorentz Transformations
The result of two Lorentz transformations is itself a Lorentz transformation [13]
5.1. Group Property of Special Lorentz Transformation
Consider three inertial frames of reference 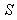 ,
, 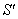 and
and 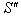 where
where 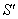 has relative velocity
has relative velocity 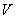 with respect to
with respect to 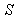 along positive x-axis and
along positive x-axis and 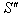 has relative velocity
has relative velocity 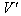 with respect to
with respect to 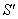 along the same direction as shown in fig.1. According to special Lorentz transformation we get
along the same direction as shown in fig.1. According to special Lorentz transformation we get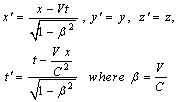 | (78) |
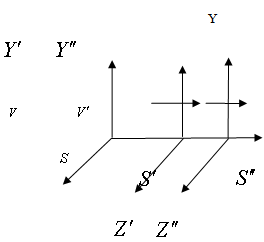 | Figure 3. Special Lorentz Transformations |
Similarly if the origins in 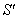 and
and 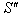 coincide at
coincide at 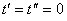 the space and time co-ordinates in
the space and time co-ordinates in 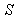 and
and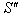 related as
related as 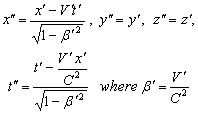 | (79) |
Suppose,  be the resultant velocity of
be the resultant velocity of 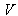 and
and 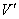 then from the velocity addition formula [14] we get
then from the velocity addition formula [14] we get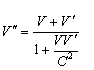 | (80) |
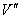 is the velocity of system
is the velocity of system 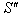 relative to
relative to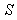 . To prove this result we have to show that
. To prove this result we have to show that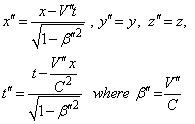 | (81) |
Now, 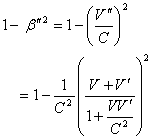 Can be written as
Can be written as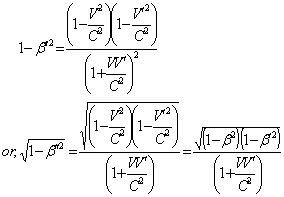
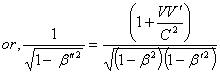 | (82) |
Now using (15) 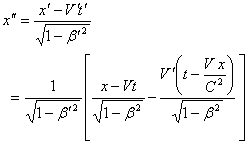 Can be written as
Can be written as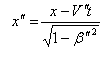 So,
So, 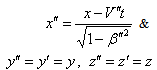 | (83) |
Again, from equation (82)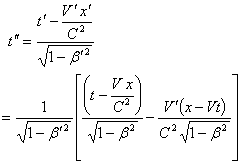 Can be written as
Can be written as 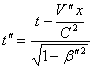 Thus the result of two Lorentz transformations is itself a Lorentz transformation. Hence Special Lorentz transformations form a group.
Thus the result of two Lorentz transformations is itself a Lorentz transformation. Hence Special Lorentz transformations form a group.
5.2. Group Property of Most General Lorentz Transformation
Consider three inertial frames of Reference 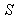 ,
, 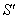 and
and 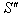 where
where 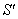 moves with velocity
moves with velocity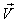 with respect to
with respect to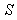 and
and 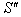 moves with velocity
moves with velocity 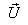 with respect to
with respect to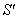 . If
. If 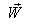 be the velocity of
be the velocity of 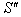 with respect to
with respect to 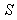
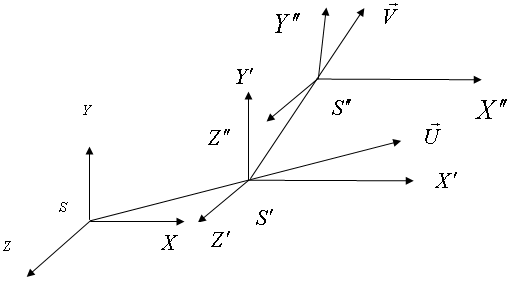 | Figure 4. Most General Lorentz Transformation |
So the relation between the co-ordinates  in
in  and
and  in
in  can be expressed by most general Lorentz transformation by
can be expressed by most general Lorentz transformation by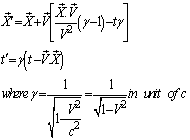 | (84) |
Similarly, the relation between the co-ordinates  in
in  and
and 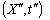 in
in 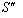 can be expressed by most general Lorentz transformation by
can be expressed by most general Lorentz transformation by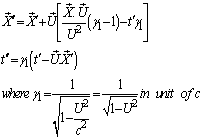 | (85) |
Similarly, the relation between the co-ordinates 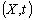 in
in 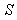 and
and 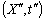 in
in 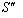 can be expressed by most general Lorentz transformation by
can be expressed by most general Lorentz transformation by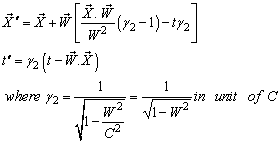 | (86) |
From the velocity addition formula for Most General Lorentz transformation [14] we can write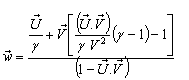 Now we have from (85)
Now we have from (85)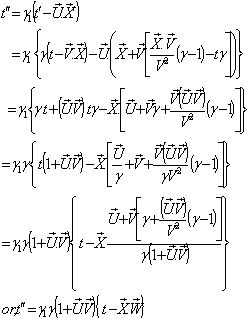 Where
Where 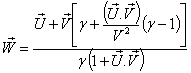 Now we have to show
Now we have to show 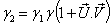 We know
We know 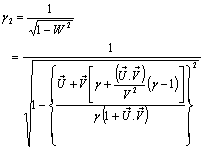 Can be written as
Can be written as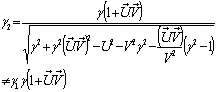 Hence, the time part of the Most General Lorentz transformation does not satisfy the group property.Again from equation (85)
Hence, the time part of the Most General Lorentz transformation does not satisfy the group property.Again from equation (85)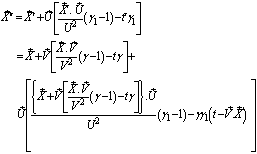 Which can be written as
Which can be written as 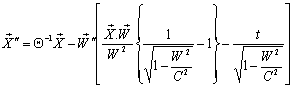 Where the operator
Where the operator 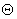 in general is different from the unit operator.
in general is different from the unit operator. 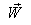 is the velocity of the system
is the velocity of the system 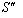 relative to
relative to 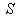 and
and 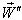 is the velocity of the system
is the velocity of the system 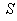 relative to
relative to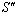 .We get
.We get 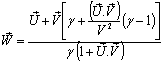 and
and 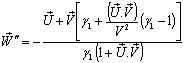 Now
Now 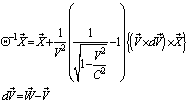 | (87) |
Hence we have 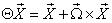
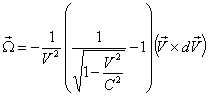 UThe rotation operator thus represents an infinitesimal rotation around the direction of the vector
UThe rotation operator thus represents an infinitesimal rotation around the direction of the vector 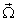 [3]Hence, most general Lorentz transformation does not satisfy the group property without rotation
[3]Hence, most general Lorentz transformation does not satisfy the group property without rotation
5.3. Group Property of Mixed Number Lorentz Transformation
Figure-2 describes that three inertial frames of reference 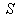 ,
, 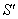 and
and 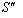 where
where 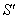 moves with velocity
moves with velocity 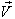 with respect to
with respect to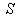 and
and 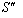 moves with velocity
moves with velocity 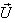 with respect to
with respect to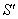 .If
.If 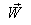 be the velocity of
be the velocity of 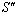 with respect to
with respect to 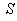 then the relation between the co-ordinates
then the relation between the co-ordinates 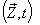 in
in 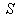 and
and 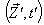 in
in 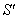 can be expressed by mixed number Lorentz transformation by
can be expressed by mixed number Lorentz transformation by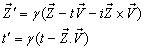 | (88) |
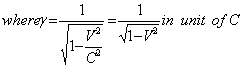 Similarly, the relation between the co-ordinates
Similarly, the relation between the co-ordinates 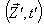 in
in 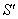 and
and 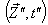 in
in 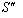 can be expressed by Mixed Number Lorentz transformation by
can be expressed by Mixed Number Lorentz transformation by 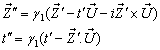 | (89) |
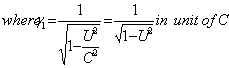 Similarly, the relation between the co-ordinates
Similarly, the relation between the co-ordinates 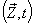 in
in 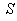 and
and 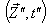 in
in 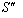 can be expressed by mixed Number Lorentz transformation by
can be expressed by mixed Number Lorentz transformation by 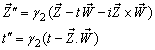 | (90) |
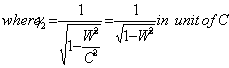 The velocity addition formula for mixed Number Lorentz transformation [14] can be written as
The velocity addition formula for mixed Number Lorentz transformation [14] can be written as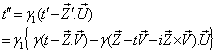 | (91) |
Now from equation (89) we can write 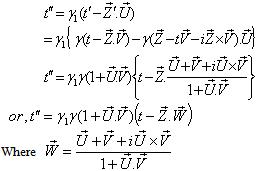 | (92) |
Again from equation (91) we can write 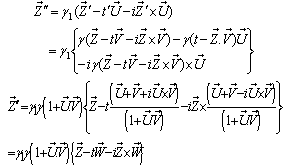 Where
Where 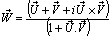 Now we have to show that
Now we have to show that 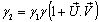
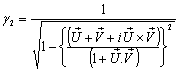
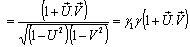 Hence,
Hence, 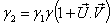 Therefore, mixed Number Lorentz transformation satisfies the group property
Therefore, mixed Number Lorentz transformation satisfies the group property
5.4. Group Property of Geometric Product Lorentz Transformation
Figure-2 describes that three inertial frames of Reference  ,
,  and
and 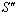 where
where 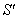 moves with velocity
moves with velocity 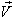 with respect to
with respect to and
and 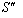 moves with velocity
moves with velocity 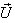 with respect to
with respect to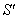 .If
.If 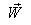 be the velocity of
be the velocity of 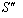 with respect to
with respect to 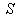 then the relation between the co-ordinates
then the relation between the co-ordinates 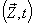 in
in 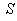 and
and 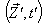 in
in 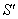 can be expressed by geometric product Lorentz transformation by
can be expressed by geometric product Lorentz transformation by 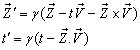 | (93) |
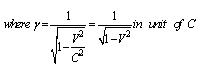 Similarly, the relation between the co-ordinates
Similarly, the relation between the co-ordinates 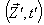 in
in 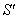 and
and 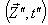 in
in 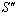 can be expressed by geometric product Lorentz transformation by
can be expressed by geometric product Lorentz transformation by 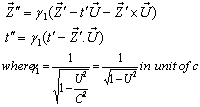 | (94) |
Similarly, the relation between the co-ordinates 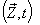 in
in 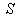 and
and 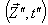 in
in 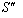 can be expressed by geometric Product Lorentz transformation by
can be expressed by geometric Product Lorentz transformation by 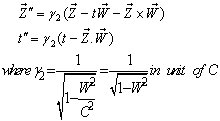 | (95) |
The velocity addition formula for geometric product Lorentz transformation [14] can be written as 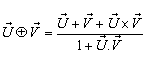 | (96) |
Now from equation (94) we can write 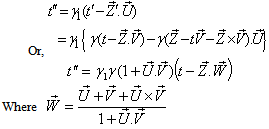 Again from equation (94) we can write
Again from equation (94) we can write 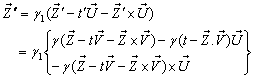
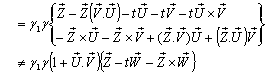 Where
Where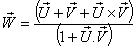 Now we have to show that
Now we have to show that 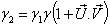
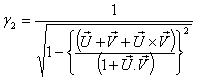
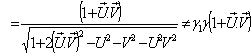 Therefore, Geometric Product Lorentz transformation does not satisfy the isotropic property
Therefore, Geometric Product Lorentz transformation does not satisfy the isotropic property
5.5. Group Property of Quaternion Product Lorentz Transformation
Figure-2 describes that three inertial frames of Reference  ,
,  and
and  where
where 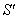 moves with velocity
moves with velocity 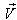 with respect to
with respect to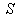 and
and 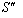 moves with velocity
moves with velocity 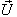 with respect to
with respect to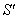 .If
.If 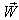 be the velocity of
be the velocity of 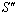 with respect to
with respect to 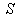 then the relation between the co-ordinates
then the relation between the co-ordinates 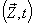 in
in 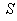 and
and 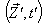 in
in 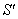 can be expressed by Quaternion Product Lorentz transformation by
can be expressed by Quaternion Product Lorentz transformation by 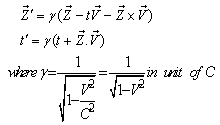 | (97) |
Similarly, the relation between the co-ordinates 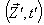 in
in 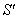 and
and 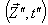 in
in 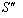 can be expressed by Quaternion Product Lorentz transformation by
can be expressed by Quaternion Product Lorentz transformation by 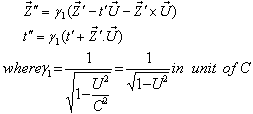 | (98) |
Similarly, the relation between the co-ordinates 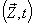 in
in 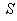 and
and 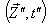 in
in 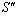 can be expressed by Quaternion Product Lorentz transformation by
can be expressed by Quaternion Product Lorentz transformation by 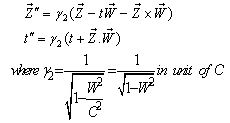 | (99) |
The velocity addition formula for Quaternion Product Lorentz transformation [14] can be written as 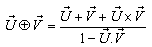 | (100) |
Now from equation (98) we can write 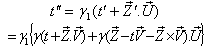 Or,
Or, 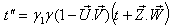 Where
Where 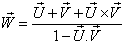 Again from equation (98) we can write
Again from equation (98) we can write 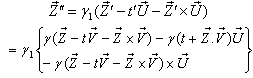 Can be written as
Can be written as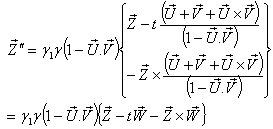 Where
Where 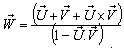 Now we have to show that
Now we have to show that 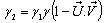
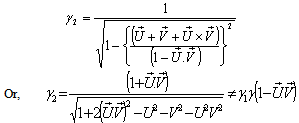 Therefore, Quaternion Product Lorentz transformation does not satisfy the group property
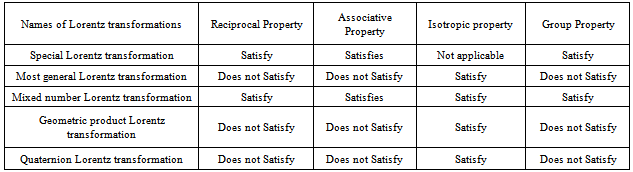
Therefore, Quaternion Product Lorentz transformation does not satisfy the group propertyTable 1. Comparison of the properties of different Lorentz transformations
 |
| |
|
6. Conclusions
We have discussed different properties of different Lorentz transformations and obtained that special and mixed number Lorentz transformations satisfy the reciprocal property. Most general, geometric product and Quaternion Lorentz transformations do not satisfy the reciprocal property. Special and mixed number Lorentz transformations satisfy Associative property but the most general, geometric product and Quaternion Lorentz transformations do not satisfy the Associative property. Isotropic property is not applicable for special Lorentz transformation. Most general, mixed number, geometric product and Quaternion Lorentz transformations satisfy the isotropic property. Special and mixed number Lorentz transformations satisfy the group property. Most general, geometric product and Quaternion Lorentz transformations do not satisfy the group property.
References
| [1] | Resnick, Robert. Introduction to special relativity, Wiley Eastern Limited New age international limited - 1994 |
| [2] | Moller C. The Theory of Relativity Oxford University Press-1972 |
| [3] | Alam, M.S. 2000. Study of Mixed Number, Proc. Pakistan Acad. of Sci. 37(1):119-122. |
| [4] | Alam, M.S. 2001. Mixed product of vectors, Journal of Theoretics, 3(4). http://www.journaloftheoretics.com/ |
| [5] | Alam, M.S. 2003. Comparative study of mixed product and quaternion product, Indian J. Physics A 77: 47-49. |
| [6] | Alam, M.S. 2001. Mixed product of vectors, Journal of Theoretics, 3(4). http://www.journaloftheoretics.com/ |
| [7] | Datta, B.K., De Sabbata V. and Ronchetti L. 1998. Quantization of gravity in real space time, Il Nuovo Cimento, 113B. |
| [8] | Datta, B.K., Datta R. 1998. Einstein field equations in spinor formalism, Foundations of Physics letters, 11, 1. |
| [9] | Kyrala, A. 1967. Theoretical Physics, W.B. Saunders Company. Philadelphia & London, Toppan Company Limited. Tokyo, Japan. |
| [10] | http://mathworld.wolfram.com/Quaternion.html |
| [11] | http://www.cs.appstate.edu/~sjg/class/3110/mathfestalg2000/quaternions1.html |
| [12] | Alam, M.S. 2003. Different types of product of vectors, NewsBull.Cal.Math.Soc. 26(1,2 & 3) 21-24. |
| [13] | Satya Prokash. Relativistic Mechanics, Pragati Prakashan-2000, India. |
| [14] | Md. Shah Alam and Khurshida Begum. Different Types of Lorentz Transformations, Jahangirnagar Physics studies-2009. |

 coordinates are invariant under the Lorentz transformations. However; it is of interest to study the case when the line of motion does not coincide with any of the coordinate axes. Practical instances of such a situation are an airplane during landing or take off. The ground at the airfield has a natural coordinate system with the x-axis parallel to the ground, whereas the airplane ascends or descends at an angle with ground. For this reason we need to study the properties of different types Lorentz transformations where the line of action is along x-axis as well as along any arbitrary line. We have studied the Reciprocal property, Associative property, Isotropic property, Group property of different types of Lorentz transformations.
coordinates are invariant under the Lorentz transformations. However; it is of interest to study the case when the line of motion does not coincide with any of the coordinate axes. Practical instances of such a situation are an airplane during landing or take off. The ground at the airfield has a natural coordinate system with the x-axis parallel to the ground, whereas the airplane ascends or descends at an angle with ground. For this reason we need to study the properties of different types Lorentz transformations where the line of action is along x-axis as well as along any arbitrary line. We have studied the Reciprocal property, Associative property, Isotropic property, Group property of different types of Lorentz transformations. and
and  where the frame
where the frame 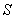 is at rest and the frame
is at rest and the frame 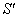 is moving along X-axis with velocity V with respect to
is moving along X-axis with velocity V with respect to 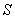 frame. The space and time coordinates of
frame. The space and time coordinates of 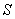 and
and 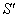 are (x, y, z, t) and (x′, y′, z′, t′) respectively. The relation between the coordinates of
are (x, y, z, t) and (x′, y′, z′, t′) respectively. The relation between the coordinates of 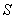 and
and 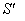 is called Special Lorentz transformation which can be written as [1]
is called Special Lorentz transformation which can be written as [1]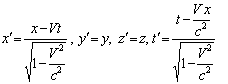
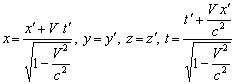
 of
of  with respect to
with respect to  is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 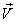 has three components Vx, Vy and Vz. Then the relation between the coordinates of
has three components Vx, Vy and Vz. Then the relation between the coordinates of 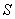 and
and 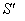 is called Most general Lorentz transformation which can be written as [2]
is called Most general Lorentz transformation which can be written as [2]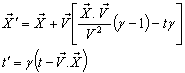
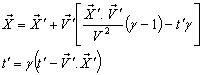
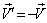 ,
,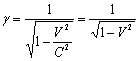 in unit of C
in unit of C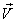 of S' with respect to
of S' with respect to  is not along X-axis; i.e., the velocity
is not along X-axis; i.e., the velocity 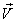 has three components, Vx, Vy, and Vz. Let in this case Z and Z' be the space parts in
has three components, Vx, Vy, and Vz. Let in this case Z and Z' be the space parts in 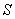 and S' frames, respectively. Then using the mixed product
and S' frames, respectively. Then using the mixed product 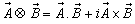 , Mixed number Lorentz transformations [3 – 6] can be written as
, Mixed number Lorentz transformations [3 – 6] can be written as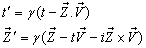
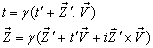
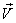 of S' with respect to
of S' with respect to  also has three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case
also has three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case  and
and 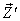 be the space parts in
be the space parts in 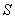 and S' frames respectively. Then using geometric product of two vectors
and S' frames respectively. Then using geometric product of two vectors 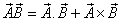 the geometric product Lorentz transformation [7, 8] can be written as
the geometric product Lorentz transformation [7, 8] can be written as 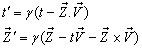
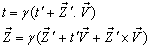
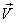 of S' with respect to
of S' with respect to  has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case
has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case  and
and 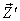 be the space parts in
be the space parts in 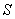 and S' frames respectively. Then using quaternion product
and S' frames respectively. Then using quaternion product 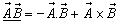 the Quaternion Lorentz transformation [9-12] can be written as
the Quaternion Lorentz transformation [9-12] can be written as 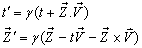
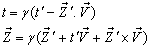
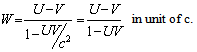
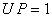 then
then 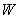 will be change to
will be change to 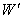 where
where 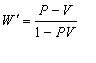 Reciprocal property demands that if
Reciprocal property demands that if 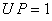 then
then  Now,
Now,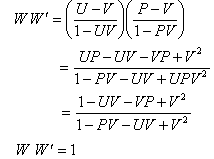
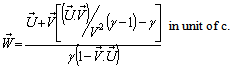
 by
by  where
where  then
then 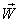 will be change to
will be change to 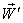 where
where 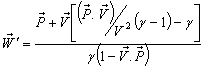 Reciprocal property demands that if
Reciprocal property demands that if 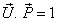 then
then 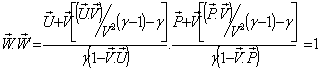 Now,
Now,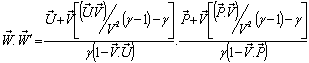 Can be written as
Can be written as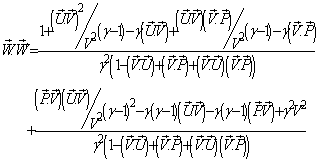 So,
So, 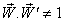
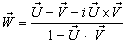
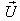 by
by 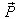 where
where 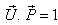 then
then 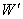 will be change to
will be change to 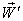 where
where 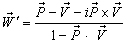 Reciprocal property demands that if
Reciprocal property demands that if 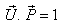 then
then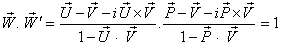 Now,
Now,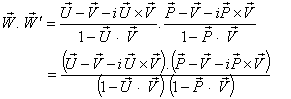 can be written as
can be written as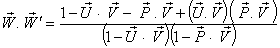
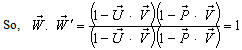
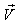 by
by 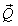 where
where 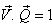 then
then 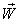 will be change to
will be change to 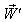 where
where 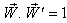 Consequently, Mixed number Lorentz transformation satisfies the reciprocal property.
Consequently, Mixed number Lorentz transformation satisfies the reciprocal property. 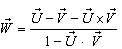
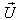 by
by 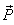 where
where 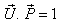 then
then 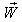 will be change to
will be change to 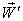 where
where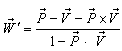 Reciprocal property demands that if
Reciprocal property demands that if 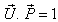 then
then 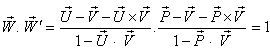 Now,
Now, 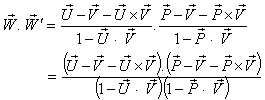 Can be written as
Can be written as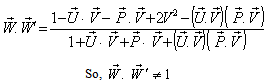
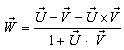
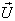 by
by 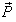 where
where 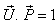 then
then 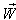 will be change to
will be change to 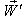 where
where 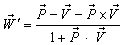 Reciprocal property demands that if
Reciprocal property demands that if 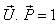 then
then 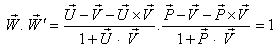 Now,
Now, 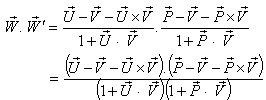 Can be written as
Can be written as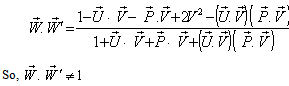
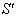 ,
,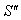 and
and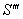 where the frame S is at rest and the frame
where the frame S is at rest and the frame 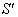 is moving with velocity
is moving with velocity 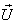 with respect to S,
with respect to S, 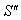 is moving with velocity
is moving with velocity 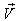 with respect to
with respect to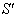 ,
, 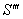 is moving with velocity
is moving with velocity 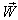 respect to
respect to 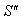 then associative property says that
then associative property says that 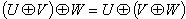 [Fig-1]. We are going to discuss the associative property of different Lorentz transformations in unit of c. Let
[Fig-1]. We are going to discuss the associative property of different Lorentz transformations in unit of c. Let 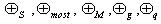 are the symbols of the Lorentz sum of Special, Most general, Mixed number, geometric product, and Quaternion product Lorentz transformations respectively.
are the symbols of the Lorentz sum of Special, Most general, Mixed number, geometric product, and Quaternion product Lorentz transformations respectively.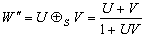
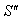 moves with velocity
moves with velocity 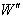 with respect to S , then according to the velocity addition formula for special Lorentz transformation [13] can be written as
with respect to S , then according to the velocity addition formula for special Lorentz transformation [13] can be written as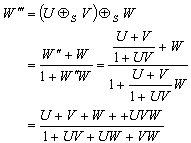
 moves with velocity V with respect to
moves with velocity V with respect to  and
and  moves with velocity W with respect to
moves with velocity W with respect to 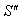 then according to the velocity addition formula for the Special Lorentz transformation [13] the resultant velocity of V and W can be written as
then according to the velocity addition formula for the Special Lorentz transformation [13] the resultant velocity of V and W can be written as 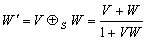
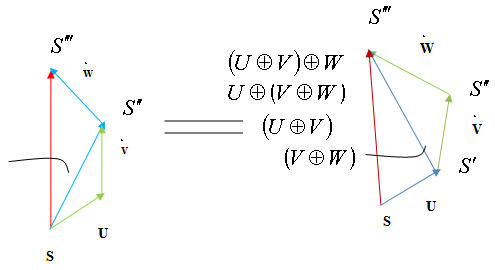
 moves with velocity U with respect to S and
moves with velocity U with respect to S and 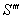 moves with velocity
moves with velocity 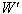 with respect to
with respect to 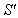 then the resultant velocity [13] of U and
then the resultant velocity [13] of U and 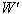 can be written as
can be written as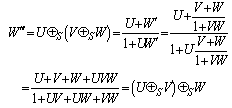
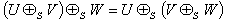
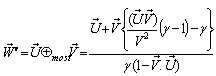
 moves with velocity
moves with velocity 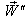 with respect to S and
with respect to S and 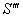 moves with velocity
moves with velocity 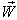 respect to
respect to 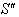 then according to the velocity addition formula for most general Lorentz transformation [14] can be written as
then according to the velocity addition formula for most general Lorentz transformation [14] can be written as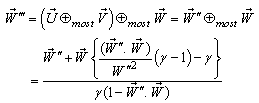 Substituting the value of
Substituting the value of 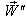 we have
we have
 moves with velocity
moves with velocity 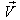 with respect to
with respect to 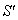 and
and 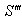 moves with velocity
moves with velocity 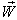 with respect to
with respect to 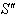 then according to the velocity addition formula for most general Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for most general Lorentz transformation [14] the resultant velocity of 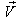 and
and 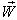 can be written as
can be written as 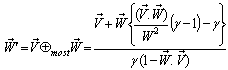
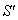 moves with velocity
moves with velocity 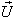 with respect to S and
with respect to S and 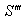 moves with velocity
moves with velocity 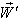 with respect to
with respect to 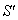 then the resultant velocity [14] of
then the resultant velocity [14] of 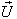 and
and 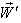 can be written as
can be written as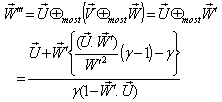
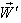 the above expression can be written as
the above expression can be written as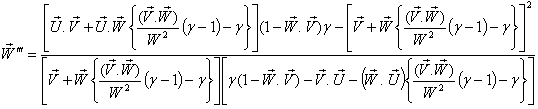
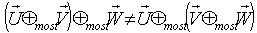
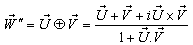
 moves with velocity
moves with velocity  with respect to S and
with respect to S and 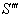 moves with velocity
moves with velocity 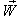 respect to
respect to 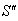 then according to the velocity addition formula for mixed number Lorentz transformation [14] can be written as
then according to the velocity addition formula for mixed number Lorentz transformation [14] can be written as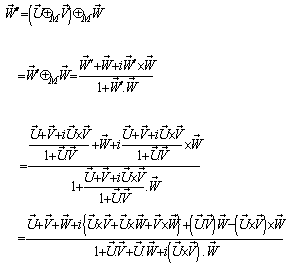
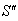 moves with velocity
moves with velocity 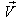 with respect to
with respect to 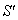 and
and 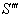 moves with velocity
moves with velocity 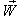 with respect to
with respect to 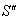 then according to the velocity addition formula for mixed number Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for mixed number Lorentz transformation [14] the resultant velocity of 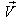 and
and 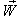 can be written as
can be written as 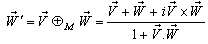
 moves with velocity
moves with velocity  with respect to S and
with respect to S and  moves with velocity
moves with velocity 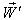 with respect to
with respect to 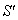 then using (34) the resultant velocity [14] of
then using (34) the resultant velocity [14] of 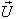 and
and 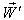 can be written as
can be written as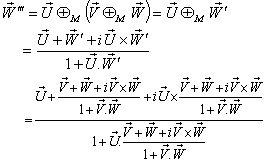
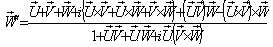 Hence,
Hence,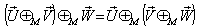
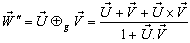
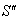 moves with velocity
moves with velocity 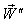 with respect to S and
with respect to S and 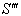 moves with velocity
moves with velocity 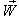 respect to
respect to 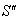 then according to the velocity addition formula for geometric product Lorentz transformation [14] can be written as
then according to the velocity addition formula for geometric product Lorentz transformation [14] can be written as
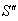 moves with velocity
moves with velocity 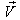 with respect to
with respect to 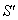 and
and 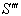 moves with velocity
moves with velocity 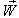 with respect to
with respect to 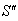 then according to the velocity addition formula for the Geometric product Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for the Geometric product Lorentz transformation [14] the resultant velocity of 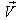 and
and 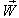 can be written as
can be written as 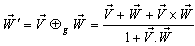
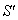 moves with velocity
moves with velocity 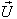 with respect to S and
with respect to S and 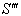 moves with velocity
moves with velocity 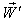 with respect to
with respect to 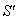 then using (39) the resultant velocity [14] of
then using (39) the resultant velocity [14] of 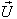 and
and 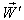 can be written as
can be written as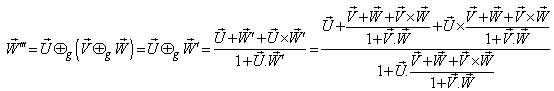 can be written as
can be written as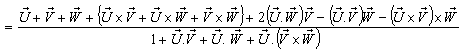
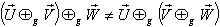
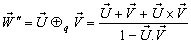
 moves with velocity
moves with velocity  with respect to S and
with respect to S and  moves with velocity
moves with velocity 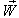 respect to
respect to 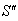 then according to the velocity addition formula for the Quaternion Lorentz transformation [14] can be written as
then according to the velocity addition formula for the Quaternion Lorentz transformation [14] can be written as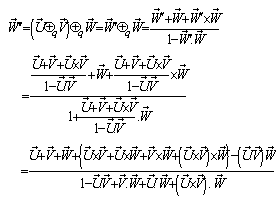
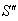 moves with velocity
moves with velocity 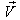 with respect to
with respect to 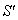 and
and 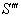 moves with velocity
moves with velocity 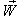 with respect to
with respect to 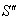 then according to the velocity addition formula for the Quaternion Lorentz transformation [14] the resultant velocity of
then according to the velocity addition formula for the Quaternion Lorentz transformation [14] the resultant velocity of 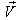 and
and 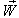 can be written as
can be written as 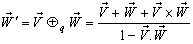
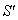 moves with velocity
moves with velocity 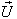 with respect to S and
with respect to S and 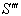 moves with velocity
moves with velocity 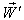 with respect to
with respect to 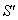 then using (44) the resultant velocity [14] of
then using (44) the resultant velocity [14] of 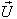 and
and 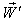 can be written as
can be written as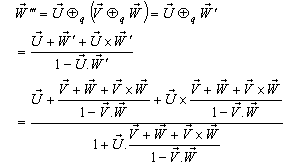
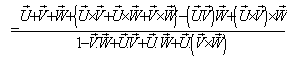 Hence,
Hence,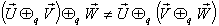
 ,
,  and
and 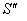 where
where 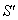 moves with velocity
moves with velocity 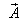 with respect to
with respect to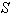 and
and 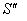 moves with velocity
moves with velocity 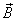 with respect to
with respect to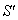 . If
. If 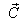 be the velocity of
be the velocity of 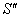 with respect to
with respect to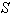 .
.
 , then according to Lorentz sum we can write
, then according to Lorentz sum we can write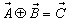
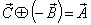
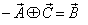
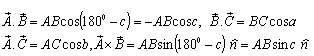 Now the isotropic property demands that if
Now the isotropic property demands that if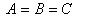 then
then 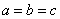
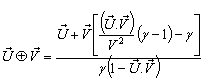
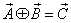
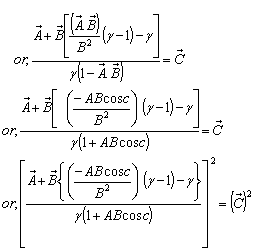
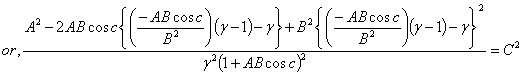
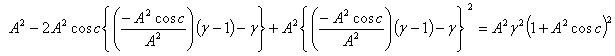
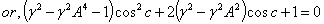
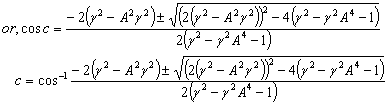
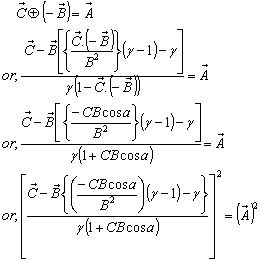
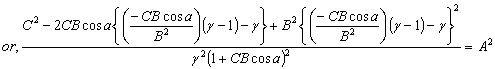
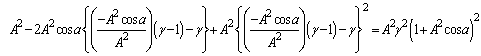
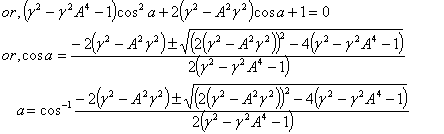
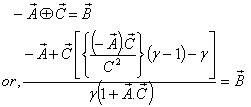
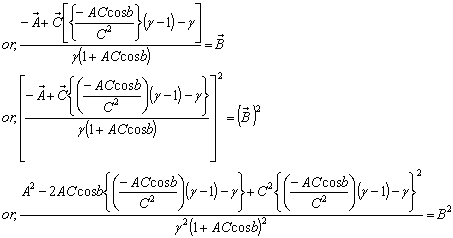
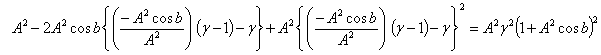
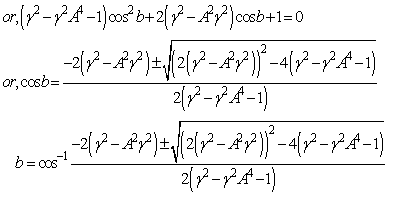
 Hence, most general Lorentz transformation satisfies the isotropic property
Hence, most general Lorentz transformation satisfies the isotropic property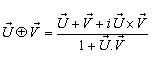
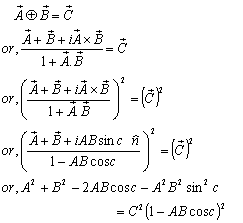
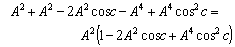
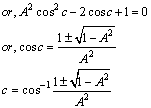
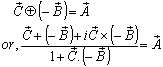
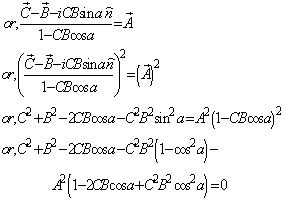
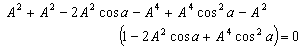
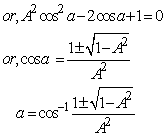
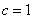 )
)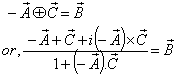
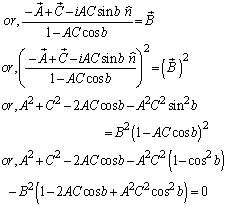
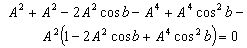
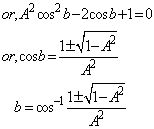
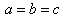 Hence, Mixed number Lorentz transformation satisfies the isotropic property.
Hence, Mixed number Lorentz transformation satisfies the isotropic property.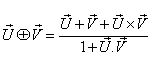
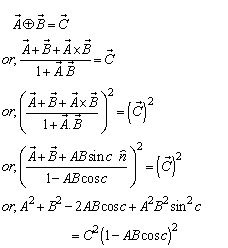
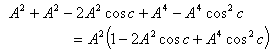
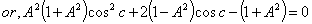
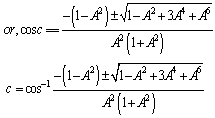
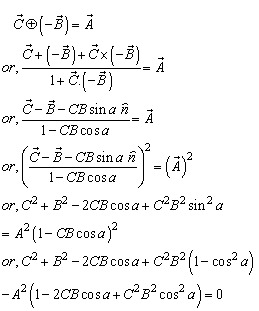
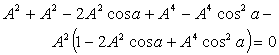
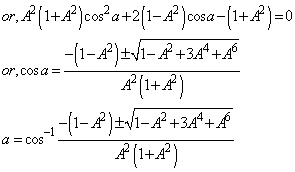
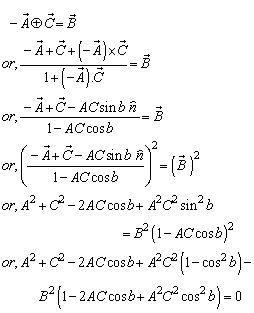
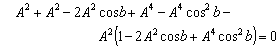
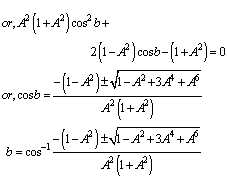
 Hence, geometric product Lorentz Transformation satisfies the isotropic property
Hence, geometric product Lorentz Transformation satisfies the isotropic property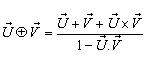
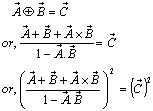
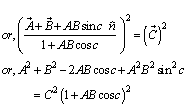
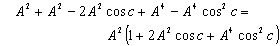
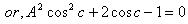
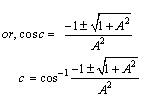
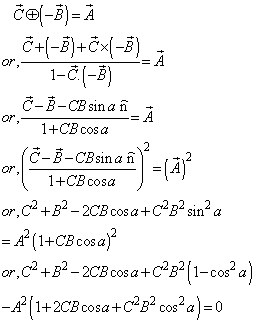
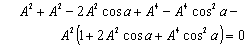
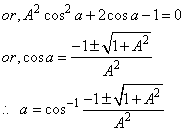
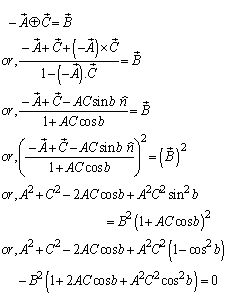
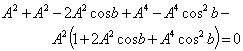
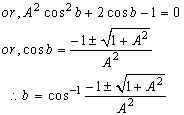
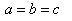 Hence, Quaternion Lorentz transformation satisfies the isotropic property.
Hence, Quaternion Lorentz transformation satisfies the isotropic property. ,
, 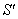 and
and 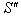 where
where 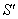 has relative velocity
has relative velocity 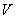 with respect to
with respect to 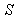 along positive x-axis and
along positive x-axis and 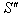 has relative velocity
has relative velocity 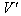 with respect to
with respect to 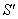 along the same direction as shown in fig.1. According to special Lorentz transformation we get
along the same direction as shown in fig.1. According to special Lorentz transformation we get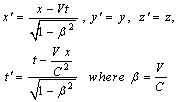

 and
and  coincide at
coincide at  the space and time co-ordinates in
the space and time co-ordinates in 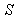 and
and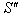 related as
related as 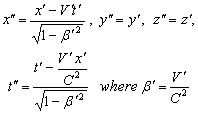
 be the resultant velocity of
be the resultant velocity of 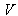 and
and 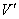 then from the velocity addition formula [14] we get
then from the velocity addition formula [14] we get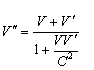
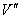 is the velocity of system
is the velocity of system 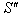 relative to
relative to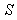 . To prove this result we have to show that
. To prove this result we have to show that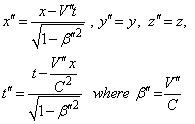
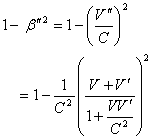 Can be written as
Can be written as
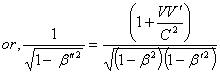
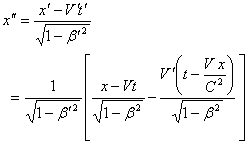 Can be written as
Can be written as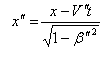 So,
So, 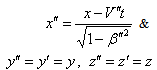
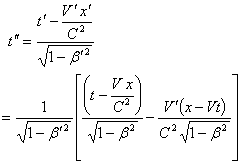 Can be written as
Can be written as 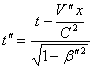 Thus the result of two Lorentz transformations is itself a Lorentz transformation. Hence Special Lorentz transformations form a group.
Thus the result of two Lorentz transformations is itself a Lorentz transformation. Hence Special Lorentz transformations form a group.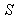 ,
, 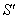 and
and 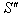 where
where 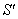 moves with velocity
moves with velocity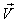 with respect to
with respect to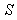 and
and 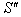 moves with velocity
moves with velocity 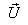 with respect to
with respect to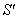 . If
. If 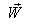 be the velocity of
be the velocity of 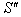 with respect to
with respect to 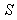

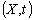 in
in 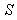 and
and 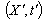 in
in 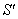 can be expressed by most general Lorentz transformation by
can be expressed by most general Lorentz transformation by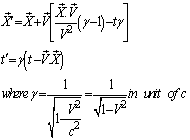
 in
in  and
and 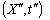 in
in 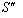 can be expressed by most general Lorentz transformation by
can be expressed by most general Lorentz transformation by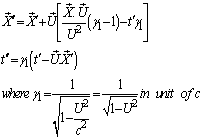
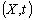 in
in 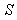 and
and 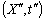 in
in 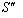 can be expressed by most general Lorentz transformation by
can be expressed by most general Lorentz transformation by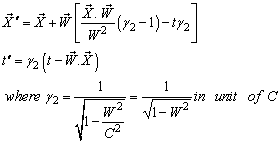
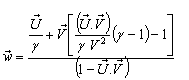 Now we have from (85)
Now we have from (85)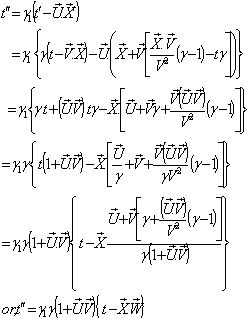 Where
Where 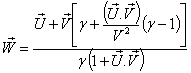 Now we have to show
Now we have to show 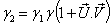 We know
We know 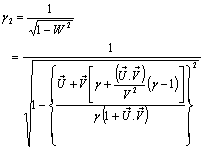 Can be written as
Can be written as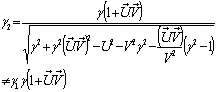 Hence, the time part of the Most General Lorentz transformation does not satisfy the group property.Again from equation (85)
Hence, the time part of the Most General Lorentz transformation does not satisfy the group property.Again from equation (85)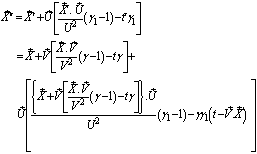 Which can be written as
Which can be written as 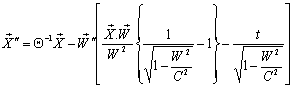 Where the operator
Where the operator 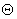 in general is different from the unit operator.
in general is different from the unit operator. 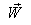 is the velocity of the system
is the velocity of the system 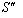 relative to
relative to 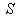 and
and 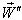 is the velocity of the system
is the velocity of the system 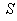 relative to
relative to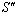 .We get
.We get 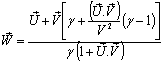 and
and 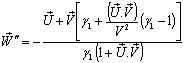 Now
Now 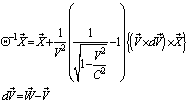
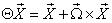
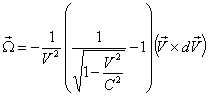 UThe rotation operator thus represents an infinitesimal rotation around the direction of the vector
UThe rotation operator thus represents an infinitesimal rotation around the direction of the vector 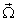 [3]Hence, most general Lorentz transformation does not satisfy the group property without rotation
[3]Hence, most general Lorentz transformation does not satisfy the group property without rotation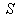 ,
, 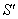 and
and 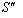 where
where 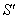 moves with velocity
moves with velocity 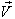 with respect to
with respect to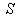 and
and 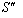 moves with velocity
moves with velocity 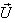 with respect to
with respect to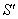 .If
.If 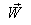 be the velocity of
be the velocity of 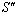 with respect to
with respect to 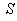 then the relation between the co-ordinates
then the relation between the co-ordinates 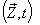 in
in 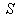 and
and 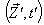 in
in 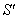 can be expressed by mixed number Lorentz transformation by
can be expressed by mixed number Lorentz transformation by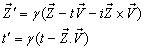
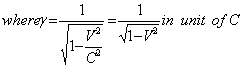 Similarly, the relation between the co-ordinates
Similarly, the relation between the co-ordinates 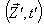 in
in 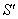 and
and 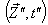 in
in 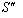 can be expressed by Mixed Number Lorentz transformation by
can be expressed by Mixed Number Lorentz transformation by 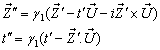
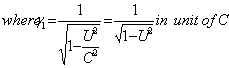 Similarly, the relation between the co-ordinates
Similarly, the relation between the co-ordinates  in
in  and
and  in
in 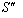 can be expressed by mixed Number Lorentz transformation by
can be expressed by mixed Number Lorentz transformation by 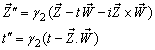
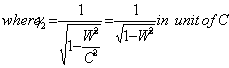 The velocity addition formula for mixed Number Lorentz transformation [14] can be written as
The velocity addition formula for mixed Number Lorentz transformation [14] can be written as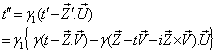
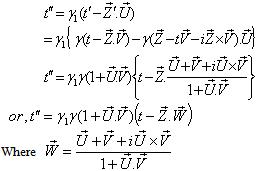
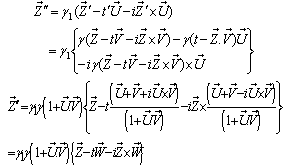 Where
Where 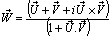 Now we have to show that
Now we have to show that 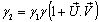
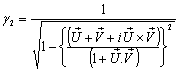
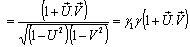 Hence,
Hence, 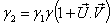 Therefore, mixed Number Lorentz transformation satisfies the group property
Therefore, mixed Number Lorentz transformation satisfies the group property ,
, 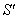 and
and 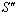 where
where 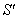 moves with velocity
moves with velocity 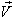 with respect to
with respect to and
and 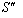 moves with velocity
moves with velocity 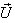 with respect to
with respect to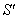 .If
.If 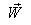 be the velocity of
be the velocity of 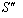 with respect to
with respect to 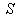 then the relation between the co-ordinates
then the relation between the co-ordinates 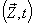 in
in 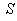 and
and 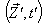 in
in 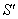 can be expressed by geometric product Lorentz transformation by
can be expressed by geometric product Lorentz transformation by 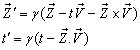
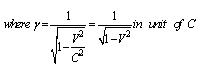 Similarly, the relation between the co-ordinates
Similarly, the relation between the co-ordinates 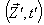 in
in 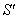 and
and 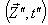 in
in 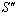 can be expressed by geometric product Lorentz transformation by
can be expressed by geometric product Lorentz transformation by 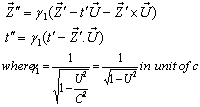
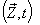 in
in 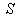 and
and 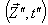 in
in 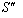 can be expressed by geometric Product Lorentz transformation by
can be expressed by geometric Product Lorentz transformation by 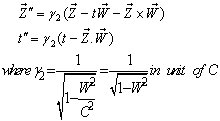
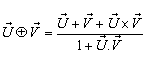
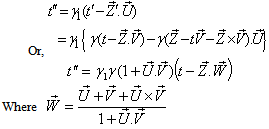 Again from equation (94) we can write
Again from equation (94) we can write 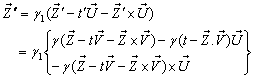
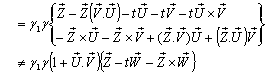 Where
Where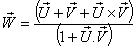 Now we have to show that
Now we have to show that 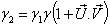
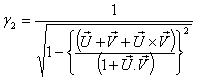
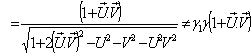 Therefore, Geometric Product Lorentz transformation does not satisfy the isotropic property
Therefore, Geometric Product Lorentz transformation does not satisfy the isotropic property ,
,  and
and  where
where 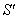 moves with velocity
moves with velocity 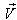 with respect to
with respect to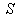 and
and 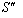 moves with velocity
moves with velocity 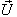 with respect to
with respect to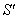 .If
.If 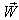 be the velocity of
be the velocity of 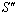 with respect to
with respect to 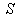 then the relation between the co-ordinates
then the relation between the co-ordinates 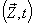 in
in 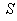 and
and 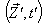 in
in 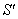 can be expressed by Quaternion Product Lorentz transformation by
can be expressed by Quaternion Product Lorentz transformation by 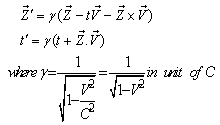
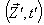 in
in 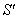 and
and 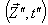 in
in 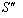 can be expressed by Quaternion Product Lorentz transformation by
can be expressed by Quaternion Product Lorentz transformation by 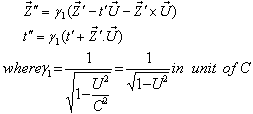
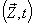 in
in 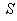 and
and 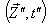 in
in 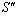 can be expressed by Quaternion Product Lorentz transformation by
can be expressed by Quaternion Product Lorentz transformation by 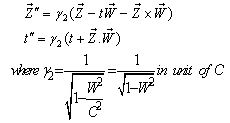
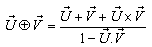
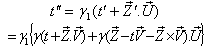 Or,
Or, 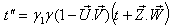 Where
Where 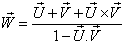 Again from equation (98) we can write
Again from equation (98) we can write 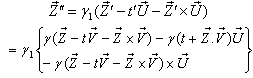 Can be written as
Can be written as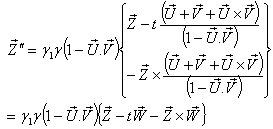 Where
Where 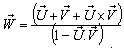 Now we have to show that
Now we have to show that 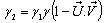
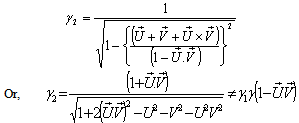 Therefore, Quaternion Product Lorentz transformation does not satisfy the group property
Therefore, Quaternion Product Lorentz transformation does not satisfy the group property Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML