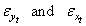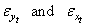P. M. Kgosi, K. Thaga, D. K. Shangodoyin
University of Botswana, Botswana
Correspondence to: D. K. Shangodoyin, University of Botswana, Botswana.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The model structure and cross and cross correlation functions of observed time series variables with their respective residuals are examined for the causal relationship in the presence of autocorrelated residuals. A two-stage procedure that adjusts for residuals autocorrelation and produces robust dynamic model is proposed. The new model is illustrated with real life data.
Keywords:
Causal Relationship, Autocorrelation, Dynamic Models, Residuals And Time Domain Models
Cite this paper: P. M. Kgosi, K. Thaga, D. K. Shangodoyin, Specification of Dynamic Distributed Lag Model in the Presence of Autocorrelated Residuals, American Journal of Mathematics and Statistics, Vol. 3 No. 3, 2013, pp. 99-104. doi: 10.5923/j.ajms.20130303.02.
1. Introduction
Dynamic distributed lag models are used in time series literature to investigate causal relationship between input (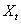 ) and output (
) and output (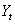 ) series. The dynamic models have been found very useful in economic (Gomez, 2009), biological (Harvey, 1989) and process control (Box and Jenkins, 1976) and model relates to control an endogenous variable Y to an exogenous variable X with an independent noise term.The primary aim of statistical inference is to narrow the scope of statistical model in the light of observed values of the exogenous and endogenous variables. Certain structures which seemed plausible a priori may not appear to conform to the norms and assumptions of the statistical models specified for use and this may hinder inferences on the results obtained. This situation is of practical importance to analysts and does motivate the present study (see Malinvaud, 1966 and Koutsoyiannis, 1977).In modeling economic and engineering systems, a problem often arises as to how two time series are related (Shangodoyin, 1994 and 2000) and if the two time series can be transformed in such a way that they are jointly covariance stationary; then interrelationships can often be usefully described by either cross-correlation function or cross spectrum. Bartlett (1946) presents the asymptotic covariance between two cross correlation estimates under the assumption that the two series X and Y are jointly covariance and normally distributed. This relation (Box and Jenkins 1976) indicates that the covariance patterns of the cross-correlations can be quite complicated depending on
) series. The dynamic models have been found very useful in economic (Gomez, 2009), biological (Harvey, 1989) and process control (Box and Jenkins, 1976) and model relates to control an endogenous variable Y to an exogenous variable X with an independent noise term.The primary aim of statistical inference is to narrow the scope of statistical model in the light of observed values of the exogenous and endogenous variables. Certain structures which seemed plausible a priori may not appear to conform to the norms and assumptions of the statistical models specified for use and this may hinder inferences on the results obtained. This situation is of practical importance to analysts and does motivate the present study (see Malinvaud, 1966 and Koutsoyiannis, 1977).In modeling economic and engineering systems, a problem often arises as to how two time series are related (Shangodoyin, 1994 and 2000) and if the two time series can be transformed in such a way that they are jointly covariance stationary; then interrelationships can often be usefully described by either cross-correlation function or cross spectrum. Bartlett (1946) presents the asymptotic covariance between two cross correlation estimates under the assumption that the two series X and Y are jointly covariance and normally distributed. This relation (Box and Jenkins 1976) indicates that the covariance patterns of the cross-correlations can be quite complicated depending on 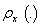 and
and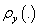 , although it is known that a set of cross-correlation estimates
, although it is known that a set of cross-correlation estimates 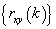 at a fixed number of chosen lag k are consistent estimates for
at a fixed number of chosen lag k are consistent estimates for  and are asymptotically normally distributed under suitable assumptions on X and Y (Hannah; 1970). When the series are indeed independent, the normality assumption is no longer required (Haugh and Box, 1977) but analyst may still be misled in the interpretation of the cross-correlation estimates by attributing some significance to the apparent patterns in the cross-correlation function, which infact are as a result of sampling properties of the estimates used (Box and newbold 1971). Alternatively if the series X and Y are each white noise, then the Bartlet (1946) expression of covariance between two cross-correlation estimates becomes simplified and it will be quite easy to interpret the cross-correlation estimates only in the situation of the independent white noise series. Fortunately, this latter situation is of practical importance because at the identification stage of the model building process, one is often interested in comparing these cross-correlation estimates with bench marks appropriate to the null hypothesis of series independence and more importantly to know when cutoff takes place.To decide whether
and are asymptotically normally distributed under suitable assumptions on X and Y (Hannah; 1970). When the series are indeed independent, the normality assumption is no longer required (Haugh and Box, 1977) but analyst may still be misled in the interpretation of the cross-correlation estimates by attributing some significance to the apparent patterns in the cross-correlation function, which infact are as a result of sampling properties of the estimates used (Box and newbold 1971). Alternatively if the series X and Y are each white noise, then the Bartlet (1946) expression of covariance between two cross-correlation estimates becomes simplified and it will be quite easy to interpret the cross-correlation estimates only in the situation of the independent white noise series. Fortunately, this latter situation is of practical importance because at the identification stage of the model building process, one is often interested in comparing these cross-correlation estimates with bench marks appropriate to the null hypothesis of series independence and more importantly to know when cutoff takes place.To decide whether 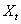 series and the historical values of
series and the historical values of 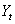 cause
cause 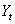 it is appealing to consider whether or not the residuals
it is appealing to consider whether or not the residuals 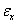 and
and 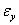 are related. Haugh and Box (1977) relates
are related. Haugh and Box (1977) relates 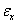 and
and 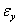 under the assumption that X and Y are independent; the autocorrelation function of the white noise series
under the assumption that X and Y are independent; the autocorrelation function of the white noise series 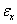 and
and 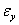 are particularly simple and the specification of the model connecting these series depends on the appearance of the cross-correlation function for the bivariate process which may be individually autocorrelated.In general linear process the random terms of different observations are assumed to be independent, this means that all the covariances of any
are particularly simple and the specification of the model connecting these series depends on the appearance of the cross-correlation function for the bivariate process which may be individually autocorrelated.In general linear process the random terms of different observations are assumed to be independent, this means that all the covariances of any 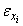 with any other
with any other 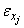 should be zero. But situation arises when the value which the random term
should be zero. But situation arises when the value which the random term 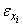 assumed depends on the value which
assumed depends on the value which 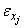 assumed, this is pure violation of the assumptions underlying general linear process (See Walter 2010).This study specifically aims at providing covariance structures that links
assumed, this is pure violation of the assumptions underlying general linear process (See Walter 2010).This study specifically aims at providing covariance structures that links 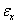 and
and 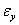 to express the real relationship that exists between endogenous and exogenous variables in the presence of autocorrelated residuals or disturbance terms. We shall specifically consider two stage procedure, such that at the first stage the residual series for each of the observed series X and Y are generated using admissible time domain model adjusted for autocorrelations in their residuals, while at the second stage when no significant cross-correlation occurs at non-negative lags between
to express the real relationship that exists between endogenous and exogenous variables in the presence of autocorrelated residuals or disturbance terms. We shall specifically consider two stage procedure, such that at the first stage the residual series for each of the observed series X and Y are generated using admissible time domain model adjusted for autocorrelations in their residuals, while at the second stage when no significant cross-correlation occurs at non-negative lags between 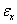 and
and 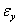 a complete model for X and Y as specified and the level of causality is then identified.
a complete model for X and Y as specified and the level of causality is then identified.
2. Specification of the Model Adjusted for Autocorrelated Residual
A two stage procedure is considered on the dynamic distributed lag model building. At the first stage we fitted an admissible time domain process to each series X and Y using Box and Jenkins (1976) approach and testing for serial autocorrelation in residuals. The second stage of the model building involves adjusting the residuals series and for autocorrelation. The adjusted residual series 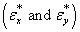 are then cross-correlated in the usual way and a tentative dynamic shock model is identified which relates
are then cross-correlated in the usual way and a tentative dynamic shock model is identified which relates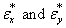 . By combining the univariate model for series
. By combining the univariate model for series 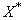 and
and 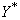 with the identified model connecting
with the identified model connecting 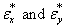 , we then identify a distributed lag model relating
, we then identify a distributed lag model relating 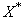 and
and 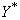 .
.
2.1. Model Specification
Suppose that the univariate forecasting model of Y be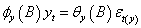 | (1) |
Where 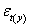 is the residual term,
is the residual term, 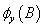 = 1-
= 1- 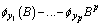 and
and 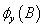 =
= 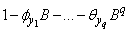 ; similarly we write the residual series
; similarly we write the residual series 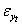 driving X as
driving X as 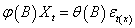 | (2) |
In practice the residuals taken are taken as a sequence of uncorrelated random variables from a fixed distribution with constant mean 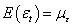 (usually assumed to be zero), a finite constant variance
(usually assumed to be zero), a finite constant variance 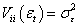 and covariance
and covariance 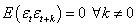 .At the first stage, assuming X and Y are individually and jointly covariance stationary series, it is possible to model each series individually as:
.At the first stage, assuming X and Y are individually and jointly covariance stationary series, it is possible to model each series individually as: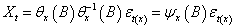 | (3) |
and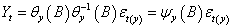 | (4) |
The residual series for 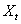 is
is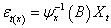 | (5) |
Where, 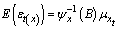 ,
,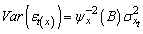 and for autocorrelation we have
and for autocorrelation we have 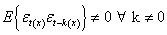 . Similarly, the residual series for
. Similarly, the residual series for 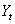 is
is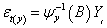 | (6) |
Also, 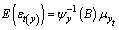
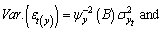
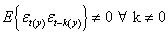 To test for dependence in the disturbance terms we use the asymptotic or large sample test statistic, this states that under null hypothesis of no serial correlation it can be shown that having fitted the model
To test for dependence in the disturbance terms we use the asymptotic or large sample test statistic, this states that under null hypothesis of no serial correlation it can be shown that having fitted the model 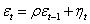 | (7) |
Where 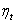 is normally distributed with zero mean and constant variance; then
is normally distributed with zero mean and constant variance; then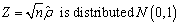 . If the absolute value of Z exceeds the critical value at the chosen level of significance, we reject the null hypothesis.At the second stage, the disturbances
. If the absolute value of Z exceeds the critical value at the chosen level of significance, we reject the null hypothesis.At the second stage, the disturbances 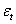 are unobservable and the nature of serial correlation is often a matter of speculation or practical exigencies. In practice, it is usually assumed that the
are unobservable and the nature of serial correlation is often a matter of speculation or practical exigencies. In practice, it is usually assumed that the 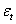 follows the first- order autoregressive process defined as
follows the first- order autoregressive process defined as 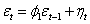 | (8) |
Where 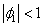 and the
and the 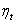 follows the ordinary least squares assumptions of zero expected value; constant variance and none autocorrelation.Assuming the validity of equation (8), the serial correlation problem can be resolved if
follows the ordinary least squares assumptions of zero expected value; constant variance and none autocorrelation.Assuming the validity of equation (8), the serial correlation problem can be resolved if 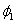 is known or estimated. To see this, assume the model structure defined in equation (3), that is
is known or estimated. To see this, assume the model structure defined in equation (3), that is 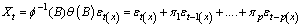 | (9) |
If equation (9) holds for all 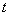 , then it is true for
, then it is true for 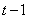 , and
, and 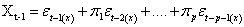 | (10) |
By multiplying equation (10) by 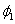 and subtracting the result from (9) gives
and subtracting the result from (9) gives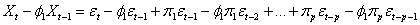 | (11) |
If we write equation (11) using backward shift operation, it reduces to:Thus further simplified as: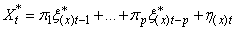 | (12) |
Where 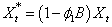 and
and 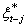
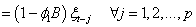 Since
Since 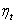 satisfy all the assumptions of general linear model, one can proceed to apply OLS to the adjusted series
satisfy all the assumptions of general linear model, one can proceed to apply OLS to the adjusted series 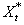 and
and 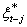 to give estimators of the dynamic model parameters, these estimators will all have optimum properties of BLUE. We can express equation (12) for the output series as
to give estimators of the dynamic model parameters, these estimators will all have optimum properties of BLUE. We can express equation (12) for the output series as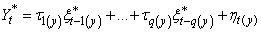 | (13) |
And assuming that the series 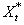 and
and 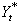 given in equations (12) and (13) are jointly covariance stationary series; then we have
given in equations (12) and (13) are jointly covariance stationary series; then we have 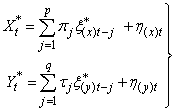 | (14) |
Since the residual series of the specification 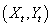 are independent, the covariance structure of
are independent, the covariance structure of 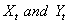 defined in equations (3) and (4) may be written as:
defined in equations (3) and (4) may be written as: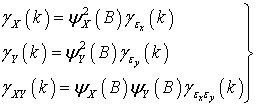 | (15) |
According to Haugh and Box (1977), the joint process 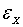 and
and 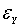 is not bivariate white noise, because the
is not bivariate white noise, because the 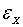 and
and 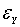 may be correlated as non-zero lags, that
may be correlated as non-zero lags, that 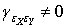 exist
exist 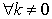 since this may arise, one could suspect autocorrelation in residuals. Equation (14) could provide the covariance structure of
since this may arise, one could suspect autocorrelation in residuals. Equation (14) could provide the covariance structure of  in terms of uncorrelated residuals
in terms of uncorrelated residuals , the covariances are derived as follows:
, the covariances are derived as follows: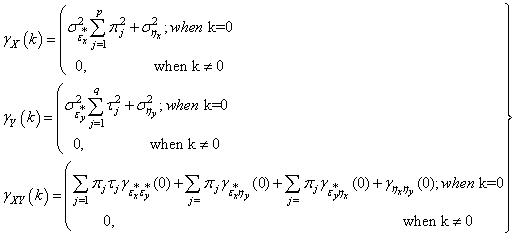 | (16) |
The covariance structures shown in equation (16) have residual series which are non-autocorrelated and could then be used to write the final dynamic model with non-autocorrelated errors. Based on the methodology discussed by Haugh and Box (1977) and Shangodoyin (2000), we derive the dynamic distributed lag model connecting two series with autocorrelated residuals as: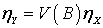 | (17) |
Where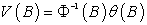 . The model described in equation (17) is a modified version of what was given by Box and Jenkins (1976, page 380). By using the structural form on equation (14) in (17) we have:
. The model described in equation (17) is a modified version of what was given by Box and Jenkins (1976, page 380). By using the structural form on equation (14) in (17) we have: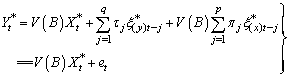 | (18) |
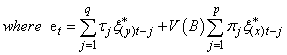 Equation (18) gives a measure of causal effect of X-input series on Y-output series. Similarly, a measure of causal effect of
Equation (18) gives a measure of causal effect of X-input series on Y-output series. Similarly, a measure of causal effect of 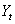 on
on 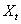 could be obtained as: Let the fitted model between
could be obtained as: Let the fitted model between 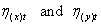 be
be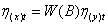 , then the causality measure is
, then the causality measure is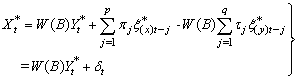 | (19) |
Where 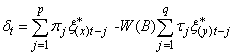 . The latter parts of equations (18) and (19) would be compared with the conventional dynamic distributed lag model:
. The latter parts of equations (18) and (19) would be compared with the conventional dynamic distributed lag model: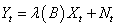 | (20) |
The comparison will on the premise that both 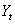 and
and 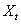 are related with autocorrelated residuals in the form described in equations (3) and (4) and that
are related with autocorrelated residuals in the form described in equations (3) and (4) and that 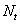 is assumed to be autocorrelated residuals which are linearly independent of input series
is assumed to be autocorrelated residuals which are linearly independent of input series 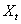 described in equation (20).
described in equation (20).
3. Empirical Illustration
The data utilized in this study is from Box and Jenkins (1976) series M, this is data on sales (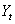 ) and leading indicator (
) and leading indicator (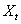 ) collected over 150 time points. The series are individually verified for unit root using Augmented Dickey Fuller (ADF) test statistic. In table 1 (see appendix), the null hypothesis of the presence of unit root is not rejected for both series as indicated by the value of ADF test statistic. These series are the differenced once; the values of ADF test statistic displayed in table 2 indicate that both series are stationary. We observe using the correlogram plot (see figures 1 and 2 in appendix) that autoregressive model of order one is appropriate for the difference series. The models fitted are:
) collected over 150 time points. The series are individually verified for unit root using Augmented Dickey Fuller (ADF) test statistic. In table 1 (see appendix), the null hypothesis of the presence of unit root is not rejected for both series as indicated by the value of ADF test statistic. These series are the differenced once; the values of ADF test statistic displayed in table 2 indicate that both series are stationary. We observe using the correlogram plot (see figures 1 and 2 in appendix) that autoregressive model of order one is appropriate for the difference series. The models fitted are: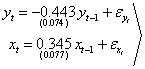 | (21) |
Residuals 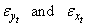 in equation (21) are verified for serial correlation using the large sample test statistic described in section 2 above. In table 2, we confirm that these residuals are individually stationary, serially correlated and normally distributed. Hence we transformed both the sales and leading indicator series using
in equation (21) are verified for serial correlation using the large sample test statistic described in section 2 above. In table 2, we confirm that these residuals are individually stationary, serially correlated and normally distributed. Hence we transformed both the sales and leading indicator series using 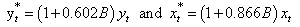 respectively. The autoregressive models of order one fitted to the transformed series are:
respectively. The autoregressive models of order one fitted to the transformed series are: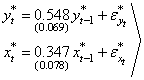 | (22) |
In table 3, we confirm that both  defined in equation (22) are individually stationary, serially non-correlated and normally distributed as indicated by the values of ADF, Z and Jarque-Bera (JB) statistics. The dynamic model between
defined in equation (22) are individually stationary, serially non-correlated and normally distributed as indicated by the values of ADF, Z and Jarque-Bera (JB) statistics. The dynamic model between  without adjusting for the effect of serial correlation in their errors is obtained thus:
without adjusting for the effect of serial correlation in their errors is obtained thus: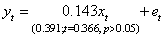 | (23) |
Table 1. Stationary Tests On Original And Differenced Data
 |
| |
|
Table 2. ADF and Z-Statistics results for
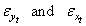
 |
| |
|
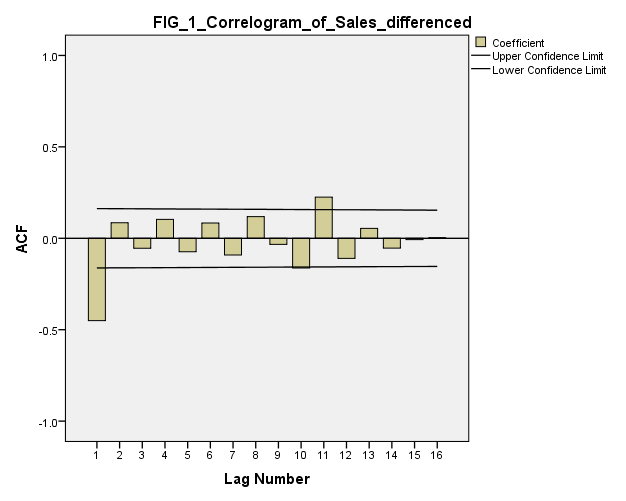 | Figure 1. Correlogram of Sales differenced |
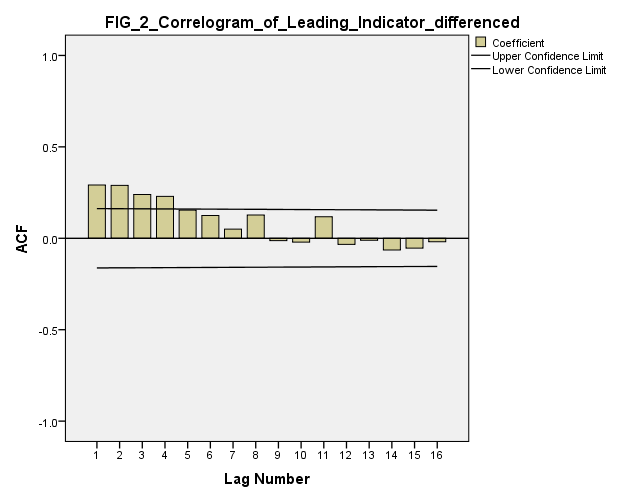 | Figure 2. Correlogram of Leading Indicator differenced |
Table 3. ADF and Z-Statistics results for
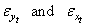
 |
| |
|
When the effect of serial correlation in residuals has been adjusted using the methodology described in section 2, the dynamic model fitted between 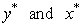 is:
is: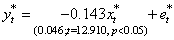 | (24) |
We observe that causality measured using dynamic equation free of residuals serial correlation is more reliable when the parameters of the models are significantly different from zero. From equations (23) and (24) the effect of serial correlation in residuals could be seen on the coefficient of the leading indicator series.
4. Conclusions
We have analytically and empirically confirm that a check on the serial correlation of residuals will produce a better fit for the dynamic structure between input and output series. In order to have meaningful dynamic model representing input-output series it is worthwhile to verify that all assumptions of general linear model are satisfied. More importantly if the residuals are correlated, the resultant dynamic model is spurious.
References
| [1] | Bartlett, M. S (1946): On the theoretical specification and sampling properties of autocorrelation time series. Journal of royal statistical society, Supplementary, 8, 27-41 |
| [2] | Box, G.E.P and Jenkins, G.M (1976): Time series analysis. Forecasting and Control. New Jersey: Prentice Hall. |
| [3] | Box, G.E.P and Newbold, P (1971): Some comments on a paper of Coer, Gomme and Kendall. Journal of royal statistical society, A(134,2) pp 229-240 |
| [4] | Gomez, V (2009): Transfer function model Identification. Boletin de Estadistica e Investigacion Operativa. Vol. 25, No.2, pp 109-115. |
| [5] | Hannah, E. J (1970): Multiple time series. Wiley publication, New York. |
| [6] | Haugh, L. D and Box, G.E.P (1977): Identification of dynamic regression models connecting two time series. Journal of American Statistical Association. Vol. 72, pp 121-130. |
| [7] | Koutsoyiannis, A (1977): Theory of Econometircs : An introductory exposition of econometric methods. Macmillian publishers. |
| [8] | Alinvaud, E (1966) : Statistical methods of econometrics. North-Hollad publishing company. |
| [9] | Shangodoyin, D. K (2000): Specification of dynamic distributed lag model connecting two outlier infested time series. Journal of science research , Vol.6(2),pp 97-103 |
| [10] | Shangodoyin, D.K (1994): On the specification of time series models in the presence of aberrant observations. Unpublished PhD Thesis. University of Ibadan, Ibadan, Nigeria. |
| [11] | Walter E (2010): Applied Econometric Time Series. John Wiley and Sons, Inc. |

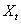 ) and output (
) and output (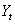 ) series. The dynamic models have been found very useful in economic (Gomez, 2009), biological (Harvey, 1989) and process control (Box and Jenkins, 1976) and model relates to control an endogenous variable Y to an exogenous variable X with an independent noise term.The primary aim of statistical inference is to narrow the scope of statistical model in the light of observed values of the exogenous and endogenous variables. Certain structures which seemed plausible a priori may not appear to conform to the norms and assumptions of the statistical models specified for use and this may hinder inferences on the results obtained. This situation is of practical importance to analysts and does motivate the present study (see Malinvaud, 1966 and Koutsoyiannis, 1977).In modeling economic and engineering systems, a problem often arises as to how two time series are related (Shangodoyin, 1994 and 2000) and if the two time series can be transformed in such a way that they are jointly covariance stationary; then interrelationships can often be usefully described by either cross-correlation function or cross spectrum. Bartlett (1946) presents the asymptotic covariance between two cross correlation estimates under the assumption that the two series X and Y are jointly covariance and normally distributed. This relation (Box and Jenkins 1976) indicates that the covariance patterns of the cross-correlations can be quite complicated depending on
) series. The dynamic models have been found very useful in economic (Gomez, 2009), biological (Harvey, 1989) and process control (Box and Jenkins, 1976) and model relates to control an endogenous variable Y to an exogenous variable X with an independent noise term.The primary aim of statistical inference is to narrow the scope of statistical model in the light of observed values of the exogenous and endogenous variables. Certain structures which seemed plausible a priori may not appear to conform to the norms and assumptions of the statistical models specified for use and this may hinder inferences on the results obtained. This situation is of practical importance to analysts and does motivate the present study (see Malinvaud, 1966 and Koutsoyiannis, 1977).In modeling economic and engineering systems, a problem often arises as to how two time series are related (Shangodoyin, 1994 and 2000) and if the two time series can be transformed in such a way that they are jointly covariance stationary; then interrelationships can often be usefully described by either cross-correlation function or cross spectrum. Bartlett (1946) presents the asymptotic covariance between two cross correlation estimates under the assumption that the two series X and Y are jointly covariance and normally distributed. This relation (Box and Jenkins 1976) indicates that the covariance patterns of the cross-correlations can be quite complicated depending on 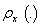 and
and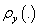 , although it is known that a set of cross-correlation estimates
, although it is known that a set of cross-correlation estimates 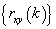 at a fixed number of chosen lag k are consistent estimates for
at a fixed number of chosen lag k are consistent estimates for  and are asymptotically normally distributed under suitable assumptions on X and Y (Hannah; 1970). When the series are indeed independent, the normality assumption is no longer required (Haugh and Box, 1977) but analyst may still be misled in the interpretation of the cross-correlation estimates by attributing some significance to the apparent patterns in the cross-correlation function, which infact are as a result of sampling properties of the estimates used (Box and newbold 1971). Alternatively if the series X and Y are each white noise, then the Bartlet (1946) expression of covariance between two cross-correlation estimates becomes simplified and it will be quite easy to interpret the cross-correlation estimates only in the situation of the independent white noise series. Fortunately, this latter situation is of practical importance because at the identification stage of the model building process, one is often interested in comparing these cross-correlation estimates with bench marks appropriate to the null hypothesis of series independence and more importantly to know when cutoff takes place.To decide whether
and are asymptotically normally distributed under suitable assumptions on X and Y (Hannah; 1970). When the series are indeed independent, the normality assumption is no longer required (Haugh and Box, 1977) but analyst may still be misled in the interpretation of the cross-correlation estimates by attributing some significance to the apparent patterns in the cross-correlation function, which infact are as a result of sampling properties of the estimates used (Box and newbold 1971). Alternatively if the series X and Y are each white noise, then the Bartlet (1946) expression of covariance between two cross-correlation estimates becomes simplified and it will be quite easy to interpret the cross-correlation estimates only in the situation of the independent white noise series. Fortunately, this latter situation is of practical importance because at the identification stage of the model building process, one is often interested in comparing these cross-correlation estimates with bench marks appropriate to the null hypothesis of series independence and more importantly to know when cutoff takes place.To decide whether 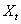 series and the historical values of
series and the historical values of 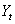 cause
cause 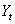 it is appealing to consider whether or not the residuals
it is appealing to consider whether or not the residuals 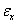 and
and 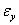 are related. Haugh and Box (1977) relates
are related. Haugh and Box (1977) relates 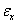 and
and 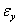 under the assumption that X and Y are independent; the autocorrelation function of the white noise series
under the assumption that X and Y are independent; the autocorrelation function of the white noise series 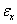 and
and 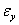 are particularly simple and the specification of the model connecting these series depends on the appearance of the cross-correlation function for the bivariate process which may be individually autocorrelated.In general linear process the random terms of different observations are assumed to be independent, this means that all the covariances of any
are particularly simple and the specification of the model connecting these series depends on the appearance of the cross-correlation function for the bivariate process which may be individually autocorrelated.In general linear process the random terms of different observations are assumed to be independent, this means that all the covariances of any 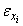 with any other
with any other 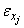 should be zero. But situation arises when the value which the random term
should be zero. But situation arises when the value which the random term 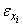 assumed depends on the value which
assumed depends on the value which 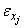 assumed, this is pure violation of the assumptions underlying general linear process (See Walter 2010).This study specifically aims at providing covariance structures that links
assumed, this is pure violation of the assumptions underlying general linear process (See Walter 2010).This study specifically aims at providing covariance structures that links 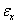 and
and 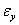 to express the real relationship that exists between endogenous and exogenous variables in the presence of autocorrelated residuals or disturbance terms. We shall specifically consider two stage procedure, such that at the first stage the residual series for each of the observed series X and Y are generated using admissible time domain model adjusted for autocorrelations in their residuals, while at the second stage when no significant cross-correlation occurs at non-negative lags between
to express the real relationship that exists between endogenous and exogenous variables in the presence of autocorrelated residuals or disturbance terms. We shall specifically consider two stage procedure, such that at the first stage the residual series for each of the observed series X and Y are generated using admissible time domain model adjusted for autocorrelations in their residuals, while at the second stage when no significant cross-correlation occurs at non-negative lags between 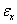 and
and 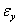 a complete model for X and Y as specified and the level of causality is then identified.
a complete model for X and Y as specified and the level of causality is then identified.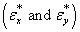 are then cross-correlated in the usual way and a tentative dynamic shock model is identified which relates
are then cross-correlated in the usual way and a tentative dynamic shock model is identified which relates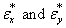 . By combining the univariate model for series
. By combining the univariate model for series  and
and  with the identified model connecting
with the identified model connecting 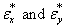 , we then identify a distributed lag model relating
, we then identify a distributed lag model relating 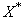 and
and 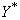 .
.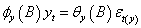
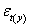 is the residual term,
is the residual term, 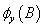 = 1-
= 1- 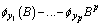 and
and 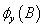 =
= 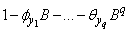 ; similarly we write the residual series
; similarly we write the residual series 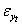 driving X as
driving X as 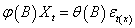
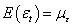 (usually assumed to be zero), a finite constant variance
(usually assumed to be zero), a finite constant variance 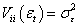 and covariance
and covariance 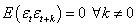 .At the first stage, assuming X and Y are individually and jointly covariance stationary series, it is possible to model each series individually as:
.At the first stage, assuming X and Y are individually and jointly covariance stationary series, it is possible to model each series individually as: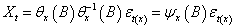
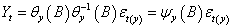
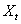 is
is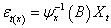
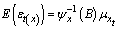 ,
,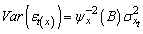 and for autocorrelation we have
and for autocorrelation we have 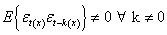 . Similarly, the residual series for
. Similarly, the residual series for 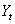 is
is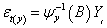
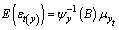
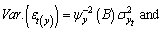
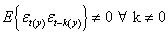 To test for dependence in the disturbance terms we use the asymptotic or large sample test statistic, this states that under null hypothesis of no serial correlation it can be shown that having fitted the model
To test for dependence in the disturbance terms we use the asymptotic or large sample test statistic, this states that under null hypothesis of no serial correlation it can be shown that having fitted the model 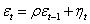
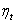 is normally distributed with zero mean and constant variance; then
is normally distributed with zero mean and constant variance; then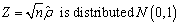 . If the absolute value of Z exceeds the critical value at the chosen level of significance, we reject the null hypothesis.At the second stage, the disturbances
. If the absolute value of Z exceeds the critical value at the chosen level of significance, we reject the null hypothesis.At the second stage, the disturbances 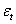 are unobservable and the nature of serial correlation is often a matter of speculation or practical exigencies. In practice, it is usually assumed that the
are unobservable and the nature of serial correlation is often a matter of speculation or practical exigencies. In practice, it is usually assumed that the 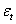 follows the first- order autoregressive process defined as
follows the first- order autoregressive process defined as 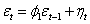
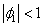 and the
and the 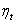 follows the ordinary least squares assumptions of zero expected value; constant variance and none autocorrelation.Assuming the validity of equation (8), the serial correlation problem can be resolved if
follows the ordinary least squares assumptions of zero expected value; constant variance and none autocorrelation.Assuming the validity of equation (8), the serial correlation problem can be resolved if 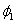 is known or estimated. To see this, assume the model structure defined in equation (3), that is
is known or estimated. To see this, assume the model structure defined in equation (3), that is 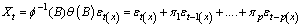
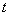 , then it is true for
, then it is true for 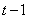 , and
, and 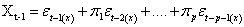
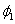 and subtracting the result from (9) gives
and subtracting the result from (9) gives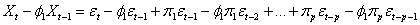
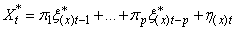
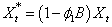 and
and 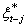
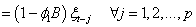 Since
Since 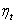 satisfy all the assumptions of general linear model, one can proceed to apply OLS to the adjusted series
satisfy all the assumptions of general linear model, one can proceed to apply OLS to the adjusted series 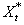 and
and 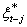 to give estimators of the dynamic model parameters, these estimators will all have optimum properties of BLUE. We can express equation (12) for the output series as
to give estimators of the dynamic model parameters, these estimators will all have optimum properties of BLUE. We can express equation (12) for the output series as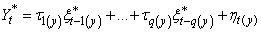
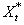 and
and 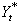 given in equations (12) and (13) are jointly covariance stationary series; then we have
given in equations (12) and (13) are jointly covariance stationary series; then we have 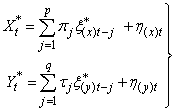
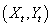 are independent, the covariance structure of
are independent, the covariance structure of 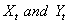 defined in equations (3) and (4) may be written as:
defined in equations (3) and (4) may be written as:
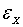 and
and 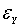 is not bivariate white noise, because the
is not bivariate white noise, because the 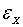 and
and 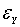 may be correlated as non-zero lags, that
may be correlated as non-zero lags, that 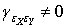 exist
exist 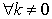 since this may arise, one could suspect autocorrelation in residuals. Equation (14) could provide the covariance structure of
since this may arise, one could suspect autocorrelation in residuals. Equation (14) could provide the covariance structure of 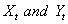 in terms of uncorrelated residuals
in terms of uncorrelated residuals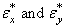 , the covariances are derived as follows:
, the covariances are derived as follows: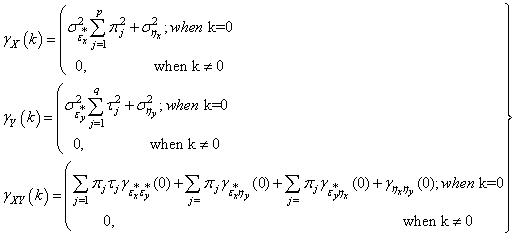
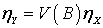
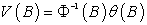 . The model described in equation (17) is a modified version of what was given by Box and Jenkins (1976, page 380). By using the structural form on equation (14) in (17) we have:
. The model described in equation (17) is a modified version of what was given by Box and Jenkins (1976, page 380). By using the structural form on equation (14) in (17) we have: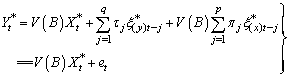
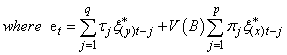 Equation (18) gives a measure of causal effect of X-input series on Y-output series. Similarly, a measure of causal effect of
Equation (18) gives a measure of causal effect of X-input series on Y-output series. Similarly, a measure of causal effect of 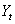 on
on 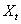 could be obtained as: Let the fitted model between
could be obtained as: Let the fitted model between 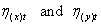 be
be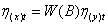 , then the causality measure is
, then the causality measure is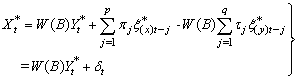
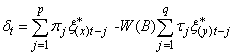 . The latter parts of equations (18) and (19) would be compared with the conventional dynamic distributed lag model:
. The latter parts of equations (18) and (19) would be compared with the conventional dynamic distributed lag model: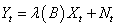
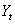 and
and 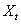 are related with autocorrelated residuals in the form described in equations (3) and (4) and that
are related with autocorrelated residuals in the form described in equations (3) and (4) and that 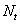 is assumed to be autocorrelated residuals which are linearly independent of input series
is assumed to be autocorrelated residuals which are linearly independent of input series 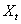 described in equation (20).
described in equation (20).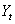 ) and leading indicator (
) and leading indicator (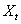 ) collected over 150 time points. The series are individually verified for unit root using Augmented Dickey Fuller (ADF) test statistic. In table 1 (see appendix), the null hypothesis of the presence of unit root is not rejected for both series as indicated by the value of ADF test statistic. These series are the differenced once; the values of ADF test statistic displayed in table 2 indicate that both series are stationary. We observe using the correlogram plot (see figures 1 and 2 in appendix) that autoregressive model of order one is appropriate for the difference series. The models fitted are:
) collected over 150 time points. The series are individually verified for unit root using Augmented Dickey Fuller (ADF) test statistic. In table 1 (see appendix), the null hypothesis of the presence of unit root is not rejected for both series as indicated by the value of ADF test statistic. These series are the differenced once; the values of ADF test statistic displayed in table 2 indicate that both series are stationary. We observe using the correlogram plot (see figures 1 and 2 in appendix) that autoregressive model of order one is appropriate for the difference series. The models fitted are: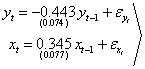
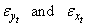 in equation (21) are verified for serial correlation using the large sample test statistic described in section 2 above. In table 2, we confirm that these residuals are individually stationary, serially correlated and normally distributed. Hence we transformed both the sales and leading indicator series using
in equation (21) are verified for serial correlation using the large sample test statistic described in section 2 above. In table 2, we confirm that these residuals are individually stationary, serially correlated and normally distributed. Hence we transformed both the sales and leading indicator series using 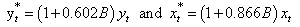 respectively. The autoregressive models of order one fitted to the transformed series are:
respectively. The autoregressive models of order one fitted to the transformed series are: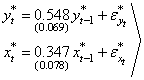
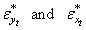 defined in equation (22) are individually stationary, serially non-correlated and normally distributed as indicated by the values of ADF, Z and Jarque-Bera (JB) statistics. The dynamic model between
defined in equation (22) are individually stationary, serially non-correlated and normally distributed as indicated by the values of ADF, Z and Jarque-Bera (JB) statistics. The dynamic model between 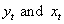 without adjusting for the effect of serial correlation in their errors is obtained thus:
without adjusting for the effect of serial correlation in their errors is obtained thus: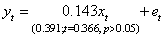


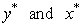 is:
is: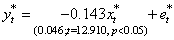
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML