-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(3): 95-98
doi:10.5923/j.ajms.20130303.01
Marginal Asymmetry Measure Based on Entropy for Square Contingency Tables with Ordered Categories
Kouji Tahata, Takuya Yoshimoto, Sadao Tomizawa
Department of Information Sciences, Tokyo University of Science, Noda City, Chiba, 278-8510, Japan
Correspondence to: Kouji Tahata, Department of Information Sciences, Tokyo University of Science, Noda City, Chiba, 278-8510, Japan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
For the analysis of square contingency tables, Tomizawa, Miyamoto and Ashihara (2003) considered a measure to represent the degree of departure from marginal homogeneity. The measure lies between 0 and 1, and it takes the minimum value when the marginal homogeneity holds and the maximum value when one of two symmetric cumulative probabilities for any category is zero. This paper proposes improvement of the measure so that the degree of departure from marginal homogeneity can attain the maximum value even when the cumulative probabilities are not zero. The proposed measure would be useful for representing the degree of departure from marginal homogeneity, especially when some asymmetry models hold as the extended marginal homogeneity model or the conditional symmetry model. Examples are given.
Keywords: Kullback-Leibler information, Measure, Power-divergence, Shannon entropy
Cite this paper: Kouji Tahata, Takuya Yoshimoto, Sadao Tomizawa, Marginal Asymmetry Measure Based on Entropy for Square Contingency Tables with Ordered Categories, American Journal of Mathematics and Statistics, Vol. 3 No. 3, 2013, pp. 95-98. doi: 10.5923/j.ajms.20130303.01.
Article Outline
1. Introduction
- Consider an
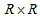 square contingency table with the same row and column classifications. Let
square contingency table with the same row and column classifications. Let 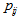 denote the probability that an observation will fall in the
denote the probability that an observation will fall in the  th row and
th row and 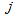 th column of the table (
th column of the table (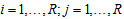 ), and let
), and let 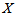 and
and 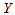 denote the row and column variables, respectively. The marginal homogeneity (MH) model is defined by
denote the row and column variables, respectively. The marginal homogeneity (MH) model is defined by 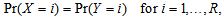 namely
namely 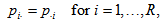 where
where 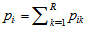 and
and 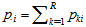 (see, for example, Stuart, 1955; Bishop, Fienberg and Holland, 1975, p.293). Let
(see, for example, Stuart, 1955; Bishop, Fienberg and Holland, 1975, p.293). Let 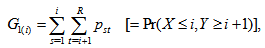 and
and 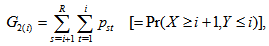 for
for 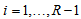 . By considering the difference between the
. By considering the difference between the 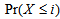 and
and 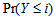 , the MH model also be expressed as
, the MH model also be expressed as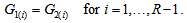 Namely, this states that the cumulative probability that an observation will fall in row category
Namely, this states that the cumulative probability that an observation will fall in row category 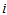 or below and column category
or below and column category 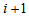 or above is equal to the cumulative probability that the observation falls in column category
or above is equal to the cumulative probability that the observation falls in column category 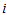 or below and row category
or below and row category 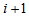 or above for
or above for 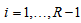 . When the MH model does not hold, we are interested in measuring the degree of departure from MH. For square contingency tables with ordered categories, Tomizawa, Miyamoto and Ashihara (2003) proposed the measure (denoted by
. When the MH model does not hold, we are interested in measuring the degree of departure from MH. For square contingency tables with ordered categories, Tomizawa, Miyamoto and Ashihara (2003) proposed the measure (denoted by 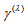 in Section 2) to represent the degree of departure from MH. The measure
in Section 2) to represent the degree of departure from MH. The measure 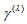 ranges between
ranges between 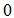 and
and 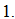 Also, (i)
Also, (i) 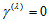 if and only if the MH model holds, and (ii)
if and only if the MH model holds, and (ii) 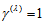 if and only if the degree of departure from MH is a maximum; that is,
if and only if the degree of departure from MH is a maximum; that is, 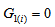 (then
(then 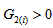 ) or
) or 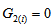 (then
(then 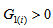 ) for all
) for all 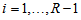 . However, for the analysis of square contingency tables, all cell probabilities
. However, for the analysis of square contingency tables, all cell probabilities 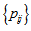 are positive in many cases. Thus, the measure
are positive in many cases. Thus, the measure 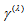 may be unsuitable for such data, because the measure
may be unsuitable for such data, because the measure 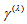 cannot attain the maximum value. So, we are now interested in the measure to represent the degree of departure from MH such that it can attain the maximum value even when each of cell probabilities
cannot attain the maximum value. So, we are now interested in the measure to represent the degree of departure from MH such that it can attain the maximum value even when each of cell probabilities 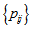 is not zero. Yamamoto, Masumura and Tomizawa (2011) considered such a measure for nominal square table. We are now interested in proposing such a measure for ordinal square table. The purpose of this paper is to consider an improvement of measure for square contingency tables with ordered categories when all cell probabilities
is not zero. Yamamoto, Masumura and Tomizawa (2011) considered such a measure for nominal square table. We are now interested in proposing such a measure for ordinal square table. The purpose of this paper is to consider an improvement of measure for square contingency tables with ordered categories when all cell probabilities 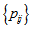 are positive.
are positive.2. Improved Measure for Marginal Homogeneity
- Consider an
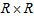 table with ordered categories. Assume that
table with ordered categories. Assume that 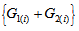 are positive. Let
are positive. Let 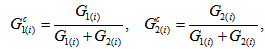 for
for 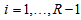 ; and let
; and let 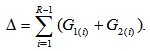 For a specified
For a specified 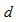 which satisfies
which satisfies 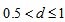 and
and 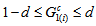 for all
for all 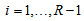 , consider a measure defined by
, consider a measure defined by 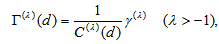 where
where 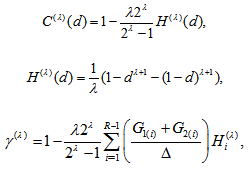 with
with 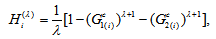 and the value at
and the value at 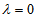 is taken to be the limit as
is taken to be the limit as  . Thus,
. Thus, 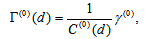 where
where 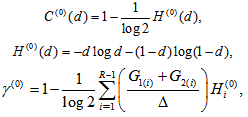 with
with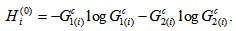 Note that
Note that 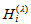 is the diversity index proposed by Patil and Taillie (1982), which includes the Shannon entropy when
is the diversity index proposed by Patil and Taillie (1982), which includes the Shannon entropy when 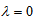 . When
. When 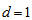 , then
, then 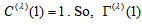 is identical to the measure
is identical to the measure 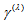 given by Tomizawa et al. (2003). Since
given by Tomizawa et al. (2003). Since 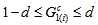 , the minimum value of
, the minimum value of 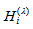 is
is 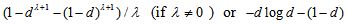
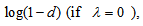 and the maximum value of it is
and the maximum value of it is 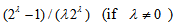 or
or 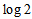 (if
(if 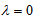 ) when
) when 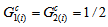 for all
for all 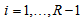 . So, when
. So, when 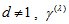 cannot attain the value 1. The proposed measure
cannot attain the value 1. The proposed measure 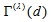 with
with 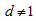 is modified by using modification coefficient
is modified by using modification coefficient 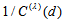 such that the measure
such that the measure 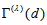 can attain the value
can attain the value 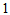 . If all
. If all 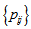 are positive, then
are positive, then 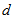 must be taken as
must be taken as 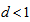 . Moreover, for each
. Moreover, for each 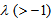 and a fixed
and a fixed 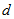 , the measure
, the measure 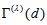 has characteristics that (i)
has characteristics that (i) 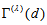 must lie between
must lie between 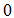 and
and 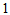 , (ii)
, (ii) 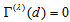 if and only if the MH model holds, i.e.,
if and only if the MH model holds, i.e., 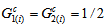 for all
for all 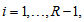 and (iii)
and (iii) 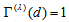 if and only if the degree of departure from MH is the largest in the sense that
if and only if the degree of departure from MH is the largest in the sense that 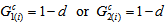 for all
for all 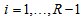 . The measure also may be expressed as, for
. The measure also may be expressed as, for 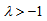
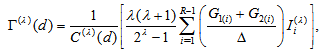 where
where 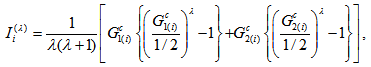 especially
especially 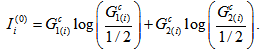 Note that
Note that 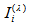 is the power-divergence between
is the power-divergence between 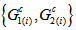 and
and 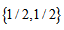 (Cressie and Read, 1984) which includes the Kullback-Leibler information when
(Cressie and Read, 1984) which includes the Kullback-Leibler information when 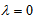 .
. 3. Approximate Confidence Interval for Measure
- Let
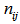 denote the observed frequency in the
denote the observed frequency in the 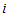 th row and
th row and 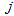 th column of the table (
th column of the table (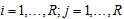 ). Assume that a multinomial distribution applies to the
). Assume that a multinomial distribution applies to the 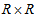 table. The sample version of
table. The sample version of 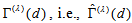 , is given by
, is given by 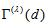 with
with 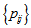 replaced by
replaced by 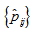 , where
, where 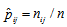 and
and 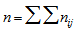 . Using the delta method (Bishop et al., 1975, Sec. 14.6),
. Using the delta method (Bishop et al., 1975, Sec. 14.6), 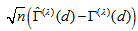 has asymptotically (as
has asymptotically (as 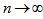 ) a normal distribution with mean zero and variance
) a normal distribution with mean zero and variance 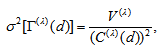 where for
where for 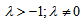
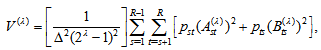 with
with 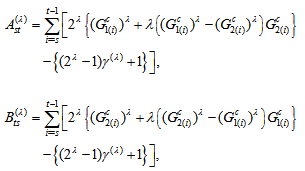 and the value of variance at
and the value of variance at 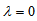 is taken to be the limit as
is taken to be the limit as 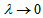 . Let
. Let 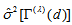 denote
denote 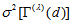 with
with 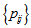 replaced by
replaced by 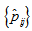 . Using this result, the estimated approximate confidence interval for the measure
. Using this result, the estimated approximate confidence interval for the measure 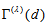 is obtained.
is obtained. 4. Examples
- Consider the data in Table 1, taken from Andersen (1997, p.226). These data show the forecasts for production and prices for the coming three year periods given by experts in July 1956 and the actual production figures for production and prices in May 1959 given from Danish factories. For these data, the cell probabilities
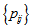 are theoretically positive (not zero). Thus, it may be irrelevance to use the measure
are theoretically positive (not zero). Thus, it may be irrelevance to use the measure 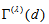 with
with 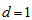 . So we should use the measure
. So we should use the measure 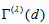 with
with 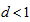 (for example,
(for example, 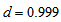 ) so that the measure can attain the maximum value 1.
) so that the measure can attain the maximum value 1.
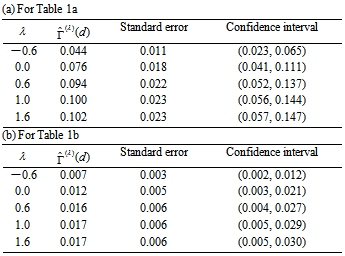
|
|
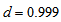 and
and 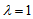 , the estimated measure
, the estimated measure 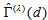 is
is 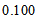 for Table 1a and
for Table 1a and 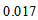 for Table 1b from Tables 2a and 2b. Thus, (i) for Table 1a, the degree of departure from MH is estimated to be
for Table 1b from Tables 2a and 2b. Thus, (i) for Table 1a, the degree of departure from MH is estimated to be 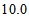 percent of the maximum degree of departure from MH and (ii) for Table 1b, it is estimated to be
percent of the maximum degree of departure from MH and (ii) for Table 1b, it is estimated to be 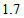 percent of the maximum. Furthermore, we see from Tables 2a and 2b that the degree of departure from MH is greater for Table 1a than for Table 1b because the values in the confidence intervals for
percent of the maximum. Furthermore, we see from Tables 2a and 2b that the degree of departure from MH is greater for Table 1a than for Table 1b because the values in the confidence intervals for 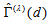 are greater for Table 1a than for Table 1b.
are greater for Table 1a than for Table 1b.5. Discussion
- Consider the extended MH (EMH) model defined by
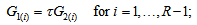 also see Tahata and Tomizawa (2008). A special case of EMH model obtained by putting
also see Tahata and Tomizawa (2008). A special case of EMH model obtained by putting 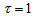 is the MH model. When the EMH model holds, the proposed measure
is the MH model. When the EMH model holds, the proposed measure 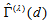 is expressed as
is expressed as 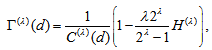 | (1) |
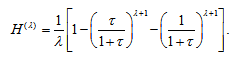 For
For 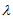 fixed and
fixed and 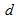 fixed,
fixed, 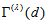 increases as
increases as 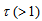 increases (or as
increases (or as 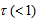 decreases). Especially, when
decreases). Especially, when 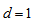 ,
, 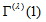 is identical to
is identical to 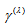 proposed by Tomizawa et al. (2003). When the EMH model holds,
proposed by Tomizawa et al. (2003). When the EMH model holds, 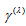 approaches 1 as
approaches 1 as 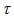 approaches infinity or zero. However, when the EMH model holds,
approaches infinity or zero. However, when the EMH model holds, 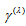 cannot attain 1 because then
cannot attain 1 because then 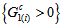 and
and 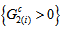 , namely there is not the structure of
, namely there is not the structure of 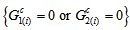 being the condition of
being the condition of 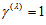 . The measure
. The measure 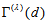 with
with 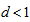 can attain the maximum value 1 even if
can attain the maximum value 1 even if 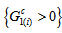 and
and 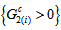 for all
for all 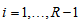 . Therefore, the measure
. Therefore, the measure 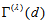 with
with 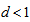 rather than
rather than 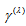 may be appropriate when the EMH model holds. Also since the probabilities
may be appropriate when the EMH model holds. Also since the probabilities 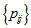 are positive (not zero), the measure
are positive (not zero), the measure  with
with 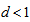 rather than
rather than 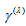 would be appropriate to represent the degree of departure from the MH toward the structure of maximum departure from MH which can be defined actually.The conditional symmetry (CS) model (McCullagh, 1978) is defined by
would be appropriate to represent the degree of departure from the MH toward the structure of maximum departure from MH which can be defined actually.The conditional symmetry (CS) model (McCullagh, 1978) is defined by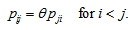 A special case of this model obtained by putting
A special case of this model obtained by putting 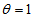 is the symmetry model (Bowker, 1948). If the symmetry model holds, then the MH model holds. Also if the CS model holds, then the EMH model holds. Therefore when the CS model holds, the measure
is the symmetry model (Bowker, 1948). If the symmetry model holds, then the MH model holds. Also if the CS model holds, then the EMH model holds. Therefore when the CS model holds, the measure 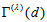 is expressed by with
is expressed by with 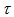 replaced by
replaced by 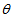 . Thus by the similar reason, when the CS model holds, the measure
. Thus by the similar reason, when the CS model holds, the measure 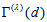 with
with 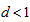 rather than
rather than 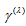 would be appropriate.
would be appropriate. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML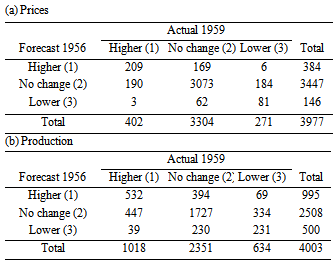
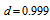 , the estimates of
, the estimates of 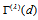 , estimated approximate standard error for
, estimated approximate standard error for 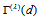 , and approximate 95% confidence interval for
, and approximate 95% confidence interval for 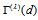 , applied to Tables 1a and 1b.
, applied to Tables 1a and 1b.