-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(2): 73-83
doi:10.5923/j.ajms.20130302.02
Graphical Interpretation of the New Sequence of Functions Involving Mittage-Leffler Function Using Matlab
Praveen Agarwal, Mehar Chand
Department of Mathematics Anand International College of Engineering, Jaipur-303012, India
Correspondence to: Praveen Agarwal, Department of Mathematics Anand International College of Engineering, Jaipur-303012, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The aim of the paper is an attempt to introduce a new sequence of functions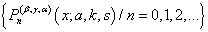 , which involving the Mittage-Leffler function
, which involving the Mittage-Leffler function 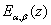 by using operational technique. Some interesting generating relations are obtained in sections 2. The remarkable thing of this paper is the crucial MATLAB coding of the new sequence of functions, Database and Graph established using the MATLAB (R2012a) in the section (4) and (5) for different values of parameters and n=1, 2, 3. The reader can establish Database and Graph using the same program for any value of n.
by using operational technique. Some interesting generating relations are obtained in sections 2. The remarkable thing of this paper is the crucial MATLAB coding of the new sequence of functions, Database and Graph established using the MATLAB (R2012a) in the section (4) and (5) for different values of parameters and n=1, 2, 3. The reader can establish Database and Graph using the same program for any value of n.
Keywords: Mittag-Leffler Function, Generating Relation, Sequence of Functions, Operational Techniques Matlab
Cite this paper: Praveen Agarwal, Mehar Chand, Graphical Interpretation of the New Sequence of Functions Involving Mittage-Leffler Function Using Matlab, American Journal of Mathematics and Statistics, Vol. 3 No. 2, 2013, pp. 73-83. doi: 10.5923/j.ajms.20130302.02.
Article Outline
1. Introduction
- MATLAB is a high-performance language for technical computing. It integrates computation, visualization, and programming in an easy-to-use environment where problems and solutions are expressed in familiar mathematical notation. Typical uses include:● Math and computation● Algorithm development● Modeling, simulation, and prototyping● Data analysis, exploration, and visualization● Scientific and engineering graphics● Application development, including Graphical User Interface buildingIn pure mathematics, since Matlab is an integrated computer software which has three functions: symbolic computing, numerical computing and graphics drawing. Matlab is capable to carry out many functions including computing polynomials and rational polynomials, solving equations and computing many kind of mathematical expressions. One can also use Matlab to calculate the limit, derivative, integral and Taylor series of some mathematical expressions. With Matlab, The graphs of functions with one or two variables can be easily drawn in selected domain. Therefore, functions can be studied by visualization for their main Characteristics. Matlab is also a system which can be easily expanded. Matlab provides many powerful software packages which can be easily incorporated into the clients system. Recently, there are many papers in the literature which are devoted to the application of Matlab in mathematical analysis, see the work of Stephen (2006), Dunn (2003), Shampine and Robert (2005).The distinct scientific communities that are working on various aspects of automatic analysis of data include Combinatorial Pattern Matching, Data Mining, Computational Statistics, Network Analysis, Text Mining, Image Processing, Syntactical Pattern Recognition, Machine Learning, Statistical Pattern Recognition, Computer Vision, and many others. The special function
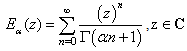 | (1) |
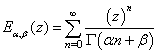
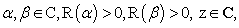 | (2) |
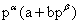 certain boundary value problems involving fractional integro-differential equations of Volterra type (Samko et al., 1993). During the various developments of fractional calculus in the last four decades this function has gained importance and popularity on account of its vast applications in the fields of science and engineering. Hille and Tamarkin (1930) have presented a solution of the Abel-Volterra type equation in terms of Mittag-Leffler function. During the last 15 years the interest in Mittag-Leffler function and Mittag-Leffler type functions is considerably increased among engineers and scientists due to their vast potential of applications in several applied problems, such as fluid flow, rheology, diffusive transport akin to diffusion, electric networks, probability, statistical distribution theory etc. For a detailed account of various properties, generalizations, and application of this function, the reader may refer to earlier important works of Blair (1974), Bagley and Torvik (1984), Caputo and Mainardi (1971), Dzherbashyan (1966), Gorenflo and Vessella (1991), Gorenflo and Rutman (1994), Kilbas and Saigo (1995), Gorenflo et al. (1997), Gorenflo and Mainardi (1994, 1996, 1997), Gorenflo, Luchko and Rogosin (1997), Gorenflo, Kilbas and Rogosin (1998), Luchko (1999), Luchko and Srivastava (1995), Kilbas, Saigo and Saxena (2002, 2004), Saxena and Saigo (2005), Kiryakova (2008a, 2008b), Saxena, Kalla and Kiryakova (2003), Saxena, Mathai and Haubold (2002, 2004, 2004a, 2004b, 2006), Saxena and Kalla (2008), Mathai, Saxena and Haubold (2006), Haubold andMathai (2000), Haubold, Mathai and Saxena (2007), Srivastava and Saxena (2001), and others.Operational techniques have drawn the attention of several researchers in the study of sequences of functions and polynomials. In this paper, we introduce a new sequence of functions
certain boundary value problems involving fractional integro-differential equations of Volterra type (Samko et al., 1993). During the various developments of fractional calculus in the last four decades this function has gained importance and popularity on account of its vast applications in the fields of science and engineering. Hille and Tamarkin (1930) have presented a solution of the Abel-Volterra type equation in terms of Mittag-Leffler function. During the last 15 years the interest in Mittag-Leffler function and Mittag-Leffler type functions is considerably increased among engineers and scientists due to their vast potential of applications in several applied problems, such as fluid flow, rheology, diffusive transport akin to diffusion, electric networks, probability, statistical distribution theory etc. For a detailed account of various properties, generalizations, and application of this function, the reader may refer to earlier important works of Blair (1974), Bagley and Torvik (1984), Caputo and Mainardi (1971), Dzherbashyan (1966), Gorenflo and Vessella (1991), Gorenflo and Rutman (1994), Kilbas and Saigo (1995), Gorenflo et al. (1997), Gorenflo and Mainardi (1994, 1996, 1997), Gorenflo, Luchko and Rogosin (1997), Gorenflo, Kilbas and Rogosin (1998), Luchko (1999), Luchko and Srivastava (1995), Kilbas, Saigo and Saxena (2002, 2004), Saxena and Saigo (2005), Kiryakova (2008a, 2008b), Saxena, Kalla and Kiryakova (2003), Saxena, Mathai and Haubold (2002, 2004, 2004a, 2004b, 2006), Saxena and Kalla (2008), Mathai, Saxena and Haubold (2006), Haubold andMathai (2000), Haubold, Mathai and Saxena (2007), Srivastava and Saxena (2001), and others.Operational techniques have drawn the attention of several researchers in the study of sequences of functions and polynomials. In this paper, we introduce a new sequence of functions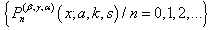 , which involving the Mittage-Leffler function
, which involving the Mittage-Leffler function 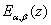 in equation (17) by using operational technique. Some interesting generating relations are obtained in sections 2. The remarkable thing of this paper is the crucial MATLAB coding of the new sequence of functions, Database and Graph established by using the MATLAB (R2012a) in the section (4) and (5) for different values of parameters and n=1, 2, 3. The reader can establish Database and Graph using the same program for any value of n.In 1956, Chak defined a class of polynomials as,
in equation (17) by using operational technique. Some interesting generating relations are obtained in sections 2. The remarkable thing of this paper is the crucial MATLAB coding of the new sequence of functions, Database and Graph established by using the MATLAB (R2012a) in the section (4) and (5) for different values of parameters and n=1, 2, 3. The reader can establish Database and Graph using the same program for any value of n.In 1956, Chak defined a class of polynomials as,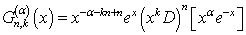 | (3) |
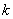 is constant and
is constant and 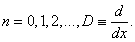 Gould and Hopper (1962) introduced generalized Hermite polynomials as,
Gould and Hopper (1962) introduced generalized Hermite polynomials as,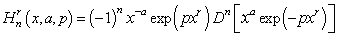 | (4) |
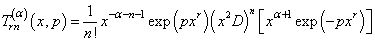 | (5) |
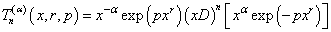 | (6) |
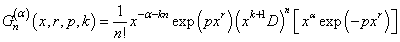 | (7) |
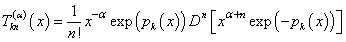 | (8) |
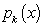 is a polynomial in
is a polynomial in 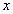 of degree
of degree 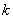 .Mittal (1971a) also proved following relation for (8) as,
.Mittal (1971a) also proved following relation for (8) as,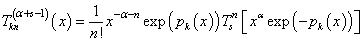 | (9) |
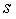 is constant and
is constant and 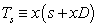 .Recently, Shukla and Prajapati (2007) obtained several properties of (9).Chandel (1973) also studied a class of polynomials defined as:
.Recently, Shukla and Prajapati (2007) obtained several properties of (9).Chandel (1973) also studied a class of polynomials defined as: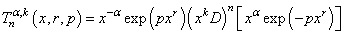 | (10) |
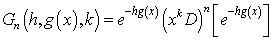 | (11) |
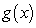 is a function of
is a function of 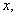
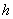 and
and 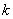 are constants.In the same year, Srivastava (1974) discussed some operational formulas generalized function
are constants.In the same year, Srivastava (1974) discussed some operational formulas generalized function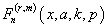 in the form,
in the form,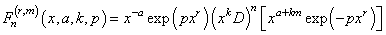 | (12) |
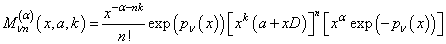 | (13) |
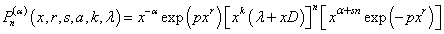 | (14) |
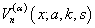 defined as:
defined as: 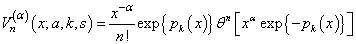 | (15) |
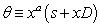 , where
, where 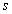 is constant and
is constant and 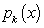 is a polynomial in
is a polynomial in 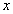 of degree
of degree 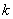 .J.C. Parjapati and N.K. Ahudia (Accepted on: 27.08.2012) introduced the sequence of function defined as,
.J.C. Parjapati and N.K. Ahudia (Accepted on: 27.08.2012) introduced the sequence of function defined as,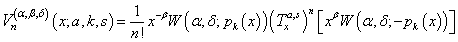 | (16) |
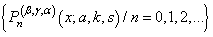 is introduced in this paper as:
is introduced in this paper as: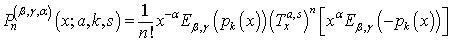 | (17) |
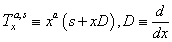 ,
, 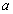 and
and 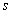 are constants,
are constants, 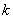 is finite and non-negative integer,
is finite and non-negative integer, 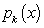 is a polynomial in
is a polynomial in 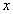 of degree
of degree 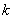 and
and 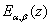 is a Mittage-Muffler function defined in equation (2).Some generating relations of class of polynomials or sequence of function have been obtained by using the properties of the differential operators.
is a Mittage-Muffler function defined in equation (2).Some generating relations of class of polynomials or sequence of function have been obtained by using the properties of the differential operators. 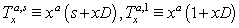 , where
, where 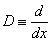 , is based on the work of Mittal (1977), Patil and Thakare (1975), Srivastava and Singh (1979).Some useful Operational Techniques are given below:
, is based on the work of Mittal (1977), Patil and Thakare (1975), Srivastava and Singh (1979).Some useful Operational Techniques are given below: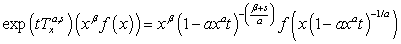 | (18) |
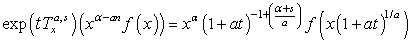 | (19) |
2. Generating Relations
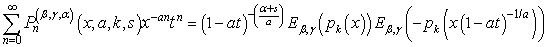 | (20) |
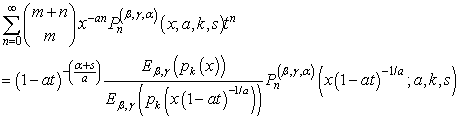 | (21) |
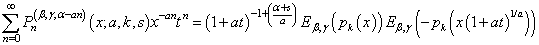 | (22) |
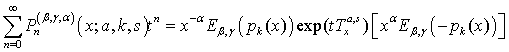 | (23) |
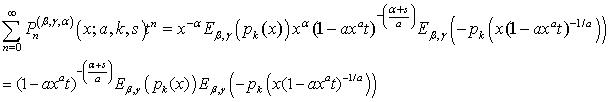 | (24) |
 by
by  , this gives (20).
, this gives (20).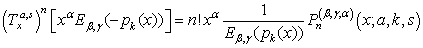 | (25) |
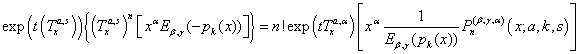
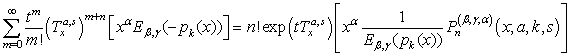 | (26) |
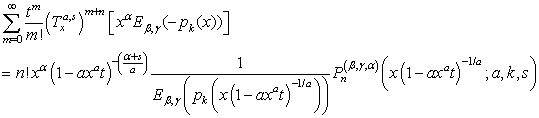 | (27) |
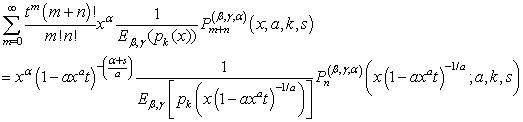 | (28) |
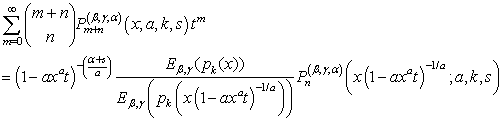 | (29) |
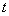 by
by 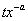 , this gives the result (21).Proof of (22)Again from (17), we have:
, this gives the result (21).Proof of (22)Again from (17), we have: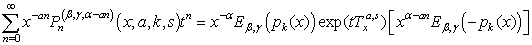 | (30) |
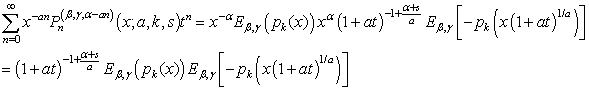 | (31) |
3. Special Cases
- The interesting special and particular cases between (17) and class of polynomials (3)-(17) can also be obtained for appropriate values of β, γ, α, a, k and s.The MATLAB is one of the important aspects mainly in the field of sciences and engineering, Therefore, the imperative MATLAB coding established for each parameter of equation (17) and some interesting Database and Graphs also established in the section 5. Using this coding reader may obtain large number of graphs of equation (17), which gives the eccentric characteristics in the area of sequence of functions or class of polynomials.
4. Programming of the New Sequence of Function in MATLAB
- Code is divided in parts as a new sequence of function is composition of two functions.Code of Generalized Mittage-Muffler function:function [E1] = GMLF(b,c,x)% GMLF returns sum(k=0:inf,(x^k/(gamma(kb+c))% Format of call: GMLF(b,c,x)syms xE1 = 1/gamma(c);for k=1:100E1 = E1 + (x.^k./gamma(b.*k+c));endendCode of New sequence of functions:function [Pn] = gnsGMLF1(beta,gamma,alpha,a,k,s,x)%Graph of Pn(beta,gamma,alpha,a,k,s,x)%MLF(a,b,x)=sum(k=0:inf,(gamma(a+k))x^k/(gamma(a))(k!*gamma(kb+c))%P=Pn(beta,gamma,alpha,a,k,s,x)=(1/n!)*x^-alpha*GMLF(beta,gamma,x^k)*Tn^(a,s)%(x^a*(s+x*D)(x^alpha)*GMLF(beta,gamma,-x^k)), where n=1,2,3,…syms x%n=input('please enter n:');%n=1;E1= GMLF(beta,gamma,-x.^k);y=(x.^alpha).*E1;for i=1:ny=(x.^a).*(s.*y+x.*diff(y));endE2=GMLF(beta,gamma,x.^k);v=(1./factorial(n)).*(1./(x.^alpha)).*E2.*y;%Pn=subs(v,x,-2:.5:2);Pn=subs(v,x);endPlot Graph:ezplot(gnsGMLFn(beta,gamma,alpha,a,k,s,x),[-2:.5:2])
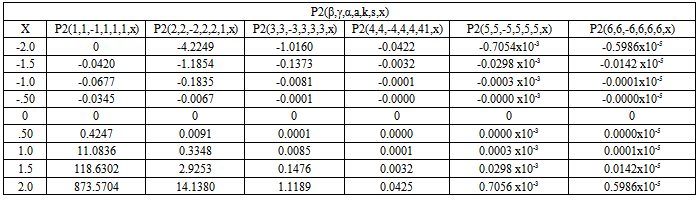
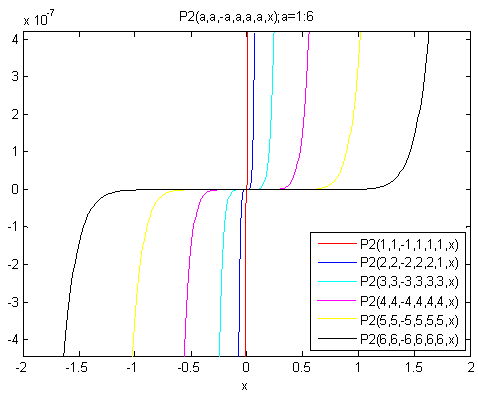
5. Different Databases and Graphs Using MATLAB
- The new sequence
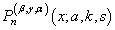 introduced in equation (17), takes place in the form of Pn(β,γ,α,a, k,s,x) to establish Database and Graph for different values of parameters β, γ, α, a, k, s and (n = 0, 1, 2, 3,…). We establish here four different Database for different values of parameters for n=1,2,3 in the interval
introduced in equation (17), takes place in the form of Pn(β,γ,α,a, k,s,x) to establish Database and Graph for different values of parameters β, γ, α, a, k, s and (n = 0, 1, 2, 3,…). We establish here four different Database for different values of parameters for n=1,2,3 in the interval  with difference .5, as shown in Database (a), (b), (c) & (d) and their corresponding Graphs are plotted.
with difference .5, as shown in Database (a), (b), (c) & (d) and their corresponding Graphs are plotted. First Database and Graph
 | Graph of the New Sequence based on Database (a) |
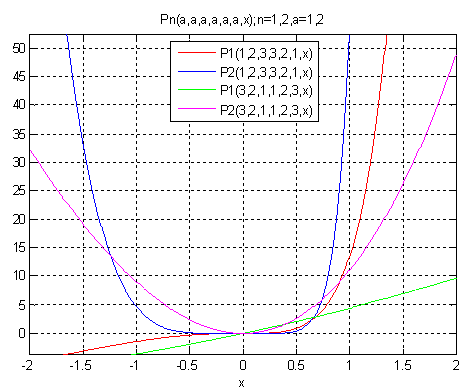 | Graph (a) |
Second Database and Graph
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
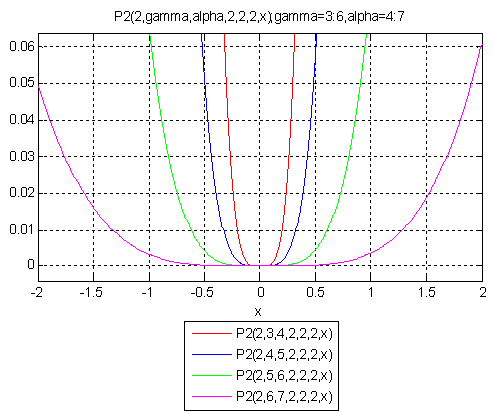 | Graph (b) |
Third Database and Graph
Fourth Database and Graph
| |||||||||||||||||||||||||||||||||||||||||||||||
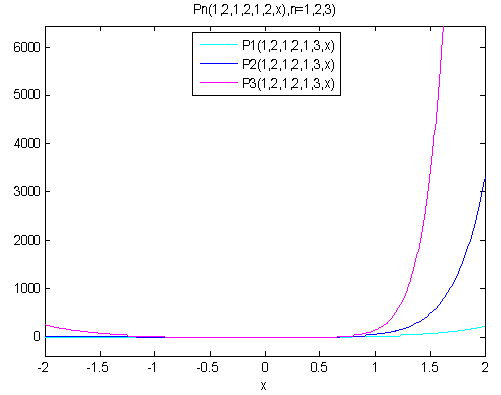 | Graph (d) |
6. Conclusions
- In the section (5), for the different values of parameters and value of n in the sequence of function
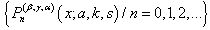 can easily interpreted and can be compared with the help of database and graph. The present paper has enabled us to find the trends of different functions in various ranges and have paved the way for comparison of trends.
can easily interpreted and can be compared with the help of database and graph. The present paper has enabled us to find the trends of different functions in various ranges and have paved the way for comparison of trends.
References
| [1] | Agarwal, R.P., (1953). A propos d’une note de M. Pierre Humbert, C.R. Acad. Sci. Paris, 236, 2031-2032. |
| [2] | Bagley, R.L. and Torvik, P.J., (1984). On the appearance of the fractional derivative in the behavior of real materials, Journal of Applied Mechanics, 51, 294-298. |
| [3] | Blair, G.W.S., (1974). Psychorheology: Links between the past and the present, Journal of Texture Studies, 5, 3-12. |
| [4] | Chak, A. M., (1956). A class of polynomials and generalization of stirling numbers, Duke J. Math., 23, 45-55. |
| [5] | Chandel, R.C.S., (1973). A new class of polynomials, Indian J. Math., 15(1), 41-49. |
| [6] | Chandel, R.C.S., (1974). A further note on the class of polynomials 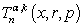 , Indian J. Math., 16(1), 39-48. , Indian J. Math., 16(1), 39-48. |
| [7] | Chatterjea, S. K., (1964). On generalization of Laguerre polynomials, Rend. Mat. Univ. Padova, 34, 180-190. |
| [8] | Caputo, M. and Mainardi, F., (1971). Linear models of dissipation in anelastic solids, Rivista del Nuovo Cimento, Ser. II, 1, 161-198. |
| [9] | Dunn, Peter K., (2003). Understanding statistics using computer demonstrations. Journal of Computers in Mathematics and Science Teaching, 22 (3). pp. 261-281. ISSN 0731-9258. |
| [10] | Dzherbashyan, M.M., (1966). Integral Transforms and Representations of Functions in the Complex Plane, Nauka, Moscow, (in Russian). |
| [11] | Erd´elyi, A., Magnus,W., Oberhettinger, F. and Tricomi, F. G. (1955). Higher Transcendental Functions,Vol. 3, McGraw - Hill, New York, Toronto and London. |
| [12] | E. Hille and J.D. Tamarkin, (1930). On the theory of linear integral equations, Annals of Mathematics, 31, 479-528. |
| [13] | Gorenflo, R., Kilbas, A.A. and Rogosin, S.V., (1998). On the generalized Mittag-Leffler type function, Integral Transforms and Special Functions, 7(3-4), 215-224. |
| [14] | Gorenflo, R. and Luchko, Yu. F., (1997). Operational methods for solving generalized Abel equations of second kind, Integral Transforms and Special Functions, 5, 47-58. |
| [15] | Gorenflo, R., Luchko, Yu. F. and Rogosin, S.V., (1997). Mittag-Leffler type functions, notes on growth properties and distribution of zeros, Preprint No. A04-97, Freie University of Berlin, Serie A Mathematik, Berlin. |
| [16] | Gorenflo, R. and Mainardi, F., (1994). Fractional oscillations and Mittag-Leffler functions, Preprint No. 1-14/96, Free University of Berlin, Berlin. |
| [17] | Gorenflo, R. and Mainardi, F., (1996). The Mittag-Leffler function in the Riemann-Liouville fractional calculus, In: A.A. Kilbas (ed) Boundary Value Problems, Special Functions and Fractional Calculus, Minsk, pp. 215-225. |
| [18] | Gorenflo, R. and Mainardi, F., (1997). Fractional calculus: integral and differential equations of fractional order, In: Fractals and Fractional Calculus in Continuum Mechanics (eds. A. Carpinteri and F. Mainardi), Springer-Verlag, Wien, pp.223-276. |
| [19] | Gorenflo, R. and Rutman, R., On ultraslow and intermediate processes, In: P. Rusev, I. Dimovski, V. Kiryakova (eds) Transform Methods and Special Functions, Sofia, 1994, 61-81, Science Culture Technology Publ., Singapore, 1995, pp.171-183. |
| [20] | Gorenflo, R. and Vessella, S., (1991). Abel Integral Equations: Analysis and Applications, Lecture Notes in Mathematics 1461, Springer-Verlag, Berlin. |
| [21] | Gould, H. W. and Hopper, A. T., (1962). Operational formulas connected with two generalizations of Hermite polynomials, Duck Math. J., 29, 51-63. |
| [22] | Haubold, H.J. and Mathai, A.M., (2000). The fractional kinetic equation and thermonuclear functions, Astrophysics and Space Science, 273, 53-63. |
| [23] | Haubold, H.J., Mathai, A.M. and Saxena, R.K., (2007). Solution of fractional reaction-diffusion equations in terms of the H-function, Bulletin of the Astronomical Society, India, 35, 681-689. |
| [24] | Humbert, P., (1953). Quelques resultants retifs a la fonction de Mittag-Leffler, C.R. Acad. Sci. Paris, 236, 1467-1468. |
| [25] | Humbert, P. and Agarwal, R.P., (1953). Sur la fonction de Mittag-Leffler et quelques unes de ses generalizations, Bull. Sci. Math., (Ser.II), 77, 180-185. |
| [26] | Hilfer, R. (ed.), (2000). Applications of Fractional Calculus in Physics, World Scientific, Singapore. |
| [27] | Joshi, C. M. and Prajapat, M. L., (1975). The operator 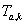 , and a generalization of certain classical polynomials, Kyungpook Math. J., 15, 191-199. , and a generalization of certain classical polynomials, Kyungpook Math. J., 15, 191-199. |
| [28] | Kilbas, A.A. and Saigo, M., (1995). On solutions of integral equations of Abel-Volterra type, Differential and Integral Equations, 8, 993-1011. |
| [29] | Kilbas, A.A., Saigo, M. and Saxena, R.K., (2004). Generalized Mittag-Leffler function and generalized fractional calculus operators, Integral Transforms and Special Functions, 15, 31-49. |
| [30] | Kilbas, A.A., Saigo, M. and Saxena, R.K., (2002). Solution of Volterra integro-differential equations with gen-eralized Mittag-Leffler function in the kernels, Journal of Integral Equations and Applications, 14(4), 377-386. |
| [31] | Kiryakova,V., (2008a). Some special functions related to fractional calculus and fractional non-integer order control systems and equations, Facta Universitatis Ser. Automatic Control and Robotics, Univ. Nis. |
| [32] | Kiryakova,V.S., (5-7 November 2008b). Special functions of fractional calculus: recent list, results, applications, 3rd IFC Workshop, FDA 08: Fractional Differentiation and its Applications, Cankaya University, Ankara, Turkey, pp.1-23. |
| [33] | Lang, K.R., (1999a). Astrophysical Formulae, Vol. 1: Radiation, Gas Processes and High-energy Astrophysics, 3rd edition, revised edition, Springer-Verlag, New York. |
| [34] | Lang, K.R., (1999b). Astrophysical Formulae, Vol. 2: Space, Time, Matter and Cosmology, Springer-Verlag, New York. |
| [35] | Luchko, Yu. F. and Gorenflo,R., (1999). An operational method for solving fractional differential equations with a Caputo derivative, Acta Mathematica Vietnam, 24, 207-234. |
| [36] | Luchko, Yu. F. and Srivastava, H.M., (1995). The exact solution of certain differential equations of fractional order by using fractional calculus, Computational Mathematics and Applications, 29, 73-85. |
| [37] | Mathai, A.M., Saxena, R.K. and Haubold, H.J., (2006). A certain class of Laplace transforms with application in reaction and reaction-diffusion equations, Astrophysics and Space Science, 305, 283-288. |
| [38] | Mittag-Leffler, G.M., (1903). Une generalisation de l’integrale de Laplace-Abel, C.R. Acad. Sci. Paris (Ser. II), 137, 537-539. |
| [39] | Mittag-Leffler, G.M., (1905). Sur la representation analytiqie d’une fonction monogene (cinquieme note), Acta Mathematica, 29, 101-181. |
| [40] | Mittal, H. B., (1971). A generalization of Laguerre polynomial, Publ. Math. Debrecen, 18, 53-58. |
| [41] | Mittal, H. B., (1971a). Operational representations for the generalized Laguerre polynomial, Glasnik Mat.Ser III, 26(6), 45-53. |
| [42] | Mittal, H. B., (1977). Bilinear and Bilateral generating relations, American J. Math., 99, 23-45. |
| [43] | Patil, K. R. and Thakare, N. K., (1975). Operational formulas for a function defined by a generalized Rodrigues formula-II, Sci. J. Shivaji Univ. 15, 1-10. |
| [44] | Prajapati, J.C. and Ajudia, N.K., (Accepted On: 27.08.2012). On New Sequence of Functions and Their MATLAB Computation, International Journal of Physical, Chemical & Mathematical Sciences, Vol. 1; No. 2: ISSN: 2278-683X. |
| [45] | Samko, S. G., Kilbas, A. A. and Marichev, O. I. (1993). Fractional Integrals and Derivatives. Yverdon, Switzerland: Gordon and Breach, pp. 21-22. |
| [46] | Saxena, R.K. and Kalla, S.L., (2008). On the solution of certain kinetic equations, Applied Mathematics and Computation, 199, 504-511. |
| [47] | Saxena, R.K., Kalla, S.L. and Kiryakova, V.S., (2003). Relations connecting multi-index Mittag-Leffler functions and Riemann-Liouville fractional calculus, Algebras, Groups and Geometries, 20, 363-385. |
| [48] | Saxena, R.K., Mathai, A.M. and Haubold, H.J., (2002). On fractional kinetic equations, Astrophysics and Space Science, 282, 281-287. |
| [49] | Saxena, R.K. Mathai, A.M. and Haubold, H.J., (2004). On generalized fractional kinetic equations, Physica A, 344, 657-664. |
| [50] | Saxena, R.K., Mathai, A.M. and Haubold, H.J., (2004a). Unified fractional kinetic equations and a fractional diffusion equation, Astrophysics and Space Science, 290, 241-245. |
| [51] | Saxena, R.K., Mathai, A.M. and Haubold, H.J., (2004b). Astrophysical thermonuclear functions for Boltzmann-Gibbs statistics and Tsallis statistics, Physica A, 344, 649-656. |
| [52] | Saxena, R.K., Mathai, A.M. and Haubold, H.J., (2006). Fractional reaction-diffusion equations, Astrophysics and Space Science, 305, 289-296. |
| [53] | Saxena, R.K., Ram, C. and Kalla, S.L., (2002). Applications of generalized H-function in bivariate distributions, Rev. Acad. Canar., 14(1-2), 111-120. |
| [54] | Saxena, R.K. and Saigo, M., (2005). Certain properties of fractional calculus operators associated with generalized Wright function, Fractional Calculus and Applied Analysis, 6, 141-154. |
| [55] | Shampine,L. F., Robert Ketzscher,(March 2005). Using AD to solve BVPs in MATLAB Journal ACM Transactions on Mathematical Software, Volume 31 Issue 1, ACM New York, NY, USA. |
| [56] | Shukla, A. K. and Prajapati J. C., (2007). On some properties of a class of Polynomials suggested by Mittal, Proyecciones J. Math., 26(2), 145-156. |
| [57] | Shrivastava, P. N., (1974). Some operational formulas and generalized generating function, The Math. Education, 8, 19-22. |
| [58] | Singh, R. P., (1968). On generalized Truesdell polynomials, Rivista de Mathematica, 8, 345-353. |
| [59] | Srivastava, H. M. and Singhal, J. P., (1971). A class of polynomials defined by generalized |
| [60] | Rodrigues formula, Ann. Mat. Pura Appl., 90(4), 75-85. |
| [61] | Srivastava, H.M. and Saxena, R.K., (2001). Operators of fractional integration and their applications, Applied Mathematics and Computation, 118, 1-52. |
| [62] | Srivastava, A. N. and Singh, S. N., (1979). Some generating relations connected with a function |
| [63] | defined by a Generalized Rodrigues formula, Indian J. Pure Appl. Math., 10(10), 1312-1317. |
| [64] | Stephen, M. Watt, (2006). Making Computer Algebra More Symbolic (Invited), pp. 43-49, Proc. Transgressive Computing: A conference in honor or Jean Della Dora, (TC 2006), April 24-26 2006, Granada Spain. |
| [65] | Wiman, A., (1905). Über den Fundamental satz in der Theorie der Funcktionen, 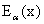 , Acta Mathematica, 29, 191-201. , Acta Mathematica, 29, 191-201. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML