-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(1): 62-66
doi:10.5923/j.ajms.20130301.09
Categories in Digital Images
Simge Öztunç , Ali Mutlu
Celal Bayar University , Faculty of Science and Arts, Department of Mathematics, Muradiye Campus, 45047, Manisa, Turkey
Correspondence to: Simge Öztunç , Celal Bayar University , Faculty of Science and Arts, Department of Mathematics, Muradiye Campus, 45047, Manisa, Turkey.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we recall some properties in digital topology for example, digital set, digital function, digital homotopy etc. from Boxer[5] and then give the definition of digital category. Also we present digital version of important category models.
Keywords: Digital Image, Digital Continuous Maps, Digital Homotopy, Digital Path, Digital Category
Cite this paper: Simge Öztunç , Ali Mutlu , Categories in Digital Images, American Journal of Mathematics and Statistics, Vol. 3 No. 1, 2013, pp. 62-66. doi: 10.5923/j.ajms.20130301.09.
1. Introduction
- Digital Topology is a branch of mathematics where the image processing and digital image processing is studied. Many Mathematicians, for example Rosenfeld, Kopperman, Han, Kong, Malgouyres, Boxer, Ayala, Karaca and others have contributed this area with their research. The notion of digital image, digital continuous map and digital homotopy studied in[3, 4, 6, 7, 12, 16]. Their recognition and efficient computation became a useful material for our study. Then we carry this notion to category theory and we construct some fundamental category models in digital topology. In section two we recall some definitions and properties from Boxer[5] in section three we introduce the ‘Digital Category’ and give basic examples of digital categories in order to construct a tool for category theory researchers.
2. Preliminaries
- In this paper we denote the set of integers by
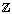 . Then
. Then 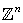 represents the set of lattice points in Euclidean
represents the set of lattice points in Euclidean 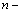 dimensional spaces. A finite subset of
dimensional spaces. A finite subset of 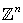 is called to be digital image.We will use a variety of adjacency relations it the digital image research. The following[7] are commonly used. Two points
is called to be digital image.We will use a variety of adjacency relations it the digital image research. The following[7] are commonly used. Two points 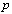 and
and 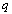 in
in 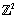 are
are 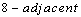 if they are distinct and differ by at most
if they are distinct and differ by at most 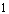 in each coordinate;
in each coordinate; 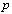 and
and 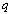 in
in 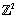 are
are 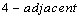 if they are
if they are 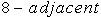 and differ in exactly one coordinate. Two points
and differ in exactly one coordinate. Two points 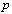 and
and 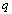 in
in 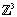 are
are 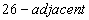 if they are distinct and differ by at most
if they are distinct and differ by at most 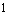 in each coordinate; they are
in each coordinate; they are  if they are
if they are 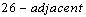 and differ in at most two coordinates; they are
and differ in at most two coordinates; they are 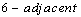 if they are
if they are 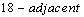 and differ in exactly one coordinate. For
and differ in exactly one coordinate. For 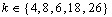 , a
, a 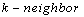 of a lattice point
of a lattice point 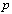 is a point that is
is a point that is 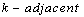 to
to 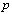 . We generalize
. We generalize 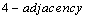 in
in 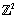 and
and 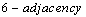 in
in 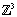 by taking
by taking 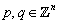 are
are 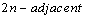 if
if 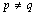 and
and 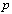 and
and 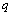 differ by
differ by 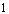 in one coordinate and by
in one coordinate and by 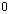 in all other coordinates.More extensive adjacency relations are investigated in[5]. In the following, if
in all other coordinates.More extensive adjacency relations are investigated in[5]. In the following, if 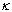 is an adjacency relation defined for an integer
is an adjacency relation defined for an integer 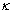 on
on 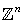 as one of the
as one of the 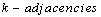 discussed above, that is, if
discussed above, that is, if or
or 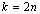 .We assume
.We assume 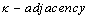 as
as 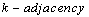 ,
, 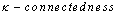 as
as 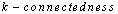 ,etc.Suppose that
,etc.Suppose that 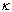 be an
be an 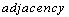 relation defined on
relation defined on 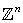 . A digital image
. A digital image 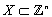 is
is 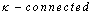 [5] if and only if for every pair of points
[5] if and only if for every pair of points 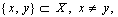 there is a set
there is a set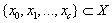 such that
such that 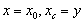 and
and 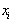 and
and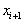 are
are 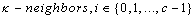 .Definition 2.1. Let
.Definition 2.1. Let 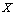 and
and 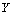 are digital images such that
are digital images such that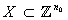 ,
, 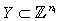 . Then the digital function
. Then the digital function 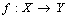 is a function which is defined between digital images.Definition 2.2. ([3]; see also[15]) Let
is a function which is defined between digital images.Definition 2.2. ([3]; see also[15]) Let 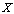 and
and 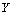 are digital images such that
are digital images such that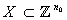 ,
, 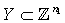 . Assume that
. Assume that 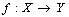 be a function. Let
be a function. Let 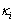 be an
be an 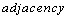 relation defined on
relation defined on 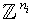 ,
, 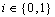 .
. 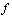 is called to be
is called to be 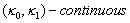 if the image under
if the image under 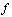 of every
of every 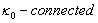 subset of
subset of 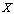 is
is 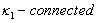 .A function satisfying Definition 2.1 is referred to be digitally continuous. A consequence of this definition is given below.Definition 2.3. ([3]; see also[15]) Let and are digital images. Then the function
.A function satisfying Definition 2.1 is referred to be digitally continuous. A consequence of this definition is given below.Definition 2.3. ([3]; see also[15]) Let and are digital images. Then the function 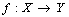 is said to be
is said to be 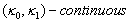 if and only if for every
if and only if for every 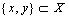 such that
such that 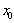 and
and 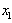 are
are 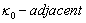 , either
, either 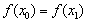 or
or 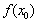 and
and 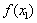 are
are 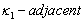 .Definition 2.4. ([2]) Let
.Definition 2.4. ([2]) Let 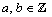 ,
, 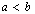 . A digital interval is a set of the form
. A digital interval is a set of the form 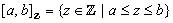 in which
in which 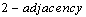 is assumed. For example, if
is assumed. For example, if 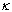 is an
is an 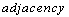 relation on a digital image
relation on a digital image 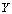 , then
, then 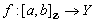 is
is 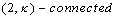 if and only if for every
if and only if for every 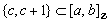 , either
, either 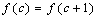 or
or 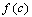 and
and 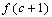 are
are 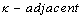 .Definition 2.5. ([3]; see also[6]) suppose that
.Definition 2.5. ([3]; see also[6]) suppose that 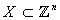 and
and 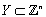 be digital images. Let
be digital images. Let 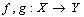 be
be 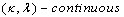 functions. Assume there is a positive integer
functions. Assume there is a positive integer 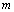 and a function
and a function 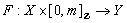 such thati) For all
such thati) For all 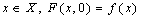 and
and 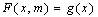 ;ii) For all
;ii) For all 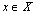 , the induced function
, the induced function 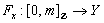 defined by
defined by 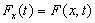 for all
for all 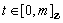 is
is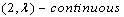 .iii) For all
.iii) For all 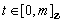 , the induced function
, the induced function 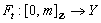 defined by
defined by 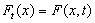 for all
for all 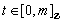 is
is 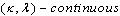 .Then
.Then 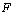 is called to be a digital
is called to be a digital 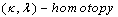 between
between 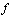 and
and 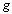 , and
, and 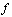 and
and 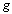 are said to be digitally
are said to be digitally 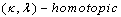 in
in 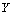 .We use the notation
.We use the notation 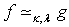 to denote
to denote 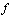 and
and 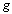 are digitally
are digitally 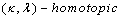 in
in 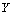 .Definition 2.6.[4]A digital
.Definition 2.6.[4]A digital 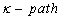 in a digital image is a
in a digital image is a  function
function 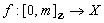 . Also if
. Also if 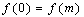 , we say that
, we say that 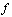 is a digital
is a digital 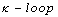 , and the point
, and the point 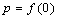 is the base point of the loop
is the base point of the loop 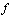 . If
. If 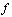 is a constant function, then it is called a trivial loop.If
is a constant function, then it is called a trivial loop.If 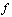 and
and 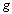 are digital
are digital 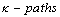 in
in 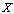 such that
such that 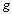 starts where
starts where 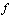 ends, the product of
ends, the product of 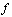 and
and 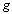 , written
, written 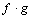 , is intuitively, the
, is intuitively, the 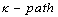 obtained by following
obtained by following 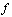 by
by 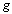 . Formally
. Formally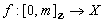 ,
,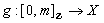 and
and 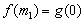 , then
, then 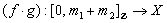 is defined by
is defined by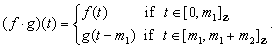 Definition 2.7. Let
Definition 2.7. Let 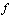 and
and 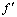 be
be 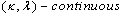 functions. Two paths
functions. Two paths 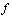 and
and 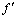 , mapping the digital interval
, mapping the digital interval 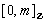 , are said to be digital path homotopic if they have the same initial point
, are said to be digital path homotopic if they have the same initial point 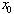 and the same final point
and the same final point 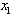 , and there is a
, and there is a 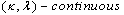 map
map 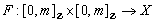 such that
such that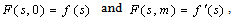
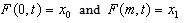 for each
for each 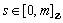 and each
and each 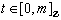 . We call to be a digital path homotopy between
. We call to be a digital path homotopy between 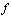 and
and 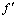 , and we write
, and we write 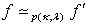 .
.3. Digital Categories
- Definition 3.1. A digital category is a quintuple
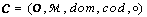 where (i)
where (i)  is a class whose members are called
is a class whose members are called 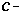 object. object are digital images.(ii)
object. object are digital images.(ii) 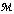 is a class whose members are called
is a class whose members are called 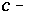 morphisms.
morphisms. 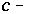 morphisms are digital functions which is defined between digital sets.(iii)
morphisms are digital functions which is defined between digital sets.(iii) 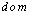 and
and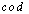 are digital functions from
are digital functions from 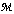 to (
to (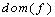 is called the domain of
is called the domain of 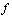 and
and 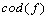 is called the codomain of
is called the codomain of 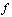 )(iv)
)(iv) 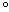 is a function from
is a function from 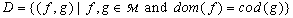 into
into 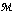 , called the composition law of
, called the composition law of 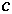 such that the following conditions are satisfied:(1) Matching Condition: If
such that the following conditions are satisfied:(1) Matching Condition: If 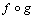 is defined, then
is defined, then 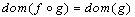 and
and 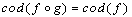 ;(2) Associativity Condition: If
;(2) Associativity Condition: If 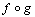 and
and 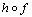 are defined, then
are defined, then 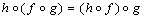 ;(3) Identity Existence Condition: For each
;(3) Identity Existence Condition: For each 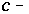 object
object 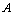 there exist
there exist 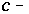 morphism
morphism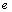 such that
such that 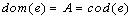 and (a)
and (a) 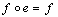 whenever
whenever 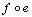 is defined, and(b)
is defined, and(b) 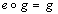 whenever
whenever 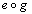 is defined;(4) Smallness of Morphism Class Condition: For any pair
is defined;(4) Smallness of Morphism Class Condition: For any pair 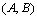 of
of 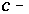 objects, the class
objects, the class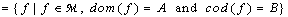 is a set.Let
is a set.Let 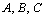 and
and 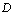 be digital images. We will use the notation
be digital images. We will use the notation 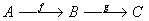 to denote the composition
to denote the composition 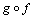 . Thus the statement that the triangle
. Thus the statement that the triangle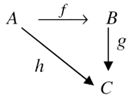 is equivalent to the statement that
is equivalent to the statement that 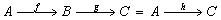 . When morphisms
. When morphisms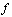 and
and 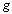 exist such that the above triangle commutes, we say that
exist such that the above triangle commutes, we say that 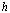 factor through
factor through 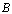 . Similarly the statement that the square
. Similarly the statement that the square 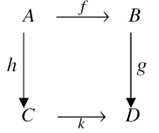 commutes means that
commutes means that 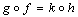 .Proposition 3.1. Let
.Proposition 3.1. Let 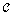 be a digital category and
be a digital category and  is a
is a 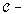 object such that
object such that 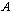 is a digital image. Then there exist exactly one
is a digital image. Then there exist exactly one 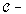 morphism
morphism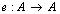 satisfiying the properties 3(a) and 3(b) of Definition 3.1; i.e. such that (a)
satisfiying the properties 3(a) and 3(b) of Definition 3.1; i.e. such that (a) 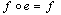 whenever
whenever 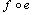 is defined, and(b)
is defined, and(b) 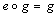 whenever
whenever 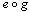 is defined;Proof: Suppose that each of
is defined;Proof: Suppose that each of 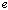 and
and 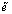 is such a morphism. Then by (a)
is such a morphism. Then by (a) 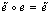 and by (b)
and by (b) 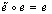 ; hence,
; hence, 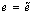 .Definition 3.2. For each object
.Definition 3.2. For each object 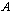 of the digital category
of the digital category 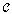 , the unique
, the unique 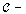 morphism
morphism 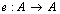 satishfiying (a) and (b) above is denoted by
satishfiying (a) and (b) above is denoted by 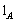 and is called the
and is called the 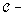 identity of
identity of 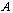 .Definition 3.3. A digital category
.Definition 3.3. A digital category 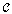 is said to be:(1) Small provided that
is said to be:(1) Small provided that 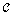 is a digital set;(2) Discrete provided that all of its morphisms are identities;(3) Connected that for each pair
is a digital set;(2) Discrete provided that all of its morphisms are identities;(3) Connected that for each pair 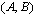 of
of 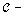 objects,
objects, 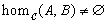 .
.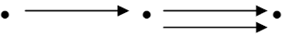 and
and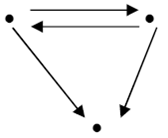 can be considered to be digital categories, but neither
can be considered to be digital categories, but neither nor
nor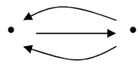 can be digital categories.Definition 3.4. For each natural number
can be digital categories.Definition 3.4. For each natural number 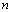 , the set
, the set 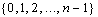 supplied with the usual order can be considered to be digital category
supplied with the usual order can be considered to be digital category 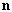 , thus we have the special small digital categories:
, thus we have the special small digital categories: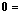 The empty category
The empty category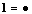
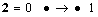
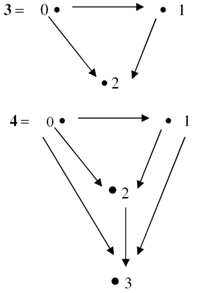 Boxer defined the path homotopy in [5]. We can consider equivalence classes of digital paths (path homotopy classes) because digital path homotopy relation is an equivalence relation.Example 3.2. Given a digital image
Boxer defined the path homotopy in [5]. We can consider equivalence classes of digital paths (path homotopy classes) because digital path homotopy relation is an equivalence relation.Example 3.2. Given a digital image  and points
and points 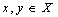 a digital
a digital 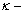 path from
path from 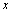 to
to 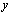 is a
is a 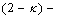 continuous mapping
continuous mapping 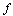 from some digital set
from some digital set  to
to 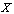 with
with 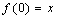 and
and 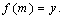 If
If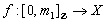 is a digital path from
is a digital path from 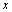 to
to 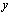 and
and 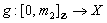 is a digital path from
is a digital path from 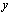 to
to 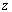 , there is a path
, there is a path 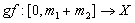 defined by
defined by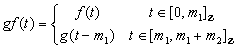 from
from 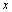 to
to 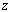 .This makes
.This makes 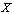 into a category, the digital path category of
into a category, the digital path category of 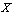 .Now given digital paths
.Now given digital paths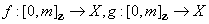 , both from
, both from 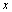 to
to 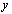 .There is a digital continuous mapping
.There is a digital continuous mapping 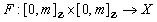 in a digital image in such that
in a digital image in such that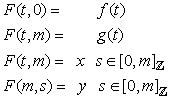 It easy to see that this is an equivalence relation. The quotient of the digital path category by this congruence relation is a category called the digital category of digital homotopy classes of digital paths in
It easy to see that this is an equivalence relation. The quotient of the digital path category by this congruence relation is a category called the digital category of digital homotopy classes of digital paths in 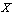 .Definition 3.5. Let
.Definition 3.5. Let 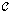 be a digital category and
be a digital category and 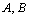 digital digital sets. A digital morphism
digital digital sets. A digital morphism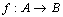 in
in 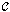 said to be monic if it is left cancelable.Theorem 3.1. Suppose that
said to be monic if it is left cancelable.Theorem 3.1. Suppose that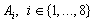 be digital sets. Consider the following ‘cube’ of digital objects and digital morphisms in a given digital category
be digital sets. Consider the following ‘cube’ of digital objects and digital morphisms in a given digital category 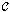 :
: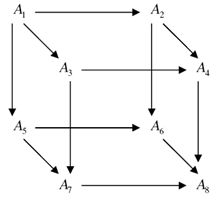 (i) Suppose that all faces except the top face are given to be commutative. If
(i) Suppose that all faces except the top face are given to be commutative. If 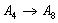 is monic, then the top face is also commutative.(ii) Suppose that all faces except the bottom face are given to be commutative. If
is monic, then the top face is also commutative.(ii) Suppose that all faces except the bottom face are given to be commutative. If 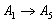 is epic, then the bottom face is also commutative.Proof: Let
is epic, then the bottom face is also commutative.Proof: Let 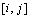 denote the digital morphism from
denote the digital morphism from 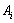 to
to 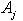 . We have to prove that
. We have to prove that 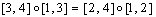 . Now
. Now 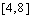 is given to be monic and (writing
is given to be monic and (writing  as juxtaposition)
as juxtaposition) 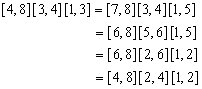 Then the result follows by left cancellation of
Then the result follows by left cancellation of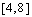 .ii) We have to prove that
.ii) We have to prove that 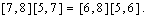 [1,5] is given to be epic and
[1,5] is given to be epic and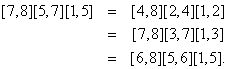 Then the result follows by right cancellation of
Then the result follows by right cancellation of  Example 3.3.Given a digital image
Example 3.3.Given a digital image 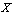 and points
and points 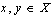 a digital
a digital 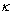 path from
path from 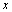 to
to 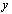 is a
is a 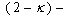 continuous mapping
continuous mapping 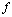 from some digital set
from some digital set 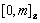 to
to 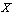 with
with 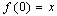 and
and 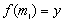 . If
. If 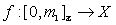 is a digital path from
is a digital path from 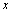 to
to 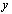 and
and 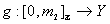 is a digital path from
is a digital path from 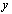 to
to there is a path
there is a path 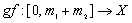 defined by
defined by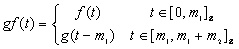 from
from 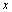 to
to  . This makes
. This makes 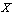 into a category the digital path category of
into a category the digital path category of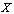 . Now given digital paths
. Now given digital paths 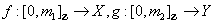 , both from
, both from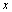 to
to 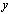 , one can define
, one can define 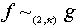 if there is a continuous map
if there is a continuous map 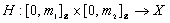
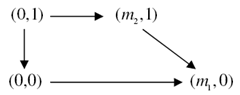 in
in 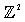 such that
such that 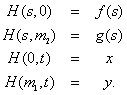
4. Conclusions
- In this paper we construct the digital category model for digital images and gave some conditions made the diagram commutative.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML