Keldibay Alymkulov
Department of Algebra and Geometry, Osh State University, Osh, 723504, Kyrgyzstan
Correspondence to: Keldibay Alymkulov , Department of Algebra and Geometry, Osh State University, Osh, 723504, Kyrgyzstan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The possibility of application of the boundary layer function for constructing the asymptotic solution of the singulary perturbed of Lighthill model equation in the case when corresponding not perturbed equation have the pole of the entire order on the regular singular point is proved. Earlier asymptotic of this problem was constructed by the method of uniformization and structural matching. The relations between the methods of the boundary layer function, uniformization and structural matching are analyzed.
Keywords:
Singulary Point, Singulary Perturbed Equation, Asymptotic Of Solution, Model Equation Of Lighthill, Method Of Boundary Layer Function (MBLF), Method Of Uniformization (MU), Method Of Structural Matching (MSM)
Cite this paper: Keldibay Alymkulov , Analog of the Method of Boundary Layer Function for the Solution of the Lighthill’s Model Equation with the Regular Singular Point, American Journal of Mathematics and Statistics, Vol. 3 No. 1, 2013, pp. 53-61. doi: 10.5923/j.ajms.20130301.08.
1. Introduction
Famous English mechanic and mathematician J. M. Lighthill in[1] studied the following problem of the perturbed ordinary differential equation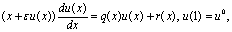 | (1) |
where 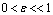 - small parameter ,
- small parameter , 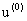 - is given date,
- is given date, 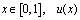 - unknown function ,
- unknown function , 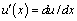 ,
,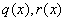 - analytical functions on the interval
- analytical functions on the interval 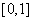 .He used the idea of Poincare method in the theory nonlinear oscillations propose to seek of asymptotic of the solution of this problem in the form
.He used the idea of Poincare method in the theory nonlinear oscillations propose to seek of asymptotic of the solution of this problem in the form 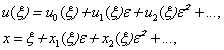 | (2) |
and here are not the rule to determine unknown functions 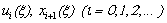 .This approach was named after him as the method of Lighthill. Point x=0 is singular point for unperturbed equation (1)
.This approach was named after him as the method of Lighthill. Point x=0 is singular point for unperturbed equation (1) 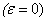
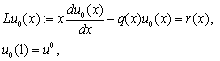 | (3) |
We will set that 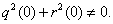 We note that the solution of the problem (3) has the view:
We note that the solution of the problem (3) has the view: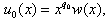 | (4) |
here 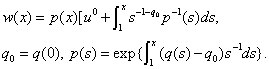 If
If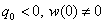 , then the solution (4) unbounded function on the interval
, then the solution (4) unbounded function on the interval 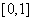 and the point
and the point 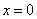 is the pole of (4).The method of Lighthill developed by G. F. Carrier , W. A. Wasow , H. S. Tsien , G. Temple, M. F. Pritulo, Sibuya and K. J. Tahahasy, H. J. Hoogstraten, C. Comstok, P. Habets, K. Alymkulov and others. It is possible to read these historical reviews in[2-5].Lighthill’s method was simplified in[4-5]. The equivalence of the problem (1) to the following uniformization problem is proved here
is the pole of (4).The method of Lighthill developed by G. F. Carrier , W. A. Wasow , H. S. Tsien , G. Temple, M. F. Pritulo, Sibuya and K. J. Tahahasy, H. J. Hoogstraten, C. Comstok, P. Habets, K. Alymkulov and others. It is possible to read these historical reviews in[2-5].Lighthill’s method was simplified in[4-5]. The equivalence of the problem (1) to the following uniformization problem is proved here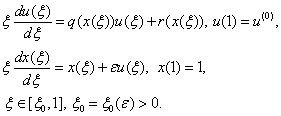 | (5) |
Now we can seek the solution of the problem (1) in the view (2). This method was called the method of uniformization (MU) by suggestion of J. Temple[6], since he solved an example by this method.It is proved the following Theorem in[4].Theorem. Let 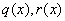 - analytical functions on the interval
- analytical functions on the interval 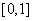 . If
. If 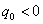 and
and 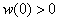 then the solution of the problem (1) exist on the interval
then the solution of the problem (1) exist on the interval 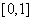 and his asymptotic will have the presentation in the parametric view (4).The comment of this theorem: a) Here it is not the condition of Wasov[7]:
and his asymptotic will have the presentation in the parametric view (4).The comment of this theorem: a) Here it is not the condition of Wasov[7]: 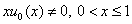 ,b) It is sufficient for existence of the solution problem (1) it is necessary to know the solution unperturbed equation and to check conditions:
,b) It is sufficient for existence of the solution problem (1) it is necessary to know the solution unperturbed equation and to check conditions: 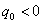 ,
,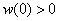 .In[8-9] the asymptotic of the solution this problem was received by the method of structural matching. Here the solution of Lighthill’s model equation is constructed by the boundary layer function[12-18] in the case when corresponding not perturbed equation has the pole of the entire order on the regular singular point. In[17] considered the case when corresponding not perturbed equation has the pole of the order one on the regular singular point and the solution constructed by the method of boundary layer function. But method of the proof in[17] is not suitable in the case when the order of pole is more than one (see below the beginning of the proof of the Theorem 1).Usually the method of boundary layer function (MBLF) is applied for constructing the asymptotic solution of the singular perturbed equations with small parameter at higher derivatives; many articles and books are written to elaborate this method[12-18] .Now we will say a few words about MSM. MSM is a simplified version of the method of Van Dike and it was created in 2000-2002. We can apply this method for constructing asymptotic singulary perturbed equations with a small parameter at higher derivative (that is equations Prandtle-Tihonov types)[10-11] as singulary perturbed equations type of Lighthill[8-9].
.In[8-9] the asymptotic of the solution this problem was received by the method of structural matching. Here the solution of Lighthill’s model equation is constructed by the boundary layer function[12-18] in the case when corresponding not perturbed equation has the pole of the entire order on the regular singular point. In[17] considered the case when corresponding not perturbed equation has the pole of the order one on the regular singular point and the solution constructed by the method of boundary layer function. But method of the proof in[17] is not suitable in the case when the order of pole is more than one (see below the beginning of the proof of the Theorem 1).Usually the method of boundary layer function (MBLF) is applied for constructing the asymptotic solution of the singular perturbed equations with small parameter at higher derivatives; many articles and books are written to elaborate this method[12-18] .Now we will say a few words about MSM. MSM is a simplified version of the method of Van Dike and it was created in 2000-2002. We can apply this method for constructing asymptotic singulary perturbed equations with a small parameter at higher derivative (that is equations Prandtle-Tihonov types)[10-11] as singulary perturbed equations type of Lighthill[8-9].
2. Statement of the Problem
Here we will consider the case when 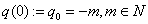 , for simplicity. Therefore the solution (4) of the unperturbed equation (3) we can rewrite in the view
, for simplicity. Therefore the solution (4) of the unperturbed equation (3) we can rewrite in the view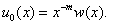 | (6) |
And this solution will have the pole of order 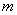 , when
, when 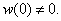 To given functions we will impose the following conditions
To given functions we will impose the following conditions
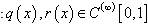 . We must prove the condition of existing of the solution of the problem (1) and construct asymptotic of this one.
. We must prove the condition of existing of the solution of the problem (1) and construct asymptotic of this one.
3. Constructing the Solution of This Problem by the Method of the Boundary Layer Function
The solution of the problem (1) we will seek in the form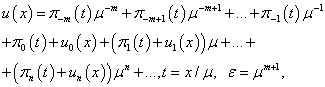 | (7) |
here 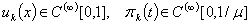 . We denote, that function
. We denote, that function 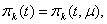 .e.
.e. 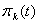 will depend from
will depend from 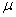 , but this dependent not pointed for brevity.Initial data for functions
, but this dependent not pointed for brevity.Initial data for functions 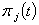 we will take in the form:
we will take in the form: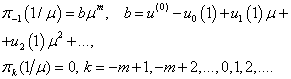 Substituting (3) on (1) we will have for define of functions
Substituting (3) on (1) we will have for define of functions 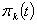
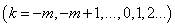 , and
, and 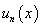
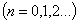 we have the following equations:
we have the following equations: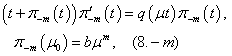
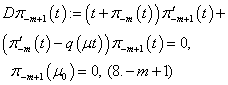
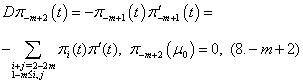
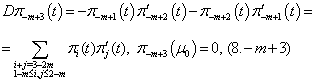
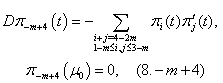
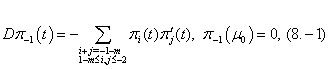
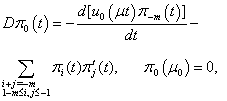 | (8.0) |
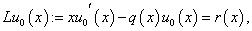 | (9.0) |
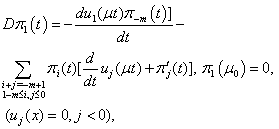 | (8.1) |
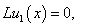 | (9.1) |
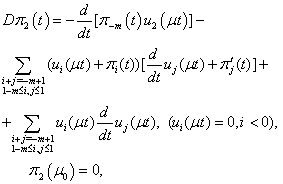 | (8.2) |
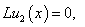 | (9.2) |
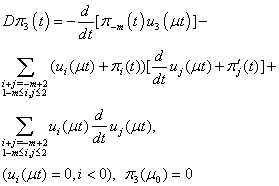 | (8.3) |
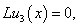 | (9.3) |
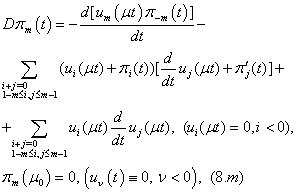
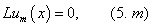
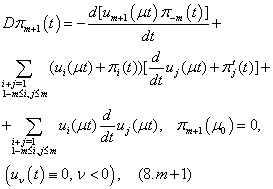
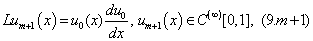
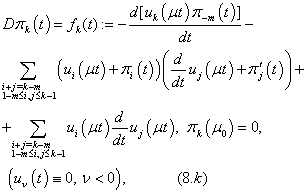
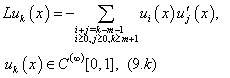 Now we will solve these problems consecutively. We are to prove the existence of the solution of equations (5.0), (5.1), (5.2) that need the following lemma.Lemma 1. The equation
Now we will solve these problems consecutively. We are to prove the existence of the solution of equations (5.0), (5.1), (5.2) that need the following lemma.Lemma 1. The equation 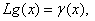 | (10) |
here 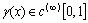 have unique bounded solution from
have unique bounded solution from 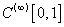 and his have the following view
and his have the following view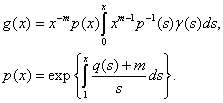 | (11) |
Really, general solution of the equation (16) has the view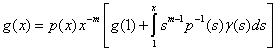 .If we set
.If we set 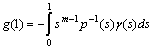 , then we have got (11).From this Lemma follow that equations (9.0), (9.1),… will have unique solutions and
, then we have got (11).From this Lemma follow that equations (9.0), (9.1),… will have unique solutions and 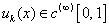
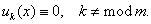 .Theorem 1. If it is hold:
.Theorem 1. If it is hold: 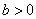 then the problem (8.-m) have unique bounded positive solution in
then the problem (8.-m) have unique bounded positive solution in 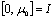 and
and 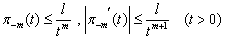 .Here and further we will denote by
.Here and further we will denote by 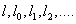 constants, which are do not depend from
constants, which are do not depend from 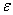 .Proof. In order to proof of existing of the solution of this equation in[17] was applied the following approach. We will rewrite (8.-m) as equation
.Proof. In order to proof of existing of the solution of this equation in[17] was applied the following approach. We will rewrite (8.-m) as equation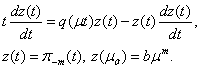 By solving this equation as inhomogeneous equation we have got
By solving this equation as inhomogeneous equation we have got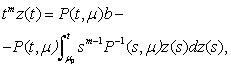 | (12) |
here 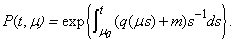 If
If 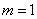 after integrating by parts the equation (12) will reduce to
after integrating by parts the equation (12) will reduce to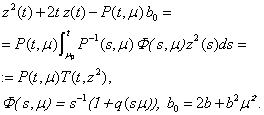 | (13) |
Let 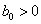 , then by solving this equation as quadratic equation we have got
, then by solving this equation as quadratic equation we have got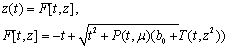 It is proved[17] that this equation will have a unique solution In the class
It is proved[17] that this equation will have a unique solution In the class 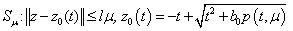 ,
,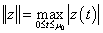 .It is impossible to apply such an approach when
.It is impossible to apply such an approach when 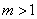 .Really in this case the equation (13) will have the following view:
.Really in this case the equation (13) will have the following view: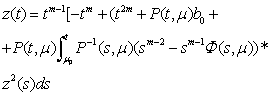 Since
Since 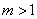 it is singular integral equation and we can not to solve the previous approach.Now we will to solve the equation (8.-m) by method of variation constant of Lagrange. This equation we will rewrite in the form of
it is singular integral equation and we can not to solve the previous approach.Now we will to solve the equation (8.-m) by method of variation constant of Lagrange. This equation we will rewrite in the form of 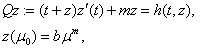 | (14) |
here 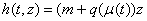 .The problem
.The problem 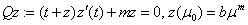 will have the following solution
will have the following solution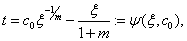 | (15) |
where 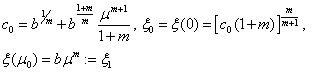 .Thus,
.Thus, 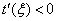 ,
, 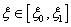 , therefore exists a unique bounded positive strictly decreasing solution
, therefore exists a unique bounded positive strictly decreasing solution 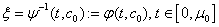 From (15) we have
From (15) we have 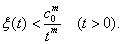 | (16) |
The solution of the problem (14) we will seek by the method of variation parameters of Lagrange 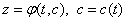 .Then for
.Then for 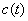 we have the following equation
we have the following equation 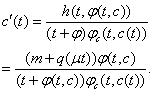 | (17) |
From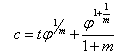 follow
follow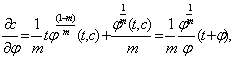 | (18) |
Therefore we can (17) rewrite in the following view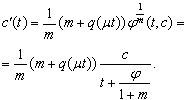 From here we have got
From here we have got 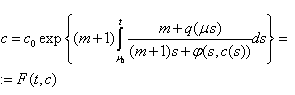 It is evident, that the function
It is evident, that the function 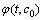 maps
maps 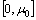 to
to 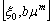 .Operator
.Operator 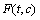 maps the segment
maps the segment 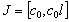 to itself. Using
to itself. Using 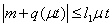 , we have got
, we have got 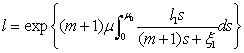 . Now we will proof, that operator F is contracting in J. Since
. Now we will proof, that operator F is contracting in J. Since 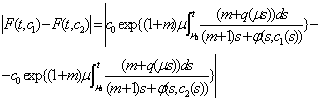 From here applying mean value theorem of Lagrange, we have got
From here applying mean value theorem of Lagrange, we have got 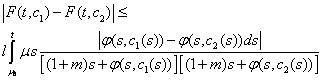 By using (18) we have
By using (18) we have 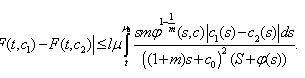 From here by divide this integral to two and by using (16) we have got
From here by divide this integral to two and by using (16) we have got 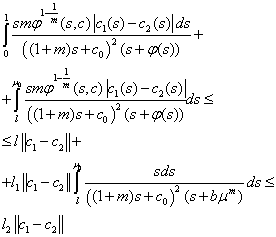 Therefore
Therefore 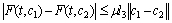 .It is shown, that operator F contracting on J. Now we will solve the problems (4.m+k) (k=1, 2, …). For solving this problem we will use the following: Lemma 2. The equation
.It is shown, that operator F contracting on J. Now we will solve the problems (4.m+k) (k=1, 2, …). For solving this problem we will use the following: Lemma 2. The equation 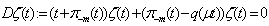 has the a fundamental solution
has the a fundamental solution 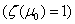
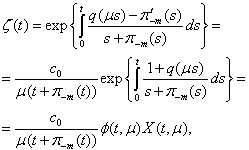 here
here 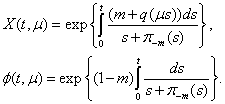 ,.It is evident from terms
,.It is evident from terms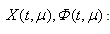
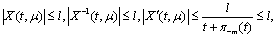
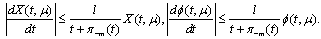 Lemma 3. The inhomogeneous equation (8.k)
Lemma 3. The inhomogeneous equation (8.k)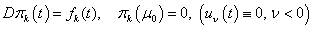 will have the unique solution and
will have the unique solution and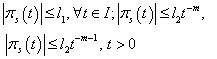 We will prove this lemma for the case
We will prove this lemma for the case 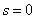 , other cases are proved analogously.(4.-m+1) is homogeneous equation with zero origin conditions, therefore:
, other cases are proved analogously.(4.-m+1) is homogeneous equation with zero origin conditions, therefore: 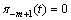 . Analogously:
. Analogously: 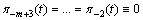 . We have for
. We have for 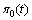 the following problem
the following problem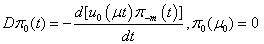 | (19) |
The solution of the equation of (19) will represent of the view: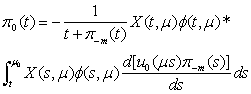 After integrating by parts we have
After integrating by parts we have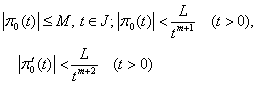 | (20) |
The case 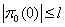 will prove analogously by dividing integrals into two from
will prove analogously by dividing integrals into two from 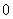 two 1 and from 1 to
two 1 and from 1 to 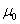 .Therefore we proved the following: Lemma 2. The problem (19) has a unique bounded solution in
.Therefore we proved the following: Lemma 2. The problem (19) has a unique bounded solution in 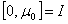 and it is valid for evaluations (20). Analogously equations (8.к) (к=1, 2, …) have unique bounded solutions in
and it is valid for evaluations (20). Analogously equations (8.к) (к=1, 2, …) have unique bounded solutions in 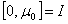 from
from 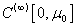 and
and 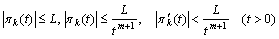 .We proved the following: Theorem 2. Let’s fulfilled condition
.We proved the following: Theorem 2. Let’s fulfilled condition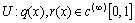 ,
, 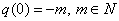 ,
, 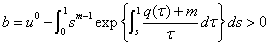 . The solution of the problem (1) will have unique solution and his asymptotic represent in the view (3) and
. The solution of the problem (1) will have unique solution and his asymptotic represent in the view (3) and 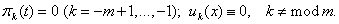
4. The Estimate of the Remainder Term of Series (4)
Now we will proof the estimate of the remainder term, that is, the series (4) really is asymptotic series.Lemma 3. Let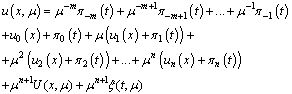 | (21) |
then 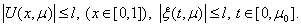 We will prove this lemma for brevity for
We will prove this lemma for brevity for 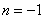 , that is
, that is 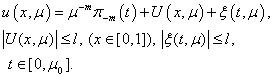 | (22) |
Proof. After substitute (22) into (2) for 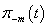 we have the equation (8.-m), for
we have the equation (8.-m), for 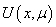 and
and 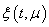 we have got:
we have got: 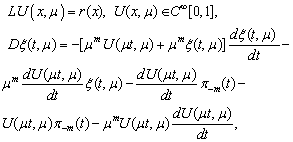 | (23) |
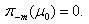 | (24) |
The equation (23) has the solution 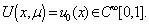 It is from (24) we will go to the integral equation
It is from (24) we will go to the integral equation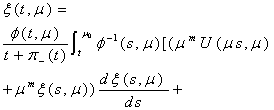
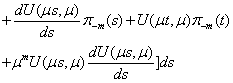 .After integrate by parts the second term we have the weekly perturbed integral equation of Volterra that will have unique bounded solution in
.After integrate by parts the second term we have the weekly perturbed integral equation of Volterra that will have unique bounded solution in 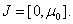 Lemma 3 is proved.
Lemma 3 is proved.
5. The Example Comparison of Three Methods: Method of Boundary Layer Functions, Method of Uniformization and Method of Structural Matching
It is considered a problem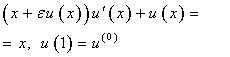 | (25) |
This equation has the exact solution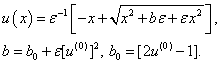 | (26) |
If 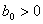 , then (26) exist on interval
, then (26) exist on interval 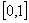 and
and 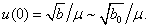 | (27) |
I. At first we will construct the solution of the problem (25) by method of boundary layer functions, that is 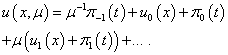 | (28) |
Initial data for functions 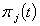 we will take in the form:
we will take in the form: 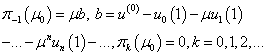 Then for functions
Then for functions 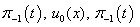 we have the following problems
we have the following problems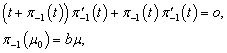
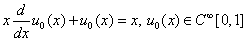 ,
,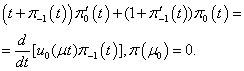 From here we have got
From here we have got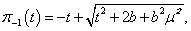
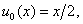
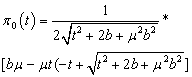 .Therefore we will rewrite (28) in the form
.Therefore we will rewrite (28) in the form 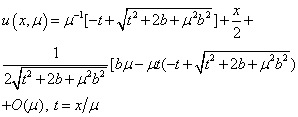 | (29) |
Let 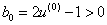 . Since
. Since 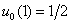 , then
, then 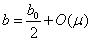 . If we set
. If we set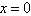 into (29), then
into (29), then 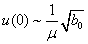 . It will agree with (27).II. We will construct of the solution of the problem (25) by the method of structural matching
. It will agree with (27).II. We will construct of the solution of the problem (25) by the method of structural matching . It is considered instead of (25) the following uniformization equation (see (5))
. It is considered instead of (25) the following uniformization equation (see (5))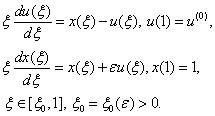 | (30) |
solution of this equation is represented in the form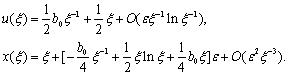 | (31) |
From second equality, after solving the equation 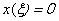 we have got
we have got 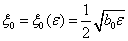 .If we set this meaning to the first equality (31), then
.If we set this meaning to the first equality (31), then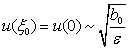 ,That will agree with (27) too.III. Now we will construct the solution of the problem (25) by the method of structural matching[8-11]. a) Firstly we will construct the outer solution (
,That will agree with (27) too.III. Now we will construct the solution of the problem (25) by the method of structural matching[8-11]. a) Firstly we will construct the outer solution (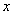 -outer variable and not depend from ) of this problem with the initial condition
-outer variable and not depend from ) of this problem with the initial condition 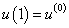 . We will have
. We will have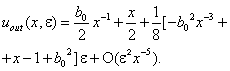 | (32) |
That is hold in the interval 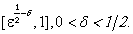 b) Secondly we will construct the inner solution of the problem (25), that satisfy this equation of the singular point
b) Secondly we will construct the inner solution of the problem (25), that satisfy this equation of the singular point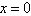 near. For this introduce inner variable
near. For this introduce inner variable 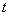 by formula:
by formula: 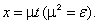 Then equation (25) we will rewrite in the form
Then equation (25) we will rewrite in the form 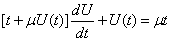 | (33) |
The solution of this equation has the view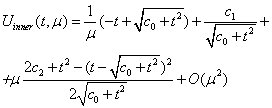 | (34) |
here 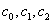 - arbitrary constants. If the outer solution (32) we will rewrite in the inner variable
- arbitrary constants. If the outer solution (32) we will rewrite in the inner variable 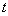 , then
, then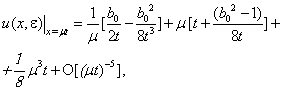 | (35) |
If we will select constants 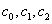 such
such 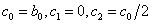 , then the outer solution and inner solution agree and the inner solution will have the form
, then the outer solution and inner solution agree and the inner solution will have the form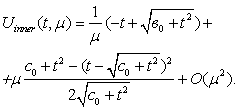 | (36) |
Now the uniform solution of the problem (25) will have the following form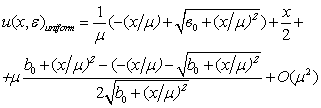 If we will set here
If we will set here 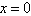 , then
, then 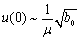 , this agrees with (27).
, this agrees with (27).
6. Conclusions
From this example it can be seen that the method of boundary layer function is at labour-intensive than the method of uniformization and the method of structural matching. But the method of structural matching we can apply to construct asymptotic solution of to almost all singularly perturbed equations.
ACKNOWLEDGMENTS
I sincerely thank the unknown to me reviewer for his benevolent review of my article.
References
| [1] | M. G. Lighthill, A technique for rendering approximate solution to physical problems uniformly valid. Phil. Mag., 40 (1949), 1179-1201. |
| [2] | H. S. Tsien. The Poincare-Lighthill-Kuo Method. Adv. Apll. Math., v. 4, 1956, pp. 281-349. |
| [3] | C. Comstok. The Poincare-Lighthill perturbation technique and its generalizations. SIAM Review, Vol. 14, No.3, 1972. |
| [4] | К. Аlymkulov, Method of uniformization and the validity of the Lighthill method, Izvestia of Academy Science. Kyrgyz SSR (in Russian), 1981, No.1, pp. 35-38. |
| [5] | К. Аlymkulov. Perturbed differential equations with singular points and some problems of bifurcations tasks (in Russian), Bishkek, Ilim, 1992. |
| [6] | G. Temple. Linearization and delinearization. Proc. Math. Congress, Edinburgh, 1958, pp. 233-247. |
| [7] | W. A. Wasov. On the convergence of an approximation method of M. J. Lighthill. J. Rational Mech. Anal., Vol. 4, 1955, pp. 751-767. |
| [8] | K. Alymkulov, Jeentaeva J. K. Method of structural matching the solution to the Lighthill model equation with a regular singular point. Reports. Maths, Vol. 70, No2, 2004, p. 1-6. |
| [9] | K. Alymkulov, J. K. Jeentaeva. Method of structural matching of the model of Lighthill equation with the regular critical point. Math. Notes, Vol. 79, No. 5, 2006, 643-652. |
| [10] | Alymkulov K., Zulpukarov A. Z. Uniform asymptotic of the solution of the boundary - value problem of the singularly perturbed equation with weak singular point (in Russian). Reports of Russian Academy of Sciences, Vol. 398, No.5, 2004, pp. 1-4. |
| [11] | A. Z. Zulpukarov. Method of structural matching of solutions boundary value problem of singulary perturbed equation with singular points (in Russian). Author's abstract of dissertation, Osh, 2009. |
| [12] | A. B. Vasil'eva, V. F. Butuzov. Asymptotical expansions of the solution of singulary perturbed equations (in Russian), Moscow, Nauka, 1973. |
| [13] | A. B. Vasil'eva, V. F. Butuzov, L. V. Kalachev. The Boundary Function Method for Singular Perturbed Problems, SIAM (Cambridge University Press), 1987. |
| [14] | M. I. Imanaliev. Asymptotical Methods in the Theory of Singulary Perturbed Integro-Differential Systems (in Russian), Bishkek, Ilim, 1972. |
| [15] | V. A. Trenogin, Development and application of the asymptotical Lusternik-Vishik method, Russian Math. Surveys, 25:4 (1970), 119-156. |
| [16] | O’Malley R. E., Singular Perturbation Methods for Ordinary Differential Equations, Springer-Verlag, 1991. |
| [17] | К. Аlymkulov, A. Khalmatov. Boundary Function Method for solving the model Lighthill Equation with a Regular Singular Point. Mathem. Notes, Vol. 92, No.6, 2012, pp. 751-755 (Transl. from Mathematicheskie zametki, 2012, Vol.92, No. 6 pp. 819-824). |
| [18] | К.Аlymkulov, T. D Asylbekov, S. F. Dolbeeva. Generalization of the boundary function method for the boundary problem of the bisingulary perturbed differential equation (in Russian). Mathematicheskie zametki, 2013, in print). |

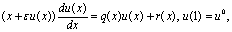
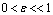 - small parameter ,
- small parameter , 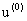 - is given date,
- is given date, 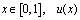 - unknown function ,
- unknown function , 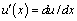 ,
,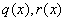 - analytical functions on the interval
- analytical functions on the interval 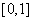 .He used the idea of Poincare method in the theory nonlinear oscillations propose to seek of asymptotic of the solution of this problem in the form
.He used the idea of Poincare method in the theory nonlinear oscillations propose to seek of asymptotic of the solution of this problem in the form 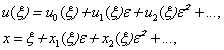
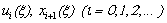 .This approach was named after him as the method of Lighthill. Point x=0 is singular point for unperturbed equation (1)
.This approach was named after him as the method of Lighthill. Point x=0 is singular point for unperturbed equation (1) 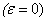
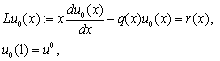
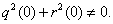 We note that the solution of the problem (3) has the view:
We note that the solution of the problem (3) has the view: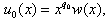
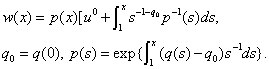 If
If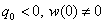 , then the solution (4) unbounded function on the interval
, then the solution (4) unbounded function on the interval 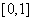 and the point
and the point 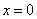 is the pole of (4).The method of Lighthill developed by G. F. Carrier , W. A. Wasow , H. S. Tsien , G. Temple, M. F. Pritulo, Sibuya and K. J. Tahahasy, H. J. Hoogstraten, C. Comstok, P. Habets, K. Alymkulov and others. It is possible to read these historical reviews in[2-5].Lighthill’s method was simplified in[4-5]. The equivalence of the problem (1) to the following uniformization problem is proved here
is the pole of (4).The method of Lighthill developed by G. F. Carrier , W. A. Wasow , H. S. Tsien , G. Temple, M. F. Pritulo, Sibuya and K. J. Tahahasy, H. J. Hoogstraten, C. Comstok, P. Habets, K. Alymkulov and others. It is possible to read these historical reviews in[2-5].Lighthill’s method was simplified in[4-5]. The equivalence of the problem (1) to the following uniformization problem is proved here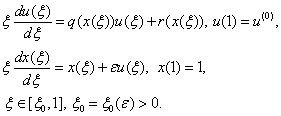
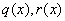 - analytical functions on the interval
- analytical functions on the interval 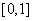 . If
. If 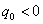 and
and 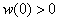 then the solution of the problem (1) exist on the interval
then the solution of the problem (1) exist on the interval 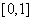 and his asymptotic will have the presentation in the parametric view (4).The comment of this theorem: a) Here it is not the condition of Wasov[7]:
and his asymptotic will have the presentation in the parametric view (4).The comment of this theorem: a) Here it is not the condition of Wasov[7]: 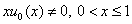 ,b) It is sufficient for existence of the solution problem (1) it is necessary to know the solution unperturbed equation and to check conditions:
,b) It is sufficient for existence of the solution problem (1) it is necessary to know the solution unperturbed equation and to check conditions: 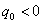 ,
,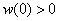 .In[8-9] the asymptotic of the solution this problem was received by the method of structural matching. Here the solution of Lighthill’s model equation is constructed by the boundary layer function[12-18] in the case when corresponding not perturbed equation has the pole of the entire order on the regular singular point. In[17] considered the case when corresponding not perturbed equation has the pole of the order one on the regular singular point and the solution constructed by the method of boundary layer function. But method of the proof in[17] is not suitable in the case when the order of pole is more than one (see below the beginning of the proof of the Theorem 1).Usually the method of boundary layer function (MBLF) is applied for constructing the asymptotic solution of the singular perturbed equations with small parameter at higher derivatives; many articles and books are written to elaborate this method[12-18] .Now we will say a few words about MSM. MSM is a simplified version of the method of Van Dike and it was created in 2000-2002. We can apply this method for constructing asymptotic singulary perturbed equations with a small parameter at higher derivative (that is equations Prandtle-Tihonov types)[10-11] as singulary perturbed equations type of Lighthill[8-9].
.In[8-9] the asymptotic of the solution this problem was received by the method of structural matching. Here the solution of Lighthill’s model equation is constructed by the boundary layer function[12-18] in the case when corresponding not perturbed equation has the pole of the entire order on the regular singular point. In[17] considered the case when corresponding not perturbed equation has the pole of the order one on the regular singular point and the solution constructed by the method of boundary layer function. But method of the proof in[17] is not suitable in the case when the order of pole is more than one (see below the beginning of the proof of the Theorem 1).Usually the method of boundary layer function (MBLF) is applied for constructing the asymptotic solution of the singular perturbed equations with small parameter at higher derivatives; many articles and books are written to elaborate this method[12-18] .Now we will say a few words about MSM. MSM is a simplified version of the method of Van Dike and it was created in 2000-2002. We can apply this method for constructing asymptotic singulary perturbed equations with a small parameter at higher derivative (that is equations Prandtle-Tihonov types)[10-11] as singulary perturbed equations type of Lighthill[8-9].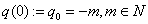 , for simplicity. Therefore the solution (4) of the unperturbed equation (3) we can rewrite in the view
, for simplicity. Therefore the solution (4) of the unperturbed equation (3) we can rewrite in the view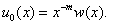
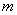 , when
, when 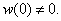 To given functions we will impose the following conditions
To given functions we will impose the following conditions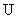
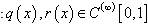 . We must prove the condition of existing of the solution of the problem (1) and construct asymptotic of this one.
. We must prove the condition of existing of the solution of the problem (1) and construct asymptotic of this one.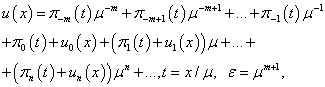
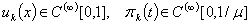 . We denote, that function
. We denote, that function 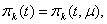 .e.
.e. 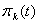 will depend from
will depend from 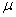 , but this dependent not pointed for brevity.Initial data for functions
, but this dependent not pointed for brevity.Initial data for functions 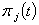 we will take in the form:
we will take in the form: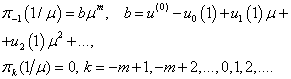 Substituting (3) on (1) we will have for define of functions
Substituting (3) on (1) we will have for define of functions 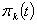
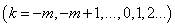 , and
, and 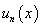
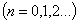 we have the following equations:
we have the following equations: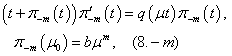
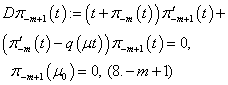
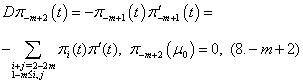
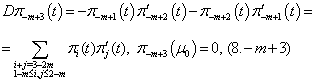
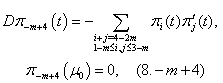
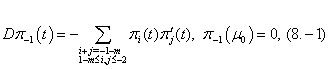
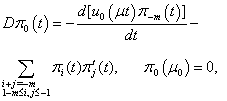
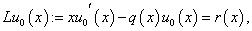
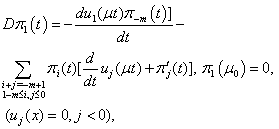
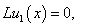
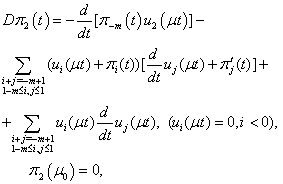
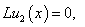
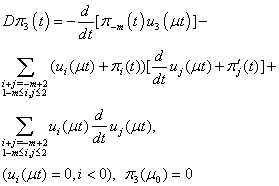
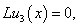
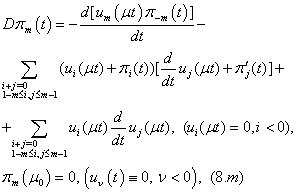
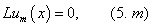
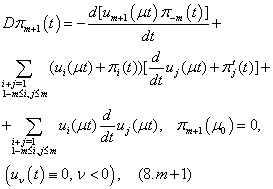
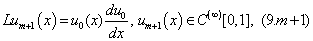
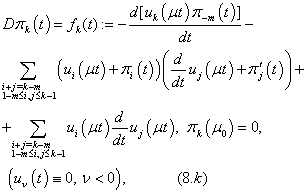
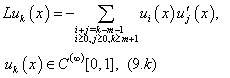 Now we will solve these problems consecutively. We are to prove the existence of the solution of equations (5.0), (5.1), (5.2) that need the following lemma.Lemma 1. The equation
Now we will solve these problems consecutively. We are to prove the existence of the solution of equations (5.0), (5.1), (5.2) that need the following lemma.Lemma 1. The equation 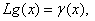
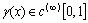 have unique bounded solution from
have unique bounded solution from 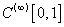 and his have the following view
and his have the following view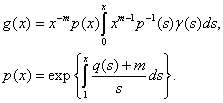
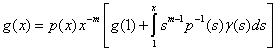 .If we set
.If we set 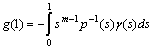 , then we have got (11).From this Lemma follow that equations (9.0), (9.1),… will have unique solutions and
, then we have got (11).From this Lemma follow that equations (9.0), (9.1),… will have unique solutions and 
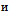
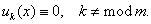 .Theorem 1. If it is hold:
.Theorem 1. If it is hold: 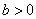 then the problem (8.-m) have unique bounded positive solution in
then the problem (8.-m) have unique bounded positive solution in 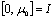 and
and 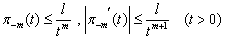 .Here and further we will denote by
.Here and further we will denote by 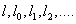 constants, which are do not depend from
constants, which are do not depend from 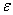 .Proof. In order to proof of existing of the solution of this equation in[17] was applied the following approach. We will rewrite (8.-m) as equation
.Proof. In order to proof of existing of the solution of this equation in[17] was applied the following approach. We will rewrite (8.-m) as equation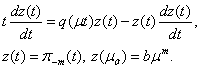 By solving this equation as inhomogeneous equation we have got
By solving this equation as inhomogeneous equation we have got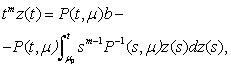
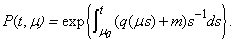 If
If 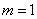 after integrating by parts the equation (12) will reduce to
after integrating by parts the equation (12) will reduce to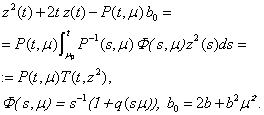
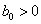 , then by solving this equation as quadratic equation we have got
, then by solving this equation as quadratic equation we have got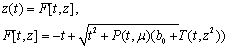 It is proved[17] that this equation will have a unique solution In the class
It is proved[17] that this equation will have a unique solution In the class 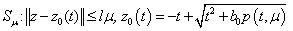 ,
,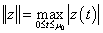 .It is impossible to apply such an approach when
.It is impossible to apply such an approach when 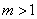 .Really in this case the equation (13) will have the following view:
.Really in this case the equation (13) will have the following view: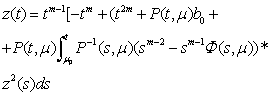 Since
Since 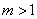 it is singular integral equation and we can not to solve the previous approach.Now we will to solve the equation (8.-m) by method of variation constant of Lagrange. This equation we will rewrite in the form of
it is singular integral equation and we can not to solve the previous approach.Now we will to solve the equation (8.-m) by method of variation constant of Lagrange. This equation we will rewrite in the form of 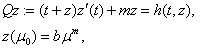
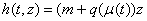 .The problem
.The problem 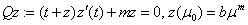 will have the following solution
will have the following solution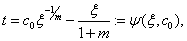
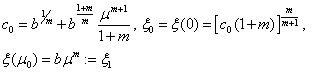 .Thus,
.Thus, 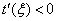 ,
, 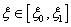 , therefore exists a unique bounded positive strictly decreasing solution
, therefore exists a unique bounded positive strictly decreasing solution 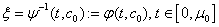 From (15) we have
From (15) we have 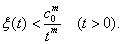
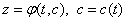 .Then for
.Then for 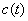 we have the following equation
we have the following equation 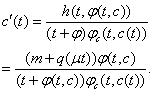
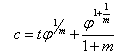 follow
follow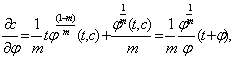
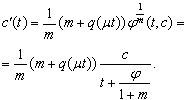 From here we have got
From here we have got 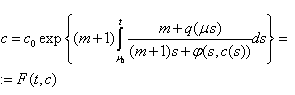 It is evident, that the function
It is evident, that the function 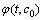 maps
maps 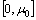 to
to 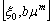 .Operator
.Operator 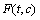 maps the segment
maps the segment 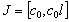 to itself. Using
to itself. Using 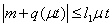 , we have got
, we have got 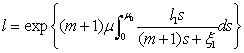 . Now we will proof, that operator F is contracting in J. Since
. Now we will proof, that operator F is contracting in J. Since 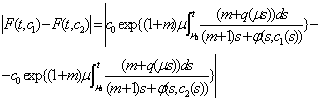 From here applying mean value theorem of Lagrange, we have got
From here applying mean value theorem of Lagrange, we have got 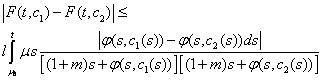 By using (18) we have
By using (18) we have 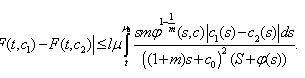 From here by divide this integral to two and by using (16) we have got
From here by divide this integral to two and by using (16) we have got 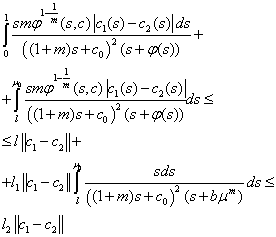 Therefore
Therefore 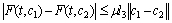 .It is shown, that operator F contracting on J. Now we will solve the problems (4.m+k) (k=1, 2, …). For solving this problem we will use the following: Lemma 2. The equation
.It is shown, that operator F contracting on J. Now we will solve the problems (4.m+k) (k=1, 2, …). For solving this problem we will use the following: Lemma 2. The equation 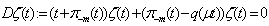 has the a fundamental solution
has the a fundamental solution 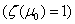
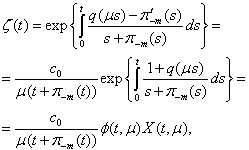 here
here 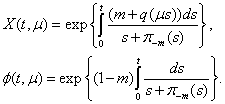 ,.It is evident from terms
,.It is evident from terms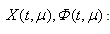
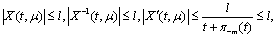
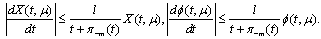 Lemma 3. The inhomogeneous equation (8.k)
Lemma 3. The inhomogeneous equation (8.k)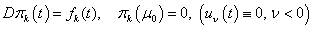 will have the unique solution and
will have the unique solution and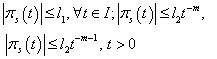 We will prove this lemma for the case
We will prove this lemma for the case 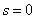 , other cases are proved analogously.(4.-m+1) is homogeneous equation with zero origin conditions, therefore:
, other cases are proved analogously.(4.-m+1) is homogeneous equation with zero origin conditions, therefore: 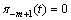 . Analogously:
. Analogously: 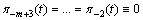 . We have for
. We have for 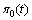 the following problem
the following problem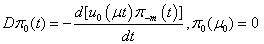
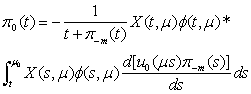 After integrating by parts we have
After integrating by parts we have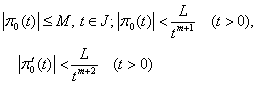
 will prove analogously by dividing integrals into two from
will prove analogously by dividing integrals into two from 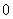 two 1 and from 1 to
two 1 and from 1 to 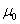 .Therefore we proved the following: Lemma 2. The problem (19) has a unique bounded solution in
.Therefore we proved the following: Lemma 2. The problem (19) has a unique bounded solution in 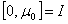 and it is valid for evaluations (20). Analogously equations (8.к) (к=1, 2, …) have unique bounded solutions in
and it is valid for evaluations (20). Analogously equations (8.к) (к=1, 2, …) have unique bounded solutions in 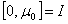 from
from 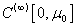 and
and 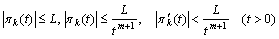 .We proved the following: Theorem 2. Let’s fulfilled condition
.We proved the following: Theorem 2. Let’s fulfilled condition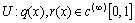 ,
, 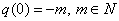 ,
, 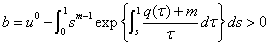 . The solution of the problem (1) will have unique solution and his asymptotic represent in the view (3) and
. The solution of the problem (1) will have unique solution and his asymptotic represent in the view (3) and 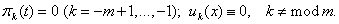
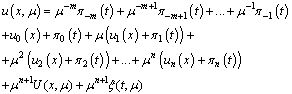
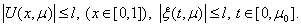 We will prove this lemma for brevity for
We will prove this lemma for brevity for 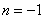 , that is
, that is 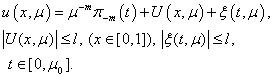
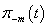 we have the equation (8.-m), for
we have the equation (8.-m), for 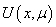 and
and 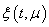 we have got:
we have got: 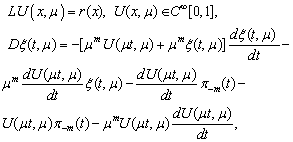
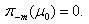
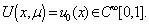 It is from (24) we will go to the integral equation
It is from (24) we will go to the integral equation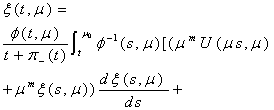
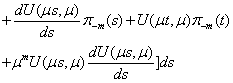 .After integrate by parts the second term we have the weekly perturbed integral equation of Volterra that will have unique bounded solution in
.After integrate by parts the second term we have the weekly perturbed integral equation of Volterra that will have unique bounded solution in  Lemma 3 is proved.
Lemma 3 is proved.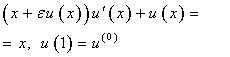
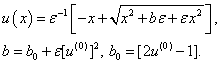
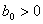 , then (26) exist on interval
, then (26) exist on interval 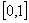 and
and 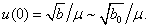
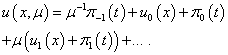
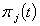 we will take in the form:
we will take in the form: 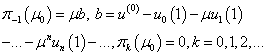 Then for functions
Then for functions 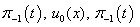 we have the following problems
we have the following problems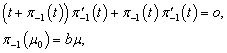
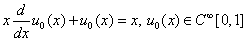 ,
,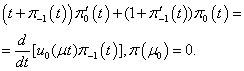 From here we have got
From here we have got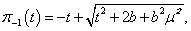
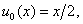
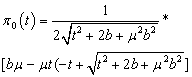 .Therefore we will rewrite (28) in the form
.Therefore we will rewrite (28) in the form 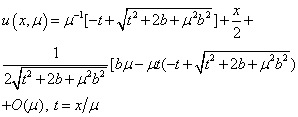
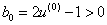 . Since
. Since 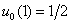 , then
, then 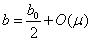 . If we set
. If we set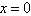 into (29), then
into (29), then 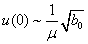 . It will agree with (27).II. We will construct of the solution of the problem (25) by the method of structural matching
. It will agree with (27).II. We will construct of the solution of the problem (25) by the method of structural matching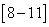 . It is considered instead of (25) the following uniformization equation (see (5))
. It is considered instead of (25) the following uniformization equation (see (5))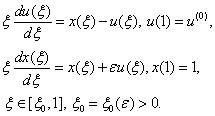
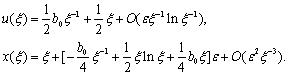
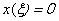 we have got
we have got 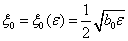 .If we set this meaning to the first equality (31), then
.If we set this meaning to the first equality (31), then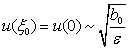 ,That will agree with (27) too.III. Now we will construct the solution of the problem (25) by the method of structural matching[8-11]. a) Firstly we will construct the outer solution (
,That will agree with (27) too.III. Now we will construct the solution of the problem (25) by the method of structural matching[8-11]. a) Firstly we will construct the outer solution (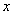 -outer variable and not depend from ) of this problem with the initial condition
-outer variable and not depend from ) of this problem with the initial condition 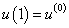 . We will have
. We will have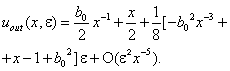
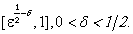 b) Secondly we will construct the inner solution of the problem (25), that satisfy this equation of the singular point
b) Secondly we will construct the inner solution of the problem (25), that satisfy this equation of the singular point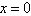 near. For this introduce inner variable
near. For this introduce inner variable 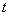 by formula:
by formula: 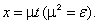 Then equation (25) we will rewrite in the form
Then equation (25) we will rewrite in the form 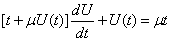
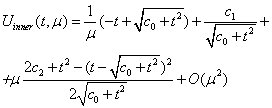
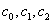 - arbitrary constants. If the outer solution (32) we will rewrite in the inner variable
- arbitrary constants. If the outer solution (32) we will rewrite in the inner variable 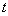 , then
, then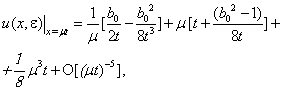
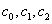 such
such 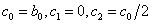 , then the outer solution and inner solution agree and the inner solution will have the form
, then the outer solution and inner solution agree and the inner solution will have the form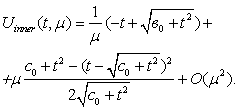
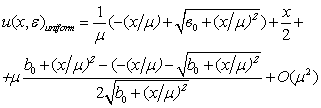 If we will set here
If we will set here 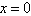 , then
, then 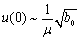 , this agrees with (27).
, this agrees with (27). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML