-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(1): 40-44
doi:10.5923/j.ajms.20130301.06
EQPro. Algorithm for Studying a Special Case of the Initial Distributionof the Markov Transition Matrixwith Theoretical and Numerical Applications
Dejela I. Mahdi , Ali S. Abdul Razak , Nathier Abas Ibrahim
Department of statistics, College of Administration & EconomicsBaghdad University
Correspondence to: Nathier Abas Ibrahim , Department of statistics, College of Administration & EconomicsBaghdad University.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper concentrates on deriving a formula for a special case of the initial distribution of the Markov transition probability matrixwithassumingall the probabilities being equal.A Markov Chain [7]is a mathematical system that undergoes transitions from one to another state. Markov chains have many applications as statistical models of real-world processes. This paper gives a procedure to make the transition probabilities calculation easier.
Keywords: Markov Chain, Transition Probability Matrix, EQPro, (Equal Probabilities), Queuing Models, Inventory System, Storage Models
Cite this paper: Dejela I. Mahdi , Ali S. Abdul Razak , Nathier Abas Ibrahim , EQPro. Algorithm for Studying a Special Case of the Initial Distributionof the Markov Transition Matrixwith Theoretical and Numerical Applications, American Journal of Mathematics and Statistics, Vol. 3 No. 1, 2013, pp. 40-44. doi: 10.5923/j.ajms.20130301.06.
Article Outline
1. Introduction & Achievement
- Markov chains deal with the transition of states of discrete type to describe its behaviourafter n steps. The purpose of this paper is to replace transition probabilities calculations with linear calculations when dealing with Markov transition probability matrices of large order for simplicity. And the algorithm will be applied to different Markov Chain models like Queueing Models, Inventory System and Storage Models[1] [2] [4] for more illustration. In this paper we assume that
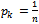 .
.2. Theoretical Framework
- A transition probability matrix P is a
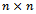 matrix, where the terms in each row add 1. The expression of this type of matrix is:
matrix, where the terms in each row add 1. The expression of this type of matrix is: | (1) |
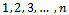 are the states Where:-
are the states Where:- 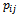 is the probability of I moving to j- (i, j) are the corresponding position of each element in the transition matrix. i.e.
is the probability of I moving to j- (i, j) are the corresponding position of each element in the transition matrix. i.e.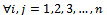 And:
And: | (2) |
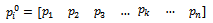 | (3) |
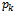 is the initial probability of state k ,where
is the initial probability of state k ,where 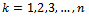 Usually
Usually 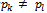 for any
for any 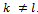 .When
.When 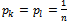 ,this means that the initial distribution is equally likely then we will derive a general formula to get:
,this means that the initial distribution is equally likely then we will derive a general formula to get: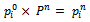 | (4) |
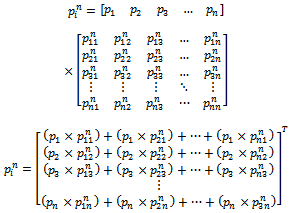
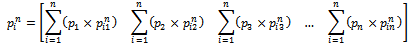 Where
Where 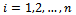 By replacing
By replacing 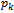 with
with 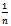 we get:
we get: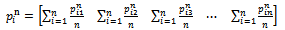 | (6) |
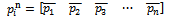 | (7) |
3. Application
- The application will cover two parts; First, a numerical part by using the EQPro algorithm to illustrate the previous section. And second with applications of Markov chains transition probability matrix.
3.1. EQPRO Algorithm Procedure
- To illustrate the theoretical part, we will use an EQPRO Algorithm for generating Markov transition matrices with different sizes. The software used for generating matrices is the “Matlab R2009b” [3] , which is flexible when dealing with matrices.1- Generate a random matrix of dimension
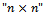 follows the discrete uniform distribution,
follows the discrete uniform distribution,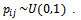 2- The resulting matrix satisfies that:
2- The resulting matrix satisfies that: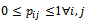 Next, the arithmetic mean for each column is computed as follows.3- By transposing the matrix, we check that the elements in a fixed row add 1; i.e.
Next, the arithmetic mean for each column is computed as follows.3- By transposing the matrix, we check that the elements in a fixed row add 1; i.e.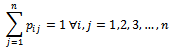 In the Matlabsoftware is:-
In the Matlabsoftware is:-
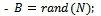

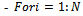
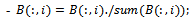
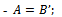
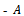 We illustration theEQPro algorithm in different sizes of matrices from size2 to size 8 with different steps of transition probability matrix:1- Size 2:
We illustration theEQPro algorithm in different sizes of matrices from size2 to size 8 with different steps of transition probability matrix:1- Size 2: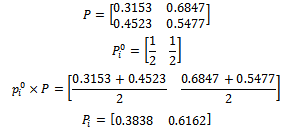 2- Size 3 with 2-step:
2- Size 3 with 2-step: 3- Size 4 with 5-step:
3- Size 4 with 5-step: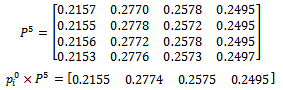 4- Size 5 with 4-step:
4- Size 5 with 4-step: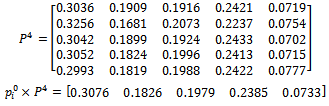 5- Size 6 with 2-step:
5- Size 6 with 2-step: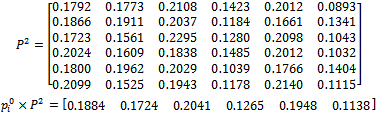 6- Size 7:
6- Size 7: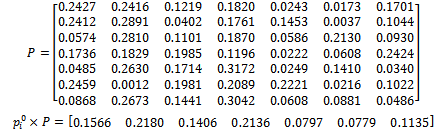 7- Size 8 with 2-step:
7- Size 8 with 2-step: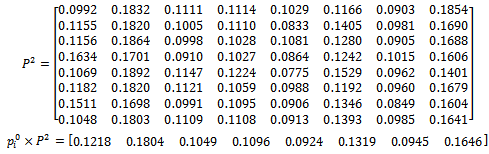
3.2. Applied Markov Chains
- Before, the derived formula will be applied to some problems based modelled by Markov Chains:
3.2.1. Queuing Models
- A system consisting of a service facility, a process of arrival of customers who wish to be served by the facility, and the process of service is called a Queuing system [1] [2] [4] [5].Concretely, the M/G/1 Queue [1] [2] [4] [5] is based on a Markov chain with transition probability matrix:
 Suppose that the M/G/1 queue described above is modified to incorporate a finite waiting room of size N. Assuming that customers arriving at the system depart without service when the waiting room is full, the transition probability matrix of the Markov chain takes the form:
Suppose that the M/G/1 queue described above is modified to incorporate a finite waiting room of size N. Assuming that customers arriving at the system depart without service when the waiting room is full, the transition probability matrix of the Markov chain takes the form: Where we have written:
Where we have written: 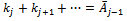 Equation (6) in this matrix. The result is:
Equation (6) in this matrix. The result is: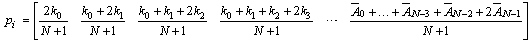 Hence, each element
Hence, each element 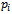 in the initial probability distribution is expressible as:
in the initial probability distribution is expressible as: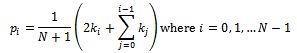 And
And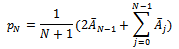
3.2.2. Inventory Systems
- An inventory system is a facility in which items of merchandise and materials are stocked in order to meet demands [1] [2] [5] .Its transition probability matrix P is given by (only nonzero elements are shown)
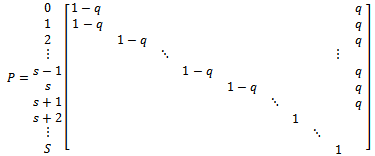 Equation (6) in this matrix. The result is:
Equation (6) in this matrix. The result is: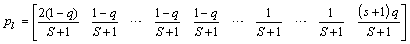
3.2.3. Storage Models
- In storage theory problems related to situations such as storing water in a reservoir are considered. These problems are similar to inventory problems since the basic feature is storing a commodity until its released to or claimed by another party[1] [2] [6].
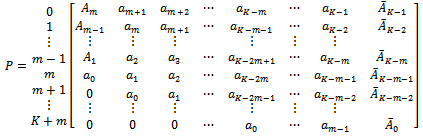 Equation (6) in this matrix. The result is:
Equation (6) in this matrix. The result is: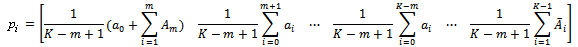 When
When 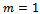 , a simple recursive approach can be suggested in deriving the limiting distribution of the Markov chain. In this case we have:
, a simple recursive approach can be suggested in deriving the limiting distribution of the Markov chain. In this case we have: Equation (6) in this matrix. The result is:
Equation (6) in this matrix. The result is: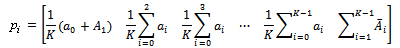
4. Conclusions
- As we have seen, it is easier to deal with numerical calculations rather than transition probabilities calculations, especially when the transition probability matrix contains a lot of zeros. So we hope this paper gives the first step in deriving an easy formula for the initial distribution with equal probability for the “Applied Markov Chains”.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML