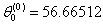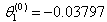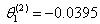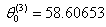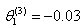-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2013; 3(1): 32-39
doi:10.5923/j.ajms.20130301.05
A Jackknife Approach to Error-Reduction in Nonlinear Regression Estimation
Obiora-Ilouno H. O. 1, Mbegbu J. I. 2
1Nnamdi Azikiwe University, Awka, Nigeria
2Department of Mathematics University of Benin, Benin City Edo State, Nigeria
Correspondence to: Obiora-Ilouno H. O. , Nnamdi Azikiwe University, Awka, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The problems involving the use of jackknife methods in estimating the parameters of non linear regression models have been identified in this paper. We developed new algorithms for the estimation of nonlinear regression parameters. For estimating these parameters, computer programs were written in R for the implementation of these algorithms. We adopted the Gauss-Newton method based on Taylor’s series to approximate the nonlinear regression model with the linear term, and subsequently employ least square method iteratively. In the estimation of the nonlinear regression parameters, the results obtained from numerical problems using the Jackknife based algorithm developed yielded a reduced error sum of squares than the analytic result. As the number of d observations deleted in each resampling stage increases, the error sum of squares reduces minimally. This reveals the appropriateness of the new algorithms for the estimation of nonlinear regression parameters and in the reduction of the error terms in nonlinear regression estimation.
Keywords: Non- linear Regression, Jackknife Algorithm, Delete–d, Gauss–Newton
Cite this paper: Obiora-Ilouno H. O. , Mbegbu J. I. , A Jackknife Approach to Error-Reduction in Nonlinear Regression Estimation, American Journal of Mathematics and Statistics, Vol. 3 No. 1, 2013, pp. 32-39. doi: 10.5923/j.ajms.20130301.05.
Article Outline
1. Introduction
- The Jackknife is a resampling technique use for estimating the bias and standard error of an estimator and provides an approximate confidence interval for the parameter of interest. The principle behind jackknife method lies in systematically recomputing the statistic leaving out one or more observation(s) at a time from the sample set thereby generating n separate samples each of size n-1 or n-d respectively. From this new set of replicates of the statistic, an estimate for bias and the variance of the statistic can be calculated[3].[5] used linear regression analysis to examine the relationship between the Fish Age (FA) as response variable, Total Length (TL) and the Otolith Length (OL) as predictor variables. They examined dependence of FA on TL and OL using bootstrap and Jackknife algorithm.[5] used bootstrap to study linear regression model of the form
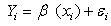 with error term
with error term  being independent. In[5], the bootstrap errors
being independent. In[5], the bootstrap errors 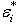 are drawn with replacement from the set of estimated residuals. Response values
are drawn with replacement from the set of estimated residuals. Response values 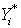 are constructed as the sum of an initial estimate for
are constructed as the sum of an initial estimate for and
and  .[6] used bootstrap method to investigate the effects of sparsity of data for the binary regression model. He discovered that the bootstrap method provided robust (accurate) result for the sparse data.[4] considers regression and correlation models, and obtain the bootstrap approximation to the distribution of least squares estimates.[2] provides algorithm for data analysis and bootstrap for the construction of confidence sets and tests in classical models which involves exact or asymptotic distribution.[14] proposes a class of weighted jackknife variance estimators for the ordinary least squares estimator by deleting any fixed number of observations at a time. He observed that the weighted jackknife variance estimators are unbiased for homoscedastic errors.[11] proposes an unbiased ridge estimator using the jackknife procedure of bias reduction. They demonstrated that the jackknife estimator had smaller bias than the generalized ridge estimator (GRE).[1] proposes Modified jackknife ridge regression estimator (MJR) by combining the ideas of GRR and JRR estimators. In their article, they proposed a new estimator named generalized jackknife ridge regression estimator (GJR) by generalizing the MJR. Their result showed that the new proposed estimator (GJR) is superior in the mean square error (MSE) than the generalized ridge regression estimator in regression analysis.
.[6] used bootstrap method to investigate the effects of sparsity of data for the binary regression model. He discovered that the bootstrap method provided robust (accurate) result for the sparse data.[4] considers regression and correlation models, and obtain the bootstrap approximation to the distribution of least squares estimates.[2] provides algorithm for data analysis and bootstrap for the construction of confidence sets and tests in classical models which involves exact or asymptotic distribution.[14] proposes a class of weighted jackknife variance estimators for the ordinary least squares estimator by deleting any fixed number of observations at a time. He observed that the weighted jackknife variance estimators are unbiased for homoscedastic errors.[11] proposes an unbiased ridge estimator using the jackknife procedure of bias reduction. They demonstrated that the jackknife estimator had smaller bias than the generalized ridge estimator (GRE).[1] proposes Modified jackknife ridge regression estimator (MJR) by combining the ideas of GRR and JRR estimators. In their article, they proposed a new estimator named generalized jackknife ridge regression estimator (GJR) by generalizing the MJR. Their result showed that the new proposed estimator (GJR) is superior in the mean square error (MSE) than the generalized ridge regression estimator in regression analysis. 2. Materials and Method
- Given a model of the form
 | (2.1) |
 are the predictor variables and the error term
are the predictor variables and the error term  independently identically distributed and are uncorrelated.Equation (2.1) is assumed to be intrinsically nonlinear. Suppose we have a sample of n observations on the
independently identically distributed and are uncorrelated.Equation (2.1) is assumed to be intrinsically nonlinear. Suppose we have a sample of n observations on the 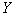 and
and  , then, we can write
, then, we can write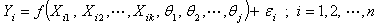 | (2.2) |
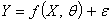 | (2.3) |
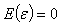 The error sum of squares for the nonlinear model is defined as
The error sum of squares for the nonlinear model is defined as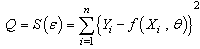 | (2.4) |
 , these estimates minimize the
, these estimates minimize the  . The least square estimates of
. The least square estimates of 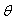 are obtained by differentiating (2.4) with respect to
are obtained by differentiating (2.4) with respect to 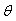 , equate to zero and solve for
, equate to zero and solve for 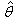 , this results in J normal equations:
, this results in J normal equations: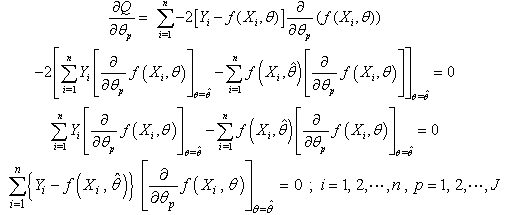 | (2.5) |
 which is the deterministic component of
which is the deterministic component of  | (2.6) |
 be the initial approximate value of
be the initial approximate value of  . Adopting Taylor’s series expansion of
. Adopting Taylor’s series expansion of  about
about  , we have the linear approximation
, we have the linear approximation | (2.7) |
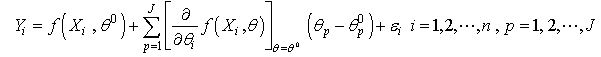 | (2.8) |
 Hence, equation (2.8) becomes
Hence, equation (2.8) becomes | (2.9) |
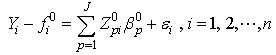 | (2.10) |
 | (2.11) |
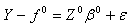 | (2.12) |
 We obtain the Sum of squares error
We obtain the Sum of squares error 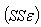

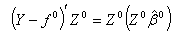 | (2.13) |
 | (2.14) |
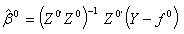 | (2.15) |
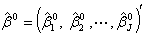 minimizes the error sum of squares,
minimizes the error sum of squares,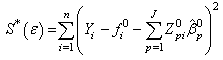 | (2.16) |
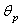 of non-linear regression (2.1) are
of non-linear regression (2.1) are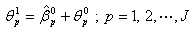 | (2.17) |
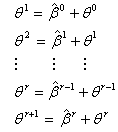 Thus
Thus 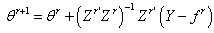 | (2.18) |
 are the least squares estimates of
are the least squares estimates of  obtained at the
obtained at the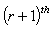 iterations. The iterative process continues until
iterations. The iterative process continues until  where
where 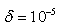 is the error tolerance [12][7]After each iteration,
is the error tolerance [12][7]After each iteration, 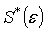 is evaluated to check if a reduction in its value has actually been achieved. At the end of the
is evaluated to check if a reduction in its value has actually been achieved. At the end of the  iteration, we have
iteration, we have  | (2.19) |
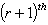 iteration are:
iteration are: 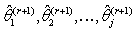 .
. 2.1. Jackknife Delete-One Algorithm for the Estimation of Non-linear Regression Parameters
- Let
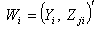 vector denotes the values associated with
vector denotes the values associated with 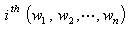 observation sets. The steps of the delete-one jackknife regression are as follows.Given randomly drawn sample of size n from a population and label the elements of the vector
observation sets. The steps of the delete-one jackknife regression are as follows.Given randomly drawn sample of size n from a population and label the elements of the vector 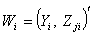 as the vector
as the vector  be the response variables,
be the response variables, 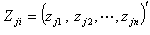 is the matrix of dimension
is the matrix of dimension 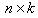 for the predictor variables, where
for the predictor variables, where 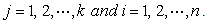 1. Omit first row of the vector
1. Omit first row of the vector 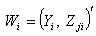 and label remaining
and label remaining 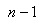 observation sets
observation sets  and
and 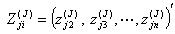 as the first delete-one Jackknife sample
as the first delete-one Jackknife sample  2. Calculate the least square estimates for nonlinear regression coefficient from the first jackknife sample;
2. Calculate the least square estimates for nonlinear regression coefficient from the first jackknife sample; 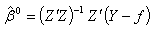 .3. Compute
.3. Compute 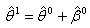 using the Gauss-Newton method, the
using the Gauss-Newton method, the 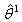 value is treated as the initial value in the first approximated linear model.4. We return to the second step and again compute
value is treated as the initial value in the first approximated linear model.4. We return to the second step and again compute 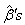 .At each iteration, new
.At each iteration, new 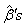 represent increments that are added to the estimates from the previous iteration according to step 3 and eventually find
represent increments that are added to the estimates from the previous iteration according to step 3 and eventually find 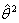 , which is
, which is 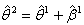 up to
up to  .5. Stopping Rule; this iteration process continues until
.5. Stopping Rule; this iteration process continues until , where
, where 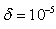 , for the values of
, for the values of 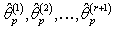 from the first delete-one Jackknife estimates
from the first delete-one Jackknife estimates 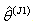 .6. Then, omit second row of the vector
.6. Then, omit second row of the vector 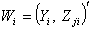 and label remaining n-1 sized observation sets
and label remaining n-1 sized observation sets 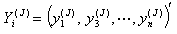 and
and 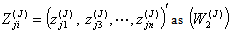 and repeat steps 2 to 5 above for the estimate of regression coefficients
and repeat steps 2 to 5 above for the estimate of regression coefficients . Similarly, omit each one of the n observation sets and estimate the non linear regression coefficients as in the step 2 to 5 above for
. Similarly, omit each one of the n observation sets and estimate the non linear regression coefficients as in the step 2 to 5 above for  alternately, where
alternately, where 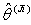 is Jackknife regression coefficient vector estimated after deleting of
is Jackknife regression coefficient vector estimated after deleting of 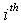 observation set from
observation set from 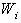 .7. Obtain the probability distribution
.7. Obtain the probability distribution 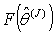
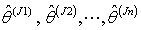 of Jackknife estimates
of Jackknife estimates 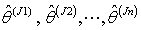 .8. Calculate the jackknife regression coefficient estimate which is the mean of the
.8. Calculate the jackknife regression coefficient estimate which is the mean of the 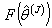 distribution[9] as;
distribution[9] as;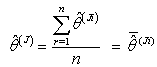 | (2.21) |
2.2. Jackknife Delete-d Algorithm for Estimation of Non-Linear Regression
- Let
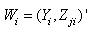 vector denotes the values associated with
vector denotes the values associated with 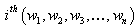 observation sets. Draw a random sample of size n from the observation set (population) and label the elements of each vector
observation sets. Draw a random sample of size n from the observation set (population) and label the elements of each vector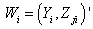 as the vector
as the vector 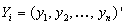 be the response variables, and
be the response variables, and 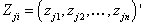 be the matrix of dimension n × k for the predictor variables, where j=1, 2, …, k and i = 1, 2 , …, n.Step 1: Divide the sample into “s” independent group of size d.Step 2: Omit first d observation set from full sample at a time and estimate the nonlinear regression parameter
be the matrix of dimension n × k for the predictor variables, where j=1, 2, …, k and i = 1, 2 , …, n.Step 1: Divide the sample into “s” independent group of size d.Step 2: Omit first d observation set from full sample at a time and estimate the nonlinear regression parameter 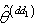 from (n - d) remaining observation set using the least square estimate for the nonlinear regression parameter from the first delete-d sample;
from (n - d) remaining observation set using the least square estimate for the nonlinear regression parameter from the first delete-d sample;  .Step 3: Compute
.Step 3: Compute 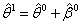 using the Gauss-Newton method, the
using the Gauss-Newton method, the 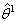 value is assumed as the initial value in the first approximation.Step 4: Repeat the second step and again compute
value is assumed as the initial value in the first approximation.Step 4: Repeat the second step and again compute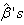 . At each iteration, new
. At each iteration, new 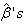 represent increments that are added to the estimates
represent increments that are added to the estimates 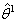 from the previous iteration according to step 3 and eventually obtain
from the previous iteration according to step 3 and eventually obtain  up to
up to  and consequently
and consequently 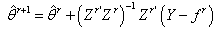 Step 5: Stopping Rule; the iteration process continues until
Step 5: Stopping Rule; the iteration process continues until , (where
, (where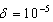 is the tolerance magnitude) and the parameters
is the tolerance magnitude) and the parameters 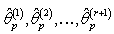 are computed from
are computed from 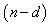 delete-d samples
delete-d samples  Step 6: Omit second d observation set from full sample at a time and estimate the nonlinear regression parameters
Step 6: Omit second d observation set from full sample at a time and estimate the nonlinear regression parameters  from remaining
from remaining  observation set based on the delete-d sample; and repeat step 3 to step 5 for the second delete-d sample.Step 7: Alternately omit each d of the n observation set and estimate the parameters as
observation set based on the delete-d sample; and repeat step 3 to step 5 for the second delete-d sample.Step 7: Alternately omit each d of the n observation set and estimate the parameters as 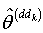 where
where 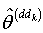 is the jackknife regression parameter vector estimated after deletion of
is the jackknife regression parameter vector estimated after deletion of  d observation set from full sample, for k =1,2,…,s; where
d observation set from full sample, for k =1,2,…,s; where 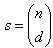 , and
, and 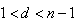 ; where d is an integer.Step 8: Obtain the probability distribution
; where d is an integer.Step 8: Obtain the probability distribution 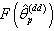 of nonlinear regression parameter estimates
of nonlinear regression parameter estimates 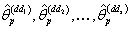 .Step 9: Calculate the nonlinear regression parameter estimate
.Step 9: Calculate the nonlinear regression parameter estimate 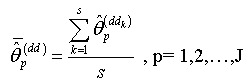 | (2.22) |
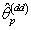 isWhere
isWhere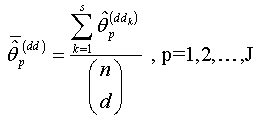 | (2.23) |
|
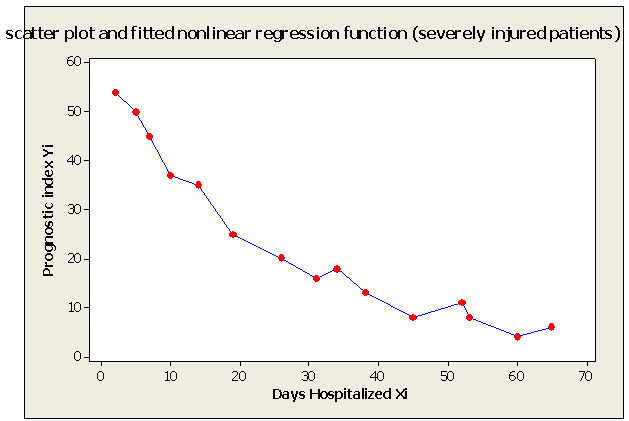 | Figure 1. Scatter Plot and Fitted Nonlinear Regression Function - Severely Injured Patients Example |
3. Results and Discussion
- Table shows the result for the parameters estimates and the error sum of squares obtained in each iteration.
|
|
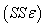 for the starting values has been reduced in the first iteration and also further reduced in the second, third iterations respectively. The third iteration led to no change in either the estimates of the coefficient or the least squares
for the starting values has been reduced in the first iteration and also further reduced in the second, third iterations respectively. The third iteration led to no change in either the estimates of the coefficient or the least squares criterion measure. Hence, convergence is achieved, and the iterations end. Table 3 shows the results of the analytical and the Jackknifes computation. The fitted regression functions for both analytical and Jackknifes delete -1 computation are:
criterion measure. Hence, convergence is achieved, and the iterations end. Table 3 shows the results of the analytical and the Jackknifes computation. The fitted regression functions for both analytical and Jackknifes delete -1 computation are: 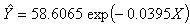 and
and 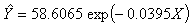 respectively. The sums of squares error for the analytical and Jackknifes computation are also shown in the table 3. Also, as the number of d observations deleted in each resampling stage increases, the error sum of squares reduces minimally.
respectively. The sums of squares error for the analytical and Jackknifes computation are also shown in the table 3. Also, as the number of d observations deleted in each resampling stage increases, the error sum of squares reduces minimally. 4. Conclusions
- We have described the Jackknife algorithm in estimation of the parameters of nonlinear regression model implementation in exponential regression model. The results obtained as shown in Tables 2 and 3 indicate that the Jackknife methods produced a minimum error sum of squares than the analytical method. We also observe that as the number of d observations deleted in each resampling stage increases, the error sum of squares reduces minimally. Hence, the Jackknife techniques yielded approximately the same inference as the analytical method with a better reduced error sum of squares.
Appendix
- Delete One Jackknife Result for the Estimates of Parameters
 y <- c(54,50,45,37,35,25,20,16,18,13,8,11,8,4,6)x <- c(2,5,7,10,14,19,26,31,34,38,45,52,53,60,65)data=cbind(y,x)initial=c(56.66,-0.03797)expo=jack(data,2,1,initial) #Run the following to view the jacknife resultstheta_0=mean(expo[,1])theta_0[1] 58.59964theta_1=mean(expo[,2])theta_1[1] -0.03958257SSE=mean(expo[,3])SSE[1] 45.73693> expo [,1] [,2] [,3][1,] 58.72515 -0.03967516 49.42362[2,] 57.69838 -0.03906341 44.59006[3,] 58.40287 -0.03950187 49.05152[4,] 59.16565 -0.03961937 42.57768[5,] 58.45181 -0.03973249 47.48378[6,] 58.66917 -0.03904419 41.73934[7,] 58.54728 -0.03931089 48.45668[8,] 58.48971 -0.03921048 47.87337[9,] 58.92722 -0.04049873 40.86874[10,] 58.60389 -0.03957958 49.45880[11,] 58.36243 -0.03902207 45.56932[12,] 59.04047 -0.04053060 35.99040[13,] 58.70595 -0.03980039 48.74806[14,] 58.44419 -0.03925252 47.21911[15,] 58.76037 -0.03989685 47.00351Deleted (= 5) E Result for the Estimates of Parameters
y <- c(54,50,45,37,35,25,20,16,18,13,8,11,8,4,6)x <- c(2,5,7,10,14,19,26,31,34,38,45,52,53,60,65)data=cbind(y,x)initial=c(56.66,-0.03797)expo=jack(data,2,1,initial) #Run the following to view the jacknife resultstheta_0=mean(expo[,1])theta_0[1] 58.59964theta_1=mean(expo[,2])theta_1[1] -0.03958257SSE=mean(expo[,3])SSE[1] 45.73693> expo [,1] [,2] [,3][1,] 58.72515 -0.03967516 49.42362[2,] 57.69838 -0.03906341 44.59006[3,] 58.40287 -0.03950187 49.05152[4,] 59.16565 -0.03961937 42.57768[5,] 58.45181 -0.03973249 47.48378[6,] 58.66917 -0.03904419 41.73934[7,] 58.54728 -0.03931089 48.45668[8,] 58.48971 -0.03921048 47.87337[9,] 58.92722 -0.04049873 40.86874[10,] 58.60389 -0.03957958 49.45880[11,] 58.36243 -0.03902207 45.56932[12,] 59.04047 -0.04053060 35.99040[13,] 58.70595 -0.03980039 48.74806[14,] 58.44419 -0.03925252 47.21911[15,] 58.76037 -0.03989685 47.00351Deleted (= 5) E Result for the Estimates of Parameters  y <- c(54,50,45,37,35,25,20,16,18,13,8,11,8,4,6)x <- c(2,5,7,10,14,19,26,31,34,38,45,52,53,60,65)data=cbind(y,x)initial=c(56.66,-0.03797)expo=jack(data,2,5,initial)#Run the following to view the jacknife resultstheta_0=mean(expo[,1])theta_0[1] 58.51474theta_1=mean(expo[,2])theta_1[1] -0.03953024SSE=mean(expo[,3])SSE[1] 30.75165[1,] 58.67728 -0.03959126 27.73554[2,] 58.17681 -0.03846691 38.39546[3,] 59.16003 -0.04070913 29.55899[4,] 59.68595 -0.04223456 20.55436[5,] 59.23983 -0.04121757 22.01381[6,] 59.70170 -0.04224374 18.53772[7,] 58.67701 -0.03992907 35.55294[8,] 59.17548 -0.04102820 33.88313[9,] 58.75452 -0.04008201 33.77203[10,] 59.75422 -0.04241509 20.84062
y <- c(54,50,45,37,35,25,20,16,18,13,8,11,8,4,6)x <- c(2,5,7,10,14,19,26,31,34,38,45,52,53,60,65)data=cbind(y,x)initial=c(56.66,-0.03797)expo=jack(data,2,5,initial)#Run the following to view the jacknife resultstheta_0=mean(expo[,1])theta_0[1] 58.51474theta_1=mean(expo[,2])theta_1[1] -0.03953024SSE=mean(expo[,3])SSE[1] 30.75165[1,] 58.67728 -0.03959126 27.73554[2,] 58.17681 -0.03846691 38.39546[3,] 59.16003 -0.04070913 29.55899[4,] 59.68595 -0.04223456 20.55436[5,] 59.23983 -0.04121757 22.01381[6,] 59.70170 -0.04224374 18.53772[7,] 58.67701 -0.03992907 35.55294[8,] 59.17548 -0.04102820 33.88313[9,] 58.75452 -0.04008201 33.77203[10,] 59.75422 -0.04241509 20.84062 [2994,] 59.78918 -0.04239372 16.85996[2995,] 59.39368 -0.04150764 18.60413[2996,] 58.89694 -0.04038925 32.77863[2997,] 59.84530 -0.04254249 17.11752[2998,] 58.80620 -0.04000943 30.68688[2999,] 59.26868 -0.04100269 29.02210[3000,] 58.87835 -0.04014695 28.89213[3001,] 58.37072 -0.03902467 40.60791[3002,] 59.35796 -0.04123589 29.70771[3003,] 59.01265 -0.04042930 27.88792
[2994,] 59.78918 -0.04239372 16.85996[2995,] 59.39368 -0.04150764 18.60413[2996,] 58.89694 -0.04038925 32.77863[2997,] 59.84530 -0.04254249 17.11752[2998,] 58.80620 -0.04000943 30.68688[2999,] 59.26868 -0.04100269 29.02210[3000,] 58.87835 -0.04014695 28.89213[3001,] 58.37072 -0.03902467 40.60791[3002,] 59.35796 -0.04123589 29.70771[3003,] 59.01265 -0.04042930 27.88792
References
| [1] | F. SH. Batah, T. V. Ramnathan and S. D. Gore, The Efficiency of Modified Jackknife and Ridge Type Regression Estimators: A comparison, Surveys in Mathematics and its pplications 24 No.2 (2008), 157-174. |
| [2] | Beran, R., The Impact of the Bootstrap on Statistical Algorithms and Theory, Statist. Science, Mathematical Reviews (Maths Sci. Net) Vol. 18, No. 2, pp. 175-184, 2003. |
| [3] | Efron, B. and Tibshirani, R.J., An Introduction to the Bootstrap, Library of Congress Cataloging in Publication Data, CRC Press ,Boca Raton, Florida,60-82, 1998. |
| [4] | Freedman, D.A., Bootstrapping Regression Models, Annals of Statistical Statistics, Vol. 9, 2, pp. 158-167, 1981. |
| [5] | Hardle, W. and Mammen, E., Comparing Nonparametric versus Parametric Regression Fits. Annals of Statistics, Vol. 21, pp. 1926-1947, 1993. |
| [6] | Mohammed, Z. R., Bootstrapping: A Nonparametric Approach to Identify the Effect of Sparsity of Data in the Binary Regression Models, Journal of Applied Sciences, Network for Scientific Information , Asian, Vol. 8, No. 17, pp. 2991-2997, 2008. |
| [7] | Nduka, E. C., Principles of Applied Statistics 1, Regression and Correlation Analyses, Crystal Publishers, Imo State, Nigeria, 1999. |
| [8] | Neter, J., Kutner, M.H., Nachtsheim, C.J. and Wasserman, W., Fourth Edition, Mc-Grow Hill, U.S.A, pp 429-431, 531-536, 1996. |
| [9] | Obiora-Ilouno, H.O. and Mbegbu, J.I, Jackknife Algorithm for the Estimation of Logistic Regression Parameters, Journal of Natural Sciences Research, IISTE UK, Vol.2, No.4, 74-82, 2012. |
| [10] | Sahinler, S. and Topuz, D., Bootstrap and Jackknife Resampling Algorithm for Estimation of Regression Parameters, Journal of Applied Quantitative Method, Vol. 2, No. 2, pp.188-199, 2007. |
| [11] | Singh, B, Chuubey, Y. P. and Dwivedi, T.D., An Almost Unbiased Ridge Estimator. Sankhya series, 48, 342-36, 1986. |
| [12] | Smith, H. and Draper, N. R., Applied Regression Analysis, Third Edition, Wiley- Interscience, New York, 1998. |
| [13] | Venables, W. N and Smith, An Introduction to R, A Programming Environment for Data Analysis and Graphics, Version 2.6.1, pp. 1-100, 2007. |
| [14] | WU, C.F.C., Jackknife, Bootstrap and other Resampling Methods in Regression Analysis. The Annals of Statistics Vol. 14, No.4, 1261 -1295, 1986. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML ) for data in Table 1
) for data in Table 1