1. Introduction

By ring we mean an associative ring that need not have an identity. In this paper, we study a new class of left quasi-Artinian Modules, which is a generalization of left Artinian modules. First we study the problems of finding conditions which are equivalent to the definition of left quasi-Artinian Module(Theorem 1.2). Then we show that the class of left quasi-Artinian Modules is Q-closed, S-closed and E-closed.

In section two we study the module structures over left quasi-Artinian ring, in particular we prove that if R is a left quasi-Artinian ring, then every finitely generated left R-module M is a left quasi-Artinian(Theorem 2.1)Finally we show that: If R be a ring, N = N(R), then R is a left quasi-Artinian if and only if N is nilpotent and each of the 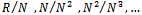is left quasi-Artinian R-module (Theorem 2.4).

In section three we describe the ideal structures and we give some classification, in particular we prove that if I is a non-nilpotent left ideal in a left quasi-Artinian ring, then I contains a non-zero idempotent element (Theorem 3.2). Next we prove that if R is a semi-prime left quasi-Artinian ring and I be a non-zero left ideal of R, then I=Re for some non-zero idempotent e in R (Theorem 3.5).

1.1. Definitions and Basic Properties

Let M be a left R-module. We say that M is a left quasi-Artinian Module if for every descending chain 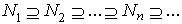of left R-submodules of M, there exist 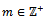such that 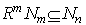for all n.

It is clear that any left Artinian module is left quasi-Artinian and it is easy to prove the following

Lemma1.1

Let M be a left R-module.

(a) If RM= 0, then M is a left quasi-Artinian.

(b)If R has an identity and M is unitary ,then M is left quasi-Artinian if and only if M is left Artinian.

Now we prove the following which is a characterization of left quasi-Artinian modules.

Theorem1.2

Let M be a left R-module. Then the following conditions are equivalent:

of left R-submodules of M such (a) In every non-empty collection

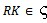, then , there exists a minimal element. that if

(b) For every descending chain of left R-submodules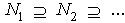

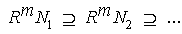there exists such that a descending chain terminates.

(c)M is left quasi-Artinian .

(d) For every non-empty collectionof left R-submodules of M, there exists 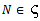and 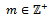such that 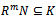for any ,

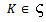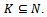Proof:

(a)⇒ (b) Suppose that 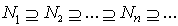is a descending chain of left R-submodules of M but the descending chain 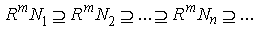of left R-submodules of M does not terminate for all 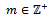. Therefore the collection 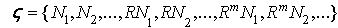is a nonempty collection of R-submodules and for all 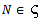we have 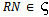. Hence 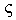has no minimal element, which is a contradiction.

(b) ⇒ (c) Let 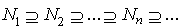be any descending chain of left R-submodules of M then there exists 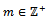such that 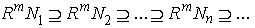form a descending chain of left R-submodules of M and by (b) there exists 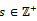such that 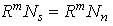for all 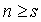, but 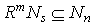for all 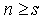. Take t = max {m, s} then 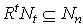for all n, hence M is a left quasi-Artinian .

(c) ⇒ (d) Let 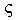be a non-empty collection of left R-submodules of M such that for each 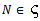and 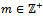, there exists 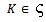such tha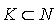t , but 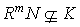. Now let 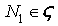then there exists 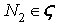such that 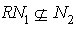,where 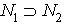, but 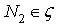hence there exists 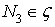, such that 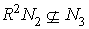, where 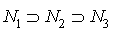continuing in this manner we can construct an infinite descending chain 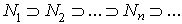of left R-submodules of M such that 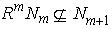,m=1,2,… .Hence 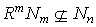for some n, which is a contradiction.

(d) ⇒ (a) Let be a non-empty collection of left R-submodules of M such that for all 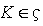. Then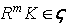, for all 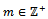. But 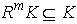for all 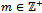, hence by (d) there exists an 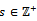such that 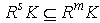for all 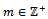.Therefore if 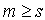, then 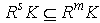and 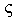has a minimal element.

Next we prove the following:

Proposition1.3

Let M be a left R-module. If RM is left Artinian, then M is left quasi-Artinian .

Proof:

be a descending chain of left R-submodules of M,

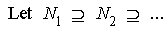R-submodulesof RM. 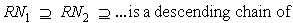then

But RM is left Artinian, hence there exists 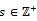such that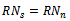

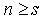. Therefore 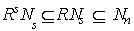. For all n Hence M is left quasi-Artinian.

Remark: The converse of Proposition 1.3,needs not be true as the following example shows:

Let 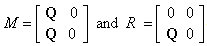. Then M is left quasi-Artinian

R-module,but 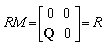is not left Artinian.

Now let Т be a class of modules. Then we say that Т is S-closed if N is a submodule of M and 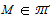then N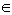Т .We say that Т is Q-closed if 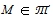and N is a submodule of M, then 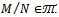We say that Т is E-closed if N is a submodule of M and N , 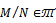, then M 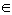Т.

Proposition 1.4

Let Т be the class of left quasi-Artinian modules. Then

(a)Т is S-closed . (b) Т is Q-closed.(c) Т is E-closed.

Proof:

(a) is clear

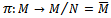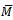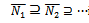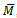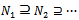(b) Suppose that M is a left quasi-Artinian R-module and N is submodule of M. Let be the natural homomorphism of left quasi-Artinian module onto . Then is a descending chain of submodules of , and is a descending chain of R- submodules of M, where 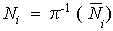but M is left quasi-Artinian, hence there exists 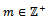such that 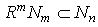for all n. But 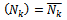. Hence 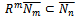for all n. Therefore 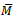is left quasi-Artinian.

(c)Suppose that N be an R-submodule of M and 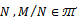. Let be a descending chain of left R-submodules of M. Then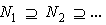

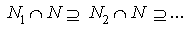is a descending chain of R-submodules of N. But 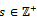such that left quasi-Artinian, hence there existN is

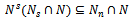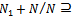
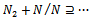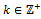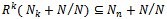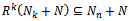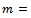
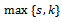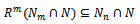for all n. Now is a descending chain of submodules of M/ N and M/ N is left quasi-Artinian, therefore there exists such that for all n. That is for all n. Now let Then and 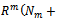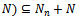for all n.

Now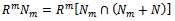

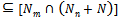and by modular law,

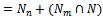for all n.

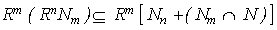Therefore

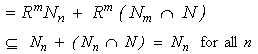Hence 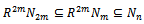for all n . Therefore M is left quasi-Artinian.

An immediate consequence of Propostion1.4, we have the following

Corollary

Let Т be the class of quasi-Artinian modules.If M = A+B where A,B in Т then

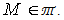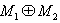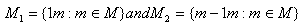Remark: Suppose that R has 1,so M= where

.Here 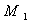is unitary and left quasi-Artinian if and only if 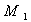is left So M . 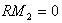quasi-Artinian if and only if 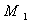is left Artinian .And M is left are Artinian. Artinian if and only if 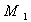and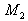

2. The Submodule Structures

In this section we study the submodules structure by consider modules over left quasi-Artinian ring. First we prove the following

Theorem2.1

Let R be a left quasi-Artinian ring. Then every finitely generated left

R-module is left quasi-Artinian

Proof:

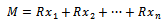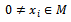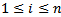Let M be a finitely generated left R-module, then where , . If 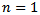then M is cyclic and therefore isomorphic to 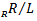where

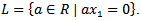. Since 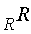is left quasi-Artinian, so is every factor module. Assume inductively that the Theorem holds for modules which can be generated by n-1 or fewer elements. Then 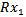is left quasi-Artinian and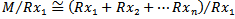

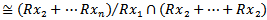which is left quasi-Artinian. Therefore M is left quasi-Artinian.

Let R be a ring and M is a left R –module. Then

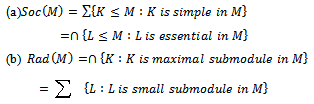Theorem2.2

Let R be a left quasi-Artinian ring and M is a left R-module .Then

(a) socM ess M

(b)RadMsmallinM

Proof:

(a) Let 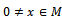. Then 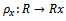such that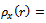 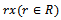is a homomorphism of R onto the submodule Rx with

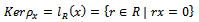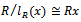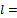
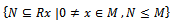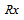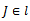Kernel . So . But R is left quasi-Artinian, hence by Proposition 1.4, Rx is left quasi-Artinian. We claim that Rx contains a minimal submodule. To prove this let be a nonempty collection of R-submodule of and Then 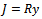for some 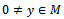.But 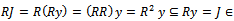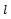. But l has a minimal element, hence 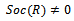.But 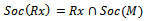, hence .

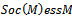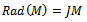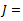
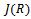(b) First we show that where . Since for any left R-module M the factor module 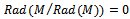. Therefore

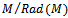is subdirect product of simple left R- modules. But since 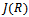is annihilates all simple left R-modules, so it annihilate 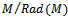that is .

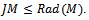Conversely since 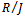is semi-simple then we have 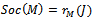Therefore 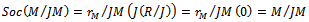. Hence

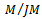is semi-simple 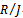-module. Since 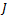is contained in annihilator of every simple R-submodule of M, then 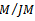is semi-simple R-module, thus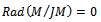 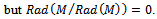. Therefore

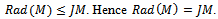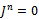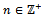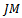
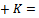
Now since R left quasi-Artinian, assume for some and consider an R-submodule K of M with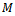. Multiplying with 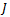we obtain 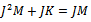, then 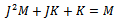. Continue in this way

we have after n steps, 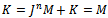. Hence 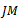small in M therefore by first part, 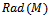small in M .

Corollary2.3

Let R be left quasi-Artinian ring and M left R-module, then M is finitely generated if and only if 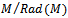is finitely generated.

Proof:

By Theorem 2.2, since 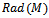small in M, then the result follows.

By the nil radical N=N(R) of a ring R we mean the sum of all nilpotent ideals of R, which is a nil ideal. It is well known [7. P.28 Theorem 2], that N is the sum of all nilpotent left ideals of R and it is the sum of all nilpotent right ideals of R.

Now we give another characterization of left quasi-Artinian ring ,namely the following:

Theorem2.4

Let R be a ring ,N = N(R) be the nil radical of R, then R is a left quasi-N is nilpotent and each of 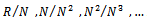Artinian if and only if is left quasi-Artinian R-modules.

Proof:

Suppose R is left quasi-Artinian. Then by[3,Corollary 2.3]N is nilpotent. Now let 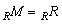. Then M is left quasi-Artinian R-module and 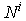is an ideal of R for all i. Therefore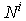is an R-submodule of M for all i.But by Proposition1.4, 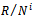is left quasi-Artinian for all 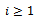. Also 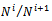is R-submodule of 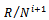so each 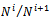is left quasi-Artinian.

To prove the converse, note that since 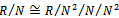it follows from Proposition 1.4, that 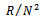is left quasi-Artinian R-module and by induction 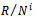is left quasi-Artinian for all i. But N is nilpotent, hence there exists 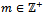such that 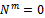, therefore 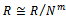is left quasi-Artinian R-module. Hence R is left quasi-Artinian ring.

3. The Ideal Structures

In this section we study the ideal structures in a left quasi-Artinianring. Note that if R= 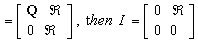is a nilpotent ideal of R. There I and 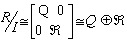are left quasi-Artinian, but R is not left quasi-Artinian. Hence the class of left quasi-Artinian rings is not E-closed, however we have the following:

Theorem3.1

A finite direct sum of left quasi-Artinian rings is a left quasi-Artinian.

Proof:

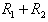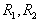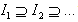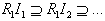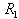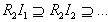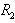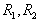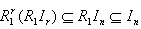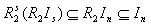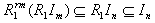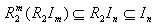By induction, it is enough to prove the result when R=where are left quasi-Artinian. Let be a descending chain of left ideals of R.Thenis a descending chain of left ideals of and is a descending chain of left ideals of ,but are left quasi-Artinian rings,hence there exist r,s such thatand.Let m=max{r,s}.Then and for all n. But 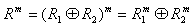,hence 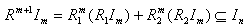for all n and 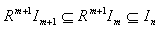for all n.Therefore R is left quasi-Artinian.

Theorem3.2

Let I be a non-nilpotent left ideal in a left quasi-Artinian ring, then I contains a non-zero idempotent element .

To prove this we need the following lemma.

Lemma3.3

Let R be a left quasi-Artinian ring. Then every non-nilpotent left ideal of R contains a minimal non-nilpotent left ideal.

Proof:

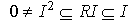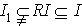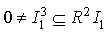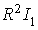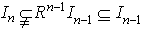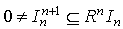Let I be a non-nilpotent left ideal of R and suppose that I does not contains a minimal non-nilpotent left ideal of R. Then and RI is not nilpotent. Therefore there exists a non-nilpotent left ideal. Hence and is not nilpotent. In this way we can find a non-nilpotent left ideal then and 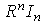is not nilpotent and so on. Hence 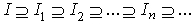is an infinite descending chain of left ideals of R which is a contradiction. Therefore I contains a minimal non-nilpotent left ideal of R.

Proof of Theorem

Let I be non-zero non-nilpotent left ideal of R. Since R is a left quasi-Artinian ring, then by Lemma3.3, I contains a minimal non-nilpotent left ideal K. Since 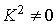then there exists 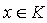such that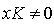. However 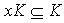and xK is a left ideal of R, hence by minimilty of K we have xK =K . Therefore there exists 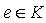such that 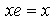and since 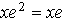we get that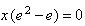. Now, let 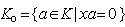, therefore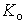is a left ideal of R and 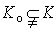since, 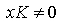, for all 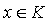. Therefore we must have 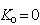and 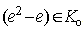. Hence 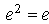. Since 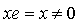we have that 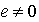. Now, 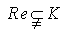is a left ideal of R and contains 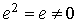, so that 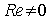, then 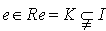. Hence .

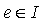Corollary3.4

If R is left quasi-Artinian ring, then every nil left ideal of R is nilpotent .

Proof:

Let N be a non-zero nil left ideal of R and suppose that N is not nilpotent. Then by Theorem 3.2, there exists a nonzero idempotent element e and eN. Therefore e is nilpotent which is a contradiction. Hence N must be nilpotent.

Next we prove the following

Theorem3.5

Let R be a semi-prime left quasi-Artinian ring and I be a nonzero

left ideal of R, then I = Re for some nonzero idempotent e in R.

Proof:

Since I is not nilpotent, it follows from Theorem 3.2,that I contains a non-zero idempotent element say, e. Let 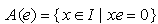then the set of left ideals 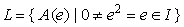is not empty. Now, if A(e) 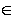L, then RA(e) 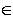L. Now since I is a left ideal of R, then re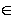I , where r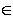R , e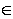I , therefore 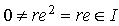, but R is a left quasi-Artinian, hence by Theorem1.2, L has a minimal element 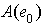, say. Eithe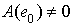r or 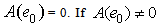, then 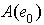must have an idempotent 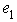, say. By definition of 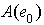, 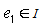and . 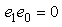Consider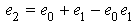, then 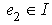and is itself a non-zero idempotent element. Moreover, 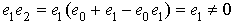, hence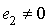. Now if 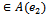, then 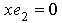and 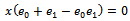. Therefore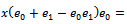 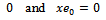. Therefore 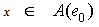and 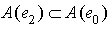, since 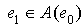and 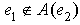we have that 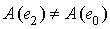, which contradicts the minimality of 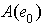. Therefore 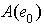=0 . 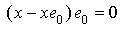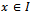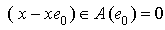But for all hence and 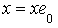for all xI , which implies that 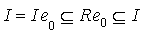. Hence.

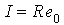Corollary3.6

Any semi-prime left quasi-Artinian ring is a semi-simple left Artinian.

Proof:

By Theorem 3.5 every non-zero left ideal of R is generated by a non-zero idempotent e, say. But we know that e acts as right identity for the left ideal I =Re, and since R is itself an ideal, hence R has an identity element. Therefore R is left Artinian. Now, J(R) is nilpotent, and R is a semi-prime ring, implies that J(R) = 0. Hence R is a semi-simple.

Now we describe left quasi-Artinian rings using the non commutative version of Wedderburn Theorem. Inparticular we prove the following

Theorem3.7

A commutative ring R is quasi-Artinian if and only if R is a direct sum of an Artinian ring with identity and a nilpotent ring.

To prove this we need the following

Lemma3.8

Let R be a left quasi-Artinian ring and N be the nil radical of R. Then 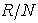is a semi-simple Artinian ring.

Proof:

Since N is nilpotent and 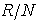is left quasi-Artinian, it follows that 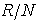is a semi-prime left quasi-Artinian. Therefore by Corollary 3.5,

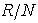is a semi-simple Artinian ring.

Proof of theorem3.7

Suppose that R is a direct sum of an Artinian ring with identity and a nilpotent ring, since any Artinian ring and any nilpotent ring are quasi-Artinian ,it follows that R is a quasi Artinian ring.

To prove the converse. Let N = N(R) be a nil radical of R. Then by

Corollary 3.4,N is nilpotent and by Lemma 3.8, 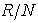is a semi-simple Artinian ring. Therefore by Wedderburn's Theorem 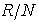is a finite direct sum of its minimal ideals, each of which is a simple Artinian ring, that is

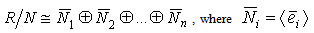is a minimal ideal of

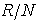which is a simple Artinian ring . But a finite direct sum of Artinian is again Artinian, hence 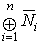is an Artinian ring and 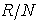is a semi-simple Artinian. But 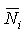is a semi-simple Artinian so, it has an identity element. Therefore 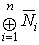is an Artinian ring with identity. Hence, 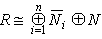and R is a direct sum of Artinian ring with identity and nilpotent ring .

Finally we prove the following which characterizes the prime ideals in left Quasi-Artinian rings.

Theorem3.8

Let R be a commutative quasi-Artinian ring and I be a minimal ideal in R. Then ann( I ) is a maximal ideal .

To prove this we need the following

Lemma3.9

If R is a commutative quasi-Artinian ring ,then every prime ideal of R is maximal .

Proof:

Let P be a prime ideal of R, then 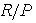is a prime ring. Now 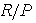is a semi-prime quasi-Artinian ring. Therefore by Corollary 3.5 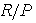is a semi-simple Artinian .Hence by Wedderburn's Theorem 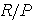is a finite direct sum of minimal ideals, each of which is a simple Artinian ring. But a prime ring cannot be written as a direct sum of non-trivial ideals, hence 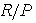is a simple ring. Therefore P is maximal.

An immediate consequence of Lemma 3.9 we have the following

Corollary3.10

If R is a quasi-Artinian ring, then J(R)= rad(R)= N(R). Where J(R) is the Jacobson radical of R and rad(R ) isthe prime radical of R.

Proof of Theorem3.8

By Lemma 3.10, it enough to show that ann( I ) is a prime ideal in R.

Let 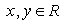such that 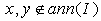. Then 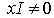and 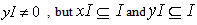. But I is a minimal ideal of R , hence 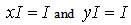. Therefore 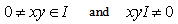. Hence 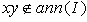, and ann( I ) is a prime ideal of R .