1. Introduction

The concept of fuzzy sets and fuzzy set operations was first introduced by Zadeh[9]. Accordingly, fuzzy topological spaces were introduced by Chang[4]. Several researches were the generalizations of the notion of fuzzy set. The idea of intuitionistic fuzzy set (IFS, for short) was first published by Atanassov[1, 2, 3]. Subsequently, Tapas et al.[8] defined the notion of generalized intuitionistic fuzzy set and studied the basic concept of generalized intuitionistic fuzzy topology. Our aim in this paper is to extend those ideas of general topology in generalized intuitionistic fuzzy topological space (GIFTS, in short). In section 3, we define generalized intuitionistic fuzzy ideal for a set. Here we generalize the concept of intuitionistic fuzzy ideal topological concepts, first initiated by Salama et al.[6] in the case of generalized intuitionistic fuzzy sets. In section 4, we introduce the notion of the generalized intuitionistic fuzzy local function corresponding to GIFTS. Recently we have deduced some characterization theorems for such concepts exactly analogous to general topology and succeeded in finding out the generated new generalized intuitionistic fuzzy topologies for any GIFTS.

2. Preliminaries

Deifintion.2.1.[6] A nonempty collection of intuitionistic fuzzy sets 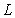of a set X is called intuitionistic fuzzy ideal on X iff i) 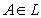and B ⊆ A ⇒ 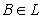(heredity), (ii) 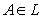and 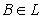⇒ A ⊦ B∈L (finite additivity).

We shall present the fundamental definitions given by Tapas:

Definition 2.2.[8]. Let X is a nonempty fixed set. An generalized intuitionistic fuzzy set (IFS for short) A is an object having the form 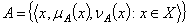where the function 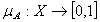and 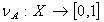denote the degree of membership(namely 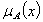) and the degree of non membership(namely 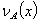) of each element 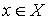to the set A, respectively, and 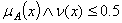for all .

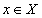Remark. 2.1. For the sake of simplicity, we shall use the symbol 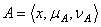for the GIFS.

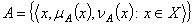Definition2.3.[8]. 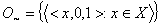and 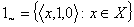are empty and universal generalized inuitionistic fuzzy sets

Definition 2.4.[8]. A generalized intuitionistic fuzzy topology (GIFT for short) on a nonempty set X is a family 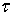of GIFSs in X satisfying the axioms in[8].

3. Basic Properties of Generalized Intuitionistic Fuzzy Ideals

Definition 3.1. Let X is non-empty set and L a family of GIFSs. We will call L is a generalized intuitionistic fuzzy ideal (GIFL for short) on X if

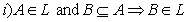[heredity],

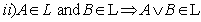[Finite additivity].

A generalized intuitionistic Fuzzy Ideal L is called a 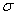- generalized intuitionistic fuzzy ideal if 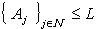, implies 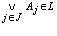(countable additivity).

The smallest and largest generalized intuitionistic fuzzy ideals on a non -empty set X are 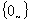and GIFSs on X. Also, 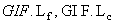are denoting the generalized intuitionistic fuzzy ideals (GIFLS for short) of fuzzy subsets having finite and countable support of X respectively. Moreover, if A is a nonempty GIFS in X, then 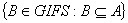is an GIFL on X. This is called the principal GIFL of all IFSs of denoted by GIFL.

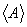Remark 3.1.

i) If 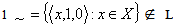, then L is called generalized intuitionistic fuzzy proper ideal.

ii) If , then L is called generalized intuitionistic fuzzy improper ideal.

iii) .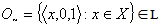

Example.3.1. Let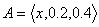, , 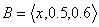and 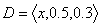, then the family 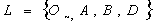of GIFSs is an GIFL on X.

Example.3.3. Let 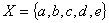and 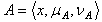given by :

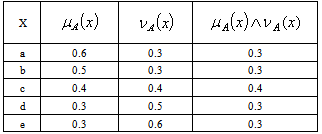Then the family GIF 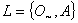is an GIFL on X.

Definition 3.2. Let L₁ and L₂ be two GIFLs on X. Then L₂ is said to be finer than L₁ or L₁ is coarser than L₂ if L₁ ≤ L₂. If also L₁ ≠ L₂. Then L₂ is said to be strictly finer than L₁ or L₁ is strictly coarser than L₂.

Two GIFLs said to be comparable, if one is finer than the other. The set of all GIFLs on X is ordered by the relation L₁ is coarser than L₂ this relation is induced the inclusion in IFSs.

The next Proposition is considered as one of the useful result in this sequel, whose proof is clear.

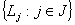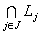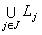Proposition 3.1. Let be any non - empty family of generalized intuitionistic fuzzy ideals on a set X. Then and are generalized intuitionistic fuzzy ideal on X, where 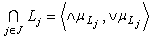and .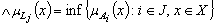

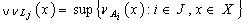In fact L is the smallest upper bound of the set of the L_j in the ordered set of all generalized intuitionistic fuzzy ideals on X.

Remark3.2. The generalized intuitionistic fuzzy ideal by the single generalized intuitionistic fuzzy set 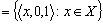is the smallest element of the ordered set of all generalized intuitionistic fuzzy ideals on X.

Proposition.3.3 A GIFS A in generalized intuitionistic fuzzy ideal L on X is a base of L iff every member of L contained in A.

Proof.(Necessity) Suppose A is a base of L. Then clearly every member of L contained in A.

(Sufficiency) Suppose the necessary condition holds. Then the set of generalized intuitionistic fuzzy subset in X contained in A coincides with L by the Definition 3.1.

Proposition.3.4. For a generalized intuitionistic fuzzy ideal L₁ with base A, is finer than a fuzzy ideal L₂ with base B iff every member of B contained in A.

Proof. Immediate consequence of Definitions

Corollary.3.1. Two generalized intuitionistic fuzzy ideals bases A, B, on X are equivalent iff every member of A, contained in B and via versa.

Theorem.3.1. Let η = {μ_j : j ∈ J} be a non empty collection of generalized intuitionistic fuzzy subsets of X. Then there exists a generalized intuitionistic fuzzy ideal

L (η) = {A ∈ IFSs : A ⊆ ⊦ A_j} on X for some finite collection {A_j : j = 1,2, ......, n ⊆ η}.

Proof : Clear.

Remark.3.3

ii) The generalized intuitionistic fuzzy ideal L (η) defined above is said to be generated by η and η is called subbase of L(η).

Corollary.3.2. Let L₁ be an generalized intuitionistic fuzzy ideal on X and A ∈ IFSs, then there is a generalized intuitionistic fuzzy ideal L₂ which is finer than L₁ and such that A ∈ L₂ iff A ⊦ B ∈ L₂ for each B∈ L₁.

Theorem.3.2. If an GIFS 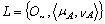is an generalized intuitionistic fuzzy ideal on X, then so is 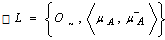is an generalized intuitionistic fuzzy ideal on X.

Proof. Clear

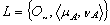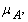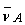Theorem.3.3. A GIFS is a generalized intuitionistic fuzzy ideal on X iff the intuitionistic fuzzy sets and are generalized intuitionistic fuzzy ideals on X.

Proof. Let 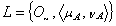be an GIFL of X, 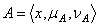, Ten clearly 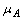is a fuzzy ideal on X. Then 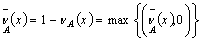= 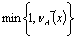if 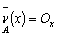. Then is the smallest generalized intuitionistic fuzzy ideal , Or 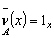then is the largest generalized intuitionistic fuzzy ideal on X.

Corollary.3.3. A GIFS is an generalized intuitionistic fuzzy ideal on X iff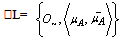

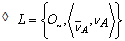and are generalized intuitionistic fuzzy ideals on X.

Proof. Clear from the definition 3.1.

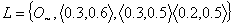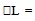
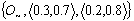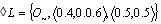Example.3.4. Let X a non empty set and GIFL on X given by: .Then and . and .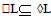

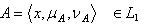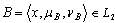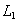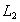Theorem.3.4. Let and , where and are generalized intuitionistic fuzzy ideals on the set X. then the generalized intuitionistic fuzzy set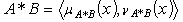 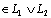on X. a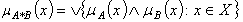nd , and.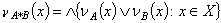

Definition.3.4 For a GIFTS (X, τ), A ∈ GIFSs. Then A is called

i) Generalized intuitionistic fuzzy dense if cl (A) =.

ii) Generalized intuitionistic fuzzy nowhere dense subset if Int (cl(A))= .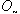

iii) Generalized intuitionistic fuzzy codense subset if

Int (A) =.

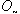v) Generalized intuitionistic fuzzy countable subset if it is a finite or has the some cardinal number.

iv) Generalized intuitionistic fuzzy meager set if it is a generalized intuitionistic fuzzy countable union of generalized intuitionistic fuzzy nowhere dense sets.

The following important Examples of generalized intuitionistic fuzzy ideals on GIFTS (X. τ).

Example.3.5. For a GIFTS (X, τ) and L_n = {A ∈GIFSs : Int (cl(A)) = 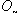is the collection of generalized intuitionistic fuzzy nowhere dense subsets of X. It is a simple task to show that L_n is generalized intuitionistic fuzzy ideal on X.

Example.3.6 For a IFTS (X, τ) and L_m = {A ∈ IFSs: A is a countable union of generalized intuitionistic fuzzy nowhere dense sets} the collection of generalized intuitionistic fuzzy meager sets on X. one can deduce that L_m is generalized intuitionistic fuzzy σ - ideal on X.

Example.3.7. For a IFTS (X, τ) with generalized intuitionistic fuzzy ideal L. then

< L ∩ τ^c > = {A ∈ IFSs : there exists B ∈ L ∩ τ^c such that A ⊆ B} is a generalized intuitionistic fuzzy ideal on X.

Example.3.8. Let f: (X, τ ₁) (Y, τ₂) be a function, and L, J are two generalized intuitionistic fuzzy ideals on X and Y respectively. Then

i) f (L) = {f (A): A ∈ L} is an generalized intuitionistic fuzzy ideal.

ii) If f is injection. Then f ^-1 (J) is generalized intuitionistic fuzzy ideal on X.

4. Generalized Intuitionistic Fuzzy local Functions and *-GIFTS

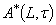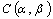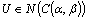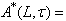
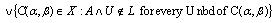
Definition.4.1. Let (X, τ) be an generalized intuitionistic fuzzy topological spaces (GIFTS for short ) and L be generalized intuitionistic fuzzy ideal (GIFL, for short) on X. Let A be any GIFS of X. Then the generalized intuitionistic fuzzy local function of A is the union of all generalized intuitionistic fuzzy points ( IFP, for short) such that if and 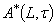is called an generalized intuitionistic fuzzy local function of A with respect to 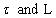which it will be denoted by 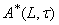, or simply .

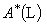Example .4.1. One may easily verify that.

If L=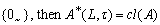, for any generalized intuitionistic fuzzy set 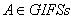on X.

If 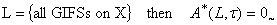, for any 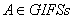on X .

Theorem.4.1. Let 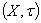be a GIFTS and 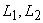be two generalized intuitionistic fuzzy ideals on X. Then for any generalized intuitionistic fuzzy sets A, 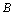of X. then the following statements are verified

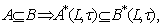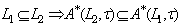i)

ii) .

iii) .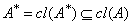

iv) .

v) .,

vi)

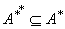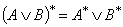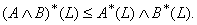vii)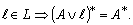

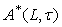is generalized intuitionistic fuzzy closed set .

Proof.

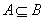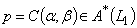i) Since, let then 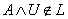for every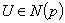. By hypothesis we get 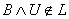, then .

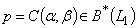ii) Clearly. 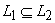implies 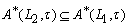as there may be other IFSs which belong to 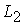so that for GIFP 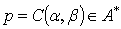but 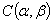may not be contained in .

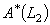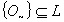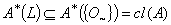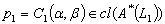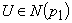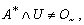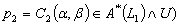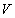
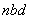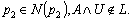iii) Since for any GIFL on X, therefore by (ii) and Example 4.1, for any GIFS A on X. Suppose. So for every , there exists such that for every of Since 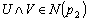then 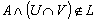which leads to 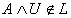, for every 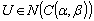therefore 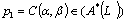and so 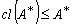While, the other inclusion follows directly. Hence 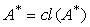. But the inequality .

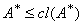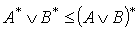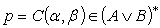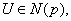
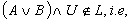
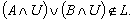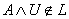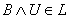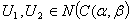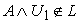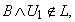
iv) The inclusion follows directly by (i). To show the other implication, let then for every then, we have two cases and or the converse, this means that exist such that , 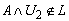and 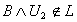. Then 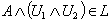and 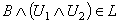this gives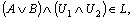 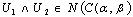which contradicts the hypothesis. Hence the equality holds in various cases.

vi) By (iii), we have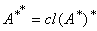

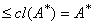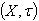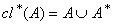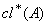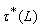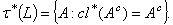Let be a GIFTS and L be GIFL on X . Let us define the generalized intuitionistic fuzzy closure operator for any GIFS A of X. Clearly, let is a generalized intuitionistic fuzzy operator. Let be GIFT generated by .i.e . Now 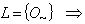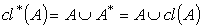for every generalized intuitionistic fuzzy set A. So, 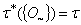. Again 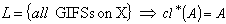, because 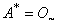, for every generalized intuitionistic fuzzy set A so 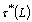is the generalized intuitionistic fuzzy discrete topology on X. So we can conclude by Theorem 4.1.(ii). 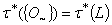i.e. 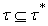, for any generalized intuitionistic fuzzy ideal 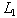on X. 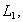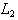In particular, we have for two generalized intuitionistic fuzzy ideals and on X, .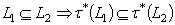

Theorem.4.2. Let 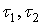be two generalized intuitionistic fuzzy topologies on X. Then for any generalized intuitionistic fuzzy ideal L on X, 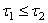implies

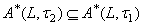, for every A .

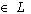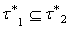Proof. Clear.

A basis 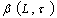for 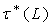can be described as follows: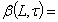

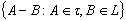Then we have the following theorem

Theorem 4.3.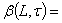 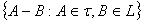Forms a basis for the generated GIFT of the GIFT 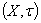with generalized intuitionistic fuzzy ideal L on X.

Proof. Straight forward.

The relationship between τ and 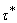(L) established throughout the following result which have an immediately proof .

Theorem 4.4. Let 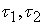be two generalized intuitionistic fuzzy topologies on X. Then for any generalized intuitionistic fuzzy ideal L on X, 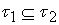implies .

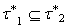Theorem 4.5 : Let 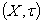be a GIFTS and 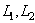be two generalized intuitionistic fuzzy ideals on X . Then for any generalized intuitionistic fuzzy set A in X, we have

i)

ii)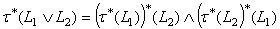

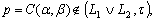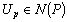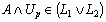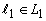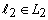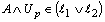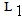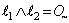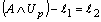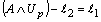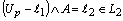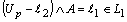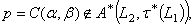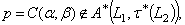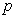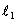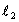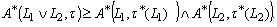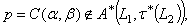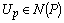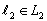Proof Let this means that there exists such that i.e. There exists and such that because of the heredity of , and assuming .Thus we have and therefore and . Hence or because must belong to either or but not to both. This gives .To show the second inclusion, let us assume. This implies that there exist and such that 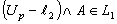. By the heredity of 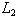, if we assume that 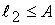and define 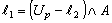. Then we have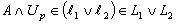. Thus, 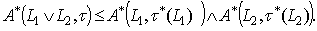and similarly, we can get 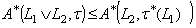. This gives the other inclusion, which complete the proof.

Corollary 4.1. Let 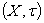be a GIFTS with generalized intuitionistic fuzzy ideal L on X. Then

i) .

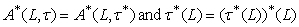ii)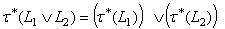

Proof. Follows by applying the previous statement.